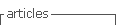1. INTRODUCCIÓN
La elección de velocidad depende de factores que se relacionan con: a) el conductor, b) el vehículo, c) la carretera, d) el entorno y e) la operación y control de la carretera (Sekhar, Nataraju, Velmurugan, Kumar, & Sitaramanjaneyulu, 2016). Su relación con estos factores han sido ampliamente estudiados en la literatura, por ejemplo, los rasgos de la personalidad pueden afectar la elección de velocidad (García-Ramírez, 2014), la edad del conductor (Keay et al., 2013; Thompson et al., 2012), la experiencia del conductor (Goralzik & Vollrath, 2017), sexo (Goralzik & Vollrath, 2017), entre otros. También, el vehículo también puede afectar la velocidad tales como el tipo (Dhamaniya & Chandra, 2013; Wang, 2006) o en año de fabricación del mismo (Gargoum, El-Basyouny, & Kim, 2016) o su longitud (Giles, 2004). Por otro lado, características de la carretera pueden influir sobre la elección de la velocidad, por ejemplo el número de carriles (Dinh & Kubota, 2013), ancho del carril (Bassani & Sacchi, 2012), la pendiente longitudinal (Ding, Zhao, Rong, & Ma, 2015), el estado del pavimento (Sekhar et al., 2016; Wang, 2006), el radio de la curva circular (Lamm, Psarianos, & Mailaender, 1999), la longitud de la entre-tangencia (Pérez, García, Camacho, & D’Attoma, 2010), entre otros. Así mismo, el entorno en donde está la carretera también puede condicionar la velocidad, por ejemplo, la densidad de objetos en zonas laterales de la carretera (Antonson, Ahlström, Mårdh, Blomqvist, & Wiklund, 2014; Wang, 2006), uso de la tierra (Gargoum et al., 2016; Giles, 2004), cambios de luminosidad (Bassani, Catani, Cirillo, & Mutani, 2016) o diversas condiciones climáticas (Rahman & Lownes, 2012), entre otros. Finalmente, la operación del tránsito y su control, como los límites de velocidad (Goralzik & Vollrath, 2017), cámaras de velocidad (Schechtman, Bar-Gera, & Musicant, 2016) o presencia de fotoradares (Cheng et al., 2005) también pueden afectar la elección de velocidad. En resumen existen muchos factores que pueden influir sobre la elección de velocidad por lo que ha sido difícil obtener resultados concluyentes; es así que, las investigaciones se han centrado en unos pocos factores y han mantenido el resto como constantes, por ejemplo, analizar los factores de la carretera manteniendo constante el tipo de vehículo, las condiciones climáticas o de luminosidad, la topografía del terreno adyacente, el estado del pavimento, etc.
Desde el punto de vista del diseño, interesa conocer la relación entre la velocidad del vehículo (operación o diseño) con los parámetros geométricos de la carretera (curvas, entre-tangencias, etc.). Si se conoce esta relación se podrá predecir las velocidades en esos elementos, con sólo conocer la geometría de la carretera. Con esta predicción de velocidades se pueden realizar los análisis de consistencia del diseño con el fin de que la geometría no permita cambios bruscos de velocidades entre elementos, los cuales pueden ser peligrosos al no estar acorde a las expectativas del conductor, es decir, con esto se podrá reducir la probabilidad de accidentes de tránsito en una carretera.
Dada la importancia de conocer la velocidad del vehículo durante la fase del proyecto de la carretera, es decir, antes de que se construya, varias investigaciones se han llevado a cabo para tratar de obtenerlas. Para ello se han recolectado velocidades in situ con diversos equipos y luego se han relacionado estadísticamente con las características de la carretera. En general, esta relación se ha llevado a cabo con análisis de regresión (García-Ramírez, 2014). Normalmente, la velocidad que se ha usado en las calibraciones a nivel mundial es la de operación o percentil 85 de la velocidad, con la que el 85% de los conductores elegirán una velocidad igual o menor que ese valor. Para el cálculo de esta velocidad, el vehículo debe viajar en flujo libre, es decir, que no exista elemento geométrico o tránsito vehicular que impida la elección libre de la velocidad. Aunque se hayan calibrado ecuaciones entre la velocidad de operación entre elementos relacionados a la curva horizontal y a la entre-tangencia horizontal, aún no está clara como la pendiente longitudinal influye sobre la velocidad del vehículo, lo cual es más crítico en carreteras de montaña.
En ese escenario, esta investigación tuvo por objetivo calibrar ecuaciones de velocidad de operación en carreteras rurales montañosas de dos carriles, en donde se analice la influencia de la curva horizontal, la entre-tangencia horizontal y la pendiente longitudinal de la carretera. Se eligió una carretera de dos carriles, dado que es en ellas en donde la relación velocidad –geometría es más evidente (Lamm et al., 1999). Esta investigación, además de su aporte al entendimiento de la influencia de la pendiente longitudinal sobre la velocidad de operación, también ofrece las primeras ecuaciones aplicables en un contexto ecuatoriano.
El resto del artículo se organiza de la siguiente manera: la sección 2 muestra los métodos utilizados en esta investigación, detallando el tamaño de muestra, la ruta de medición, el equipo de medición, los conductores y vehículos participantes, para luego explicar el proceso de recolección y procesamiento de datos. Posteriormente, en la sección 3, de resultados y discusión, se muestran los modelos calibrados y luego su validación, en donde paralelamente se los compara con los resultados previos obtenidos en la literatura. Y finalmente, se exponen las principales conclusiones del trabajo.
2. MATERIALES Y MÉTODOS
2.1 Tamaño de la muestra
El tamaño de la muestra se calculó con la ecuación propuesta por Pignataro (Pignataro, 1973). Para esa ecuación se asumió un error estándar de 8 km/h (Paladines, 2016; Torres, 2016; Verdesoto, 2016) y un error de 5 km/h, el cual es menor que el utilizado al umbral más bajo de los análisis de consistencia (10 km/h):
Donde:
n: tamaño de muestra, K: constante en función del nivel de confianza elegido,σ: desviación estándar, U: desviación normal correspondiente al percentil de velocidad, el: precisión o error admisible.
Con un nivel de confianza del 95% (K = 1,96) y un valor de U=1,04 (para la velocidad de operación), se calculó un tamaño muestral de 16 recorridos.
2.2 Carretera de medición
La carretera de prueba cumplió con los siguientes criterios: a) es una carretera rural de dos carriles, b) es una carretera que atraviesa por una topografía montañosa, c) posee pendientes longitudinales menores a 10%, d) tuvo pavimento en buen estado y e) permitió la circulación vehicular en flujo libre. La carretera de prueba fue la que une la vía Loja hacia Catamayo (Ver figura 1), la cual tiene una longitud aproximada de 32 km, un ancho de carril de 3,2 m y ancho de espaldón de 1,5 m. Esta vía posee 207 curvas horizontales entre 45-430 m de radio y pendientes longitudinales entre -10 a 10%.
La geometría de la carretera fue obtenida de los planos originales del estudio de la vía y de un estudio de ampliación a 4 carriles (MTOP & Asociación del Sur, 2015). Estos planos fueron comparados con las imágenes satelitales de Google Maps (Google Inc., 2018). Cuando existían diferencias entre estas dos fuentes, se trazó un nuevo alineamiento horizontal en ese tramo usando AutoCAD Civil 3D (Autodesk, 2016) y el alineamiento generado por las coordenadas del equipo de medición.
2.3 Equipo de medición
El equipo de medición utilizado fue el equipo Video VBOX Lite, que ya fue empleado previamente en otras investigaciones con medición de velocidades (por ejemplo Memon, Khaskheli, & Qureshi, 2008). Este equipo graba el recorrido de un vehículo en donde se instale cada 0,1 s. Esta grabación incluye un video (dado que tiene una cámara de alta resolución), coordenadas, alturas, velocidades, entre otros. Cada punto está georreferenciado gracias a la antena GPS que tiene el equipo. La precisión de la velocidad es de 0,2 km/h, mientras que en las coordenadas es de 0,05% de la distancia recorrida y en las alturas es de ± 10 m.
2.4 Conductores y vehículos participantes
Para esta investigación, los conductores debían cumplir con ciertos requisitos: a) poseer licencia de conducción vigente, b) disponer de un vehículo liviano propio, c) haber recorrido la ruta previamente y d) haber conducido frecuentemente en los últimos dos meses. Se eligieron 16 conductores para realizar los 16 recorridos necesarios del tamaño muestral. De estos conductores, la distribución fue 50/50 entre el sexo masculino y femenino, dado que en Ecuador aproximadamente tiene esa tendencia (INEC, 2010). Los conductores tuvieron una edad promedio de 40 años (25-62), experiencia de conducción promedio de 15 años (5-37), puntos disponibles en la licencia de conducir promedio de 29/30 (19,5-30). Por otro lado, en lo que respecta los vehículos de los participantes, éstos tuvieron un cilindraje promedio de 2,3 cc (1,3-4,6), un año de fabricación promedio 2009 (2004-2017) y su última revisión mecánica promedio fue de 1,2 meses (1-3) antes del día de la recolección de datos. En estos vehículos se instaló el Video VBOX Lite para la recolección de datos.
2.5 Recolección y procesamiento de datos de velocidad
El equipo Video VBOX Lite se instaló en cada vehículo liviano con la precaución de no interferir con las actividades de conducción. La antena GPS del equipo fue colocada en el techo del vehículo para evitar interferencia de la estructura del vehículo y pueda registra el mayor número de satélites (máximo 8). La cámara fue colocada en la parte izquierda del parabrisas delantero apuntando hacia la carretera. La cámara y la antena GPS fue conectado al data logger del equipo, el cual fue colocada discretamente debajo del asiento delantero. Durante la instalación, se le recordó al conductor los fines académicos del registro y se lo o la motivaba a conducir como lo hace de manera habitual. Los datos fueron recolectados durante buenas condiciones climáticas, con clima seco y durante la luz del día. La recolección de datos empezó en la ciudad de Loja, llegaba a la ciudad de Catamayo y retornaba a la ciudad de Loja. Una ver que se terminó con el recorrido, se retiraba el equipo y el conductor debía responder algunas preguntas personales y de su vehículo.
Luego de la recolección de datos, se exportaron las velocidades, posiciones y alturas en un intervalo de 1 s y se conformó la primera base de datos. En cada recorrido, se eliminaron tramos del inicio y final para evitar la inclusión del tránsito urbano y la posible interferencia al conductor, con lo que se conformó una nueva base de datos. En esta base de datos, de 27 km, se eliminaron los tramos en los cuales el vehículo no estaba en flujo libre, por ejemplo, cuando el vehículo estaba en seguimiento o que realizando una maniobra de adelantamiento. Especialmente, en esta última se verificó que no haya inconsistencias entre los recorridos, ya que en una maniobra de adelantamiento, el recorrido del vehículo es mayor que cuando no se adelanta. En esa nueva base de datos se calculó en cada recorrido: Loja-Catamayo (ver figura 2) y Catamayo-Loja (ver figura 3), la velocidad de operación.
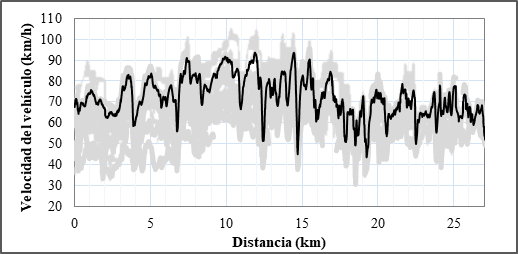
Figura 2. Perfiles de velocidades de los recorridos Loja-Catamayo en donde se ha sombreado el perfil de velocidad de operación calculado.
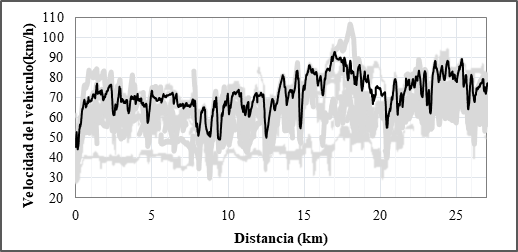
Figura 3. Perfiles de velocidades de los recorridos Catamayo-Loja en donde se ha sombreado el perfil de velocidad de operación calculado.
Finalmente, a partir del perfil de velocidad de operación calculado se obtuvo las velocidades de operación en el centro de las curvas circulares y en el centro de las entre-tangencias horizontales, con el fin de relacionarlas con los parámetros geométricos de la carretera.
3. RESULTADOS Y DISCUSIÓN
Se trató de encontrar relación estadística, mediante análisis de regresión, entre la velocidad de operación en el centro de las curvas y entre-tangencias horizontales con algunos parámetros geométricos de la carretera, del conductor y del vehículo. Los parámetros evaluados de la carretera fueron: radio de la curva horizontal, longitud de la curva horizontal, pendiente longitudinal, longitud de la recta, mientras que los relacionados con el conductor fueron: su edad, su experiencia y su sexo, y los relacionados con el vehículo fueron: el cilindraje, año de fabricación y periodo de mantenimiento.
De todas las variables analizadas, las que mostraron tendencias estadísticamente significativas fueron: el radio de la curva horizontal y pendiente longitudinal para las curvas horizontales, y la longitud de la entre-tangencia y pendiente longitudinal en las entre-tangencias horizontales. Todos los análisis de regresión se realizaron empleando el programa estadístico Minitab 14.2 (State College, 2005). Cada calibración de datos era realizada si por lo menos existían 19 datos. El ajuste de regresión era aceptado cuando el coeficiente determinación (R2) era mayor a 0,40 para las curvas y 0,25 para las entre-tangencias. Se utilizaron esos valores dado que en la literatura se encontraron que estos coeficiente en curvas eran mayores que los de las entre-tangencias (Pérez, 2012).
Luego de la calibración de las ecuaciones se procedió a realizar su validación mediante los análisis de los errores, la prueba chi-cuadrado y la prueba t de Student.
3.1 Calibración de las ecuaciones
Se realizó la calibración de ecuaciones para las curvas horizontales y luego para las entre-tangencias horizontales. En el primer caso, se trató de obtener una ecuación general para todas las pendientes longitudinales, sin embargo, luego de obtener un R2 menor a 0,4, se segmentaron las pendientes utilizando el análisis de Tukey con el Minitab 14.2 (State College, 2005), con el cual se determinaron los rangos de pendientes en los cuales eran estadísticamente diferentes de otros. Se ajustaron estos valores para que se tengan similares rangos tanto en las pendientes positivas como en las negativas. Los valores de pendientes entre -3,99 a 0% y 0 a 3,99% son coherentes con las que se obtuvieron en otras investigaciones (Fitzpatrick et al., 2000). Finalmente, las ecuaciones calibradas para las curvas horizontales se muestran en la tabla 1.
Tabla 1. Ecuaciones calibradas de predicción de la velocidad de operación en curvas circulares horizontales
| G (%) | Ecuación de predicción | R² | Rango de radios (m) | N° |
| 6 a 10 % | Vc85 = 74,95-794,59/R | 0,40 | 45 a 400 | (2) |
| 4 a 5,99% | Vc85 = 78,33-740,66/R | 0,48 | 50 a 300 | (3) |
| 0 a 3,99% | Vc85 = 91,42-2039,59/R | 0,67 | 80 a 400 | (4) |
| -3,99 a 0% | Vc85 = 94,59-2366,42/R | 0,85 | 80 a 400 | (5) |
| -5,99 a -4% | Vc85 = 86,44-1433,64/R | 0,78 | 50 a 300 | (6) |
| -10 a -6% | Vc85 = 81,10-1304,97/R | 0,45 | 45 a 430 | (7) |
| Vc85 = Velocidad de operación en curvas circulares horizontales en km/h, G = pendiente longitudinal de la carretera, R = radio de la curva circular horizontal, R2 = coeficiente de determinación, N° = número de ecuación. | ||||
Utilizando las ecuaciones de la tabla 1, por ejemplo para una curva de radio 50 m, las velocidades de operación en el centro de la curva serían: 59,1 km/h (6 a 10%), 63,5 km/h (4 a 5,99%), 50,6 km/h (0 a 3,99%), 47,3 km/h (-3,99 a 0%), 57,8 km/h (-5,99 a -4%), 57,8 km/h (-10 a -6%). El valor más alto de velocidad está entre 3,99 a 5,99%, luego desciende con el aumento de la pendiente, lo cual está tiene sentido, dado que las altas pendientes llevan a una reducción mayor de la velocidad. Por otra parte, los valores más bajos se encuentran entre las pendientes -3,99 a +3,99% y luego aumenta con el descenso de la pendiente (-5,99 a -4%), lo cual también tiene sentido dado que las pendientes descendentes favorecen el movimiento del vehículo, sin embargo, en pendientes negativas más bajas (-10 a -6%) existe una reducción de esa velocidad, lo cual está relacionado con la percepción del riesgo del conductor, por lo que al notar que el vehículo sigue ganando velocidad, éste tiende a reducirla.
En el caso de que se utilice las ecuaciones de la tabla 1 para radios de curva mayores, como por ejemplo, para 400 m, las velocidades de operación serían: 73,0 km/h (6 a 10%), 76,5 km/h (4 a 5,99%), 86,3 km/h (0 a 3,99%), 88,7 km/h (-3,99 a 0%), 82,9 km/h (-5,99 a -4%), 77,8 km/h (-10 a -6%). En este caso, los valores más altos de velocidades se encuentran entre las pendientes -3,99 a +3,99%, las cuales son consideradas como pendientes que tienen poco efecto sobre la velocidad. Estas velocidades son mayores que en una curva de radio de 50 m, ya que al tener una mayor visibilidad, mayor longitud de circulación, el conductor puede alcanzar velocidades más altas. Luego de ello, decrece en pendientes positivas más altas, lo cual es coherente con la reducción de la velocidad con el aumento de la pendiente positiva. Y en pendientes negativas, también se reduce esa velocidad, lo cual está estrechamente relacionado con la mencionada percepción de riesgo del conductor.
Por otro lado, en la calibración de las ecuaciones en entre-tangencias horizontales fue realizada, utilizando los mismos rangos de velocidades utilizados en las ecuaciones de las rectas. Los resultados de estas ecuaciones se muestran en la tabla 1, en donde, se puede observar que la variable estadísticamente más significativa fue la longitud de la entre-tangencia, excepto en la ecuación en las pendientes longitudinales entre 6 a 10%, en donde se ha colocado un modelo constante. Este modelo se usa, cuando no existe relación estadística entre las variables analizadas, por lo que se elige el promedio de los valores de la variable dependiente como el valor que aparece en el modelo. Dado que no existe relación estadística, tampoco se podrá calcular el valor de R2.
Tabla 2. Ecuaciones calibradas de predicción de la velocidad de operación en entre-tangencias horizontales
| G (%) | Ecuación de predicción | R² | Rango de radios (m) | N° |
| 6 a 10 % | Vt85 = 69,69 | * | 22 - 260 | (8) |
| 4 a 5,99% | Vt85 = 0,03L+69,52 | 0,29 | 22 - 392 | (9) |
| 0 a 3,99% | Vt85 = 0,04L+73,69 | 0,37 | 22 - 435 | (10) |
| -3,99 a 0% | Vt85 = 0,05L+73,65 | 0,50 | 22 - 435 | (11) |
| -5,99 a -4% | Vt85 = 0,04L+72,68 | 0,47 | 22 - 392 | (12) |
| -10 a -6% | Vt85 = 0,07L+66,09 | 0,41 | 22 - 433 | (13) |
| Vt85 = velocidad de operación en la entre-tangencia horizontal en km/h, G = pendiente longitudinal de la carretera, L = longitud de la entre-tangencia horizontal, * = no es posible de calcular dado que es una ecuación constante, R2 = coeficiente de determinación, N° = número de ecuación. | ||||
Nótese que los valores de R2 de la tabla 2 son mayores a 0,25, lo cual es más bajo que en las curvas horizontales (tabla 1). Esto se debe a que en las entre-tangencias, al ser elementos rectos, el conductor tiene una mayor libertad para elegir su velocidad que en curvas, por lo que, consecuentemente existirá una mayor variabilidad de los datos. Esta variabilidad o dispersión reduce el valor de ajuste.
Si se usa las ecuaciones para entre-tangencias cortas, por ejemplo para una longitud de 30 m, las velocidades de operación serían: 69,7 km/h (6 a 10%), 70,4 km/h (4 a 5,99%), 74,9 km/h (0 a 3,99%), 75,2 km/h (-3,99 a 0%), 73,2 km/h (-5,99 a -4%), 68,2 km/h (-10 a -6%). Nuevamente se observa que las mayores velocidades en las entre-tangencias se encuentran en las pendientes entre 3,99 a 4%, luego, en pendientes ascendentes, se ve una disminución de la velocidad al igual que en pendientes descendentes, lo cual es coherente con lo observado en las ecuaciones de las curvas horizontales. Esta misma tendencia también se puede observar cuando se utilizan estas ecuaciones en longitudes más largas, por ejemplo en una entre-tangencia de 250 m: 69,7 km/h (6 a 10%), 77,0 km/h (4 a 5,99%), 83,7 km/h (0 a 3,99%), 86,2 km/h (-3,99 a 0%), 82,7 km/h (-5,99 a -4%), 83,6 km/h (-10 a -6%).
En resumen, las ecuaciones mostradas en la tabla 1 y 2 muestran un alto grado de coherencia con respecto a situaciones reales que se dan en la circulación de curvas y entre-tangencias horizontales. Cabe mencionar que los coeficientes de determinación para las ecuaciones de las curvas y entre-tangencias de esta investigación están entre 0,29 a 0,85, lo cual no difiere demasiado de otros estudios realizados en carreteras rurales, por ejemplo: 0,42 a 0,83 (García-Ramírez, 2014), 0,66 a 0,86 (Bennett, 1994), 0,62-0,86 (Memon et al., 2008), 0,71-0,72 (Crisma, Marchionna, Perco, Robba, & Roberti, 2005), 0,32-0,74 (Pérez, 2012), entre otros.
3.2 Validación de las ecuaciones
Para realizar la validación de las ecuaciones propuestas en la tabla 1 y 2, se seleccionaron 6 conductores para recorrer la misma ruta y con el mismo equipo de medición. Estos conductores tuvieron la misma distribución por sexo 50/50 y fueron seleccionados en base a los mismos criterios que los que participaron para la calibración. Así mismo, los vehículos estuvieron dentro del rango de parámetros de los vehículos utilizados en la calibración. También se siguió el mismo procedimiento de recolección y procesamiento de datos de velocidad que se empleó en la calibración, con lo cual se obtuvo la velocidad de operación en la mitad de las curvas y entre-tangencias horizontales, las cuales fueron comparadas con los resultados que generan las ecuaciones de la tabla 1 y 2. En esta comparación, se calcularon los errores de pronóstico y se hizo la prueba chi-cuadrado de bondad de ajuste para las ecuaciones que tuvieron predictor, mientras que para las ecuaciones constantes se usó la prueba t de Student. Los errores de pronóstico utilizado fueron: el error cuadrático medio (MSE), el error absoluto de la media (MAE) y el error absoluto porcentual de la media (MAPE). Estos valores y los relacionados con el Chi-cuadrado las ecuaciones de las curvas y de las rectas, se muestran en la tabla 3.
Tabla 3. Errores de predicción y valores Chi-cuadrado para las ecuaciones de velocidad, aceleración y desaceleración
| N° | n | Parámetros para la validación de las ecuaciones | ||||
| MSE (km/h)2 | MAE (km/h) | MAPE (%) | χ² | χ²5% | ||
| (2) | 25 | 63,75 | 6,59 | 9,61 | 0,93 | 36,42 |
| (3) | 15 | 47,05 | 6,07 | 8,48 | 0,66 | 23,68 |
| (4) | 14 | 26,17 | 4,37 | 5,71 | 0,34 | 22,36 |
| (5) | 12 | 39,85 | 4,79 | 5,99 | 0,50 | 19,68 |
| (6) | 17 | 46,43 | 5,51 | 8,12 | 0,68 | 26,30 |
| (7) | 39 | 30,61 | 4,61 | 6,48 | 0,43 | 53,38 |
| (9) | 12 | 42,76 | 5,17 | 7,12 | 0,59 | 19,68 |
| (10) | 10 | 29,62 | 4,94 | 6,23 | 0,37 | 16,92 |
| (11) | 9 | 52,47 | 5,99 | 7,26 | 0,64 | 15,51 |
| (12) | 13 | 50,35 | 6,16 | 7,87 | 0,65 | 21,03 |
| (13) | 37 | 66,77 | 6,92 | 9,64 | 0,93 | 51,00 |
| N° = número de ecuación, n = número de datos disponibles para la validación, MSE = error cuadrático medio, MAE = error absoluto de la media, MAPE = error absoluto porcentual de la media, χ² = Chi-calculado, χ²5% = Chi-crítico. | ||||||
En la tabla 3 se puede observar que los errores de predicción son bajos. El promedio de los errores de MAE es 5,56 km/h, el cual es más bajo que el error asumido en la estimación del tamaño muestral. El porcentaje de error máximo está alrededor del 10%, es decir, que si la velocidad real es de 80 km/h, las ecuaciones podría dar un valor entre 72 a 88 km/h, de todas maneras seguirá siendo menor a los 10 km/h que se usa como umbral de consistencia, sin embargo, para velocidades mayores o iguales a 100 km/h, se excederá de ese umbral. Cabe mencionar que es muy difícil alcanzar velocidades tan altas en carreteras de montaña, por lo que ese porcentaje no es de preocupación.
A pesar de existir errores bajos en las ecuaciones, se realizó la prueba Chi-cuadrado para decir si una ecuación es válida o no. En esta prueba, cuando el Chi-calculado es menor que el Chi-crítico, a cierto nivel de significancia, se podrá decir que no existe discrepancia entre los valores observados y los valores calculados con las ecuaciones. En este caso, todos los valores Chi-cuadrado calculados no exceden del Chi-crítico con un nivel de significancia del 5%, por lo tanto las ecuaciones analizadas son válidas.
Por otro lado, en la ecuación que tiene una constante se realizó la prueba de t de Student. Esta prueba evalúa si el grupo de datos de la validación es estadísticamente diferente al valor constante de la ecuación; por lo tanto, cuando el valor p sea mayor al nivel de significancia (en este caso del 5% o α=0,05), se podrá decir que no existen diferencias significativas entre el valor constante y los datos de la validación. Los resultados de la prueba t de Student para la ecuación 8 se pueden ver en la tabla 4. En esta tabla, se observa que el valor p de 0,291 es mayor a 0,05 por lo que los datos de velocidad de la validación no son estadísticamente diferentes que el valor constante de la ecuación, por lo tanto, ésta se puede considerar como válida.
Tabla 4. Errores de predicción y valores Chi-cuadrado para las ecuaciones de velocidad, aceleración y desaceleración
| N° | n | Parámetros para la validación de las ecuaciones | ||||
| Media (km/h) | σ(km/h) | IC95% | T | P | ||
| (8) | 15 | 67,83 | 6,59 | 9,61 | -1,10 | 0,291 |
| N° = número de ecuación, n = número de datos disponibles para la validación, σ = desviación estándar, IC95% = índice de confianza al 95% de confiabilidad error absoluto de la media, T = valor de la prueba t de Student, P = valor para decidir si existe diferencia estadística. | ||||||
En resumen, todas las ecuaciones calibradas fueron validadas usando información de 6 nuevos conductores y recorriendo la misma ruta en análisis. Cabe mencionar que las ecuaciones sólo son válidas entre rangos de parámetros para los cuales fueron desarrollados, por lo que cualquier valor fuera del rango puede conducir a resultados incoherentes.
4. CONCLUSIONES
El objetivo de este artículo fue calibrar ecuaciones de velocidad de operación en carreteras rurales montañosas de dos carriles, en donde se analice la influencia de la curva horizontal, la entre-tangencia horizontal y la pendiente longitudinal de la carretera. Luego del análisis de los resultados de esta investigación, se plantean las siguientes conclusiones:
Se lograron calibrar y validar 6 ecuaciones para predecir la velocidad de operación en curvas horizontales y 6 para predecirla en las entre-tangencias horizontales. En estas ecuaciones, el radio de curva circular horizontal y la longitud de la entre-tangencia, respectivamente, fueron estadísticamente significantes, lo cual es coherente con la literatura previa. Tanto en las curvas como en las entre-tangencias, la pendiente longitudinal de la carretera fue estadísticamente significativa para la predicción de velocidades operación.
Estas ecuaciones permitirán la elaboración de perfiles de velocidad en carreteras rurales de dos carriles en topografías montañosas. Este perfil se puede utilizar en los análisis de consistencia del diseño, lo cual es una herramienta para hacer modificaciones al diseño antes de que la carretera se construya, y con ello reducir la probabilidad de accidentes en este tipo de carreteras, que además de evitar muertes y lesiones de los usuarios viales, también permitirá ahorros por demanda pre-hospitalaria y hospitalaria, por ausentismo al trabajo, por pérdida de productividad, etc.
Este estudio tiene algunas limitaciones. En primer lugar, los datos sólo fueron recolectados en una carretera montañosa, cuando existen diversos entornos (paisaje, vegetación, etc.) que también pueden afectar a la velocidad de operación. También, el tamaño muestral es relativamente bajo (n=16), no obstante, está dentro de los límites de confiabilidad estadísticos. Además, es posible que la presencia del equipo de recolección influyera sobre el comportamiento del conductor, a pesar de habérsele indicado el alcance académico del estudio, sin embargo, eso no fue analizado por esta investigación.
A pesar de estas limitaciones, el presente estudio ayuda a entender los efectos que el radio de curva circular, la entre-tangencia y especialmente la pendiente longitudinal sobre la velocidad de operación de vehículos livianos. También, las ecuaciones fueron validadas y podrán ser utilizadas en futuros proyectos de carreteras montañosas. Finalmente, a pesar que la calibración de ecuaciones de velocidad en carreteras no es un tema nuevo, si lo es para la realidad ecuatoriana donde tradicionalmente se han adoptado parámetros de diseño de otros países. Esta investigación da el inicio a futuras calibraciones en otras carreteras con diversas topografías, con el fin de mejorar los diseños de las carreteras.