1. INTRODUCCIÓN
Mantener el voltaje de la carga dentro de los límites permitidos es cada vez más un reto para los operadores de sistemas de potencia, en razón de las restricciones de generación, transmisión y de la distribución de potencia reactiva en la red. Las cargas son variables independientes que cambian permanentemente y producen variaciones de voltaje y frecuencia en el sistema. Cuando los valores de estas señales se salen de ciertos márgenes permitidos, actúan dispositivos, tales como transformadores con cambio de taps bajo carga, que las llevan de regreso a su región segura. En el presente artículo se realiza el diseño y construcción de un transformador trifásico con taps en los lados primario y secundario. Una vez construido el transformador se efectúan pruebas de laboratorio con la finalidad de verificar su correcto funcionamiento, además de conocer su circuito equivalente, y realizar el control de voltaje en un sistema eléctrico de laboratorio.1 3 4 5 7 9 10 11 12
Se elabora una guía para el diseño y construcción de transformadores con el procedimiento para la obtención de los componentes necesarios, como características de los devanados y el núcleo. Esta guía tiene una interfaz amigable al usuario desarrollada en la plataforma MATLAB.
Posteriormente con los datos obtenidos del software se construye un transformador trifásico con taps en los dos devanados, sobre el cual se realizan pruebas eléctricas. Se implementa, además, un sistema eléctrico de potencia con el transformador construido para la comprobación del control de voltaje.
2. MARCO TEÓRICO
El proceso de diseño está dirigido a transformadores tipo seco. A fin de realizar el diseño de un transformador es necesario tener en cuenta varias especificaciones que cumplan con las normas técnicas de desempeño.
2.1 Software de Diseño de Transformadores Trifásicos Tipo Seco
El software está diseñado en la herramienta computacional GUIDE del programa MATLAB, la cual permite elaborar un sistema amigable con el usuario y a la vez realizar los cálculos que un transformador requiere para su construcción.
El usuario debe ingresar: potencia del transformador en kVA, voltaje primario en kV, voltaje secundario en kV, tipo de conexión del transformador, taps en el primario, y taps en el secundario. Si el usuario requiere la implementación de taps, debe ingresar además el rango de variación y el tamaño del paso.
El resultado final se despliega en pestañas diferentes, las cuales están divididas en:
-
Resultados del núcleo: dimensiones, pérdidas y peso del núcleo
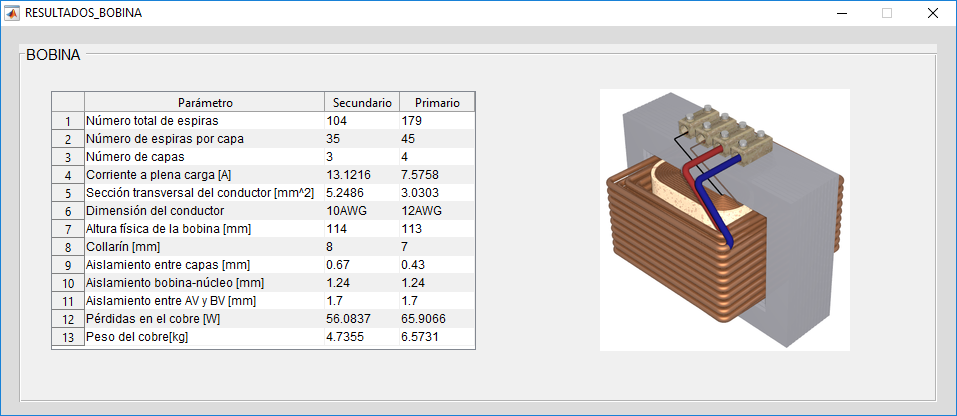
Resultados de las bobinas: calibre del conductor, corriente, pérdidas, peso, aislamiento y dimensiones de cada bobina.
Resultados de los taps: aumento de espiras para cumplir con las variaciones deseadas por el usuario, también los voltajes reales y teóricos de cada paso y sus diferencias.
Circuito equivalente del transformador diseñado: parámetros serie y paralelo del circuito equivalente en valores reales y en por unida.
Restricciones del Software
El programa está enfocado al diseño de transformadores trifásicos secos, con las siguientes restricciones:
-
Potencia entre 0,1 kVA y 350 kVA, la razón para restringir la potencia se debe a que los transformadores de mayor potencia y voltajes pequeños necesitan un conductor de sección grande y de una refrigeración mayor.
Voltaje mínimo 208 V, esto se debe a que al tener la máxima potencia de 350 kVA la corriente resultante es elevada, necesitando un conductor de sección muy grande.
Voltaje máximo 15 kV, se restringe este parámetro debido a que al tener un voltaje mayor, ya no se construyen transformadores secos sino sumergidos en aceite, debido a que requiere mayor aislamiento y mayor refrigeración.
2.2 Diseño del Transformador para el Laboratorio de Sistemas Eléctricos de Potencia
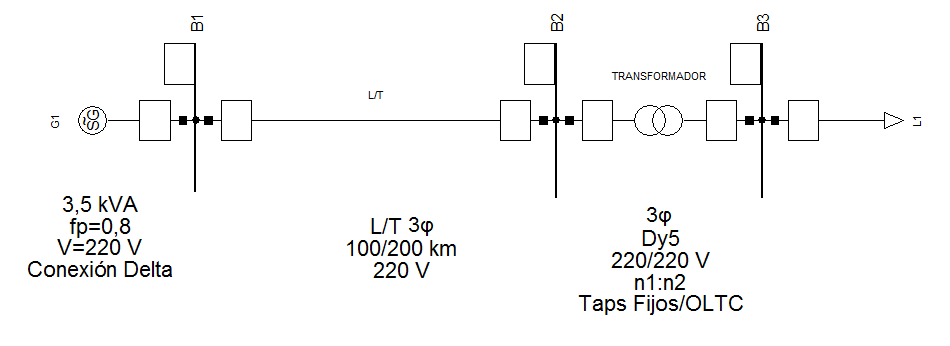
El diseño de un transformador para el Laboratorio de Sistemas Eléctricos de Potencia (SEP) necesita información de los elementos constitutivos del sistema a implementar, tales como: generador, modelo a escala de la línea de transmisión y carga, tal como se muestra en el diagrama unifilar de la Figura 1.
Para conocer la potencia de transformador requerido en este sistema, se toma como referencia la capacidad y el voltaje del generador, y se calcula la corriente con la ecuación (1):
La capacidad del transformador se calcula para una sobrecarga de 30%, es decir con una corriente de 12 A, por lo que la potencia será según la ecuación (2).
El transformador será dimensionado según los siguientes parámetros:
-potencia: 5 kVA,
-voltajes: 220 V/220 V,
-conexión Dyn5,
-taps devanado primario: +/- 5% con variación de 2,5%,
-taps devanado secundario: +/- 5% con variación de 1%.
Cálculo de Voltajes y Corrientes de Devanados
Los voltajes y corrientes de los devanados primario y secundario se calculan con las ecuaciones (3 ) a (6).
Selección de conductores
Como se trata de un transformador seco, se elige una densidad de corriente de 2,5 A/mm2, que dan secciones de conductor según las ecuaciones (7) y (8).
Conociendo la sección que deben tener los conductores se elige el calibre para cada devanado:
-
Devanado primario: 12 AWG, cuyo diámetro es 2,052 mm
Devanado secundario: 10 AWG, cuyo diámetro es 2,588 mm
Para la sección del núcleo se toma la constante =16 (RVR, 2017), ecuación (9):
2.3 Diagrama de Bloques del Software
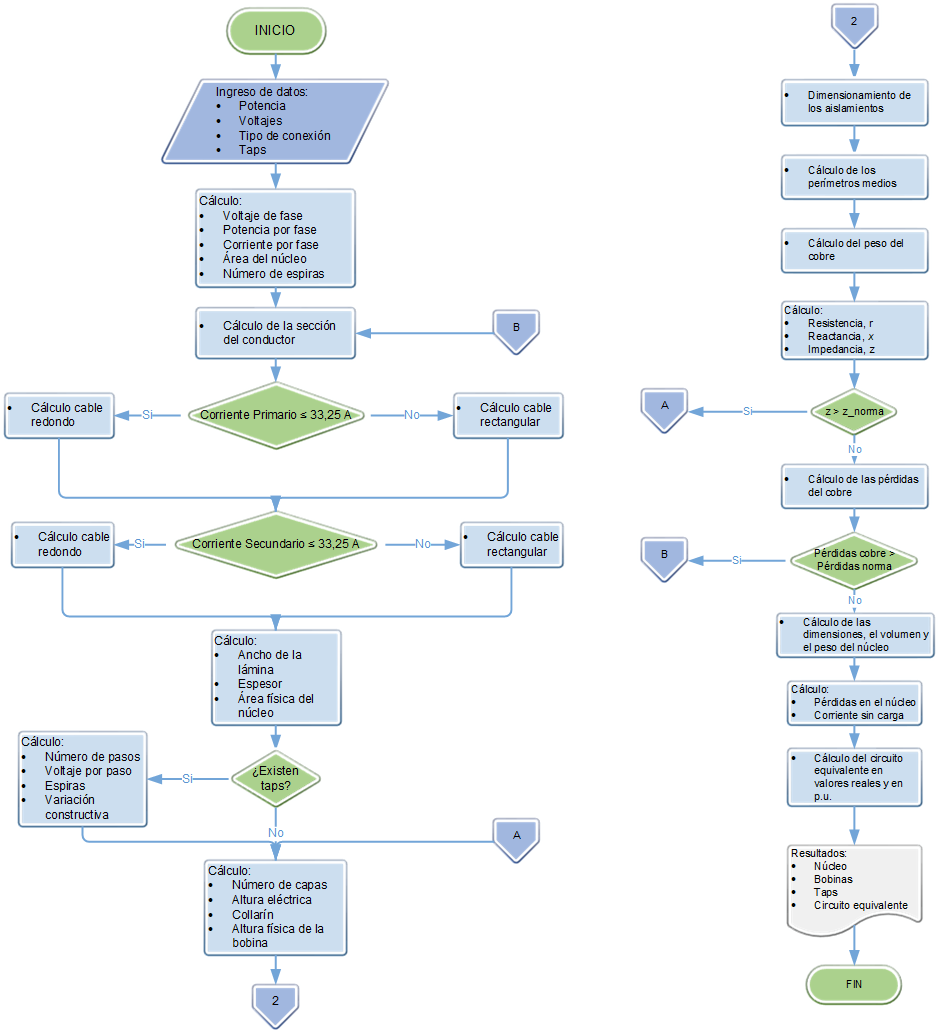
En la Figura 2 se detalla el diagrama de bloques del software de diseño de transformadores trifásicos tipo seco.
Se continúa con el cálculo de las dimensiones de la sección del núcleo: espesor y ancho de la lámina, utilizando las ecuaciones (10) y (11).
Cálculo del número de vueltas
El número de vueltas del primario se calcula con la ecuación (12).
Con la relación de transformación, se calcula el número de vueltas del secundario, mediante la ecuación (13):
Taps en el devanado primario
En el devanado primario se tienen cambios de +/- 5% con variación de 2,5%, ecuación (14):
Esto quiere decir que se tendrán dos taps por encima del nominal y dos por debajo del nominal, teniendo un total de: #Taps=5
Se sigue con el cálculo para aumentar espiras a la bobina a fin de cumplir con la variación requerida, ecuación (15):
Cada paso deberá aumentar 4 espiras del valor nominal, teniendo un total de espiras, según la ecuación (16):
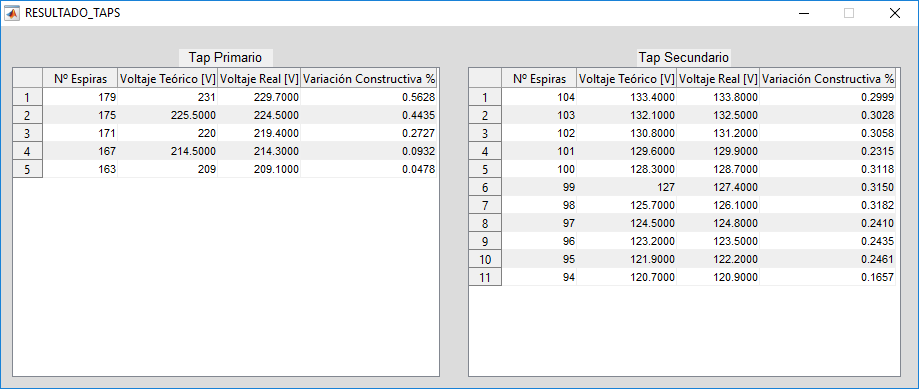
En la Tabla 1 se muestran los voltajes teóricos y reales que tendrá el transformador en el devanado primario con los diferentes cambios de posiciones de los taps.
Tabla 1. Valores de voltajes con taps en el devanado primario
| N° Espiras | Voltaje Teórico [V] | Voltaje Real [V] | Variación Constructiva [%] |
| 179 | 231,0 | 229,7 | 0,56 |
| 175 | 225,5 | 224,5 | 0,44 |
| 171 | 220,0 | 219,4 | 0,27 |
| 167 | 214,5 | 214,3 | 0,09 |
| 163 | 209,0 | 209,1 | -0,04 |
Taps en el devanado secundario
En el devanado secundario se tiene cambios de +/- 5% con variación de 1%, dando un rango según la ecuación (17).
Esto quiere decir que se tendrán cinco taps por encima del nominal y cinco por debajo del nominal, teniendo un total de: #Taps=11
Se continúa con el cálculo para aumentar espiras a la bobina a fin de cubrir con la variación requerida, ecuación (18):
Cada paso deberá aumentar 1 espira del valor nominal, teniendo un total de espiras según la ecuación (19).
En la Tabla 2 se muestran los voltajes teóricos y reales que tendrá el transformador en el devanado secundario con los diferentes cambios de posiciones de los taps.
Tabla 2. Valores de voltajes con taps en el devanado secundario
| Número Espiras | Voltaje Teórico [V] | Voltaje Real [V] | Variación Constructiva [%] |
| 104 | 133,4 | 133,8 | -0,29 |
| 103 | 132,1 | 132,5 | -0,30 |
| 102 | 130,8 | 131,2 | -0,30 |
| 101 | 129,6 | 129,9 | -0,23 |
| 100 | 128,3 | 128,7 | -0,31 |
| 99 | 127,0 | 127,4 | -0,31 |
| 98 | 125,7 | 126,1 | -0,31 |
| 97 | 124,5 | 124,8 | -0,24 |
| 96 | 123,2 | 123,5 | -0,24 |
| 95 | 121,9 | 122,2 | -0,24 |
| 94 | 120,7 | 120,9 | -0,16 |
Número de espiras por capa que tendrán los devanado primario y secundario
Con las ecuaciones (20) y (21) se calcula el número de espiras por capa en los dos devanados.
Cálculo de la altura eléctrica del devanado primario y secundario, ecuaciones (22) y (23).
Dimensión del collarín
Debido a que el voltaje de operación de cada devanado primario y secundario es 220 V y 127 V respectivamente, la clase de aislamiento según la Tabla 4 será de 1,2 kV con una distancia de aislamiento de 8 mm.
Cálculo de la altura física del devanado secundario y primario, ecuaciones (24) y (25).
Cálculo del aislamiento entre capas y bobinas y núcleo
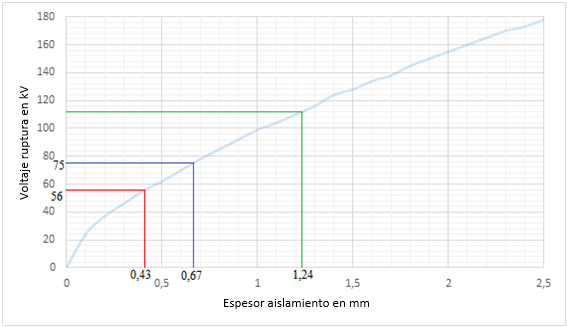
Se calcula primero el voltaje de ruptura, ecuaciones (26), (27) y (28).
Con base en la Figura 3 y los voltajes de ruptura obtenidos, se calcula el espesor de los aislamientos entre capas de espiras: Ais_capas1, Ais_capas2 y Ais_capas0.
Ais_capas1=0,43 mm
Ais_capas2=0,67 mm
Ais_capas0=1,24 mm
Cálculo del aislamiento entre bobinas
Con la clase de aislamiento de 1,2 kV, utilizando la Tabla 4, se obtiene que el aislamiento entre el devanado primario y el devanado secundario será de: ais21=1,7 mm
Cálculo de perímetros de las bobinas
Para obtener el perímetro, se parte del cálculo del espesor de la bobina, ecuaciones (29) y (30).
Con estos valores se calculan las dimensiones del frente y los costados de cada fase:
Dimensiones del frente, ecuaciones (31) a (35).
Dimensiones del costado, ecuaciones (36) a (40).
Una vez calculadas las dimensiones del frente y los costados, se calculan los perímetros medios de las bobinas, ecuaciones (41) y (43).
Peso del cobre
Con los perímetros medios de las bobinas, se pasa a calcular el peso total del cobre, ecuaciones (44) a (46).
Cálculo de la reactancia, resistencia e impedancia del transformador
La reactancia del transformador se calcula con las ecuaciones (47) a (52).
La resistencia de los devanados primario y secundario están dadas por, ecuaciones (53) y (54).
Las pérdidas en el cobre se calculan con las ecuaciones (55) a (57).
La impedancia del transformador se obtiene a partir de las ecuaciones (58) y (59).
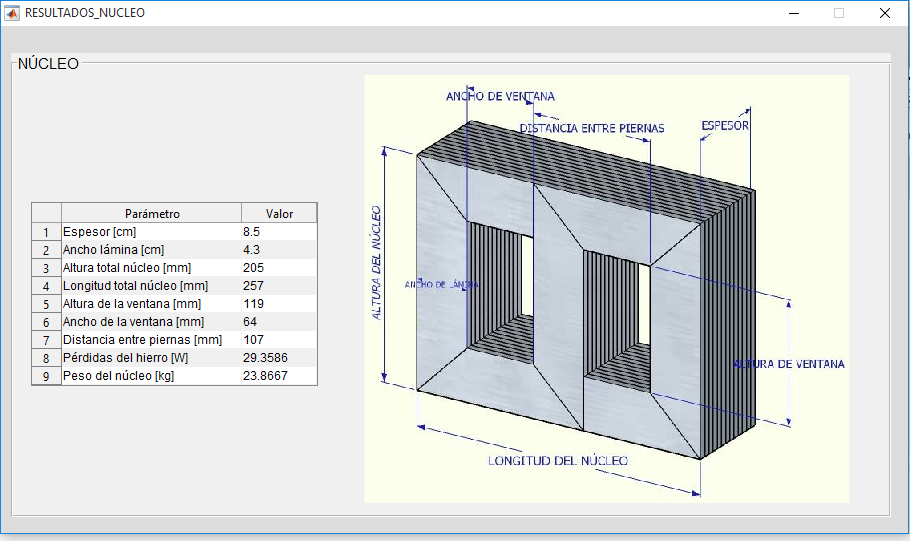
Cálculo de las dimensiones y pérdidas del núcleo
Con las dimensiones del núcleo se calcula primero las dimensiones de la ventana, ecuaciones (60) a (62).
Con los valores calculados se obtienen las dimensiones totales del núcleo, ecuaciones (63) y (64).
Volumen del núcleo, ecuaciones (65) a (68).
Peso del núcleo, ecuaciones (69) a (72).
Pérdidas en el hierro, ecuaciones (73) a (76).
Verificación de los parámetros
El cálculo de pérdidas en el hierro, con el valor de inducción de 13500 Gauss, se calcula con las ecuaciones (77) a (80).
La corriente de pérdidas se obtiene con la ecuación (81).
La corriente en vacío se calcula con la ecuación (82).
La corriente de magnetización se tiene de la ecuación (83).
2.4 Análisis y comparación de resultados
Una vez calculados los parámetros de diseño se compara con la Norma NTC3445 (NTC3445, 1992) a fin de comprobar que los valores obtenidos en el diseño cumplan los estándares.
Como se observa en la Tabla 3, el resumen de los resultados obtenidos en el diseño cumple con los estándares de la Norma NTC3445, por lo que se puede concluir que los cálculos realizados son correctos.
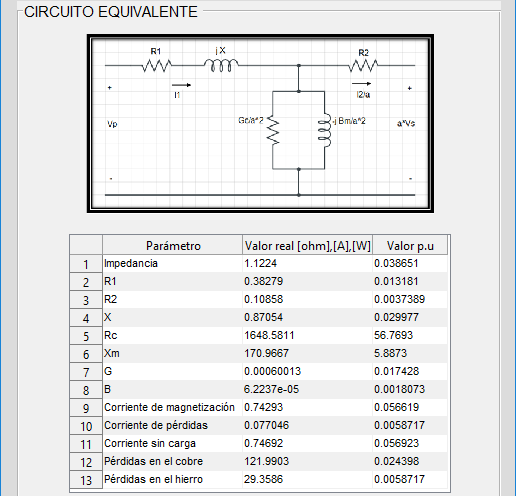
2.5 Circuito Equivalente del Transformador
Para determinar el circuito equivalente π es necesario definir una impedancia base en la que trabajará el sistema. El circuito equivalente del transformador será referido al primario, por lo que los valores base son los siguientes:
Donde:
SB: Potencia base monofásica
VB: Voltaje base línea a línea de la conexión delta
Por lo tanto, la impedancia base para el transformador se calcula con la ecuación (84).
Cálculo del valor de las resistencias de cortocircuito
Resistencia en p.u. del devanado primario, ecuación (85).
Resistencia en p.u. del devanado secundario, ecuación (86).
Cálculo del valor de la reactancia de cortocircuito en p.u. y valores reales, ecuaciones (87).
Cálculo del valor de la reactancia de magnetización y resistencia de pérdidas del núcleo, ecuaciones (88) y (89).
Los resultados obtenidos de la rama paralelo se encuentran referidos al secundario, por lo que los resultados de la reactancia de magnetización y resistencia de pérdidas se deben multiplicar por la relación de transformación al cuadrado, ecuaciones (90) y (91).
Se calcula la reactancia de magnetización y la resistencia de pérdidas del núcleo en valores de admitancia reales y en p.u., ecuaciones (92) a (94).
Donde:
Gc: conductancia en S
Bm: susceptancia en S
Por lo tanto, se tiene que:
2.6 Diseño del Cambiador de Taps con Carga
El conmutador de tap bajo carga (OLTC) se ubica comúnmente en el devanado secundario, realizando pasos finos de variación de voltaje. Debido a la baja corriente que maneja el transformador del Laboratorio se construye un OLTC que opere con contactores.
Diagramas de Tiempo del Cambio de Tap
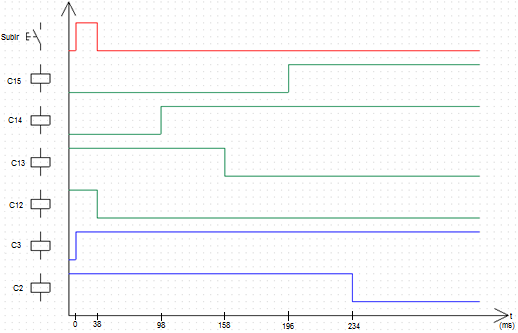
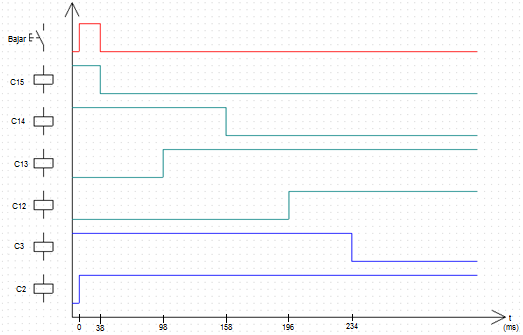
El funcionamiento del OLTC mediante contactores se puede observar en los diagramas de tiempo de las Figuras 4 y 5. En la Figura 4 se efectúa el cambio de un tap menor a uno mayor. En la Figura 5 se efectúa el cambio de un tap mayor a uno menor.
El programa es desarrollado en el PLC S7-400 de Siemens, en lenguaje Ladder para el cambio de taps bajo carga.
2.7 Circuito de Fuerza del OLTC
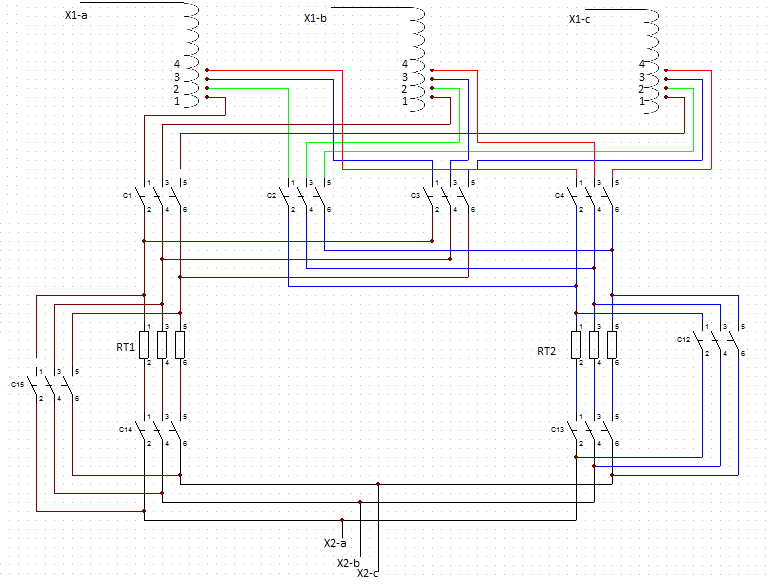
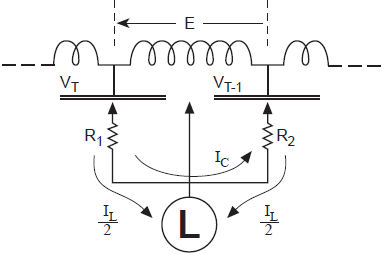
El circuito de fuerza de la Figura 6 presenta el esquema de conexión del OLTC, donde se muestran las bobinas del devanado secundario y la disposición de los contactores.
Los contactores C1, C2, C3 y C4 representan los taps que tiene el OLTC, mientras que C12, C13, C14 y C15 son los contactores para la transición de un tap a otro. Los contactores C12 y C15 cortocircuitan la resistencia de transición bajo operación normal del transformador. C13 y C14 conectan la resistencia de transición en el cambio de taps.
2.8 Dimensionamiento de la Resistencia de Transición
La resistencia de transición es la encargada de soportar el cambio en la posición de un tap a otro, para dimensionar esta resistencia es necesario conocer la máxima corriente que va a circular a través de ella.
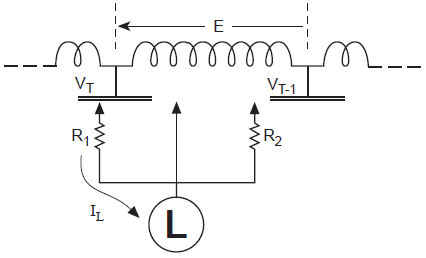
Cuando los contactores C14 y C13 de la Figura 6 se encuentran conectados durante la transición, existe una corriente circulante debido a que las resistencias R1 y R2 se encuentran conectadas. Por ello se realiza el siguiente análisis:
Cuando una de las resistencias se conecta en serie con la carga. Figura7
Cuando las dos resistencias de transición se encuentren conectadas, ecuaciones (95) y (96).
Figura8
En la carga se tendrá, ecuaciones (97) y (98).
Donde:
E: Voltaje entre taps
R: Resistencia de transición
Icirculante: Corriente que circula al tener las dos resistencias conectadas
IR1: Corriente en R1,
IR2: Corriente en R2
Para dimensionar la potencia que debe soportar la resistencia, se necesita conocer la corriente máxima que circulará por esta.
Por lo general, los valores de resistencia son pequeños para evitar que exista una caída de voltaje grande en la carga al momento de realizar la transición de un tap al otro, debido a que en un instante de la transición la resistencia se encuentra conectada en serie con la carga. Para el cálculo de la resistencia de transición se necesita conocer el voltaje que existirá entre cada paso de tap, ecuación (99).
Debido a que, en el devanado secundario, cada cambio de tap corresponde a una espira, el voltaje entre taps será:
Se utiliza una resistencia de 1 Ω para obtener una relación lineal entre la corriente y el voltaje medido, ecuaciones (100) y (101).
Con estas corrientes se puede calcular la caída de voltaje sobre la resistencia R1, ecuación (102).
Para conocer la potencia máxima que soportará la resistencia se realiza la comparación entre las corrientes de los casos analizados anteriormente:
La corriente máxima será la corriente de la carga: IL=13,12 A
La potencia de la resistencia será, ecuación (103).
La potencia que debe disipar esta resistencia es demasiado grande, en un tiempo de transición muy pequeño; por lo que, una alternativa para disminuir la caída de voltaje, la corriente y la potencia es colocar resistencias en paralelo de las siguientes características, ecuación (104).
La resistencia resultante al tener las cuatro en paralelo es, ecuación (105).
La caída de voltaje sobre la resistencia es, ecuación (106).
La potencia de cada una de las resistencias es, ecuación (107).
Por lo tanto, en la transición se tendrán cuatro resistencias en paralelo de 1 Ω y 10 W cada una.
2.9 Voltajes y Corrientes de Transición del Cambiador de Taps Bajo Carga
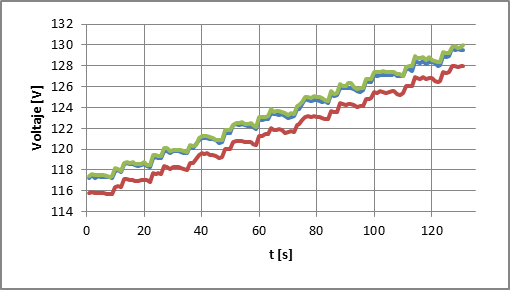
En la Figura 9 se observa que los voltajes de cada fase suben al aumentar la posición del tap y además durante el cambio de tap existe una caída de voltaje debido a la resistencia de transición.
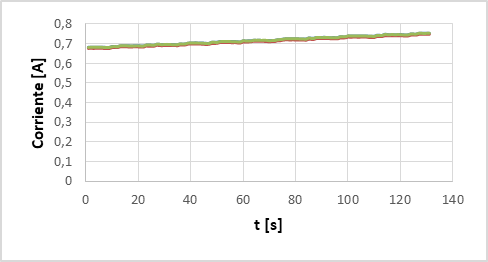
En la Figura 10 se muestran las corrientes en la transición de los cambios de taps, se puede ver claramente que no existe interrupción de las tres corrientes de fase.
3. RESULTADOS
3.1 Resultados del Diseño del Transformador
Los resultados obtenidos para el diseño del núcleo, la bobina y el circuito equivalente se muestran en las Figuras 11, 12, 13 y 14.
3.2 Resultados de las Pruebas en el Transformador
Resultados de la Prueba de Vacío
En la Tabla 4 se muestran los resultados obtenidos en la prueba de vacío, los cuales se encuentran dentro de los parámetros señalados en la norma NTC3445 (NTC3445, 1992) tanto de potencia como de corriente en vacío.
Para esta prueba las posiciones de los taps son: 1 en el primario y 11 en el secundario.
Tabla 4. Resultados prueba en vacío
| Fase | Vo [V] | Io [A] | Io [%] | Po [W] | Norma NTC3445 | |
| Po [W] | Io [%] | |||||
| R-S | 218,1 | 0,73 | 5,3 | 35 | 73 | 5,5 |
| S-T | 212,7 | 0,69 | 5,2 | |||
| T-R | 215,7 | 0,7 | 5,3 | |||
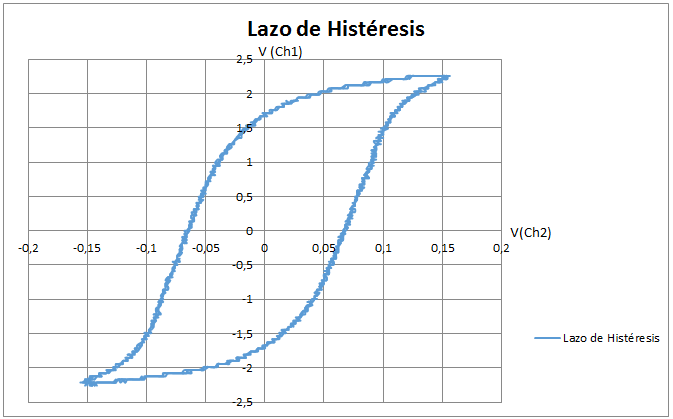
Curva de Histéresis y Cálculo Densidad de Flujo Magnético del Transformador
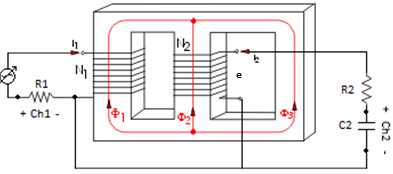
Para obtener la curva de histéresis del núcleo del transformador es necesario armar el esquema circuital de la Figura 15, con los siguientes elementos:
R1 = 1 Ω, R2 = 390 kΩ, C2 = 1 µF, N1 = N2 = 104
Debido a que el núcleo en estudio es de una unidad trifásica y que se halla ya armado, se utilizan dos devanados secundarios conectados en estrella.
La corriente I1 se captura a través de la resistencia R1 en el canal Ch1 y el voltaje e sobre el capacitor C2 en el canal Ch2 del osciloscopio. En la Figura 16, se muestran los valores de voltaje obtenidos en los canales 1 y 2 del osciloscopio.
Para obtener el lazo de histéresis en unidades de Teslas y A/m es necesario realizar el siguiente análisis aplicando las leyes de Ampere y Faraday sobre las bobinas 1 y 2, respectivamente, ecuaciones (108) y (109).
El voltaje inducido y la densidad de flujo en la bobina 2 se calculan con las ecuaciones (110) y (111).
Donde B: Densidad de flujo magnético en T, H: Intensidad de campo magnético en A/m, e: Voltaje en la segunda bobina en V, L: Longitud media del núcleo en m, A: Área del núcleo en m2, VC: Voltaje del capacitor en V.
Cálculo del Circuito Equivalente
Con los resultados obtenidos en las pruebas de vacío y cortocircuito se calcula el circuito equivalente del transformador. Se realiza un ejemplo de cálculo para la posición nominal de los taps con las bases: ,
Por lo tanto, la impedancia base para el transformador en los dos lados está dada por la ecuación (112).
Cálculo del valor de la resistencia de los devanados en conexión delta, ecuación (113).
Cálculo del valor de la impedancia de cortocircuito en conexión delta, ecuación (114).
Cálculo del valor de la reactancia ecuación (115).
Cálculo del valor de la reactancia de magnetización y resistencia de pérdidas del núcleo
La potencia de pérdidas en vacío está dada por la ecuación (116).
De donde se obtiene el factor de potencia de la rama paralelo, ecuación (117).
Con lo que la corriente de pérdidas se calcula con la ecuación (118).
La corriente de magnetización se calcula con la ecuación (119).
Por lo tanto, la resistencia de pérdidas en el núcleo Rc, la reactancia de magnetización Xm, la conductancia Gc y la susceptancia Bm, se calculan con las ecuaciones (120) a (125).
4. CONCLUSIONES
Se ha podido comprobar que los parámetros obtenidos en el diseño: R=0,705 Ω; X=0,871 Ω y Z=1,122 Ω, realizado para el transformador con la interfaz gráfica son similares a los del transformador construido: R=0,718 Ω; X=0,84 Ω y Z=1,105 Ω, con errores de: 1,84%, 3,55% y 1,51%, respectivamente.
Al realizar las pruebas eléctricas en el transformador, se pudo constatar que los resultados de las pérdidas: 123,7 W son similares al diseño realizado de 122 W, con la variación en las pérdidas de cobre debido a la presencia del OLTC y conexiones exteriores de los equipos de medición.
Una vez realizada la prueba de la curva de histéresis del transformador se comprueba que la densidad del flujo magnético del material es 13800 Gauss, la cual es similar a la utilizada en el diseño de 13500, comprobando que la calidad del material ferromagnético es la adecuada.
En las pruebas realizadas con el OLTC, se verifica que la carga no se desenergiza en ningún momento mientras se efectúa la transición de una posición a otra.
La resistencia del transformador en el diseño es de 2,42% y aumenta a 2,47% en el transformador construido.
Los parámetros obtenidos en las diferentes pruebas realizadas al transformador construido, como pérdidas en el núcleo 35 W, pérdidas en el cobre 123,7 W y corriente de excitación 0,7 A, se encuentran dentro de los valores establecidos en la norma especificada, la cual señala que no deben superar 73 W, 195 W y 0,722 A, respectivamente.