1. INTRODUCTION
Cognitive robots are endowed with intelligent behavior, which allows to learn and reason how to behave in response to complex goals in a real environment. In general, its application focuses on creating long-term human-robot interactions. In consequence, this field of study is centered on developing robots that are capable of perceiving the environment and other individuals to learn from experience and to adapt their behavior in an appropriate manner (Aly, Griffiths, y Stramandinoli, 2017). As with human cognition, robot cognition is not only good at interaction but that interaction is indeed fundamental to build a robotic cognition system.
Inspired by the proxemics studies developed by Hall (1963), some conventions have been established in robotics in order to avoid the intimate and social spaces of humans depending of the task, the situation, and even of specific human behavior reaction. For example, Chi-Pang, Chen-Tun, Kuo-Hung, y Li-Chen (2011) discuss different types of personal space for humans according to the situation, e.g., they assume an egg-shaped personal space for the human while it is moving, in order to have a long and clear space to walk (giving the sense of safety). For this, they consider that the length of the semi-major axis of the potential field is proportional to the human velocity. In Scandolo y Fraichard (2011) it is used the personal space in their social cost map model for path simulation. In Guzzi, Giusti, Gambardella, Theraulaz, y Di Caro (2013) it is incorporated a potential field that dynamically modifies its dimensions according to the relative distance with the human to avoid occlusion events or “deadlocks”. In Ratsamee, Mae, Ohara, Kojima, y Arai (2013), a human-friendly navigation is proposed, where the concept of personal space or “hidden space” is used to prevent uncomfortable feelings when humans avoid or interact with robots. This is based on the analysis of human motion and behavior (face orientation and overlapping of personal space).
According to proxemics research, the actual shape of the social zones is subject to tweaking and the preferred distances between humans and robots depend on many context factors. Most of them have growing costs as the distance to some area decreases (, Pandey, Alami, y Kirsch, 2013). Due to the diversity of models for the social zone, find the optimal selection of distances and shapes results also a key challenge. For example, Pacchierotti, Christensen, y Jensfelt (2006) evaluates through an experimental methodology the social distance for passage in a corridor environment to qualitative determine the optimal path during the evasion. The hypothesis that people prefer robots to stay out of their intimate space when they pass each other in a corridor is qualitatively verified. On the other hand, Kuderer, Kretzschmar, y Burgard (2013) proposes an approach that allows a mobile robot to learn how to navigate in the presence of humans while it is being tele-operated in its designated environment. It is based on a feature-based maximum entropy learning to derive a navigation policy from the interactions with the humans. Other approaches considers that the comfort of the individual is not only guaranteed through the avoidance of these social zones, but also the dynamics during the meddling events, i.e., to give a natural, smooth and damped motion during the interaction by considering these zones as flexible potential zones (Herrera, Roberti, Toibero, y Carelli, 2017).10
In this paper, the “hidden-dimension” or social space of humans is characterized by the robot with previous experiences. It consists of taking measurements in front of the robot to determine zones of the lowest human-presence around itself. Under the hypothesis that this zone can be modeled like elliptical potential fields, the best elliptical zone that fits to the zone with lowest human presence is defined as the cognitive social field. The use of this inferred ellipse is based on the hypothesis that humans avoids other individuals in the way they would like to be avoided (Fong, Nourbakhsh, y Dautenhahn, 2003). With the inferred social zone, the design of a null-space approach (NSB) for trajectory tracking control and pedestrian collision avoidance is proposed. The first-priority task consists in keeping out of social zones of humans, which are defined as elliptical potential fields which are moving with a non-holonomic motion, and whose dimensions are defined as mentioned. On the other hand, the secondary task is related to follow the predefined trajectory. The good performance of the designed control is verified experimentally.
In this way, Section 2 presents a novel algorithm to estimate the social zone of the robot based on laser measures and acquisition, storage and update policies during direct interaction with humans. Later, in Section 3, the estimated dimensions of the social zone are used to infer a social potential field for human obstacles. Following with this, in Section 4 the avoidance of this field and the trajectory tracking tasks are included as part of a null-space based control design. In Section 5, the performance of the algorithm is tested through experimentation with a mobile robot Pioneer 3AT which is navigating in a structured human-shared scenario. Finally, some conclusions are presented in Section 6.
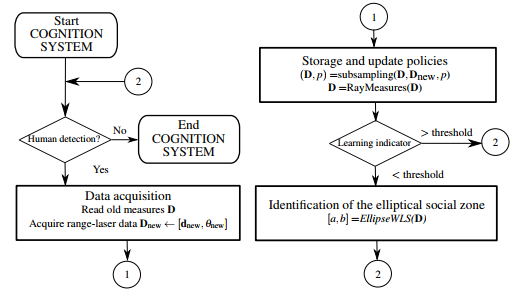
2. COGNITION SYSTEM
Learning from the experience is doubtlessly a human quality that must be used by robots to understand and reproduce human behaviors, which enhances the human-robot interaction (Fong y cols., 2003).
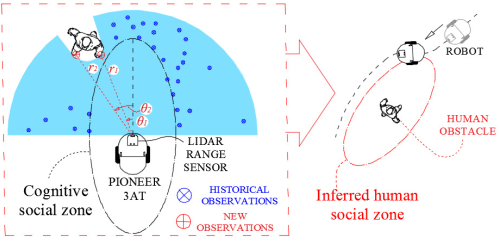
The humans unconsciously define a social zone for the robot while avoid it, which is represented by the the non-meddling zone, i.e. the region near to the robot that has been not invaded by the human. This section presents a cognitive system in which the robot learns how to avoid humans by analyzing how the human avoids the social space of the robot (see Fig. 1). In this manner, it is proposed to use this hypothesis to infer a social zone for collision avoidance with humans. For this, elliptical social zones have been frequently chosen by researchers to represent human obstacles, which have proved to improve the social acceptance of robots navigating between humans (Rios-Martinez, Spalanzani, y Laugier, 2015). In this way, consider the equation of the ellipse in the robot framework expressed in polar coordinates by
where
2.1 Data acquisition
For each detection event, new laser measurements
These measures are organized in a vector of nt-distances
In this manner, new observations of humans, compactly expressed by
2.2 Storage and update algorithms
Let N=size(D) be the size of the points-cloud, which is limited by the need of reducing computational costs, outliers observations, and redundant data. These objectives are reached by using a subsampling procedure, which is the random process of reducing the sample size from K to k<K (subsampling performed in one step), where each observation remains in the subsample with probability k=K. If a storage quota of C observations is also considered, then it is required to perform a subsampling every time that the number of stored observations N exceeds the quota C, in which each observation has a probability C=N of remaining in the subsample (recursive subsampling).
This task is reached by using Algorithm 1, in which new observations are properly incorporated in D so that all observations (regardless of when they are acquired) have the same probability p of belonging to the points-cloud.
The procedure consist of initializing a empty points-cloud (N=0) and an acceptance probability of new observations p=1. The algorithm incorporates all the observations acquired to the pointscloud until N+nt>C. When it happens for the first time, C observations must be subsampled and the remaining observations must be deleted.
Then, probability of belonging to the points-cloud is updated to p=C/N, and N is set to C. From this moment, all new observations must undergo an acceptance process in order to match their probability with the probability p of the observations acquired previously (steps 6-10 of the Algorithm 1). Later, if the quota is still exceeded a new subsampling is performed and the acceptance probability is decreased (steps 11-13 of the Algorithm 1). In this way, all observations (originals and news) have the same probability p of belonging to the points-cloud.
Algorithm 1 (D,p)=subsampling(D,Dnew,p)
1: N=size(D)
2: nt=size(Dnew)
3: if N+nt≤C then if the storage quota is not exceeded
4: D=[D;Dnew]
5: else. if the storage quota is exceeded
6: for i=1:nt do for each new observation
7: u=rand(0,1) uniform random number
8: if u>p then acceptance-rejection procedure
9: i-th new observation is deleted
10: nt=nt-1
11: if N+nt>C then if the quota is still exceeded
12: subsample C obs. without replacement.
13: p=pC/N update the acceptance probability
14: N=C
15: else
16: D=[D;Dnew]
Subsequently, a process is incorporated to avoid the agglomeration of observations in specific angular direction from the robot framework, in order to unify the angular distribution of the pointscloud. For them, the number of measures per ray is also limited by considering only the ˜C nearest measures to the robot, and measures in excess are discarded (see Algorithm 2).
Algorithm 2 D=RayMeasures(D)
1: for i=1:180 do for each angle
2: #
3: if #
4: Leave only the
2.3 Identification of the elliptical social zone
The identification procedure consists of estimating the parameters a and b that minimize the following functional
where
and the weight matrix is the NxN diagonal matrix
W=diag({wi}).
In this case, the weight factors are defined as
where
Then, the solution of the optimization problem is given by
Algorithm 3 performs this estimation.
Algorithm 3 [a;b]=ElipseWLS(D)
1: r = D(:,1),
2: for i = 1:N do for each observation
3: rmin,i=min(r(
4: Y(i,:)=[
5: X(i)=1/ri2
6: W(i,i)=wi
7:
8:
2.4 Learning indicator
Infer a social space requires to define a learning indicator during the cognition stage, which determines a condition where the ellipse dimensions can be well defined, and in consequence a social zone for human collision avoidance algorithms could be estimated.
Let
where
In this manner, let
In this manner, the points-cloud can be only used for estimating a social zone when
3. SOCIAL POTENTIAL FIELD
As mentioned, social zones are interpreted as repulsive potential fields, which guarantee the human comfort during interactions. Thereby, once that the dimensions of the minor and major axis of an elliptical social zone have been inferred of the cognition system, an elliptical potential field is defined as follows.
Let
where a is the major-axis length of the elliptical Gaussian form, and b is the minor-axis length (see Fig. 3). The time-dependency of these variables has been neglected to simplify the notation.
In order to define the Jacobian that relates the potential variation with the motion of the robot, consider the time derivative of the potential as follows:
Solving this expression through algebraic steps, it results
where,
If the rotation matrix is defined as,
then it results possible to express (4) in the xy global framework, i.e.,
where,
Similarly for the human position,
where,
If additionally it is considered a non-holonomic motion for the human gait (Arechavaleta, Laumond, Hicheur, y Berthoz, 2006; Leica, Toibero, Roberti, y Carelli, 2014),
then operating with (6), it results,
where Vh and wh are the linear and angular of the human obstacle, respectively.
In this way, by substituting (5) and (7) in (4), results that
Therefore, the total repulsive effect over the robot in a position xr:=(xr;yr) is calculated as the sum of all the repulsive effects Vhj generated by n human obstacles in the shared scenario, i.e.
where
4. NULL-SPACE BASED CONTROL
Consider a robot that must develop a task in a human-shared environment fulfilling two objectives: trajectory tracking and collision avoidance with humans.
4.1 Principal task: Collision avoidance with humans
The meddling avoidance of the robot into human social zones is defined as the principal task. Thus, if V is considered as the task variable, then from (8), the minimal norm solution for this task is expressed through the control action
where the desired potential is Vd=0,
4.2 Secondary task: Trajectory tracking control
For the secondary task, consider a desired trajectory xt=[xt,yt]T , which must be tracked by the robot. In this way, the control objective is based on controlling the robot position xr=[xr,yr]T. For this, consider an error-proportional solution for the secondary task expressed through the Cartesian robot velocities as
where
4.3 Solution for a differential drive mobile robot
Consider the non-holonomic kinematic model of the robot expressed as,
where xr=[xr,yr]T is the robot position located on the symmetry axis between the wheels at a distance of r from the wheel axis,
Thereby, consider an inverse kinematic solution given by
where
where
5. EXPERIMENTATION
5.1 Experimental setup
The experimentation is developed in a structured scenario, which is scanned by a ceiling camera. The algorithm consists in capturing color images in each sample time, where the posture of each experimental individual, i.e. the robot and the human obstacle is characterized through the centroid positions of two colors, easily distinguishable (Colors are neither in the scenario nor in the experimental individuals.).
Additionally, a Pioneer 3AT robot is equipped with a 180-degrees LIDAR sensor (one degree of resolution), and the measures and commands to the robot are sent through a client/server WiFi connection. In this case, a sample time of ts = 0.1[s] is considered to control the robot during the experiment. The selected parameters for the experiments are shown in Table 1.
5.2 Cognition system results
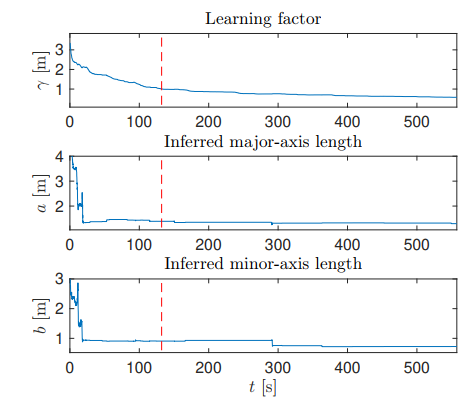
In Fig. 4, it is presented the trajectory followed by the robot when captures the information. Note that, at first, the robot takes measurements, which are not representative to infer a social zone, but they are discarded in an iterative way during the experiment, and only the points in the nearest to the robot are stored and updated according to the previous defined policies.
At the beginning of the experiment, the robot tracks the trajectory without avoiding the human obstacles, i.e. while
Along time, the inferred major and minor-axis length achieves a bounded and practically constant condition, even when the learning factor continues decreasing (see results before dashedred-line in Fig. 5).
Once that the spread of the points-cloud is well-defined around the social zone of the robot, i.e. when
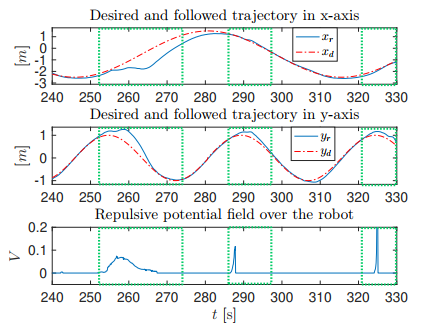
5.3 Motion control results
The control errors and the trajectories generated during a timelapse of the experiment are shown in Fig. 6. Marked with green boxes, some collision avoidance events are shown, where the controller is able to guarantee the convergence of the trajectories after that the collision is avoided. Note that the control objectives are fulfilled in a priority order as expected (see video clip in https://youtu.be/acpYu0I3XDI).
6. CONCLUSION
This paper has presented a novel cognition system to infer a social field from laser measurements. For this, acquisition, storage and update policies have been proposed to build the social zone of the robot based on direct human-robot interactions. Later, this learning allows representing human obstacles as elliptical potential field with non-holonomic motion, which according to the researchers, improves the social acceptance of the mobile robots during human-robot interactions. Following with this, a null-space based (NSB) motion control to track a trajectory and to avoid pedestrians by considering a differential drive mobile robot is proposed. Finally, the algorithm has been tested through experimentation, and the good performance of the cognition system and motion control trategy has been verified. Based on the hypothesis that humans avoids other individual in the way they would like to be avoided, authors believe that the proposed algorithm improves the social acceptance of mobile robot during human-robot interactions, because it is capable to learn this behavior and reproduce it during the pedestrian collision avoidance.