1. INTRODUCCIÓN
Para el dimensionamiento de un sistema de radiocomunicación se pueden utilizar diferentes modelos de propagación, ya sean, empíricos, teóricos o semi-empíricos.
Los modelos de propagación se utilizan para predecir las pérdidas medias en la trayectoria en función de variables, tales como altura de las antenas transmisora y receptora, frecuencia y distancia. La predicción de las pérdidas de trayectoria es muy importante cuando se trata de determinar la cobertura de redes inalámbricas, ya que en este medio es donde se presenta mayor cantidad de efectos negativos que provocan atenuación de la señal transmitida (He R. 2010). El modelo de propagación log-distancia es muy popular cuando se trata de modelación de las pérdidas de trayectoria (Rappaport, 2002). En este modelo, el exponente de pérdida de trayectoria depende del entorno de propagación de las ondas de radio y se lo puede determinar en base a los datos de mediciones realizadas, dicho exponente indica que tan rápido aumentan las pérdidas en función de la distancia (Rappaport, 2002), (Cox, 1984).
He (2011) realizó mediciones de banda estrecha a 930 MHz en un sector de la línea férrea de alta velocidad de China. El modelo obtenido se basa en el modelo de pérdidas de trayectoria de shadowing log-normal considerando el efecto de la distancia de referencia.
Aboul-Dahab (2010) tomó en cuenta mediciones de propagación efectuadas en diferentes lugares del planeta en la banda de frecuencia de 3.5 GHz considerando redes con diferentes topologías de la tecnología WIMAX. En el proyecto se utiliza Least Square Aproximation para el cálculo de los límites superiores e inferiores de las pérdidas de trayectoria y se realiza una comparación entre diferentes modelos.
Los estudios desarrollados se han direccionado en determinar modelos de propagación a partir de mediciones. Debido a que los modelos existentes se han obtenido en base a mediciones realizadas en lugares específicos del planeta que no son lo suficientemente precisos si se aplican en regiones distintas. Para la determinación de las pérdidas de propagación en la ciudad de Quito se requieren modelos que se ajusten de mejor manera a las condiciones geográficas y a las características de propagaciones intrínsecas y estocásticas de dicha región.
El presente artículo se encuentra estructurado de la siguiente manera. En la sección II se incluye el fundamento matemático utilizado para los posteriores análisis, ya que se presentan las expresiones matemáticas de los modelos de propagación utilizados en este proyecto. En la sección III se describe la metodología de medición que se aplicó para obtener los valores de pérdida de trayectoria. En la sección IV se propone la obtención del modelo matemático de pérdidas de trayectoria adaptado a las condiciones de medición y a las características del entorno. En la sección V se muestra el análisis de los modelos adaptados de pérdidas de trayectoria; la evaluación se realiza con dos métodos estadísticos, que permiten determinar si el modelo obtenido es adecuado. En la sección VI se describen las conclusiones del trabajo desarrollado.
2. MODELOS DE PROPAGACIÓN
Para este estudio se toman como referencia algunos modelos de propagación conocidos para su posterior adaptación a las mediciones realizadas en la ciudad de Quito. Las expresiones matemáticas para el cálculo en dB de las pérdidas de trayectoria con los modelos de propagación, se incluyen en la siguiente tabla y constituyen el fundamento matemático para el análisis posterior.
Tabla 1. Modelos de propagación analizados
| Modelos de Propagación | Expresiones matemáticas de pérdidas |
|---|---|
| Espacio, IEEE Vehicular (1988) |
|
| Egli, IEEE Vehicular (1988) |
|
| Okumura, IEEE Vehicular (1988) |
|
| Okumura / Hata, European Commission (1999), UIT-R (2009) |
|
| Cost -231, European Commission (1999) |
|
| Walfisch, Giménez (2011), European Commission (1999) |
|
A continuación se describen algunos de los parámetros que se incluyen en la tabla anterior:
hte - la altura de la antena transmisora,
hre - la altura de la antena receptora,
LF - Pérdidas de propagación en el espacio libre,
Amu - Atenuación media relativa del espacio libre que se determina mediante curvas.
G(hte ) - Factor de ganancia de la altura de la antena de transmisión:
G(hre ) - Factor de ganancia de la altura de la antena móvil:
GAREA - Ganancia debido al tipo de entorno (Factor de Corrección) que se determina mediante curvas.
a(hre) - Factor de corrección por la altura de la antena móvil o receptora, que depende del tamaño de la zona de cobertura.
Para una ciudad pequeña o de tamaño medio, el factor de corrección de la antena móvil a(hre) está dada por:
Para una ciudad grande, el factor de corrección a(hre) está dado por:
cm - Factor de corrección.
El factor cm, se establece en Dalela (2012), tiene un valor de 0 dB para zonas suburbanas y zonas abiertas, y 3 dB para zonas urbanas.
3. METODOLOGÍA DE MEDICIÓN
La metodología de medición se dividió en seis etapas que se describen a continuación.
3.1 Definición de la zona de medición
Inicialmente se identificó la zona de cobertura donde se realizarán las mediciones, ya que un factor muy importante que influye en las pérdidas de trayectoria es la característica geográfica del lugar. Esta zona se eligió para que permita tener una referencia adecuada y sea posible generalizar los resultados. La zona de cobertura seleccionada fué el campus universitario de la Escuela Politécnica Nacional en la ciudad de Quito.
Debido a que este proyecto se lo realiza para el cálculo de pérdidas de trayectoria en microceldas, la distancia de cobertura no sobrepasa los 350 metros.
3.2 Puntos de medición
Una vez identificada la zona de cobertura se seleccionó con exactitud un número importante de puntos donde se realizaron las mediciones de la potencia recibida. Y se identifican los escenarios que se tienen entre el transmisor y receptor para diferenciar la influencia de cada uno de ellos.
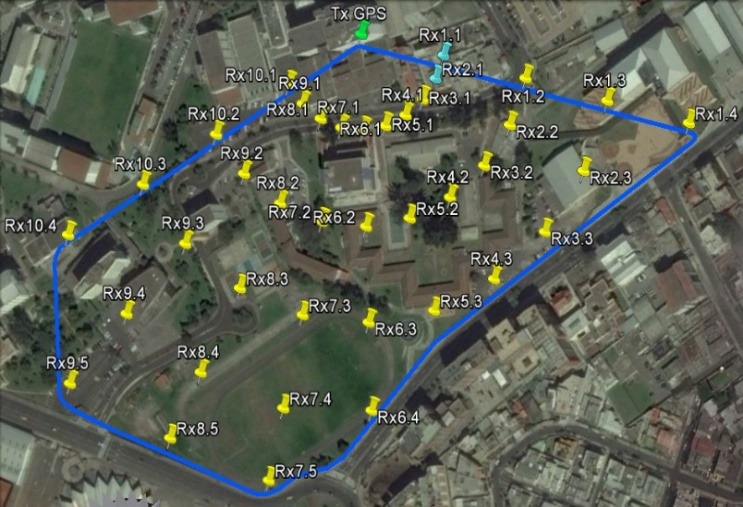
Debido a las características de la zona de cobertura, se escogieron 39 puntos de medición, que se encuentran distribuidos considerando ángulos de azimut de 15°, es decir que desde el transmisor se tienen 10 rutas de medición. En cada azimut las distancias de separación de la antena receptora hacia la antena transmisora fué de 70, 140, 210, 280 y 350 metros. Para la ubicación precisa de los puntos de medición se utilizó un GPS.
En la Figura 1 se observa la distribución de los puntos de medición en la zona de cobertura planteada y la ubicación del transmisor.
3.3 Escenarios de medición
En la zona seleccionada se identificaron tres escenarios: línea de vista, sin línea de vista con obstrucción por edificios y sin línea de vista con obstrucción por árboles. La agrupación de las mediciones por el tipo de escenario permitió obtener valores precisos de potencia de recepción, que se tomó en cuenta para obtener modelos de pérdidas de trayectoria para cada escenario.
3.4 Selección del rango de frecuencia de medición
El rango de frecuencias seleccionado se encuentra desde los 928 MHz hasta los 960 MHz. Utilizando un analizador de espectros se verificó que dicho rango de frecuencias no se encontraba ocupado durante la realización de las mediciones.
Las mediciones de los parámetros de antenas, potencia de transmisión y recepción se ejecutaron cada 1 MHz.
3.5 Potencia real de transmisión y recepción
Con el uso de un medidor de potencia RF se estableció con exactitud la potencia real transmitida a la salida del generador de señales que se utilizó como transmisor.
Utilizando un analizador vectorial de redes se determinaron los parámetros de VSWR de las antenas transmisora y receptora en el rango de frecuencias de medición, con la finalidad de establecer el nivel de potencia real transmitido aplicando el parámetro de eficiencia de acoplamiento de las antenas.
En el lado del receptor se utilizó un analizador de espectro configurado con las características de la antena receptora para registrar la potencia real recibida.
Los equipos utilizados en este proyecto se enumeran en la Tabla 2.
Tabla 2. Equipos utilizados en las mediciones
| LISTA DE EQUIPOS UTILIZADOS | |||
|---|---|---|---|
| EQUIPO | MARCA | MODELO | RANGO DE FRECUENCIA |
| GENERADOR DE SEÑALES | Anritsu | MG3691C | 0,1 Hz a 10 GHZ |
| MEDIDOR DE POTENCIA | Tektronix | PSM4120 | 10 MHz a 8 GHz |
| ANALIZADOR VECTORIAL | Keysight | N9914A | 30 kHz a 6,5 GHz |
| ANALIZADOR DE ESPECTROS | Anritsu | MS2711E | 9 kHz a 3 GHz |
| ANTENA LOG-PERIÓDICA(TRANSMISORA) | A. H. Systems | SAS-510-4 | 290 MHz a 4 GHz |
| ANTENA MINI.MAG(RECEPTORA) | Smarteq | 1140.26SMA | 824 a 960 MHz – 1710 a 2170 MHz |
3.6 Especificación de las condiciones de medición
Las condiciones de medición se especifican en la Tabla 3 y por tanto definen los rangos de aplicación de los modelos que se obtuvieron en el presente trabajo.
4. OBTENCIÓN DEL MODELO ADAPTADO DE PÉRDIDAS DE TRAYECTORIA PARA LA CIUDAD DE QUITO
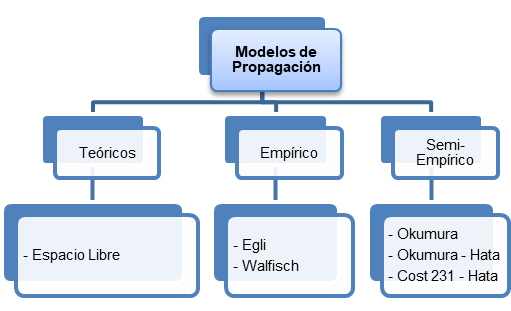
El modelo matemático adaptado de pérdidas de trayectoria se obtiene a partir de los modelos de propagación existentes, los cuales se ajustan intencionalmente a las mediciones obtenidas. En la figura 2 se observa la clasificación de los modelos de propagación considerados (Saunders, 2007).
Las mediciones se realizaron en el campo, registrándose tres valores de la potencia recibida en cada ubicación: potencia mínima, potencia máxima y potencia promedio. Se observó que la potencia recibida en los puntos de medición depende en gran medida, además de la distancia, de las obstrucciones presentes en el enlace entre el transmisor y el receptor.
Como ejemplo, en la Tabla 4 se presentan los valores medidos de la potencia media recibida en los puntos de medición a la frecuencia de 944 MHz, esta tabla se obtiene de una parte de todas las mediciones realizadas.
En la figura 3 se gráfica la potencia media recibida en función del logaritmo de la distancia.
Con los valores medidos de la potencia media recibida se calcularon las pérdidas de trayectoria L, utilizando la siguiente ecuación:
Donde PTx y PRx representan la potencia real de transmisión y la potencia real de recepción, GTx y GRx representan las ganancias de transmisión y recepción respectivamente.
Con los resultados obtenidos, a continuación se procede a determinar el modelo de pérdidas de trayectoria Logaritmo-Distancia, que se expresa de la siguiente manera:
Donde d0 es la distancia de referencia de 1 metro, n es el exponente de pérdida de trayectoria,
Tabla 4. Potencia recibida a 944 MHz en [dBm]
| Puntos | Azimut | Distancia | ||||
|---|---|---|---|---|---|---|
| 70 m | 140 m | 210 m | 280 m | 350 m | ||
| 1 | 0 | -42,52 | -47,69 | -57,87 | -64,92 | Fuera de cobertura |
| 2 | 15 | -44,11 | -55,37 | -56,99 | Fuera de cobertura | Fuera de cobertura |
| 3 | 30 | -45,2 | -55,19 | -61,26 | Fuera de cobertura | Fuera de cobertura |
| 4 | 45 | -46,63 | -51,18 | -60,97 | Fuera de cobertura | Fuera de cobertura |
| 5 | 60 | -46,22 | -51,31 | -61,68 | Fuera de cobertura | Fuera de cobertura |
| 6 | 75 | -43,39 | -64,78 | -68,79 | -68,5 | Fuera de cobertura |
| 7 | 90 | -46,81 | -54,48 | -69,38 | -63,72 | -61,86 |
| 8 | 105 | -47,77 | -52,33 | -57,14 | -57,7 | -57,32 |
| 9 | 120 | -52,73 | -59,89 | -60,14 | -62,03 | -64,33 |
| 10 | 135 | -41,79 | -48,89 | -57,38 | -56,8 | Fuera de cobertura |
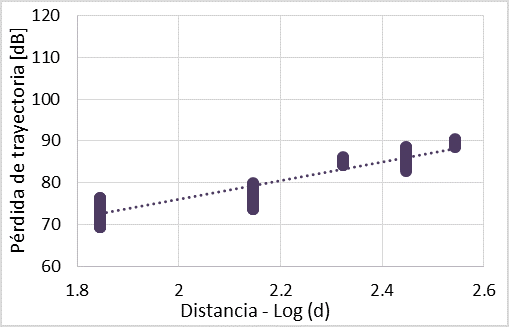
El modelo de pérdidas Logaritmo-Distancia permite establecer una línea de tendencia de regresión lineal que relaciona las pérdidas de trayectoria con la distancia. Los valores de los coeficientes 10n y
En la Figura 4 se aprecian las mediciones obtenidas en las ubicaciones y la recta de regresión lineal obtenida.
En este trabajo se propone adaptar los modelos de propagación existentes a las mediciones mediante el método de ajuste del Error Cuadrático Medio (MSE). Este método permite obtener un valor numérico de ajuste para alcanzar el menor error posible entre dos valores. La ecuación del Error Cuadrático Medio (MSE) es la siguiente:
Donde Lm es el valor medio de las pérdidas de trayectoria obtenido de las mediciones, Lp es el valor de pérdidas de trayectoria calculados con los modelos de propagación existentes y q es el número de puntos de medición.
El valor de ajuste se aumenta o disminuye a la ecuación de pérdidas de trayectoria de los modelos de propagación existentes para adaptarlos a las mediciones.
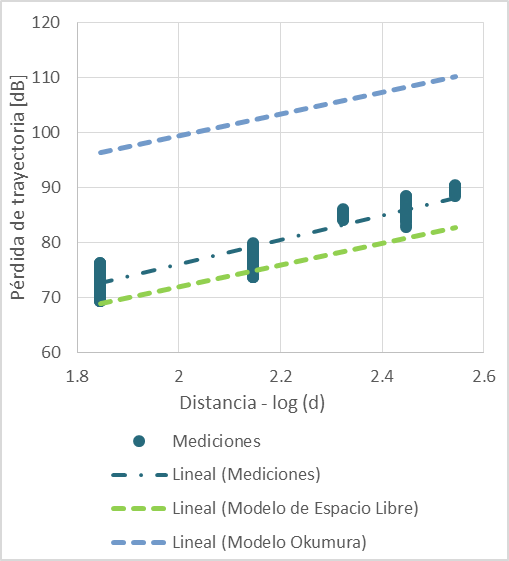
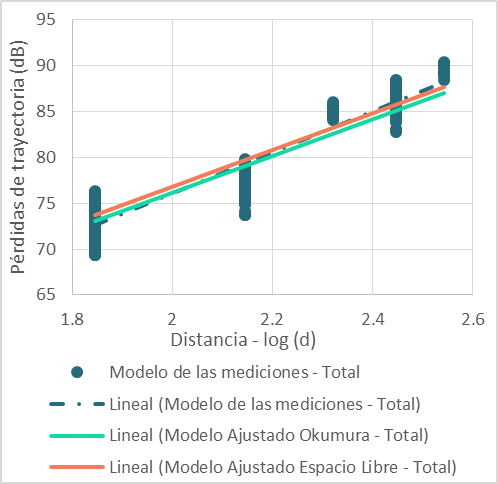
En la Figura 5 se observan las líneas de tendencia de las mediciones para enlaces con línea de vista y de los modelos de propagación de Okumura y Espacio Libre sin ajuste.
En la Figura 6 en cambio se aprecian los modelos de propagación después del ajuste con el Método MSE.
Para enlaces sin línea de vista los modelos de propagación se adaptaron a las mediciones con el método de ajuste simple. La ecuación de ajuste simple es la siguiente:
Este valor de ajuste, al igual que en el método MSE, se aumenta o disminuye a la ecuación de pérdidas de trayectoria de los modelos de propagación existentes.
En la Figura 7 se visualizan las pérdidas de trayectoria obtenidas con los modelos existentes ajustados para enlaces sin línea de vista en escenarios con obstrucción por árboles.Figura 6
Para enlaces sin línea de vista en un escenario con obstrucción por edifícios, los modelos de pérdidas de trayectoria se ajustan de acuerdo a lo que se muestra en la Figura 8.
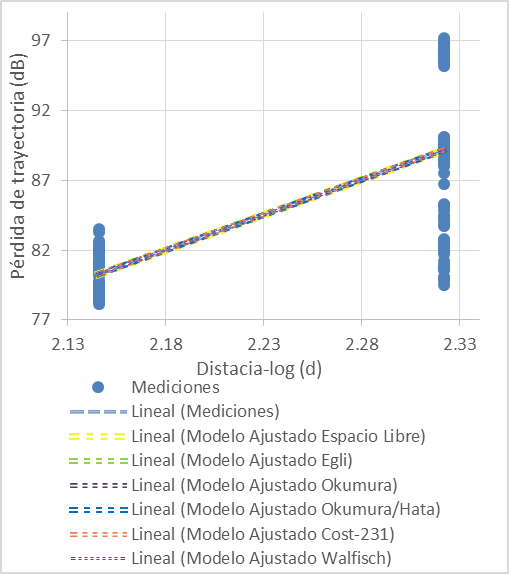
Figura 7. Modelos ajustados de pérdidas de trayectoria con el método simple en escenarios sin línea de vista por árboles.
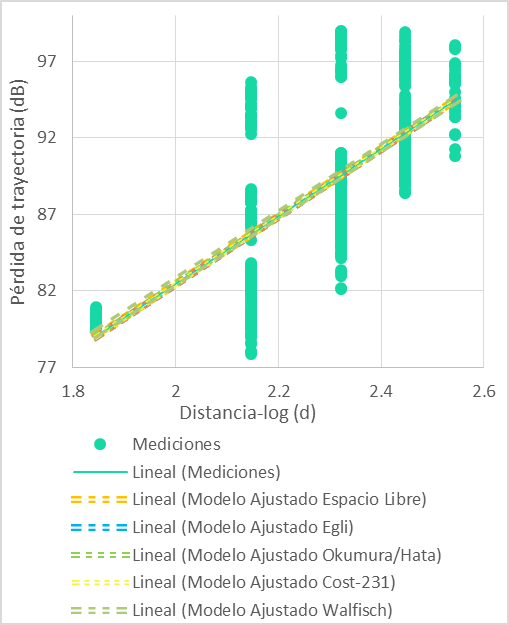
Figura 8. Modelos ajustados de pérdidas de trayectoria con el método simple en escenarios sin línea de vista por edificios.
En la Tabla 5 se incluyen las ecuaciones obtenidas de los modelos adaptados de pérdidas de trayectoria obtenidas con el método de ajuste MSE. Mientras que en la Tabla 6 se encuentran los modelos adaptados con el método de ajuste simple. En las expresiones adaptadas las distancias se indican en metros, ya que la cobertura de las microceldas es menor a los kilómetros.
Tabla 5. Ecuaciones de los modelos adaptados obtenidas con el método MSE
| Modelos de Propagación | Modelo Adaptado para escenarios con línea de vista |
|---|---|
| Espacio Libre |
|
| Okumura |
|
| Modelos de Propagación | Modelo Adaptado para escenarios sin línea de vista obstrucción por edificios |
| Espacio Libre |
|
| Okumura |
|
| Walfisch |
|
| Modelos de Propagación | Modelo Adaptado para escenarios sin línea de vista obstrucción por árboles |
| Egli |
|
| Okumura / Hata |
|
| Cost -231 |
|
Tabla 6. Ecuaciones de los modelos adaptados obtenidas con el método simple
| Modelos de Propagación | Modelo Adaptado para escenarios con línea de vista |
|---|---|
| Espacio Libre |
|
| Egli |
|
| Okumura |
|
| Okumura / Hata |
|
| Cost -231 |
|
| Walfisch |
|
| Modelo de Propagación | Modelo Adaptado para escenarios sin línea de vista con obstrucción por árboles |
| Espacio Libre |
|
| Egli |
|
| Okumura |
|
| Okumura / Hata |
|
| Cost -231 |
|
| Walfisch |
|
| Modelo de Propagación | Modelo Adaptado para escenarios sin línea de vista con obstrucción por edificios |
| Espacio Libre |
|
| Egli |
|
| Okumura |
|
| Okumura / Hata |
|
| Cost -231 |
|
| Walfisch |
|
5. ANÁLISIS DE ERROR DE LOS MODELOS ADAPTADOS
Para comprobar si las ecuaciones de los modelos adaptados de pérdidas de trayectoria se ajustan a las mediciones obtenidas, en la Tabla 7 se realiza un análisis de la exactitud del ajuste mediante el contraste de regresión (F1,n-(k+1)) y el coeficiente de determinación (R2).
De los resultados se observa que la utilización del método de ajuste del Error Cuadrático Medio (MSE) permite obtener modelos aceptables cuando se lo aplica para los enlaces de transmisión con línea de vista, ya que en este escenario se obtienen modelos adaptados de pérdidas de trayectoria con valores promedio de contraste de regresión de 2609,851 y coeficiente de determinación de 0,85.
El método de ajuste simple permite obtener modelos adaptados aceptables para todos los escenarios de aplicación.
Tabla 7. Contraste de regresión y coeficiente de determinación de los modelos adaptados
| Modelos de Propagación para escenarios con línea de vista | Método MSE | Método simple | ||
|
|
|
|
|
|
| Espacio Libre | 2554,53 | 0,847 | 1,09x10^11 | 0,999 |
| Egli | No se aplica | 6,88x10^10 | 0,999 | |
| Okumura | 2665,17 | 0,853 | 1,23x10^11 | 0,999 |
| Okumura / Hata | No se aplica | 1,79x10^9 | 0,999 | |
| Cost-231 | No se aplica | 1,22x10^11 | 0,999 | |
| Walfisch | No se aplica | 1187164,46 | 0,999 | |
| Modelos de Propagación para escenarios sin línea de vista obstrucción por edificios | Método MSE | Método simple | ||
|
|
|
|
|
|
| Espacio Libre | 393,696 | 0,413 | 9,31x10^10 | 0,999 |
| Egli | No se aplica | 1,03x10^11 | 0,999 | |
| Okumura | 391,095 | 0,412 | 1,02x10^11 | 0,999 |
| Okumura/Hata | No se aplica | 1,69x10^9 | 0,999 | |
| Cost-231 | No se aplica | 1,16x10^11 | 0,999 | |
| Walfisch | 634,827 | 0,532 | 55202,158 | 0,999 |
| Modelos de Propagación para escenarios sin línea de vista obstrucción por árboles | Método MSE | Método simple | ||
|
|
|
|
|
|
| Espacio Libre | No se aplica | 3,58x10^10 | 0,999 | |
| Egli | 393,696 | 0,413 | 3,83x10^10 | 0,999 |
| Okumura | No se aplica | 3,82x10^10 | 0,999 | |
| Okumura/Hata | 391,095 | 0,412 | 6,62 x10^8 | 0,999 |
| Cost-231 | 634,827 | 0,532 | 4,63x10^10 | 0,999 |
| Walfisch | No se aplica | 137606,8 | 0,999 | |
6. CONCLUSIONES
Las mediciones efectuadas en la zona de cobertura mostraron que se requiere un ajuste a los modelos de propagación conocidos.
En este proyecto el ajuste de los modelos de propagación se realizó mediante el método del Error Cuadrático Medio y el ajuste simple.
Del presente proyecto se han obtenido modelos de propagación adaptados que pueden ser utilizados como referencia para el diseño de microceldas en la banda de 900 MHz en entornos urbanos de la ciudad de Quito considerando condiciones similares a las establecidas en las mediciones que se efectuaron.