Introducción
La adquisición de conocimientos matemáticos es una preocupación nacional y mundial. Para el 2017, Ecuador intervino en la implementación de PISA para el Desarrollo (PISA-D), a la que asistieron más de 6.100 estudiantes de todo el país. Los resultados de esta prueba matemática son preocupantes, ya que el 70% de los educandos no cumplen con los objetivos planteados en esta área (Instituto Nacional de Evaluación Educativa, 2018).
De acuerdo con el informe de la UNESCO (2019) los estudiantes de diferentes países enfrentan desafíos al trabajar con operaciones que implican fracciones. Incluso en naciones como China y Japón, donde los estudiantes tienen una sólida comprensión conceptual de las matemáticas, las fracciones resultan ser un tema difícil y complejo debido a su naturaleza operativa y la tendencia a olvidar los algoritmos necesarios para su desarrollo.
Es así que se han evidenciado diversas dificultades en el aprendizaje de números fraccionarios, que surgen en torno al desconocimiento de métodos didácticos específicos en el área de matemáticas, los mismos que desmotivan el aprendizaje y el cumplimiento de competencias matemáticas enfocadas en los números racionales.
En base a la temática se han realizado investigaciones previas que se orientan desde la conceptualización de un método matemático denominado método Singapur, que trabaja con tres fases, transformando el aprendizaje de las matemáticas en conceptos visuales, reflexivos y decisivos, así como significativos; de hecho, la importancia de planificar en base a una metodología activa, brinda la oportunidad de trabajar con actividades y recursos interactivos que motivan a los estudiantes.
1.1 Método Singapur
Uno de los elementos que compone la didáctica es la parte metodológica, la misma que al ser propuesta tiene como objetivo desarrollar la comprensión, asimilación y gusto por el aprendizaje. Actualmente este aspecto educativo, bajo el modelo constructivista, dicta ir más allá de la memorización y conceptualización a crear espacios propios de conocimiento y pensamiento. Esta idea se relaciona con lo que Mera (2021) explica sobre el diseño del método Singapur, dando la noción de que “los procesos son conocimientos implicados en la adquisición e implementación de comprensión y están incluidos elementos como razonar, comunicar y hacer conexiones, aplicar y modelar”. (p.11)
El enfoque metodológico que propone el método Singapur se define en 3 fases que constan de una etapa de observación y manipulación con material, concreta; de representa gráficamente o resolver con ayudas visuales los problemas matemáticos, pictórica; y, finalmente, lo abstracto, cuando el niño sitúa símbolos o signos matemáticos que en conjunto con lo anterior puede resolver e integrar fases en su razonamiento.
1.1.1. Enfoque CPA (concreto, pictórico y abstracto)
Con el enfoque CPA los estudiantes construyen sus conocimientos a través de tres niveles de representación graduados por su complejidad: concreto, pictórico y abstracto. En el nivel concreto los estudiantes comienzan a comprender un concepto manipulando materiales y objetos del entorno; en el nivel pictórico avanzan en la comprensión del concepto representándolo mediante dibujos o imágenes; y en el nivel abstracto acaban el proceso de comprensión representándolo mediante signos o símbolos matemáticos (Zapatera, 2020, p.266).
- Concreto: introducción a los conceptos matemáticos mediante la manipulación de materiales y objetos tangibles del entorno. - Pictórica: comprensión de los conceptos matemáticos a través de representaciones visuales, como dibujos o fotografías. - Abstracta: comprender y aplicar algoritmos para resolver problemas matemáticos.
De esta manera, el descubrimiento incentiva el aprendizaje significativo, lo que se traduce como el significado que resulta de la interacción entre el estudiante y el contenido de los aprendizajes. Es entonces cuando deja claro la posición del docente dentro de esta teoría: de guía y orientador. Dicho de otro modo, la función con la que el docente trabaja se entrelaza con el enfoque CPA al plantear un nuevo tema, basándose no solo en un conocimiento previo, sino en la forma en cómo utiliza, esquematiza e interpreta las ideas.
En efecto, dicho enfoque propone trabajar progresivamente a favor de fases que estimulen la manipulación de materiales, uniendo la parte sensoriomotora; esquemas visuales, emergiendo representaciones internas o mentales; que luego será conceptos abstractos, o lo que es lo mismo, una noción propia que puede asociarse con la resolución de problemas más complejos.
1.1.2. Beneficios de aplicar el método Singapur en el aula
Desde el punto de vista de Alba y García (2019):
Al utilizar el método Singapur en clase, el alumno puede adquirir conocimientos no de forma abstracta, sino desde una perspectiva concreta y pictórica. De esta manera, el alumno comprenderá los conceptos y resolverá problemas matemáticos. El método se basa en el uso de material concreto, modelos visuales y práctica constante, todo lo cual ayuda a lograr una comprensión profunda de los conceptos y desarrollar el pensamiento lógico y la creatividad matemática. (p.31)
Dicho de otra forma, la implementación del método Singapur dentro del aprendizaje de números fraccionarios permite crear experiencias concretas y vivenciales, que contribuyen relacionar el entorno cotidiano y la matemática, resultando en el desarrollo y potencialización de las habilidades lógicas, críticas y constructivas, así como de un aprendizaje significativo. En efecto, el docente al fomentar el uso de recursos dentro del aula hace que el estudiante se integre en la elaboración o manipulación de su propio material, posibilitando de este modo un entorno agradable y motivador, igual que un aprendizaje significativo. Puesto que, al participar dinámicamente y dando sentido al material concreto, se construye un pensamiento propio que retroalimenta el aprendizaje adquirido.
1.2 Números fraccionarios
Las fracciones se han reconocido como un componente fundamental y desafiante en la educación matemática, ya que abarcan varios niveles educativos y desempeñan un papel esencial en la resolución de situaciones cotidianas. Además, el conocimiento de fracciones promueve el razonamiento y el pensamiento crítico de las personas.
Para representar una fracción se utilizan dos números dispuestos en una línea horizontal. El numerador se coloca en la parte superior de la línea, mientras que el denominador se sitúa debajo de la línea.
Según Crespo (2022):
Para la resolución de problemas de fracciones es algo fundamental el uso de representaciones, que harán al alumnado comprender de una forma mucho más clara, qué es lo que tienen que realizar en cada caso. Para que esto sea eficaz se trabaja representando todo aquello que el problema nos dice mediante barras. (p.34)
En resumen, es fundamental utilizar gráficos para representar fracciones, ya que esto permite visualizar patrones, tendencias, relaciones y estructuras de los datos. Esta representación no solo ayuda al estudiante a comprender conceptualmente la información, sino también a comprenderla de forma visual.
1.2.1 Enseñanza de fracciones
Muchos estudiantes, en su escolaridad, se ven expuestos a diferentes retos, los cuales suelen tornarse de gran dificultad, como, por ejemplo, el tema de las fracciones, cuyos conceptos básicos respecto al tema no se consolidan de manera adecuada en cada uno de ellos. Dado que, muchos estudiantes ven a las fracciones como símbolos sin sentido o miran el numerador y denominador como números separados, en lugar de comprenderlos como un todo unificado. Por ello, a continuación, se observa la importancia del trabajo manipulativo, pictórico y abstracto dentro de este tema; para lograr en los educandos un conocimiento significativo en su aprendizaje.
1.2.1.1 Trabajo manipulativo
Teniendo en cuenta la variedad de metodologías y técnicas de enseñanza y aprendizaje a la hora de afianzar este tipo de conocimientos, como docentes se debe buscar diferentes alternativas para enseñar fracciones de una manera fácil y divertida.
Al respecto, Castañeda (2021) menciona que:
Las actividades que se proponen con material concreto e imágenes, relacionan las fracciones con una experiencia visual e invita al estudiante a apropiarse del objeto mental fracción y sus operaciones multiplicación y división, para luego introducir reglas y símbolos que 19 tengan sentido, de modo que poco a poco van a adquirir herramientas para desarrollar la capacidad de analizar y construir soluciones a diversas actividades (p. 18).
Por lo tanto, la forma más efectiva de enseñar las fracciones es utilizando materiales manipulativos y concretos. Al trabajar de esta manera con fracciones y sus equivalencias en porcentajes y decimales, los niños pueden descubrir las propiedades de las fracciones, desarrollar interés por las matemáticas y disfrutar del aprendizaje. Además, esta metodología les brinda la oportunidad de fortalecer su autoestima y fomentar la autonomía en el aprendizaje.
1.2.1.2 Trabajo pictórico
Es importante que los niños tengan acceso a materiales pictóricos antes de abordar las fracciones escritas. Esto significa que pueden utilizar estos materiales en juegos que involucren multiplicaciones y divisiones.
Como señala Ramos (2021) para poder avanzar en la adquisición de diferentes conceptos relacionados con las fracciones, es necesario comprender de una forma correcta el término de fracciones equivalentes. Esto servirá tanto para entender que las fracciones representan una cantidad, como para operar con ellas
En este sentido, para que esta percepción sea comprendida en su totalidad se debe realizar a través de la representación, intentando que sea completamente entendida, y no solo realizar varias acciones mecánicamente.
1.2.1.3 Trabajo abstracto
Es fundamental tener en consideración que los niños de 9 a 10 años se encuentran en la etapa de operaciones concretas, en la cual están adquiriendo estructuras lógico-matemáticas. Este aspecto permite reconocer la capacidad de los estudiantes para establecer relaciones entre actividades, extraer conclusiones a partir de diferentes ejercicios y abordar la interpretación y resolución de problemas que puedan surgir en situaciones reales.
Dentro de la metodología Singapur, se le otorga una gran importancia a la resolución de problemas. “En Singapur se limitan los procedimientos rutinarios, poniendo mucho más énfasis en la resolución de problemas” (Ramos, 2019, p. 98). Por tanto, en el marco de la educación básica, se enfoca en trabajar con operaciones simples, con el objetivo de fomentar la comprensión y resolución de problemas.
Metodología
2.1. Tipo de investigación
El objetivo de esta investigación es proponer la aplicación del método Singapur como estrategia determinante para el aprendizaje de números fraccionarios en alumnos de educación general básica. Este trabajo se basa en una investigación descriptiva con enfoque cualitativo, lo que implica utilizar criterios sistemáticos para obtener datos y estructuras que caractericen la realidad investigada. Se detallarán las utilidades y características de la aplicación del método, especialmente en la comprensión de números fraccionarios y su adaptación en el aula de clases para el desarrollo efectivo de habilidades y destrezas lógico-matemáticas.
2.2 Método
Esta investigación se basa en un enfoque deductivo, respaldado por la afirmación de Prieto (2018) quien sostiene que este construye sus fundamentos sobre ciertos fundamentos teóricos hasta configurar hechos o prácticas concretas, por tanto, se utiliza este método para llegar a conclusiones basadas en juicios previamente identificados, facilitando así la interpretación y comprensión profunda de la información recolectada sobre el tema en cuestión.
2.3 Técnica de la investigación
La investigación se apoya en estudios de carácter documental, lo que implica recopilar información a partir de la compilación de documentos y fuentes secundarias. Los datos obtenidos se extrajeron de investigaciones previas, lo que permitió realizar análisis y representaciones gráficas mediante tablas y figuras. La investigación se respalda en diversos repositorios y bases de datos académicos, como Dianet y Google Scholar, entre otros.
Resultados
En los datos recopilados en la base de datos PISA (2018) se puede observar el avance de aprendizaje de los estudiantes a nivel mundial, en los resultados se evidencia que los educandos no poseen estrategias lúdicas suficientes para el logro de competencias matemáticas en el sistema educativo latinoamericano. Sin embargo, se toma en consideración la aplicación del método Singapur, ya que obedece a un currículum que permite el progreso con respecto a sus habilidades, enfocándose principalmente en la resolución correcta de problemas matemáticos, promoviendo de esta forma el desarrollo del pensamiento.
Por su lado, Castillo (2022) comenta que el método Singapur es eficaz para el proceso de enseñanza-aprendizaje en la asignatura de Matemáticas, pues se dirige especialmente en la resolución de las cuatro operaciones básicas.
Además, Salazar (2021) señala en su estudio que la enseñanza de las fracciones requiere la inclusión de actividades variadas con métodos y técnicas flexibles de enseñanza-aprendizaje. Es importante utilizar material didáctico que facilite y fomente la comprensión y aplicación de los números racionales en situaciones prácticas.
Mientras que Parra (2020) menciona que el método Singapur se basa en comprender el texto leído, el conocimiento claro deseado, organizar la información gráficamente o representarla con objetos para encontrar la respuesta correcta mirando o tocando las partes de la tarea. Así mismo, hace referencia que estimular visualmente al estudiante hace que comprenda el proceso de ejercicios básicos que se plantean, de tal forma que por medio de ello se puede aplicar a acciones específicas y relacionar con las matemáticas.
3.1. Comparación de resultados
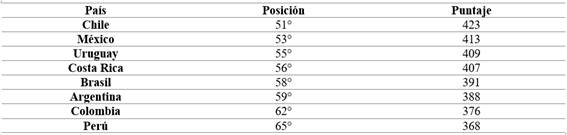
En cuanto a los resultados ejecutados por las pruebas PISA (2018), como se muestra en la Tabla 1, se pudo observar que:
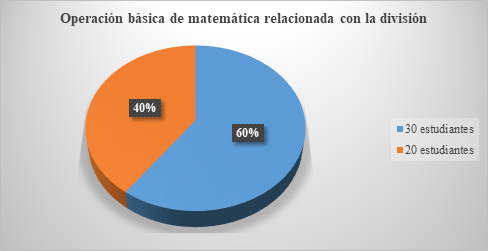
Por otro lado, en la Figura 1 se muestran los resultados obtenidos en la investigación de Castillo (2022).
En este sentido, de acuerdo con los datos reflejados en la Tabla 1, se revela que la educación en América Latina, en 2018 está por debajo del estándar promedio, pues se evidencia en el examen realizado por la Organización para la Cooperación y el Desarrollo Económico (OCDE), ninguno de los estudiantes logra obtener una puntuación de al menos 494 puntos en Matemáticas; sin embargo, en la Figura 1 se pudo denotar que en el año 2022 de igual forma se refleja un bajo desempeño en cuanto a la solución de ejercicios fraccionarios, se muestra que la mayoría de estudiantes no alcanzan un nivel óptimo de aprendizaje. En síntesis, la enseñanza-aprendizaje de los números fraccionarios o divisiones no ha tenido una mejora en los últimos años.
Los datos recopilados en la encuesta aplicada a estudiantes en el estudio de Salazar (2021) se encuentra representada en la Tabla 2.
Tabla 2 En relación a la Enseñanza de Números Fraccionarios, ¿Qué Tipo de Recursos Educativos Emplea el Profesor para Impartir una Clase sobre Fracciones?
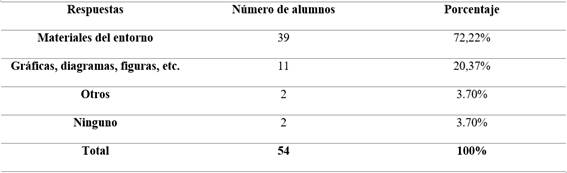
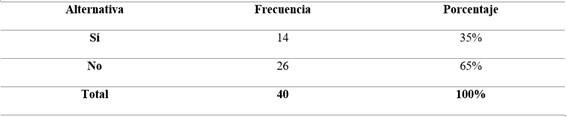
No obstante, Parra (2020) en su trabajo de investigación pudo denotar lo siguiente que se evidencia en la Tabla 3.
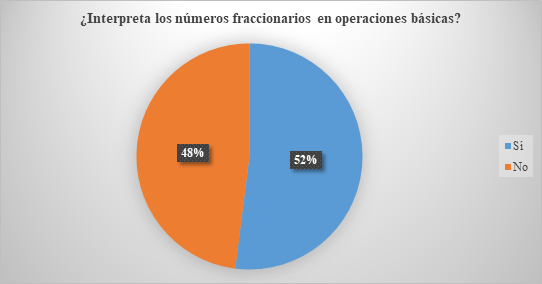
Por otra parte, se considera la investigación de Castillo (2022) donde se incluye la encuesta realizada a los estudiantes que está representada en la Figura 2.
En relación a los datos expuestos, se pudo apreciar en la Tabla 2 que los docentes usualmente utilizan materiales del entorno y la representación gráfica de figuras, barras, entre otros, para la enseñanza-aprendizaje de los números fraccionarios; no obstante, en la Tabla 3 se menciona que un gran porcentaje de los educadores no utilizan gráficos para añadir elementos a una operación; finalmente, en la Figura 2 se denota la poca interpretación y comprensión de los números fraccionarios en las operaciones básicas. En síntesis, el poco uso tanto de material concreto, como la representación gráfica de las operaciones, dificulta a los estudiantes la resolución e interpretación de resultados.
3.2 Interpretación de resultados
Los datos obtenidos por las pruebas PISA reflejan un bajo desempeño en cuanto a los dominios básicos en Matemática, ya que ninguno de los países estudiados alcanza los 494 puntos para Matemática; esto se ve complementado con los resultados arrojados por otro estudio, en donde se reflejó que un 72.22 % de los docentes utilizan materiales del entorno para la enseñanza-aprendizaje de los números fraccionarios, mientras que tan solo un 20.37% maneja la representación gráfica de las operaciones, esto se relaciona con los niveles de conocimiento lógico-matemático, puesto que se demostró que un 60% de los estudiantes no obtienen un aprendizaje significativo, esto debido al escaso uso de material concreto que los docentes deberían utilizar a la hora de enseñar dichas nociones básicas, es así que al aplicar el método Singapur el estudiante desarrolla un aprendizaje lógico de manera que establece las 3 fases para la construcción de estos conocimientos, los cuales son: concreto, pictórico y abstracto.
Para finalizar, cabe destacar que el 65% de los docentes no hace uso de gráficos para añadir elementos a una operación, esto se relaciona con que el 48% de los estudiantes no interpreta los números fraccionarios en operaciones básicas, así pues, la mayor parte de estudiantes no son capaces de interpretar dichas cantidades, y, de igual forma, se hace notoria por parte del docente que no está estimulando visualmente al niño para que pueda comprender el proceso y así aplicarlo en operaciones concretas. En este sentido, se puede decir que los docentes no aplican diversas metodologías que ayuden a la enseñanza del estudiante. A pesar de ello, se denotó que al aplicar el método Singapur un 52% si logra interpretar los números fraccionarios, por lo tanto, al aplicarlo se lograría que el estudiante sepa interpretar correctamente los números fraccionarios en operaciones básicas, desarrollando sus estímulos, los cuales permite que pueda observar, ver, entender, analizar y responder aplicando los diferentes procedimientos algorítmicos para resolver los ejercicios de las fracciones.
Se concluye así, que para que el estudiante se apropie de un pensamiento abstracto, debe ser participe activo al momento de interpretar los procedimientos ante la resolución de problemas matemáticos. Y eso es lo que brinda el método Singapur, al permitir que los estudiantes expliquen los procedimientos e incluyan dichas nociones matemáticas en sus palabras.
Conclusiones
Dentro de los puntos destacables del trabajo, y, en función del objetivo general, mismo que presenta la intención de determinar la incidencia del método Singapur en el aprendizaje de números fraccionarios en los alumnos de educación general básica, se concluye que para lograr que el método Singapur tenga valor y alcance su objetivo, es imprescindible observar y considerar tanto los ritmos de aprendizaje de los estudiantes durante la clase, como la complejidad del tema al proponer una metodología; en otras palabras, para que el estudiante comprenda conceptos abstractos, como en el caso de los números fraccionarios, es esencial trabajar desde su razonamiento e interpretación; es decir, que sea él quien organice y contextualice conceptos matemáticos yendo más allá de la parte teórica.
Lo dicho anteriormente se traduce a cómo utilizar, de acuerdo con las fases del método, recursos visuales que asocien y orienten a la resolución de problemas cotidianos, de forma que desarrollen competencias y habilidades lógicas-matemáticas con una motivación propia.
La clave del método Singapur, centrado en el área de matemáticas, es cambiar la perspectiva tradicionalista por un método que concrete temas familiarizados al contexto o entorno cotidiano del niño; lo que incluye materiales y actividades que aprendan haciendo. Del mismo modo se exponen varios de los beneficios que brinda este método en la adquisición de conocimientos con respecto al aprendizaje de números fraccionarios, como, por ejemplo, permite relacionar los problemas y operaciones matemáticas en la utilización de materiales manipulables lo que incluye una visión realista al uso de las matemáticas y su simbología en la vida diaria, resultado así en la adquisición y desarrollo de habilidades y destrezas críticas.
Tras observar los resultados del estudio se determina que el nivel de conocimiento de los estudiantes al aplicar el método Singapur es favorable, pues se denota la factibilidad de aprender de manera activa, y, a través de las distintas fases, qué contiene el método. En cuanto al contenido relacionado con las fracciones, deja en evidencia que los estudiantes mejoran su comprensión al representar de forma gráfica, como algebraica, los problemas matemáticos. Además, se destaca la participación y el nivel de motivación de los estudiantes durante las clases de Matemáticas, lo que induce una señal positiva del interés por aprender e interactuar con el material.
Finalmente, como estrategia concreta, el método Singapur favorece a la construcción de conocimientos que se adquieren durante el proceso de enseñanza, pues mediante un conjunto de actividades se fomenta un pensamiento propio, ya que cuando el estudiante manipula, representa y finalmente conceptualiza las nociones matemáticas, refleja ser un método eficiente que abarca la exploración y las experiencias en un participativo escenario educativo. De hecho, implementar este método en el área de matemáticas implica organizar un ambiente de autoconfianza, comunicación, participación e incluso trabajo colaborativo. En este sentido se evidencia un aprendizaje constructivo, cuyo beneficiario es el niño y su aporte brinda habilidades, actitudes y motivación que superan la idea de que la matemática es compleja a una que es interactiva y flexible.