Introducción
La tecnología ha sido indispensable para los procesos de enseñanza y aprendizaje durante los dos últimos años (2020 y 2021), debido a la pandemia causada por el COVID-19; de esta forma, muchas escuelas utilizaron plataformas educativas para darle continuidad a la educación de sus ciudadanos; bajo esta circunstancia, las aplicaciones y recursos educativos virtuales se convirtieron en plataformas indispensables para todos los docentes y sus estudiantes, “puesto que admiten complementar los procesos educativos desde el indagar saberes previos, desarrollar temáticas de forma más lúdica, buscar información de manera más rápida, simular laboratorios e incluso evaluar a través de diferentes métodos” (Barrios et al., 2021, p.52).
La enseñanza de las matemáticas también se vio involucrada con el uso frecuente de las herramientas tecnológicas, apoyándose en instrumentos virtuales como GeoGebra, el cual es definido por Rodríguez et al. (2021) como un asistente matemático que ofrece muchas ventajas desde sus funciones, ya que es portable y de libre acceso. Asimismo, GeoGebra favorece la enseñanza y el aprendizaje matemático y geométrico si se usa adecuadamente con los alumnos (Jaraba, 2020). Por otra parte, existen otras aplicaciones virtuales comunes para la enseñanza de las matemáticas cómo: La red Educativa Digital Descartes, la web Geometría dinámica y aplicaciones móviles (Geometrix, Fórmulas geométricas, Artric, entre otras).
Pese a estas plataformas, un recurso que se ha consolidado en los últimos años ha sido la realidad aumentada (RA), cuyo propósito está centrado en la creación de contenidos virtuales en un espacio real, el cual también incentiva a la creatividad y la motivación por aprender por parte de los estudiantes, ya que “su versatilidad, transversalidad y fácil manejo hacen que el usuario se sienta cómodo durante el proceso de aprendizaje” (De La Horra, 2017).
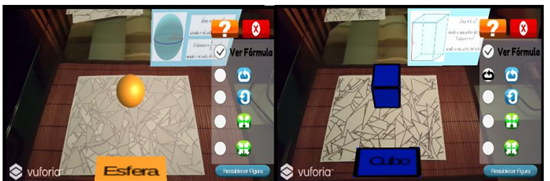
Desde las matemáticas, la aplicación de la realidad aumentada puede ser benéfica para el desarrollo del pensamiento geométrico variacional, ya que investigaciones como la de Arellano y Villanueva (2018) resaltan que la aplicación de esta herramienta es útil y tiene un impacto positivo en el interés del alumno; además, Gómez et al. (2018) exponen que la conexión con la geometría es inmediata al utilizar RA, existiendo una manipulación natural de los conceptos geométricos y sobre todo, la manipulación de los modelos tridimensiones. Con base en lo anterior, cabe resaltar que el funcionamiento de la realidad aumentada necesita la utilización de un dispositivo móvil (celular o tablet, por ejemplo), para que a través de su cámara se puedan situar objetos virtuales en el espacio real, tal como se muestra en la Figura 1, lo que Moreno y Pérez (2017) complementan al afirmar que “es un sistema que aporta información virtual, sea en formato de texto, imagen, audio, vídeo y modelos 3D, al entorno espacio-temporal donde se encuentra el usuario de la aplicación” (p.45).
La RA posee algunos niveles de aplicación, los cuales según Gómez et al. (2018), basados en Lens-Fitzgerald, fundador de Layar (navegador de realidad aumentada apta para dispositivos Android), son: nivel 0, hiperlanzando el mundo físico, donde se obtienen imágenes a través de códigos QR o imágenes en 2D en tiempo real; nivel 1, RA basada en marcadores, donde se reconocen patrones en 2D y 3D fijando la realidad virtual; nivel 2, RA sin marcadores, basado en GPS, brújulas e imágenes reales; nivel 3, visión aumentada, es la realidad aumentada inmersiva, donde se necesitan cascos y gafas de RA. Con base en lo anterior, los niveles usados con mayor frecuencia en las escuelas son del 0 al 2, ya que el nivel 3 requiere de equipos más sofisticados.
Para la enseñanza y aprendizaje de las matemáticas con alumnos de educación media (10mo grado) en Colombia, se ha venido utilizando por algunos docentes la realidad aumentada en sus niveles 0 y 1; sin embargo, según expresan Martínez et al. (2021), su incorporación debe tener una intencionalidad pedagógica bien definida, debido a que el uso de recursos tecnológicos no garantiza el aprendizaje. Además, “la realidad aumentada permite desarrollar competencias que son necesarias para el aprendizaje del álgebra y permite mejorar la visualización de las figuras con las cuales los estudiantes interactuarán” (González et al., 2021, p. 541).
En este orden de ideas, es necesario preguntarse ¿cómo ha sido el efecto del uso de la realidad aumentada en el desarrollo del pensamiento geométrico variacional en estudiantes de bachillerato? Por tanto, se realizó una investigación exploratoria que conllevó a este artículo, cuyo objetivo fue analizar el efecto de la aplicación de la realidad aumentada como instrumento para el desarrollo del pensamiento geométrico variacional, en estudiantes de bachillerato en Colombia.
Metodología
La investigación se desarrolló desde un enfoque cualitativo, debido a que se hizo necesario comprender e interpretar los sucesos en el aula; además, según Sambrano (2020), este enfoque busca “la subjetividad, la multiplicidad de interpretaciones de una realidad y un gran sentido común, con enorme capacidad de escucha y sin juicios previos, involucra conocimientos provenientes de las fuentes más diversas” (p.26). De acuerdo a lo mencionado, se analizaron las diversas respuestas de los estudiantes a tres actividades relacionados con el pensamiento geométrico variacional al implementar GeoGebra Calculadora 3D.
Con respecto a las actividades abordadas, cabe resaltar que cada una tuvo un nivel de complejidad, por lo que el proceso de análisis tomó en cuenta las dificultades y fortalezas que mostraron los alumnos para dar respuesta a las preguntas o indicaciones. Además, se consideraron las percepciones de los alumnos en relación con la aplicación de la realidad aumentada para su aprendizaje geométrico.
2.1 Sujetos de estudio
Esta investigación se llevó a cabo en el Colegio Seminario Conciliar San Luis Beltrán de la ciudad de Barranquilla, Colombia, donde se trabajó con un total de 16 estudiantes entre las edades de 14 a 16 años, pertenecientes a educación media en el décimo grado, para la implementación piloto de la actividad con RA. Los alumnos fueron organizados en grupos de trabajos conformados por cuatro miembros para llevar a cabo las diferentes actividades aplicando GeoGebra Calculadora 3D. Posteriormente se seleccionaron cuatro de estos 16 estudiantes para aplicar una entrevista destinada a describir sus percepciones del desarrollo e implementación de las actividades con RA.
2.2 Método de trabajo
Para las actividades relacionadas con el desarrollo del pensamiento geométrico variacional se empleó la observación participante, la cual es definida por Campos y Lule (2012) como aquella donde “el investigador se involucra dentro de los procesos de quienes observa, y éste es plenamente aceptado, por lo tanto, se estima que lo observado no se ve afectado por la acción del observador” (p.53).
La forma de trabajo fue la siguiente: los cuatro grupos conformados por los estudiantes del grado décimo desarrollaron dos sesiones de clases divididas de la siguiente manera:
Acercamiento a las herramientas y manera de utilización de la aplicación GeoGebra Calculadora 3D, posteriormente a esto, aplicación de la actividad inicial (Tabla 1), toma de evidencias y discusiones;
Realización de la actividad intermedia y de cierre (Tabla 2 y 3), toma de evidencias y socialización de las respuestas. Una vez realizadas las actividades mencionadas anteriormente, se aplicó un instrumento de investigación para recoger las percepciones de los alumnos en relación con la utilización de la realidad aumentada en sus procesos educativos.
2.3 Instrumento aplicado
Para la recolección de la información relacionada con las percepciones de los alumnos basado en el desarrollo del pensamiento geométrico variacional, se aplicó una entrevista semiestructurada, la cual según Ñaupas et al. (2018) se caracteriza por no ser tan rígida, lo que permite al investigador hacer otras preguntas con el fin de aclarar información o hacer que el entrevistado retome el tema si se desvía del mismo.
La entrevista estuvo conformada por tres preguntas (ver Figura 2) y se aplicó a cinco estudiantes que estuvieron dispuestos a participar de la misma; las respuestas ofrecidas por ellos fueron gradabas en audio y posteriormente transcritas de forma literal para la realización del análisis a través de una reducción fenomenológica.
Resultados
3.1 Observación del uso de GeoGebra Calculadora 3D por parte de los alumnos
La primera actividad (Tabla 1) tuvo como fin observar el uso adecuado de GeoGebra Calculadora 3D por parte de los alumnos; es decir, conocer si el estudiante es capaz de ubicar puntos en un espacio virtual, conectarlos con segmentos y formar adecuadamente un sólido geométrico. De la misma forma, esta actividad permitió analizar si el alumno puede corregir con facilidad sus errores y ser consciente cuando los comete; asimismo, realizar procesos de identificación y operacionalización de variables como áreas y volúmenes.
Durante el desarrollo de esta actividad se logró observar un mayor interés por aprender, los alumnos mostraron afinidad con la asignatura y discutían de manera grupal la mejor estrategia para elaborar el sólido geométrico propuesto en la Actividad 1, lo que concuerda con Gómez et al. (2018), quienes exponen que la aplicación de la RA mejora la conexión de los estudiantes con la geometría. Por otra parte, esta actividad inicial resultó satisfactoria, observándose algunos aspectos cómo: 1) el trabajo en equipo, 2) la corrección de errores de manera instantánea, 3) la manipulación inmediata de las herramientas virtuales, 4) el cálculo de variables como longitudes, áreas y volúmenes aplicados y, 5) la observación y análisis de la figura 3D desde diversas perspectivas.
Sumando a lo anterior, la Actividad 1 mantuvo a los alumnos en constante movimiento, explorando figuras geométricas virtuales en un espacio real; es decir, se trasladaban en el salón de clase observando a través de la cámara de su dispositivo el espacio (
En la Tabla 2 se expone la actividad intermedia relacionada con el pensamiento geométrico variacional, en ella, los alumnos debían conocer las pautas para ubicar puntos en el espacio y también ser diestros en el trazo de rectas o funciones lineales en GeoGebra Calculadora 3D. Asimismo, debían aplicar principios para calcular áreas y volúmenes teniendo en cuenta variables como alturas, bases y profundidad del sólido creado.
Cabe resaltar que los alumnos en esta actividad realizaron cálculos manuales de manera inicial, para luego comparar sus resultados con los arrojados por el programa, algunos grupos tuvieron que realizar consultas como el área de un triángulo, volumen de una pirámide, entre otros conceptos; lo que evidenció una debilidad conceptual sobre esta temática estudiada desde el año anterior, según el programa oficial de matemática.
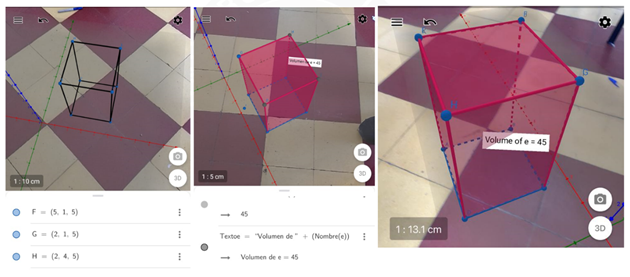
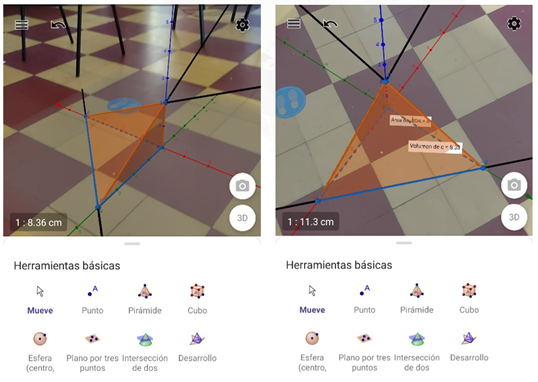
La aplicación de la Actividad 2 mostró la forma espontánea de los alumnos en manipular las herramientas virtuales, ubicando los elementos geométricos de manera más rápida. Algunos estudiantes manifestaron que no era necesario guiarlos en el proceso, ya que sabían cómo representar los puntos, las rectas, el área y el volumen del sólido. Evidentemente el interés por aprender no disminuyó, por el contrario, los alumnos realizaron la actividad en un tiempo menor al planificado, lo que concuerda con González et al. (2021) cuando expresan que la RA permite comprender mejor el álgebra y visualizar las figuras geométricas con mayor destreza, interactuado fácilmente con estas. En la Figura 4 se muestran los resultados de la Actividad 2, evidencias del trabajo de un grupo de alumnos.
La actividad de cierre (Tabla 3), exigió que los alumnos fueran capaces de manipular variables haciendo consideraciones pertinentes para poder resolver el problema; es decir, requirió pensar en una estrategia donde tomen valores arbitrarios (sea para el radio o la altura) y poder crear un sólido que cumpla con las condiciones dadas. Esta actividad se consideró enriquecedora debido a los diversos resultados que se pueden obtener y se permite el dialogo entre pares para comparar sus sólidos o buscar una manera diferente se resolverla, considerando también el hecho de calcular el volumen de un cilindro para este caso.
En esta actividad los alumnos iniciaron ubicando elementos básicos en el espacio, cómo: puntos, radios, circunferencias y cilindros de manera arbitraria, posteriormente explicaron el proceso que realizaron para llegar a una solución. Un ejemplo de lo anterior es la respuesta de un grupo de alumnos, quienes explicaron paso a paso su proceso antes de determinar las medidas de las dimensiones pedidas: “Iniciamos creando un círculo con centro en (0,0,0) y consideramos un radio de 3 unidades, luego hicimos un cilindro encima del círculo y pusimos una altura de 4 unidades. Después de eso, aplicamos la herramienta volumen sobre la figura y nos dimos cuenta que el volumen era menor a 200, por lo que empezamos a mover el punto de la altura hasta llegar al volumen de 200. Nos vimos cuenta que la medida del volumen no caía en el valor de 200 exactamente, sino que estaba aproximado, nos daba 198,89 o 200,55”
Con lo anterior, se logró observar que, al no tener medidas específicas, los estudiantes procedían a utilizar figuras de manera arbitrarias para luego mover el punto del radio o de la altura hasta llegar al volumen de 200
Asimismo, los grupos manipularon la figura para poder obtener medidas aproximadas en el cilindro; con base en esto, otro grupo concluyó que: “las medidas de las dimensiones necesarias para 200
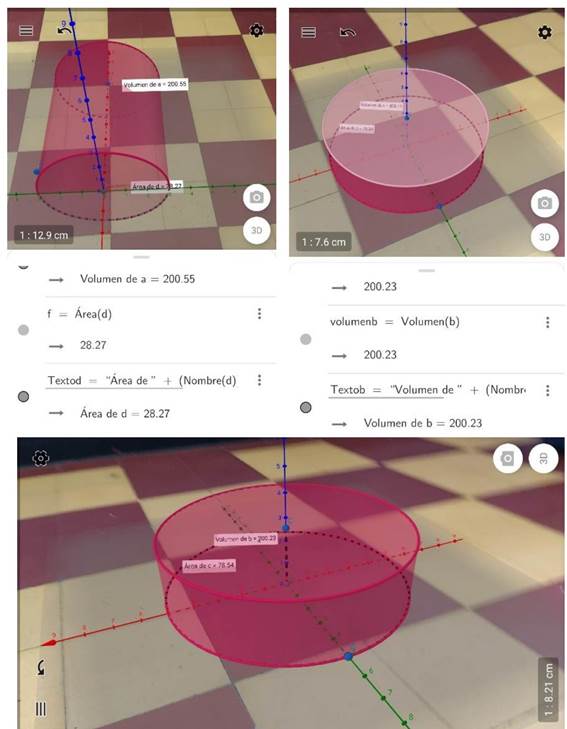
Estas medidas fueron comparadas entre los equipos, quienes mostraron a los demás las figuras realizadas por ellos y analizaron que la estructura del sólido puede cambiar dependiendo de las variables consideradas desde el inicio. A continuación, en la Figura 5 se observan algunos ejemplos realizados de la actividad final.
Una vez finalizadas las tres actividades se procedió a aplicar la entrevista semiestructura a 4 estudiantes seleccionados, tomando uno de cada grupo conformado. Para la organización de los datos se grabaron las respuestas y luego a transcribieron. A continuación, se presentan los resultados obtenidos.
3.2 Resultados de la entrevista
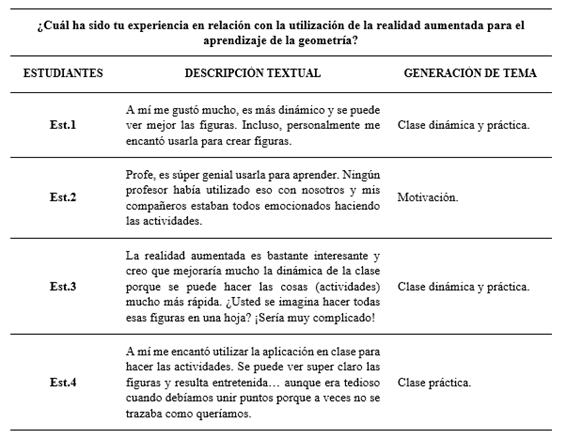
El análisis de la información recolectada de la entrevista semiestructura se realizó a través de una reducción fenomenológica, la cual según Castillo (2021), ayudan a entender nuestros supuestos, creencias y conocimientos sobre un fenómeno o determinadas experiencias. A continuación, en la Tabla 4 se exponen las diferentes respuestas adquiridas en cada una de las preguntas.
Dentro de las respuestas obtenidas por los cuatro estudiantes entrevistados, las cuales fueron transcritas textualmente en la tabla 4, se evidencia varias ideas puntuales, pero la que toma mayor fuerza y resalta en todo momento es la palabra “práctica”. Esto hace énfasis a la idea de que las matemáticas pueden entrelazar los procesos abstractos con actividades que logran abordar la practicidad de los conceptos, lo cual es la esencia del desarrollo matemático. Por esto, la RA contribuye enormemente al desarrollo de una clase práctica, porque busca que el estudiante potencialice la intuición interactuando con un fenómeno o un concepto de estudio (Gómez et al., 2018).
Otras apreciaciones de los estudiantes se refieren a que el uso de este tipo de herramientas genera un alto impacto en la motivación para desarrollar las actividades en clase (o incluso fuera de ella) y que ineludiblemente el quehacer matemático se vuelve más dinámico, lo que ayudaría a una excelente metodología educativa, lo que trae como consecuencia la adquisición de un aprendizaje significativo; y es que, “la motivación y el aprendizaje son dos de los pilares fundamentales sobre los que se crean las metodologías. Es por ello, que la realidad aumentada dota del medio para conseguir este fin” (De La Horra, 2017, p.9).
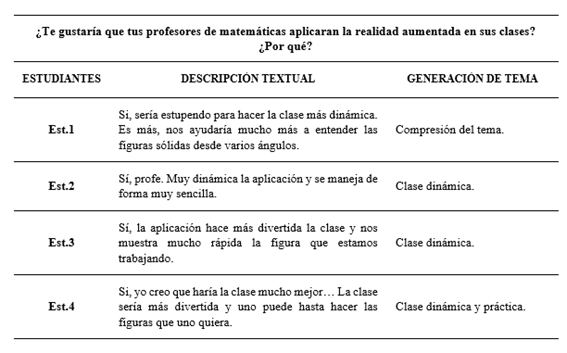
Como se evidencia en la Tabla 5, las respuestas aportadas por los cuatro estudiantes evidencian el gran interés y gusto que tienen estos en relación con el uso de herramientas virtuales en las clases de matemáticas, y en específico, el uso de la realidad aumentada en la geometría y, basándose en las respuestas obtenidas por ellos, las clases serán mucha más dinámica y práctica.
Estas dos ideas son predominantes en la entrevista, siendo respuestas comunes en la pregunta 1 y 2, lo que lleva a inferir que en la educación matemática esta predominando una clase magistral en la que el estudiante no se involucra dinámicamente en la construcción del aprendizaje y, por ende, no hay una comprensión total de los conceptos desarrollados, esto concuerda con González et al. (2021), donde exponen que el uso de la realidad aumentada ayuda positivamente a desarrollar competencias que son necesarias para el aprendizaje y que desde las asignaturas como el álgebra y la geometría, se puede experimentar con figuras y variables no abstractas, sino visibles, creando una interactividad con estos elementos de manera inmediata.
Al preguntarle a los estudiantes cual fue la actividad que más les gusto, varios de estos coinciden que la primera actividad (Tabla 6), esto es debido a que les incentivó la curiosidad y las ganas de aprender por medio de acciones prácticas que los mantuvieron motivados, lo que fue un agente activo dentro del proceso enseñanza - aprendizaje, creando a su vez un dinamismo en la clase y permitiendo que estos estuviesen más interesados en la clase, perdiendo también esa apatía hacia esta disciplina. Este resultado coincide con los de Gómez et al. (2020), quienes afirman que: “en definitiva, la Realidad Aumentada es un recurso emergente que puede constituir una mejora motivacional en el estudiantado” (p. 44).
Asimismo, los estudiantes manifestaron de igual forma que les gustó la actividad 2 y 3 porque les ayudó a afianzar los conceptos de área y volumen de sólidos y comprenderlos mejor, lo cual está vinculado al objetivo de la clase: llegar a la comprensión del concepto estudiado. Este resultado concuerda con el obtenido por Saldivia et al. (2018), quienes concluyeron que: “se puede favorecer la comprensión del espacio tridimensional al permitir interactuar de otra manera con los conceptos al asociarlos a objetos cotidianos, facilitando así la interpretación geométrica de los mismos y complementando el trabajo algebraico que se realiza usualmente” (p. 318)
Conclusiones
En esta investigación se analizó el efecto del uso de la realidad aumentada en el desarrollo del pensamiento geométrico variacional en estudiantes de bachillerato, evidenciando que los estudiantes asocian el uso de esta herramienta con la palabra clase dinámica, lo que genera en ellos una motivación y disposición para el desarrollo de tal evento académico. Además, se logra comprender que la RA va más allá de una clase dinámica, puesto que lo alumnos generan un vínculo entre la teoría y la práctica, visualizando conceptos abstractos a través de objetos virtuales incrustados en un espacio real (ver Figuras 4, 5 y 6), despertando la motivación y la curiosidad.
La RA generó un efecto positivo hacia el desarrollo pedagógico en el proceso de enseñanza - aprendizaje, se observó que la actividad inicial tuvo mayor impacto en relación con las otras actividades, debido a que los alumnos pudieron desarrollar con mayor eficacia los métodos básicos que ayudaron al dominio de las herramientas de la aplicación GeoGebra Calculadora 3D. Por lo que en la actividad inicial se logró despertar la motivación y la participación activa, esto es consecuente con el hecho de que “los estudiantes muy motivados suelen participar de forma activa y espontánea en las actividades y encuentran agradable el proceso de aprendizaje sin esperar recompensas externas” (Castillo et al., 2022, pp.9)
Por último, se recomienda seguir realizando más investigaciones sobre este tema, con el fin de profundizar sobre los efectos del uso de la realidad aumentada en el desarrollo del pensamiento geométrico variacional u otras formas de pensamiento, abordando diferentes niveles educativos y buscando ampliar mucho más la visión de la RA en la educación matemática.