Introducción
La información de los resultados académicos de los estudiantes tradicionalmente ha sido analizada al finalizar el período escolar y ha sido útil para generar estadísticas y reportes históricos (Illescas et al., 2018), más no para tomar decisiones inmediatas que se dan durante el curso de los estudios, y que permitan optimizar el proceso de aprendizaje, por eso, el objetivo de la investigación es analizar las calificaciones de los estudiantes y presentar la información mediante gráficas de las trayectorias de sus estudios, estas gráficas facilitan a las autoridades académicas visualizar los datos apenas estos sean ingresados al sistema informático y puedan tomarse decisiones que permitan realizar intervenciones a estudiantes o cursos que tengan dificultades con su rendimiento académico.
Este documento presenta inicialmente los fundamentos teóricos sobre las clases de matemáticas en el bachillerato ecuatoriano, el rendimiento académico (Villarreal et al., 2009), y la visualización de las trayectorias escolares, luego se describe la metodología basada en el análisis de calificaciones y la generación de gráficas de trayectorias escolares para la presentación de los datos. Finalmente se presentan los resultados con el análisis de las calificaciones y de la presentación mediante gráficas de trayectorias de los estudiantes de la institución educativa investigada.
1. Dificultades en el aprendizaje de matemáticas
La matemática es una asignatura que los estudiantes encuentran difícil porque los temas están encadenados y la complejidad cada vez se incrementa, la materia, en ciertos casos, se vuelve abstracta. No todos los docentes dominan aspectos didácticos, ni tienen la facilidad para desarrollar estos temas (Bravo et al., 2017); además, aunque el modelo para la educación ecuatoriana sea el constructivista, el docente todavía tiene por prioridad el cumplir con la planificación, antes que velar por el logro de aprendizajes de los estudiantes (Bravo, 2020), estas carencias que tiene el docente influyen en las dificultades que tiene el estudiante en su aprendizaje de la asignatura.
El alumno tiene la motivación para aprender y el docente debe aprovechar esa disposición para conseguir esos aprendizajes (Gonzáles, 2015); sin embargo, no todos los profesores lo logran y muchos estudiantes tienen dificultades con la asignatura, no le ven la utilidad para su vida, no se adaptan al régimen escolar ni a las metodologías de los docentes (Pacheco & Narváez, 2015), y finalmente se produce el efecto contrario: tienen temor y aversión a las matemáticas, y cuando la actitud es negativa, el rendimiento es bajo (Mato & De la Torre, 2009). Por lo anterior, es frecuente que los estudiantes tengan bajos rendimientos en la materia caso de estudio y los factores que lo explican pueden ser múltiples: personales, familiares, educativos (Gonzáles, 2015), otros factores, como la pobreza y la marginación que son razones que también pueden incidir en su rendimiento (Velasco, 2016). Es de suma importancia que los docentes desarrollen la matemática siempre ligada a las aplicaciones prácticas, a ejemplos del contexto, para que los estudiantes se motiven y encuentren significatividad a sus aprendizajes.
Para lograr un adecuado rendimiento, se requiere que el estudiante encuentre a través de la materia respuestas a sus problemas del diario vivir, el conocer que la asignatura tiene un sentido práctico lo motiva a aprender (Bravo et al., 2017), es el docente quien debe orientar a que el estudiante se cuestione, reflexione y desarrolle su mente (Gonzáles, 2015), también este es quién debe identificar de forma temprana cualquier problema del estudiante o del grupo, para que se implementen programas de intervención con fines preventivos (Lamas, 2015). El docente suele identificar las dificultades individuales, pero no siempre a las del grupo, y eso impide que reflexione sobre su práctica educativa y adopte estrategias que le permitan adoptar correctivos.
En el proceso de aprendizaje del estudiante intervienen tres grandes factores: aptitud, instrucción y ambiente (Fajardo et al., 2017), que explican en gran medida el aprendizaje, pero la forma común de medir el grado de apropiación de los conocimientos está dado por las calificaciones escolares, que, aunque se expresan de forma cuantitativa, nos permiten comprenderlo (Rea, 2018), pese a esto, existen críticas por lo subjetiva que pueda ser esta medida y por las diferentes formas de evaluar que se habrán dado para obtenerlas (Lamana & De la Peña, 2018). Todavía es común que se piense que la nota sirve exclusivamente para decidir la promoción del estudiante al siguiente nivel (Trelles et al., 2017). La educación ecuatoriana prevé diversos componentes de evaluación para la obtención la calificación del estudiante.
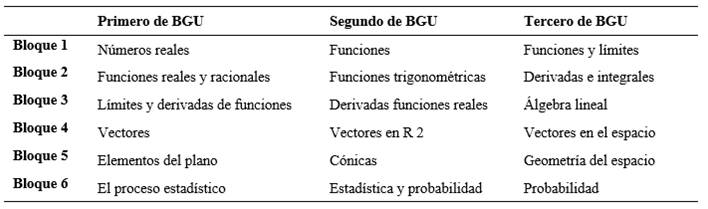
En el bachillerato, la asignatura de matemáticas adquiere relevancia, haciendo hincapié en la modelación y en las aplicaciones contextualizadas (Educación, 2016a). Para cada año de bachillerato se abordan seis bloques o unidades temáticas, para primero (Educación, 2016b), segundo (Educación, 2016c), y tercero de bachillerato (Educación, 2016d), cuyo detalle lo podemos observar en la Tabla 1.
Los docentes deben evaluar el logro de destrezas en cada bloque con una serie de actividades individuales y grupales, además de la presentación de tareas y lecciones, así como las pruebas que conforman la calificación del bloque. Esta gran cantidad de componentes de evaluación de cada bloque ofrece mucha información que es útil para determinar cómo transcurre el proceso de logro de destrezas por parte de los estudiantes.
Toda la actividad académica que se genera en el aula, durante el período escolar, puede tener dificultades, ya sea para un estudiante en particular, para un grupo, o para un docente, la clave de esto es poder identificar esa dificultad a tiempo para poder responder de forma inmediata, con acciones académicas que mejoren la situación.
2. Gráficas de trayectorias escolares
Se puede seguir el desempeño de un estudiante y de su curso a través de las trayectorias escolares, estas describen el avance en los estudios de los alumnos durante un período académico. Se revisaron investigaciones previas que analizan las trayectorias de los estudiantes, algunas lo hacen en función del abandono que ocasionan los bajos rendimientos (Terigi, 2007), o del plazo en que se finalizan los estudios; en ambos casos debe esperarse al final de un proceso para tomar decisiones, y esos datos sirven como información histórica (Illescas et al., 2018), pero son importantes otras formas de analizar el rendimiento, como las calificaciones que se obtienen en un curso y que pueden dar cuenta del desarrollo del proceso formativo (Lamas, 2015). Si las notas son analizadas durante ese proceso mismo, pueden ser útiles para la toma inmediata de ciertas decisiones de tipo académicas.
La presentación de las calificaciones de los estudiantes mediante gráficos facilitan la interpretación y el análisis de la información (Peña et al., 2019), para la generación de gráficos se utilizan coordenadas paralelas, metodología que permite mostrar datos de múltiples variables en un solo gráfico multidimensional (Baldino et al., 2016; Keim, 2002), estos gráficos muestran la secuencia de temas que se han ido desarrollando y los rendimientos académicos de cada estudiante y del grupo (Bravo, 2019). La generación de gráficos mediante coordenadas paralelas posibilitan el procesamiento de datos complejos y en grandes cantidades (Heinrich & Weiskopf, 2013; Gómez et al., 2014). Se ha adoptado esta metodología, que permite la presentación de gráficos de trayectorias escolares, que son simples de interpretar, y muestran las calificaciones obtenidas por cada estudiante en los diferentes temas desarrollados en el año escolar.
Metodología
La investigación propone una metodología donde se pueda observar de forma gráfica las trayectorias escolares de los estudiantes de bachillerato, para esto se procesan grandes cantidades de datos académicos, calificaciones para generar las gráficas, esta presentación de forma visual facilita identificar cualquier problema en algún tema, o dificultad de algún estudiante y la consecuente toma de decisiones académicas de forma oportuna.
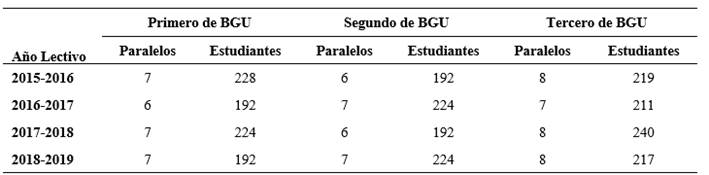
Como evidencia de la versatilidad de la propuesta metodológica se presenta el análisis de las calificaciones y la visualización de las trayectorias escolares de los estudiantes de los tres años de bachillerato en la asignatura de matemática. Se generaron gráficas de los 84 paralelos que se abrieron entre septiembre del 2015, hasta junio del 2019, de primero, segundo y tercer año de bachillerato de la Unidad Educativa La Asunción de Cuenca, Ecuador, información que está en la Tabla 2.
En la investigación fue proporcionada la base de datos académica que posee la institución educativa, donde constan datos generales y la información académica de los estudiantes, se trabaja con los rendimientos académicos en la asignatura matemática. De cada una de los 84 grupos fue factible procesar las calificaciones y generar gráficas de los diferentes componentes que se evalúan en la educación ecuatoriana: tarea autónoma individual (TAI), actividad individual en clase (AIC), actividad grupal en clase (AGC), lección individual (LEC), evaluación sumativa (SUM), promedio (PROM) y refuerzo (REF), dando la posibilidad de realizar un análisis con mayor detalle.
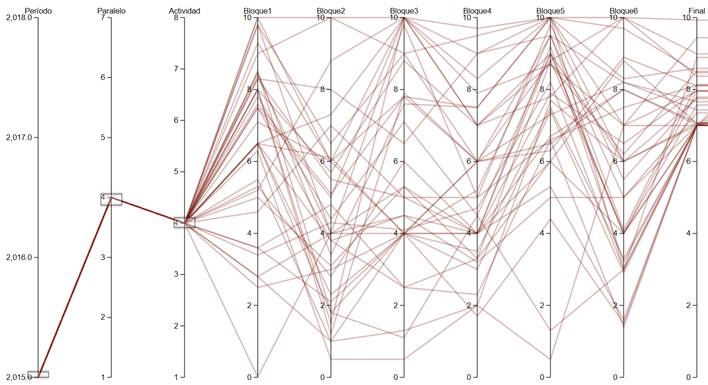
Para la visualización se utiliza la librería d3.js para codificar la forma en que se presenta la información académica al usuario. La presentación gráfica, permite al usuario seleccionar el año, el curso y el componente evaluado. En la Figura 1 se pueden observar líneas de trayectoria, cada una representa a un estudiante, esa línea muestra las calificaciones obtenidas en cada bloque que el estudiante ha cursado durante el año escolar, se puede identificar alguna dificultad de un estudiante cuando las calificaciones de este son bajas en todos los bloques. El conjunto de líneas de trayectoria muestra el comportamiento de un curso completo, allí es posible evidenciar las calificaciones de todo el grupo en cada bloque, también es fácil identificar la trayectoria de cada estudiante y sus calificaciones en cada bloque.
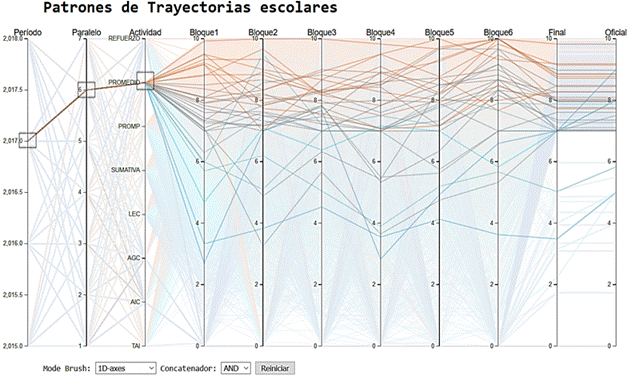
Figura 1 Promedios en los 6 bloques de matemática de los estudiantes del primero de bachillerato del paralelo 6 del año lectivo 2017-2018.
La visualización es muy versátil, permite graficar líneas de trayectorias de diferentes años, para poder comparar entre diferentes promociones; también, se pueden generar las gráficos de trayectoria de cada uno de los cursos (paralelos) que funcionan simultáneamente, otra característica de la visualización es que se pueden observar los diferentes componentes de la evaluación que rigen en la educación ecuatoriana, como: trabajo autónomo individual, actividades individuales en clase, actividades grupales en clase, lección individual, evaluación sumativa, y promedio.
La información que proporcionan las gráficas de trayectoria escolar, es corroborada con el análisis cuantitativo de las calificaciones, de esta forma se visibilizan temáticas difíciles, componentes de la evaluación donde las calificaciones del todo un curso son bajas, además se pueden identificar casos individuales de estudiantes que tienen bajos rendimientos académicos, todo esto con el fin de tomar decisiones inmediatas.
Resultados
Se trabajó en la generación las gráficas de trayectorias de los estudiantes en matemáticas, las gráficas presentan las calificaciones obtenidas por ellos en cada bloque, pudiéndose escoger la visualización de cada uno de los diferentes componentes de la evaluación para lograr un análisis más detallado.

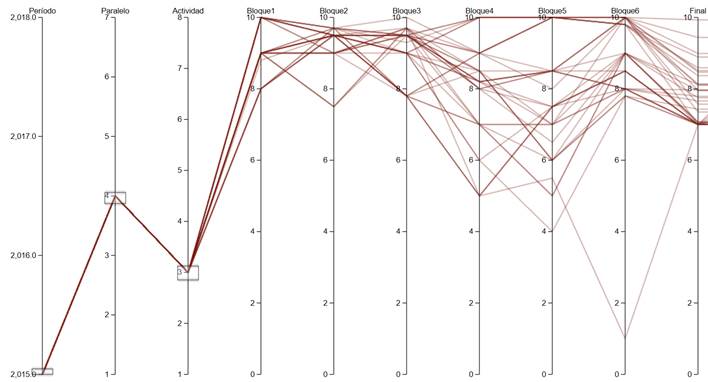
Figura 2 Rendimiento académico de los estudiantes del paralelo 8 del tercero de bachillerato del año lectivo 2017-2018.
Como ejemplo, en la Figura 2 se muestra la gráfica de trayectorias escolares del paralelo 6 del primero de bachillerato del año 2017-2018, se visualizan los promedios en cada bloque. Cada línea corresponde a la trayectoria escolar de un estudiante, donde se representan las calificaciones en cada uno de los seis bloques de estudio. En la misma gráfica se puede observar el comportamiento de todos los demás estudiantes del mismo curso y tener una idea global de sus calificaciones. Se observa la trayectoria de ciertos estudiantes con calificaciones inferiores a siete en algunos bloques.
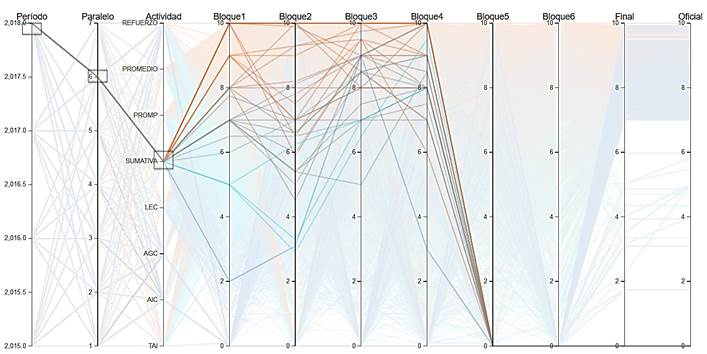
Figura 3 Dificultades grupales o individuales en el bloque 2 de los estudiantes de primero de bachillerato de año lectivo 2018-2019.
La Figura 3 corresponde a estudiantes del paralelo 6 del primero de bachillerato del año 2018-2019, allí se puede identificar los diferentes bloques donde el rendimiento es malo y verificar si las bajas notas son grupales o individuales, de modo que las autoridades académicas puedan tomar decisiones inmediatas, ya sea de una intervención colectiva para reforzar ciertas destrezas complejas vistas en un bloque, o de una intervención individual para el apoyo a un estudiante que lo requiera. Este gráfico fue capturado cuando se registraba un avance de la asignatura hasta el cuarto bloque, todavía no se habían cursado los demás bloques.
Lo observado se refuerza con el análisis cuantitativo de las notas: el bloque 1 de Números reales, con una media de 7,81 puntos y desviación estándar de 1,8 puntos; el bloque 2 de Funciones reales y Racionales, con 7,18 puntos de media y 2,05 puntos de desviación estándar con el más bajo promedio y alta dispersión; el tercer bloque de Límites de funciones con 8,54 puntos de media y 1,19 puntos de desviación estándar; y el cuarto bloque de Vectores con 8,51 puntos de media y 1,43 puntos de desviación estándar.
La mayor ventaja de la visualización de trayectorias escolares, es que si la información académica está actualizada por parte del docente, las gráficas de las trayectorias escolares de los estudiantes están disponibles para que los propios docentes o autoridades realicen un seguimiento permanente de los datos presentados de forma visual, y se tomen decisiones inmediatas cuando sean detectadas cualquier tipo de anomalías.
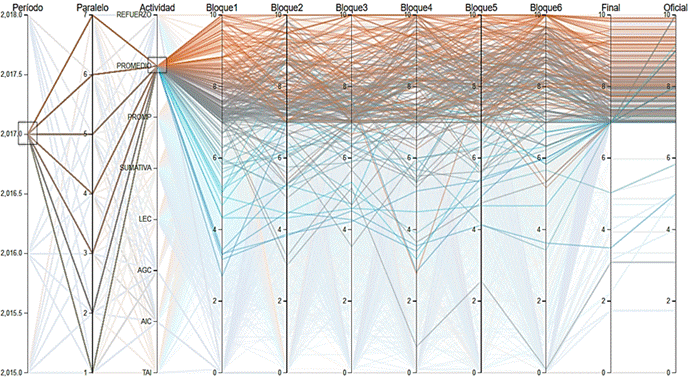
Figura 4 Notas del promedio por bloques donde se evidencia que la mayoría de calificaciones son iguales o superiores a 7.
En la Figura 4 se observa claramente que las calificaciones obtenidas por todos los estudiantes de primero de bachillerato del año 2017-2018, en su mayoría están sobre 7 quedando pocos estudiantes con notas inferiores, esto nos indica que los docentes tienen en cuenta que se debe obtener la nota mínima de 7 para aprobar, si el estudiante obtiene una nota menor es responsabilidad del docente trabajar en la recuperación de ese estudiante.
Dado que es factible graficar cada componente que forma parte de la evaluación, es posible identificar que, en las actividades individuales, se tienen menores calificaciones que en las actividades colaborativas; para evidenciar esto, se presentan dos gráficos del paralelo 4 del primero de bachillerato del año lectivo 2015-2016. Las calificaciones de tipo individual están mostradas en la Figura 5, tienen un promedio de 5,98 puntos y una alta dispersión con una desviación estándar de 2,65 puntos.
Por su parte, las actividades colaborativas mostradas en la figura 6, donde los estudiantes logran calificaciones más altas con 8,28 puntos de media aritmética y una menor dispersión, con una desviación estándar de 1,64 puntos.
La visualización mediante coordenadas paralelas permite identificar las dificultades ya sean personales o grupales. En este proyecto de investigación, una vez que se han detectado los problemas de rendimiento en un bloque, identificará las razones de esa dificultad, diseñará una estrategia de intervención, que, al aplicarse, busca lograr una mejor calidad de los aprendizajes y la consiguiente mejora de los rendimientos académicos.
3. Discusión
Algunos estudios presentan gráficas de la trayectoria escolar (Terigi, 2007) donde se observa la evolución de la cohorte, mostrando cómo avanza la trayectoria del grupo de estudiantes secundarios, cuantificando a aquellos que desertan los que se atrasan, pero siempre mostrando información histórica, a diferencia de la presente investigación, donde se muestra lo que sucede durante el año escolar con el detalle de cada estudiante y en cada bloque de estudio.
En una investigación en Argentina fueron usadas coordenadas paralelas para seguir el progreso de cada estudiante en su carrera universitaria durante cinco años, con el fin de estudiar su evolución y explicar la tasa de egreso, el presente proyecto también usa coordenadas paralelas para presentar información académica individual, pero se hace énfasis en el detalle de lo que sucede en cada tema de estudio de un año escolar de los estudiantes de bachillerato (Díaz y otros, 2015).
En Ecuador se presentaron gráficas de trayectoria, donde se construyó una variable denominada trayectoria que incluía el avance y el rendimiento, haciendo que la línea de trayectoria sea referencial (Illescas et al., 2018). En los tres casos descritos la presentación de datos fue histórica, a diferencia este proyecto que busca que se visualice la información apenas se han cargado las calificaciones de las evaluaciones y poder de esta forma detectar cualquier problema individual o grupal. En este proyecto se presentan gráficos de trayectoria académica, donde la variable es el rendimiento académico, esto permite a la autoridad académica analizar la información de las calificaciones en cada bloque de forma visual y se facilite su identificación.
Mediante coordenadas paralelas se presentaron gráficas de rendimiento académico de estudiantes universitarios, donde se distinguen los rendimientos de los estudiantes en cada período escolar y clasificados por las distintas carreras de la universidad, es allí donde se puede observar las dificultades que atraviesan los estudiantes de las diferentes carreras en el curso de sus estudios; mientras, en este proyecto, con mucho detalle se pueden ver las trayectorias individuales, analizar los diferentes componentes que formaron parte de la evaluación, e identificar aquellos donde se presentan dificultades (Peña et al., 2019).
Conclusiones
Es de gran importancia que se pueda presentar la información académica de forma visual, ya que detrás de estas gráficas de muy simple interpretación, existen grandes cantidades de datos procesados. El análisis de la información presentada, a través de gráficos de trayectorias escolares, puede permitir la detección temprana de problemas de rendimiento académico que facilita la planificación oportuna de cualquier intervención que mejore la calidad de los aprendizajes y los rendimientos académicos.
Fueron fácilmente visualizadas las trayectorias escolares de cada estudiante, de modo que se puede identificar algún estudiante con bajas calificaciones en un bloque, o con bajo rendimiento en todo el año lectivo, información que puede ayudar a que se intervenga de forma oportuna con ese estudiante. También se pueden ver bloques en los que todo un curso tiene dificultades, de modo que se puedan planificar actividades de refuerzo en aquellos temas más complejos. Otra posibilidad es acceder a los registros de los diferentes componentes de la evaluación y determinar en cuáles existen dificultades y buscar estrategias que logren mejoras. Todas estas posibilidades de visualización de las calificaciones, mediante trayectorias escolares, permiten a la autoridad analizar los datos de forma oportuna y tomar inmediatamente decisiones que redundan en que los estudiantes puedan lograr aprendizajes significativos, y a los docentes implementar variantes metodológicas y refuerzos a sus clases.
Una vez aplicada la propuesta de visualización de trayectorias escolares, los beneficiarios directos serían los estudiantes porque mejoran la comprensión de los temas, obtendrían mejores calificaciones y elevarían sus posibilidades de acceder a la educación superior; también para el departamento de matemáticas conformado por todos los docentes del área, porque ellos podrían realizar un análisis exhaustivo de los problemas que puedan presentarse en sus clases de matemáticas; y, para la institución educativa ya que mejoraría sus indicadores de rendimiento académico y la posibilidad de que sus estudiantes logren un cupo para ingresar a la universidad, indicador de logro de gran importancia para la unidad educativa investigada.