Introduction
In this work, we study the approximate controllability of the following system with unbounded delay, non-instantaneous impulse, and non-local condition. To achieve our result we will use a technique developed by A. Bashirov et al.(Bashirov & Ghahramanlou, 2014; Bashirov & Jneid, 2013; Bashirov, Mahmudov, Şemi, & Etikan, 2007), which does not use fixed point theorems as many researchers do. On the other hand, as the delay is infinite, we consider a phase space that satisfies the axiomatic theory propose by Hale-Kato to study retarded differential equations with unbounded delay (Hale & Kato, 1978; Hino, Murakami, & Naito, 2013). These results prove once again that the controllability of a linear system is preserved if we consider the impulses, the non-local conditions and the delays as disturbances of it, which is very natural in real life problems, never the critical points of a differential equation is exactly the critical point of the model that it represents, the same happens with the impulses, the delay and non-local conditions; they are intrinsic phenomena to the real problem, that many times they are not taken into account at the moment of carrying out the mathematical modeling:
where 𝐼 0 = 0, 𝑡 1 , 𝐼 𝑘 = 𝑠 𝑘 , 𝑡 𝑘+1 , 𝐽 𝑘 = 𝑡 𝑘 , 𝑠 𝑘 , 0= 𝑠 0 < 𝑡 1 < 𝑠 1 < 𝑡 2 < 𝑠 2 <⋯< 𝑠 𝑝 < 𝑡 𝑝+1 =𝜏.
There exists a fixed number 𝛱>0 such that 𝜋 𝑞 ≤ min 𝜋,𝜏 , where 0,𝜏 is the maximal interval of local existence of solutions of problem (1.1); and 0≤ 𝜋 1 < 𝜋 2 <…< 𝜋 𝑞 , 𝑖=1,…,𝑞, selected under specific rules marked by the real-life problem that the mathematical model could represent, such as: 𝜋 𝑖 = 𝑖 𝜋 𝑞 𝑝 , 𝑖=1,…, 𝑞. The advantage of using non-local conditions is that measurements at more places can be incorporated to get better models. For more details and physical interpretations see Byszewski & Lakshmikantham (1991), Byszewski (1990), Byszewski (1991), Chabrowski (1984), Vrabie (2015), and references therein. 𝒦: 𝔎 𝑞 →𝔎, 𝜙: ℝ − → ℝ 𝑛 , 𝜙∈𝔎, 𝔎 is the phase space to be specified later. 𝑓: ℝ + ×𝔎× ℝ 𝑚 → ℝ 𝑛 , is a smooth enough function, 𝒢 𝑘 : 𝐽 𝑘 × ℝ 𝑛 → ℝ ?? , 𝑘=1,2,3,⋯,𝑝, are continuous and represents the impulsive effect in the system (1.1), i.e., we are considering that the system can have abrupt changes that stay there for an interval of time. These alterations in state might be due to certain external factors, which cannot be well described by pure ordinary differential equations, (see, for instance, Lakshmikantham, Bainov, & Simeonov (1989) and Selvi & Arjunan (2012) and reference therein). 𝒜 𝑡 ∈ ℝ 𝑛×𝑛 , ℬ 𝑡 ∈ ℝ 𝑛×𝑚 and 𝜙∈𝔎, where 𝔎 is the phase space that will be defined later (see section 2). For this type of problems the phase space for initial functions plays an important role in the study of both qualitative and quantitative theory, for more details, in case without impulses and non-local conditions, we refer to Hale & Kato (1978), Hino et al. (2013) and Shin (1987, 1987). The function 𝑧 ? 𝜃 =𝑧 𝑡+𝜃 for 𝜃∈ −∞,0 illustrate the history of the state up to the time 𝑡, and also remembers much of the historical past of 𝜙, carrying part of the present to the past.
Additionally, we assume the following conditions on the nonlinear term 𝑓
where 𝜁: ℝ + → 0,∞ is a continuous function. In particular, 𝜁 𝜉 =𝑎 𝜉 𝛽 +𝑏, with 𝛽≥1. Associated with the semilinear system (1.1), we also consider the linear system
(1.3) 𝑧 ′ 𝑡 =𝒜 𝑡 𝑧 𝑡 +ℬ 𝑡 𝑢 𝑡 , 𝑡∈ 𝑡 0 ,𝜏 , 𝑧 𝑡 0 = 𝑧 0 .
Also, we shall assume the following hypothesis:
H1) The linear control system (1.3) is exactly controllable on any interval 𝜏−𝛿,𝜏 , for all 𝛿 with 0<𝛿<𝜏.
The hypothesis H1) is satisfied in the case that 𝒜 𝑡 =𝐴 and ℬ 𝑡 =𝐵 are constant matrices since the algebraic Kalman's condition (Lee & Markus, 1986) for exact controllability of linear autonomous systems do not depend on the time interval.
Other examples of time-dependent systems satisfying the hypothesis H1) can be found in Leiva & Zambrano (1999). In addition, there are several papers on the existence of solutions of semilinear evolution equations with impulses, with impulses and bounded delay, with bounded delay and non-local condition, and with non-local conditions and impulses. To mention, one can see Selvi & Arjunan, (2012). Recently, in Abbas, Arifi, Benchohra, & Graef (2020), the existence of periodic mild solution of infinite delay evolution equations with non-instantaneous impulses has been studied by using Koratowski's measure of non-compactness and Sadowski's fixed point theorem. In recently work Ayala-Bolagay, Leiva, & Tallana-Chimarro (2020), using some ideas from the preceding paper and Hale & Kato (1978), Liu (2000), Liu, Naito, & Van Minh (2003), to define a particular phase space 𝔎 satisfying Hale-Kato axiomatic theory, the existence of solutions for this type of systems has been proved applying Karakosta's fixed point theorem, which is an extension of Krasnosel'skii's Fixed Point Theorem for contraction and compact mappings, as in Karakostas (2003), Leiva & Sundar (2017). But, as far as we know, this system's controllability has not been studied before.
Preliminaries
This section is dedicated mainly to select the appropriate phase space 𝔎 to set this problem, which must satisfy the axiomatic theory proposed by Hale and Kato to study differential equations with infinite delay; that on the one hand, on the other hand, we will give a formula for the solutions of the problem posed through the evolution operator or transition matrix corresponding to the associated linear system. To this end, we denote by 𝛷 the fundamental matrix of the linear system
(2.4) 𝑧 ′ 𝑡 =𝒜 𝑡 𝑧 𝑡 , 𝑡∈ℝ
i.e., 𝑑𝛷 𝑡 𝑑𝑡 =𝒜 𝑡 𝛷 𝑡 , 𝛷 0 =𝐼,
then the evolution operator 𝒰 𝑡,𝑠 is defined by 𝒰 𝑡,𝑠 =𝛷 𝑡 𝛷 −1 𝑠 ,𝑡,𝑠∈ℝ. For 𝜏>0, we consider the following bound for the evolution operator
Now, we shall define the space of normalized piecewise continuous function, denoted by 𝒫𝒲=𝒫𝒲( −∞,0]; ℝ 𝑛 , as the set of functions such that their restriction to any interval of the form 𝑎,0 is a piecewise continuous function. i.e.,
Using some ideas from Liu (2000), we consider a function ℎ:ℝ→ ℝ + such that
Remark 2.1. A particular function ℎ is ℎ 𝑠 =exp −𝑎𝑠 with 𝑎>0.
Now, we define the following functions space
In Abbas et al. (2020), Hale & Kato (1978), Liu (2000), Liu et al. (2003), and other references it is mentioned that this space is a Banach space, which certainly it is true because we did the proof.
Lemma 2.2. The space 𝐶 ℎ endowed with the norm
is a Banach space.
Our phase space will be
equipped with the norm
Now, we shall consider the following larger space
From Lemma 2.2, we have the following,
Lemma 2.3. 𝒫𝒲 ℎ𝜏 is a Banach space endowed with the norm 𝑧 = 𝑧 | ℝ − 𝔎 + 𝑧 | 𝐼 ∞ where 𝑧 | 𝐼 ∞ = sup 𝑡∈𝐼= 0,𝜏 𝑧 𝑡 .
For more details about it, one can see Abbas et al. (2020), Hale & Kato (1978), Liu (2000), Liu et al. (2003).
Thus, 𝔎 will be a linear space of functions mapping −∞,0 into ℝ 𝑛 endowed with a norm ∥⋅ ∥ 𝔎 .
Now, let us denote by
i.e.,
and the norm in the space 𝔎 𝑞 is given by
Definition 2.4. (Exact Controllability) The system (1.1) is said to be exactly controllable on 0,𝜏 if for every 𝜙∈𝔎, 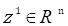 there exists 𝑢∈ 𝐿 2 0,𝜏; ℝ 𝑚 such that the solution 𝑧 𝑡 of (1.1) corresponding to 𝑢 verifies:
there exists 𝑢∈ 𝐿 2 0,𝜏; ℝ 𝑚 such that the solution 𝑧 𝑡 of (1.1) corresponding to 𝑢 verifies:
Definition 2.5. (Approximate Controllability) The system (1.1) is said to be approximately controllable on 0,𝜏 if for every 𝜙∈𝔎, 𝑧 1 ∈ 𝐼?? 𝑛 and 𝜖>0, there exists 𝑢∈ 𝐿 2 0,𝜏 ; ℝ 𝑚 such that the solution 𝑧 𝑡 of (1.1) corresponding to 𝑢 verifies:
Controllability of Linear System
In this section, we shall present some known characterization of the controllability of the linear system (3.5) without impulses, delays, and non-local conditions. To this end, we note that for all 𝑧 0 ∈ 𝐼𝑅 𝑛 and 𝑢∈ 𝐿 2 0,𝜏; ℝ 𝑚 the initial value problem
(3.5) 𝑦 ′ =𝒜 𝑡 𝑦 𝑡 +ℬ 𝑡 𝑢 𝑡 , 𝑦∈ ℝ 𝑛 , 𝑡∈ 𝜏−𝛿,𝜏 , 𝑦 𝜏−𝛿 = 𝑧 0 ,
admits only one solution given by
(3.6) 𝑦 𝑡 =𝒰 𝑡,𝜏−𝛿 𝑧 0 + 𝜏−𝛿 𝑡 𝒰 𝑡,𝑠 ℬ 𝑠 𝑢 𝑠 𝑑𝑠, 𝑡∈ 𝜏−𝛿,𝜏 ,
Definition 3.1. Corresponding with (3.5), we define the following matrix: The Gramian controllability matrix by:
(3.7) 𝒲 𝜏𝛿 = 𝜏−𝛿 𝜏 𝒰 𝜏,𝑠 ℬ 𝑠 ℬ ∗ 𝑠 𝒰 ∗ 𝜏,𝑠 𝑑𝑠.
Proposition 3.1. (See Leiva, Cabada, & Gallo (2020)) The system (3.5) is controllable on 𝜏−𝛿,𝜏 if, and only if, the matrix 𝒲 𝜏𝛿 is invertible. Moreover, a control steering the system (3.5) from initial state 𝑧 0 to a final state 𝑧 1 on the interval 𝜏−𝛿,𝜏 is given by
(3.8) 𝑣 𝛿 𝑡 = 𝐵 ∗ 𝑡 𝒰 ∗ 𝜏,𝑡 𝒲 𝜏𝛿 −1 𝑧 1 −𝒰 𝜏,𝜏−𝛿 𝑧 0 , 𝑡∈ 𝜏−𝛿,𝜏 .
i.e.,
The corresponding solution 𝑦 𝛿 𝑡 of the linear system (3.5) satisfies the boundary condition:
Main Result
This section is devoted to the main result of the present work, i.e., the approximate controllability of the semilinear system in (1.1) with infinite delay, nonlocal conditions and non-instantaneous impulses. According to Abbas et al. (2020), Ayala-Bolagay et al. (2020) for all 𝜙∈𝔎 and 𝑢∈ 𝐿 2 0,𝜏; ℝ 𝑚 , the problem (1.1) admits only one solution 𝑧∈ 𝒫𝒲 ℎ𝜏 , which is given, for 𝑘=1,2,⋯,𝑝, by
(4.9) 𝑧 𝑡 = 𝒰 𝑡,0 [𝜙 0 −𝒦 𝑧 𝜏 1 , 𝑧 𝜏 2 ,…, 𝑧 𝜏 𝑞 0 ] + 0 𝑡 𝒰 𝑡,𝑠 𝑓 𝑠, 𝑧 𝑠 𝑑𝑠 + 0 𝑡 𝒰(𝑡,𝑠) 𝐵 𝑠 𝑢 𝑠 𝑑𝑠, 𝑡∈ 𝐼 0 𝒰 𝑡, 𝑠 𝑘 𝐺 𝑘 𝑠 𝑘 ,𝑧 𝑠 𝑘 − + 𝑠 𝑘 𝑡 𝒰 𝑡,𝑠 𝑓 𝑠, 𝑧 𝑠 𝑑𝑠 + 𝑠 𝑘 𝑡 𝒰 𝑡,𝑠 𝐵 𝑠 𝑢 𝑠 𝑑𝑠, 𝑡∈ 𝐼 𝑘 𝐺 𝑘 (𝑡,𝑧 𝑡 − ) 𝑡∈ 𝐽 𝑘 , 𝜙 𝑡 −𝒦 𝑧 𝜏 1 , 𝑧 𝜏 2 ,…, 𝑧 𝜏 𝑞 𝑡 , 𝑡∈ −∞,0 .
Theorem 4.1. If the functions 𝑓, 𝒢 𝑘 ,𝒦 are smooth enough, condition (1.2) holds, and the linear system (3.5) is exactly controllable on any interval 𝜏−𝛿,𝜏 , 0<𝛿<𝜏, then system (1.1) is approximately controllable on 0,𝜏 .
Proof. Given 𝜙∈𝔎, a final state 𝑧 1 and 𝜖>0, we want to find a control 𝑢 𝜖 ∈ 𝐿 2 0,𝜏; ℝ 𝑚 steering the system to a ball of center 𝑧 1 and radius 𝜖>0 on 0,𝜏 . Indeed, we consider any fixed control 𝑢∈ 𝐿 2 0,𝜏; ℝ 𝑚 and the corresponding solution 𝑧 𝑡 =𝑧 𝑡,0,𝜙,𝑢 of the problem (1.1).
For 
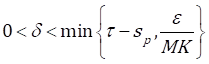 , we define the control 𝑢 𝜖 ∈ 𝐿 2 0,𝜏; ℝ 𝑚 as follows
, we define the control 𝑢 𝜖 ∈ 𝐿 2 0,𝜏; ℝ 𝑚 as follows
where 𝐾= sup 𝑠∈ 0,𝜏 {𝜁(∥𝑧 𝑠 ∥} and
Since 0<𝛿<𝜏− 𝑠 𝑝 , then 𝜏−𝛿> 𝑠 𝑝 ; and using the cocycle property 𝒰 𝑡,𝑙 𝒰 𝑙,𝑠 =𝒰 𝑡,𝑠 , the associated solution 𝑧 𝛿 𝑡 =𝑧 𝑡,0,𝜙, 𝑢 𝜖 of the time-dependent impulsive semilinear retarded differential equation with infinite delay and non-local (1.1), at time 𝜏, can be expressed as follows:
Therefore,
The corresponding solution 𝑦 𝛿 𝑡 =𝑦 𝑡,𝜏−𝛿,𝑧 𝜏−𝛿 , 𝑣 𝛿 of the initial value problem (3.5) at time 𝜏, for the control 𝑣 𝛿 and the initial condition 𝑧 0 =𝑧 𝜏−𝛿 , is given by:
and from Proposition (3.1), we get that
Thus,
(4.10) 𝑧 𝛿 𝜏 − 𝑧 1 ) ≤ 𝜏−𝛿 𝜏 𝒰 𝜏,𝑠 𝑓 𝑠, 𝑧 𝑠 𝛿 , 𝑣 𝛿 𝑠 𝑑𝑠.
Now, since 0<𝛿< 𝑠 𝑝 and 𝜏−𝛿≤𝑠≤𝜏, then 𝑠− 𝑠 𝑝 ≤𝜏− 𝑠 𝑝 <𝜏−𝛿 and
Hence, since 𝛿 satisfies 0<𝛿< min 𝑠 𝑝 ,𝜏− 𝑠 𝑝 , 𝜖 𝑀𝐾 , from (1.3), we get:
which completes the proof.
Final Remark
In this work, we have proved the approximate controllability of a control system governed by a retarded differential equation with unbounded delay, non-local conditions and non-instantaneous impulses, without the need to use fixed point theorems, only applying a technique used by Bashirov & Ghahramanlou (2014), Bashirov & Jneid (2013), and Bashirov et al. (2007). However, to prove exact controllability we can use Rothe's Fixed Point Theorem or a new technique that appears in assuming certain conditions in nonlinear terms on the one hand,or assuming certain conditions on the other hand in the Gramian matrix; this is part of ongoing research. Also, the ideas presented here can be used to study the controllability of infinite-dimensional systems in Hilbert spaces where the dynamical is given by the infinitesimal generator 𝐴 of a compact semigroup {𝑇 𝑡 } 𝑡≥0 , in this case we only get approximate controllability of the system.
Interest conflict
The funders had no role in the study design; in the collection, analysis or interpretation of data; in the writing of the manuscript or in the decision to publish the results.
Authors’ contributions
Following the internationally established taxonomy for assigning credits to authors of scientific articles (https://casrai.org/credit/). The authors declare their contributions in the following matrix: (f1)
















