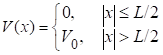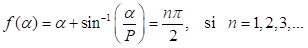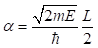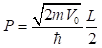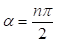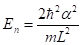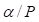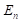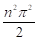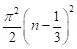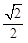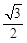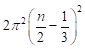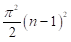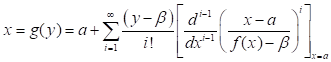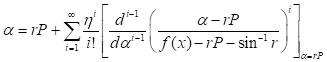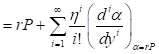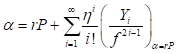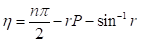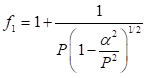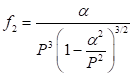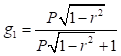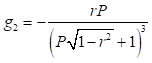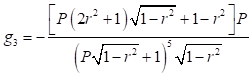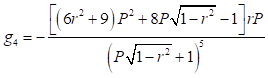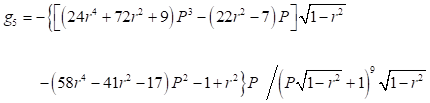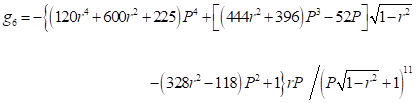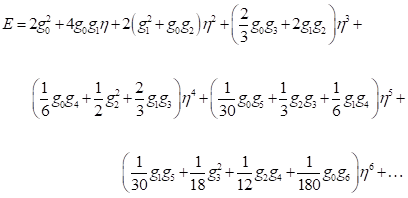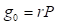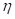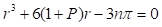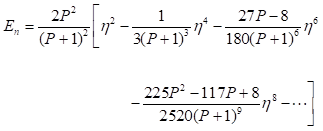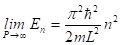Introducción
El problema de una partícula de masa m en un potencial de pozo cuadrado finito es tratado en diversos textos de mecánica cuántica (Cohen, Diu & Laloe, 1977; Landau & Lifshitz, 1977; Messiah, 1961) y constituye, además, un problema básico a resolver en los cursos introductorios de física moderna dada su importancia para modelar partículas ligadas a una cierta región del espacio. Aplicaciones del potencial de pozo cuadrado finito son posibles en física molecular y atómica, física del estado sólido (Mckelvey, 1991) y física nuclear (Park, 1992). En nanotecnología su comprensión forma las bases para el entendimiento de diversas heteroestructuras de baja dimensionalidad, tales como pozos cuánticos en semiconductores (Kolbas & Holonyak, 1984). Desafortunadamente el problema del potencial de pozo cuadrado finito conduce a una solución que contiene ecuaciones trascendentales, lo que impide expresar la solución en una forma matemática concisa. Como consecuencia diversos métodos se han aplicado para resolverlo, incluyendo procedimientos numéricos y gráficos (French & Taylor, 1978; Schiff, 1955; Burge, 1985; Bonfim & Griffiths, 2006). Más allá de los procedimientos tradicionales que puedan encontrarse en los textos de física cuántica, algunas soluciones explícitas y novedosas para este problema han sido publicadas por Sierwert, (1978), Sprung, Wu & Martorell (1992), Aronstein & Stroud (2000), Paul & Nkemzi (2000), Leryonas & Combescot (2002) y Blümel (2005).
En este artículo se discute una solución en serie basada en el teorema de inversión de Lagrange (Jeffrey & Jeffreys, 1972), alrededor de un punto general, y demuestra que un método recursivo introducido en la literatura matemática por (Apostol, 2000), para calcular derivadas de orden superior de una función inversa en términos de la función original, puede usarse para evaluar los términos en la serie.
Metodología
Condición de cuantización y niveles de energía exactos.
Para una partícula en movimiento de masa m, confinada en una caja de longitud L y profundidad V 0, el potencial puede ser escrito como: (0)
Reed (1990) demostró que los niveles de energía para un potencial con estas características pueden obtenerse a partir de una única ecuación trascendental. De esta ecuación y bajo ciertas observaciones Sprung,Wu & Martorell (1992) dedujeron la expresión siguiente (1), en donde las energías de los estados ligados son soluciones de
donde n denota el número cuántico principal. 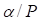 , es una razón de altura e indica una región específica del pozo o región de interés La ecuación (1) establece las condiciones de cuantización para la partícula en el pozo con la interesante novedad de agrupar soluciones pares e impares y de relacionar a n con la escala de acción
, es una razón de altura e indica una región específica del pozo o región de interés La ecuación (1) establece las condiciones de cuantización para la partícula en el pozo con la interesante novedad de agrupar soluciones pares e impares y de relacionar a n con la escala de acción 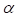 , que depende de la energía E, En general, la importancia de la ecuación (1) sobre sus predecesoras es la aparición explícita del número cuántico. Con ella, por ejemplo (2), se puede determinar directamente el enésimo nivel de energía sin necesidad de encontrar primero las anteriores
, que depende de la energía E, En general, la importancia de la ecuación (1) sobre sus predecesoras es la aparición explícita del número cuántico. Con ella, por ejemplo (2), se puede determinar directamente el enésimo nivel de energía sin necesidad de encontrar primero las anteriores 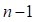 soluciones cuantizadas,
soluciones cuantizadas,
(3)Para un dado valor de P, con
P es una medida de la fuerza de atracción del potencial que depende de la profundidad del pozo. Los niveles de energía para el caso particular del potencial de pozo cuadrado infinito se obtienen de forma inmediata haciendo 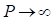 en la ecuación (4), (5) y (6)
en la ecuación (4), (5) y (6)
Otras soluciones exactas y simples como la ecuación (6) son posibles para ‘‘ángulos especiales’’ de 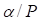 en la ecuación (1). En la tabla 1 se muestran algunos valores de
en la ecuación (1). En la tabla 1 se muestran algunos valores de 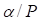 que producen soluciones cerradas para los niveles de energía de la partícula en el pozo finito (Maor, 1988).
que producen soluciones cerradas para los niveles de energía de la partícula en el pozo finito (Maor, 1988).
2.2. Solución general en serie de potencias para los niveles de energía de un potencial de pozo cuadrado finito.
Fórmula de inversión de Lagrange.
Si 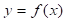 es una función que toma un desarrollo de Taylor en potencias convergentes de x alrededor de algún punto a, con
es una función que toma un desarrollo de Taylor en potencias convergentes de x alrededor de algún punto a, con 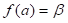 y derivada primera
y derivada primera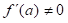 , entonces puede demostrarse que existe una única función
, entonces puede demostrarse que existe una única función 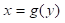 expresable como una serie de potencias en y, la cual converge en algún punto alrededor de a satisfaciendo
expresable como una serie de potencias en y, la cual converge en algún punto alrededor de a satisfaciendo 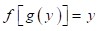 en ese alrededor
en ese alrededor
Fórmulas de Apostol paras derivadas de orden superior.
El teorema de inversión de Lagrange da una expresión formal, ecuación (7), para el desarrollo en serie de potencias de la función 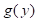 (Jeffreys & Jeffreys, 1972). Dada que ésta es la serie de Taylor para
(Jeffreys & Jeffreys, 1972). Dada que ésta es la serie de Taylor para 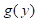 , el término dentro de los corchetes en la ecuación (7) representa la i-ésima derivada de g evaluada en a. A partir de esta observación Apostol (2000) construyó un método para evaluar las derivadas de g, alrededor de un punto arbitrario a, directamente de la función original
, el término dentro de los corchetes en la ecuación (7) representa la i-ésima derivada de g evaluada en a. A partir de esta observación Apostol (2000) construyó un método para evaluar las derivadas de g, alrededor de un punto arbitrario a, directamente de la función original 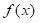 , sin introducir series de potencias y sin la necesidad de diferenciar el cociente
, sin introducir series de potencias y sin la necesidad de diferenciar el cociente 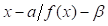 . Apostol (2000) evaluó de forma explícita las derivadas hasta
. Apostol (2000) evaluó de forma explícita las derivadas hasta 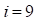 y encontró una fórmula para la
y encontró una fórmula para la 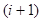 -ésima derivada dada por
-ésima derivada dada por
Donde 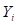 es un polinomio homogéneo en
es un polinomio homogéneo en 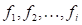 , con coeficientes enteros, que puede determinarse sucesivamente mediante la fórmula recursiva
, con coeficientes enteros, que puede determinarse sucesivamente mediante la fórmula recursiva
Donde 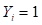 y
y 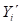 representa la diferenciación de
representa la diferenciación de 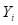 con respecto a x.
con respecto a x.
Fórmulas explícitas para los niveles de energía del pozo finito
De la ecuación (1) hagamos 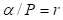 y definamos r como la razón de alturas para el pozo. De esta última relación al despejar
y definamos r como la razón de alturas para el pozo. De esta última relación al despejar 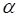 obtenemos un punto alrededor del cual puede evaluarse la serie. En consecuencia, al usar la fórmula de Lagrange, ecuación (7), alrededor de
obtenemos un punto alrededor del cual puede evaluarse la serie. En consecuencia, al usar la fórmula de Lagrange, ecuación (7), alrededor de 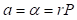 , para invertir la ecuación (10), resulta (11)
, para invertir la ecuación (10), resulta (11)
De la observación de Apóstol (2000) se tiene (12)
Donde (13)
La ecuación (12) puede evaluarse conociendo 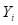 , la cual, a su vez, se obtiene de la relación recursiva ecuación (9) con (14) y (15)
, la cual, a su vez, se obtiene de la relación recursiva ecuación (9) con (14) y (15)
A continuación (16), se dan algunas expresiones explícitas obtenidas para los coeficientes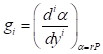 : (17), (18), (19), (20) y (21)
: (17), (18), (19), (20) y (21)
Con esta metodología y con el uso adecuado de algún programa de manipulación simbólica se pueden evaluar tantos términos como uno desee en la serie. De las expresiones dadas para 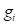 se sigue entonces que la energía E de una partícula en un potencial de pozo cuadrado finito unidimensional como función del número cuántico principal y de la profundidad del pozo está dada por (en unidades de
se sigue entonces que la energía E de una partícula en un potencial de pozo cuadrado finito unidimensional como función del número cuántico principal y de la profundidad del pozo está dada por (en unidades de 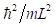 ) (22)
) (22)
Resultados
En lo que sigue se harán algunas consideraciones especiales sobre la ecuación (22) con el objeto de encontrar una aproximación general y dos aproximaciones particulares para el problema de la partícula en una caja unidimensional. Es de hacer notar que estas consideraciones se centraron en la razón de alturas del pozo. Para el caso de las aproximaciones particulares se observó que tomando una razón de alturas adecuada las soluciones obtenidas dan expresiones sencillas para evaluar el espectro de energía de manera muy exacta.
Aproximación general
Una muy buena aproximación puede obtenerse expandiendo hasta el tercer orden en r la expresión dada en la ecuación (13), e igualando a cero, con lo que se resulta, después de algunos rearreglos (23)
Este polinomio tiene sólo una raíz positiva
Dado este caso se observa que la razón de alturas depende de n y P, lo que hace a r un término variable, ideal para evaluar cualquier altura del pozo dado un valor del número cuántico principal.
En la tabla 2, usando la ecuación (24) en la ecuación (22), se comparan las energías calculadas variando P y n con los valores exactos de la ecuación (1). Los cálculos se han extendido hasta potencias de tercer orden en 𝑛 y demuestran que esta aproximación general conduce a soluciones numéricas cuya convergencia ocurre de manera rápida y muy exacta. Incluso usando el primero o segundo término en la serie de potencias en 𝑛 es suficiente para evaluar confiablemente el espectro de energía del pozo finito.
Tabla 2: Aproximación general. Niveles de energía a calculados (en unidades de ℏ 𝑚 𝐿 2 ) usando la ecuación (23) en la ecuación (22). Comparación de resultados con las energías exactas de la ecuación (1).
| P | n | E (exacta) | 1er orden | 2do orden | 3er orden | P | n | E (exacta) | 1er orden | 2do orden | 3er orden | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.00 | 1 | 1.092494 | 1.092433 | 1.092489 | 1.092494 | 6.00 | 1 | 3.616711 | 3.616711 | 3.616711 | 3.616711 | |
| (1.0733) | (1.0971) | (1.0930) | (3.5969) | (3.6167) | (3.6167) | |||||||
| 4.50 | 1 | 3.286656 | 3.286656 | 3.286656 | 3.286656 | 2 | 14.351758 | 14.351755 | 14.351758 | 14.351758 | ||
| (3.2594) | (3.2867) | (3.2867) | (14.2827) | (14.3520) | (14.3518) | |||||||
| 2 | 12.917873 | 12.917841 | 12.917873 | 12.917873 | 3 | 31.773621 | 31.773409 | 31.773621 | 31.773621 | |||
| (12.8347) | (12.9179) | (12.9179) | (31.6624) | (31.7755) | (31.7737) | |||||||
| 3 | 27.882089 | 27.880960 | 27.882014 | 27.882090 | 4 | 54.621390 | 54.620384 | 54.621089 | 54.621401 | |||
| (27.8189) | (27.8912) | (27.8831) | (54.5710) | (54.6323) | (54.6226) |
a Los valores entre paréntesis corresponden a la aproximación de la referencia (Sprung, Wu & Martorell, 1992).
Aproximaciones particulares.
Para este caso introduzcamos como condición que r sea un valor fijo. Dada esta situación podemos examinar dos importantes regiones; el fondo y la mitad del pozo.
Fondo del pozo.
Esta región está descrita por 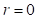 y corresponde a un pozo de profundidad muy grande. Evaluando r en las ecuaciones (16-21) y ecuación (13), y sustituyendo en la ecuación (22), resulta, hasta potencias de octavo orden en
y corresponde a un pozo de profundidad muy grande. Evaluando r en las ecuaciones (16-21) y ecuación (13), y sustituyendo en la ecuación (22), resulta, hasta potencias de octavo orden en 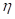 , con
, con 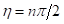 , y en unidades de
, y en unidades de 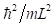 , (25)
, (25)
Para un pozo de profundidad infinita (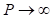 ) esta serie se reduce (26)
) esta serie se reduce (26)
El factor 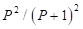 observado en la ecuación (25) distingue los estados ligados más bajos de un pozo finito de aquellos estados correspondiente a un pozo infinito y aparece como un factor de corrección de orden principal en la solución de otros autores (Sprung, Wu & Martorell, 1992; Paul & Nkemzi, 2000).
observado en la ecuación (25) distingue los estados ligados más bajos de un pozo finito de aquellos estados correspondiente a un pozo infinito y aparece como un factor de corrección de orden principal en la solución de otros autores (Sprung, Wu & Martorell, 1992; Paul & Nkemzi, 2000).
Mitad del pozo
Esta región está descrita por 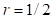 . Haciendo uso de las ecuaciones pertinentes al caso, resulta de la ecuación (22), hasta potencias de cuarto orden en
. Haciendo uso de las ecuaciones pertinentes al caso, resulta de la ecuación (22), hasta potencias de cuarto orden en 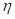 , (en unidades de
, (en unidades de 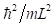 )
)
En la tabla 3 y tabla 4, usando las ecuaciones (25) y (27), respectivamente, se comparan las energías calculadas para distintos valores de P y n con las energías exactas de la ecuación (1). En ambos casos se observa que para valores fuera de la región para la que se ha hecho la aproximación la solución tiende a fallar.
Tabla 3: Fondo del pozo, 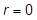 . Niveles de energíab calculados con la ecuación (25). Comparación de resultados con las energías exactas de la ecuación (1).
. Niveles de energíab calculados con la ecuación (25). Comparación de resultados con las energías exactas de la ecuación (1).
| P | Energía exacta | Segundo orden | Cuarto orden | Sexto orden | Octavo orden |
|---|---|---|---|---|---|
| 1.00 | 1.0925 | 1.2337 | 1.1069 | 1.0945 | 1.0928 |
| 2.50 | 2.4665 | 2.5178 | 2.4695 | 2.4667 | 2.4665 |
| 9.0342 | 10.0710 | 9.2983 | 9.1219 | 9.0672 | |
| 4.50 | 3.2867 | 3.3035 | 3.2871 | 3.2867 | 3.2867 |
| 12.9179 | 13.2139 | 12.9526 | 12.9232 | 12.9188 | |
| 27.8821 | 29.7312 | 28.4084 | 28.0744 | 27.9611 | |
| 6.00 | 3.6167 | 3.6256 | 3.6169 | 3.6167 | 3.6167 |
| 14.3518 | 14.5023 | 14.3632 | 14.3529 | 14.3519 | |
| 31.7736 | 32.6301 | 31.9259 | 31.8089 | 31.7829 | |
| 54.6214 | 58.0091 | 55.7835 | 55.1261 | 54.8661 |
b Todos los números están dados en unidades de ℏ 𝑚 𝐿 2 .
Tabla 4: Mitad del pozo, 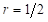 . Niveles de energíac calculados con la ecuación (27). Comparación de resultados con las energías exactas de la ecuación (1).
. Niveles de energíac calculados con la ecuación (27). Comparación de resultados con las energías exactas de la ecuación (1).
| P | Energía exacta | Primer orden | Segundo orden | Tercer orden | Cuarto orden |
|---|---|---|---|---|---|
| 1.00 | 1.0925 | 1.0079 | 1.1139 | 1.0964 | 1.0930 |
| 2.50 | 2.4665 | 2.4314 | 2.4658 | 2.4665 | 2.4665 |
| 9.0342 | 7.8039 | 9.3708 | 9.1552 | 9.0764 | |
| 4.50 | 3.2867 | 1.5103 | 3.2180 | 3.3028 | 3.2833 |
| 12.9179 | 12.7606 | 12.9205 | 12.9181 | 12.9179 | |
| 27.8821 | 24.0110 | 28.4479 | 28.0927 | 27.9612 | |
| 6.00 | 3.6167 | -1.6517 | 3.4235 | 3.6776 | 3.6225 |
| 14.3518 | 14.1558 | 14.3500 | 14.3519 | 14.3518 | |
| 31.7736 | 29.9632 | 31.8440 | 31.7867 | 31.7760 | |
| 54.6214 | 45.7706 | 55.9055 | 55.1886 | 54.8792 |
c Todos los números en unidades de ℏ 𝑚 𝐿 2 .
Discusión
Se ha obtenido una solución general en serie de potencias para el problema de una partícula en un pozo de potencial cuadrado finito unidimesional basada en la fórmula de inversión de Lagrange, alrededor de un punto general, y en las fórmulas de Apostol (2000) para derivadas de orden superior de una función inversa en términos de la función original. A partir de la solución general, ecuación (22), se han examinado algunas aproximaciones al espectro de energía. En la aproximación general los resultados demuestran que la razón de alturas de la ecuación (24) usada en la ecuación (22), en potencias de primero o segundo orden en 𝜂, favorece ampliamente la convergencia de los resultados. Esta razón de alturas se ajusta mejor que la propuesta dada en Sprung, Wu & Martorell (1992). Para los casos particulares de r = 0 (fondo del pozo) y r = 1/2 (mitad del pozo) se han hallado soluciones en serie de potencias hasta sexto y octavo orden en 𝜂, respectivamente. En el caso de r = 0 la serie se simplifica considerablemente. Estas ecuaciones particulares alrededor de un r fijo son útiles para estudiar el espectro de energía en aquellas regiones del pozo para la cuales fueron derivadas las fórmulas.
Por otra parte, considerando valores especiales para 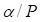 se han encontrado soluciones cerradas a la ecuación de cuantización de la partícula en el pozo finito. Estos resultados pueden ser útiles en procedimientos de interpolación cuyo fin sea el cálculo de las energías de una partícula bajo la influencia de un dado potencial seleccionado aleatoriamente.
se han encontrado soluciones cerradas a la ecuación de cuantización de la partícula en el pozo finito. Estos resultados pueden ser útiles en procedimientos de interpolación cuyo fin sea el cálculo de las energías de una partícula bajo la influencia de un dado potencial seleccionado aleatoriamente.
Conclusiones
La aproximación matemática usada en este trabajo es muy general e incorpora métodos matemáticos elementales, tales como; series de Taylor, funciones inversas y derivadas de orden superior. Su aplicación puede extenderse a otros problemas de la mecánica cuántica de partículas confinadas por barreras finitas en sistemas de dos o incluso de tres dimensiones. Es claro que el problema de una partícula en un pozo de potencial finito tridimensional es mucho más complejo debido a la aparición de un término extra en el hamiltoniano (momento angular), sin embargo, atacar este problema con esta metodología podría ser, como se ha demostrado, una alternativa viable.
Contribución de los autores (rellenar el cuadro con color según la contribución realizada)
En concordancia con la taxonomía establecida internacionalmente para la asignación de créditos a autores de artículos científicos (https://casrai.org/credit/). Los autores declaran sus contribuciones en la siguiente matriz:
Fernández-Rojas, C.
Fernández-Rojas, F.
Conceptualización
Análisis Formal
Investigación
Metodología
Recursos
Validación
Redacción - revisión y edición