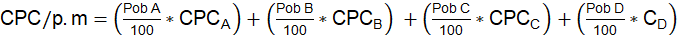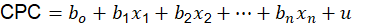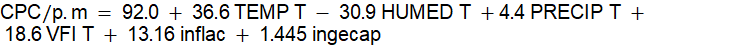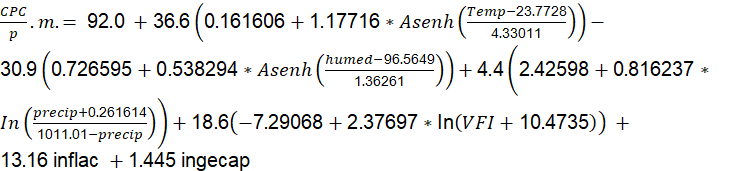1 Introducción
Es evidente la baja cobertura de los sistemas de agua potable en muchas ciudades del mundo, el impacto del cambio climático en los caudales de las fuentes de agua cruda y la desactualización de políticas de conservación efectivas del recurso (UNESCO, 2009). En investigaciones previas (Bayas, 2018; Bravo & Merino, 2018; Eras, 2019; Flores, 2019; Lindao, 2018) se analizaron las relaciones de algunas variables con el consumo de agua potable residencial en 11 ciudades ecuatorianas, menores a 150 000 habitantes.
El territorio continental ecuatoriano está atravesado por la cordillera de los Andes de Norte a Sur, que lo divide en tres regiones naturales: Litoral (Costa), Región Interandina (Sierra) y Región Oriental (Amazonía). Las ciudades muestreadas corresponden a las regiones litoral (1), interandina (8) y oriental (2), ver tabla 1. Cada región tiene una diversidad de climas debido a su cercanía a la línea ecuatorial en donde convergen los vientos alisios provenientes de ambos hemisferios. Su desplazamiento genera perturbaciones tropicales, nubosidad densa y precipitaciones de intensidad variable. Este desplazamiento marca dos estaciones al año en el Ecuador Continental: una lluviosa y otra seca (Guillén, 2014). En esos estudios el consumo per cápita (CPC) de agua potable (variable dependiente) fue medido mensualmente durante 6 meses en cada ciudad.
Los grupos de variables estudiados (variables independientes) son: climatológicos; sociodemográficos; socioeconómicos; y, de gestión y calidad del agua. Esas variables son: 1) casas que reportan fugas; 2) número de aparatos sanitarios: inodoros, lavamanos, lavadoras de ropa, lavavajillas, duchas; 3) casas con jardines; 4) adquisición agua embotellada en bidones; 5) tipo de almacenamiento de agua: cisterna, tanque elevado, tanque de lavar ropa; 6) número de veces que cocinan en casa; 7) número de personas por familia; 8) tamaño de la población; 9) costo del agua; 10) percepciones organolépticas de la calidad de agua: olor, color sabor, presencia de tierra; 11) índice de gestión y calidad del agua (Ingecap); 12) inflación acumulada; 13) precipitación; 14) humedad atmosférica máxima; y, 15) temperatura. Algunas de estas variables fueron obtenidas mensualmente (11; 12; 13; 14 y 15) y las otras semestralmente.
Las características socioeconómicas, demográficas, climatológicas, de gestión y de calidad del agua potable de cada ciudad investigadas entre el 2013 y el 2015, fueron reportadas por Barreno (2015), Cáceres & Rubio (2015), Carrillo & Quintero (2013), Montenegro & Tapia (2014), Morillo & Luna (2013), Noriega (2015), Patiño & Pino (2014), Sagñay & Carguachi (2015) y Samaniego & Muela (2015). El procesamiento de esa información primaria, integrando los resultados de todas las ciudades, se lo reporta desde el 2018. Estos últimos reportes analizan 2 variables independientes en cada reporte, contra la variable dependiente CPC. En algunos casos también se investigaba si había correlaciones entre las variables independientes.
Se ha encontrado que casi todas las variables tienen relaciones positivas o negativas con el CPC de agua potable. Arellano, Bayas, Meneses y Castillo (2018) reportaron similitudes de consumos en tres rangos poblacionales (ciudades grandes, medianas y pequeñas) y la influencia significativa de la humedad atmosférica máxima y de la temperatura máxima. Además, evidencian las tendencias diferentes de los consumos de agua entre los 4 estratos socioeconómicos: A, B, C y D, previamente investigados El estrato A es de mayores recursos económicos y el D es de menores recursos.
Arellano & Lindao (2019) evidencian que las percepciones organolépticas del usuario afectan negativamente en el consumo de agua potable de la red pública. Debido a la desconfianza en la calidad del agua pública, adquieren agua embotellada en bidones, lo cual está relacionado con el estrato socioeconómico al que pertenecen. Fan, Liu, Wang, Geissen & Ritsema (2013) analizan variables similares a los de este estudio, pero lo focalizan al sector rural de la cuenca del Río Wei en China. A pesar de las diferencias geográficas, climáticas y sociodemográficas, el análisis arroja resultados comparables con esta investigación. Algunas de las variables de este estudio también coinciden con los de Jiménez, Orrego, Vásquez & Ponce (2017) aunque su enfoque econométrico lo dirige hacia la definición de tarifas en Manizales, Colombia. Las tarifas no están alejadas del alcance de esta investigación ya que proporcionaría importante información para ese objetivo también (Gascon, Arregui, Cobacho, & Cabrera, 2004; Santopietro et al., 2018).
Cada una de las variables afectaría el consumo de agua potable, con diferencias en los rangos poblacionales y en los estratos socioeconómicos. Por lo tanto, la incidencia cuantitativa de cada variable podría ser diferente. Una de las aristas más relevantes de este estudio es la consideración de variables socioeconómicos que han sido poco estudiados por otros investigadores. En general la falta de información actualizada para predecir el consumo de agua potable de una población, podría ser la causa de los sistemas de agua potable deficitarios existentes en muchos países en desarrollo.
Esta investigación integra las variables estudiadas desde el 2013 en Ecuador para definir los modelos matemáticos que predicen el consumo de agua potable residencial. Esta información será útil para proyectistas, planificadores y responsables de la gestión del recurso, con la finalidad de optimizar las dotaciones de los sistemas de agua potable y garantizar una distribución equitativa en las redes de distribución.
Metodología
Cada una de las ciudades investigadas fue caracterizada de acuerdo al Método de caracterización urbanística y socioeconómica (Arellano, González & Gavilanes, 2012) de donde se han obtenido los estratos existentes en cada ciudad, ver tabla 1. Se investigaron 746 residencias durante 6 meses en las 11 ciudades. Los registros
de los consumos mensuales leídos de los medidores de agua son 4 476.
Este estudio analiza las correlaciones entre todas las variables y el CPC de agua potable. El análisis considera dos escenarios separados:
A) consumos de agua potable de cada estrato socioeconómico (CPC/est.s), su valor mensual promedio de 6 meses de registros; y B) consumos mensuales de agua potable de cada ciudad (CPC/p.m). Esta última variable fue reportada por los autores (2013-2015), como los valores representativos de la ciudad y fueron ponderados considerando las fracciones de cada estrato socioeconómico existentes, ver ecuación (1).
Tabla 1 : Características demográficas, geográficas y socioeconómicas de las ciudades muestreadas.
| Rango Poblacional | Región | Ciudad | Altura m.s.n.m. | Habitantes 2010 | Número de residencias muestreadas | Estratos socio económicos |
| Ciudades pequeñas 500-8000 | Interandina | Columbe | 3100 | 526 | 43 | B,C,D |
| Cubijíes | 2501 | 588 | 45 | B,C,D | ||
| Guamote | 2560-3000 | 2648 | 53 | B,C,D | ||
| Chambo | 2400 | 4459 | 46 | B,C,D | ||
| Químiag | 2879 | 5357 | 45 | B,C,D | ||
| Guano | 2794 | 7758 | 59 | B,C,D | ||
| Ciudades medianas 8000-30000 | Amazónica | Joya de los Sachas | 270 | 11480 | 52 | B,C,D |
| Macas | 1050 | 18984 | 74 | A, B,C,D | ||
| Interandina | Guaranda | 2668 | 23874 | 49 | A,B,C | |
| Ciudades grandes 30000-150000 | Costera | Ventanas | 25 | 38168 | 97 | A, B,C,D |
| Interandina | Riobamba | 2764 | 146324 | 183 | A, B,C,D |
Elaborado por Bayas (2018; Bravo & Merino (2018), modificado por los Autores
En donde:
CPC/p.m: consumo per cápita ponderado mensual, de agua potable, considerando la estratigrafía socioeconómica de la ciudad;
CPCi: consumo per cápita de agua potable del estrato i (i puede ser A, B, C y D). Se obtiene calculando el promedio aritmético de los registros mensuales del estrato i;
Pob i: fracción de manzanas correspondientes al estrato i (i puede ser A, B, C y D), con relación al total de las manzanas residenciales de la ciudad.
Para verificar si los modelos cumplen con los supuestos de normalidad y homocedasticidad de los residuos, se realizó la validación a través de la prueba de normalidad y de la prueba de homocedasticidad. Si el valor p es mayor al 5% se aceptó la hipótesis de que los datos proceden de una población normal. Si el valor de p es menor al 5% significa que los datos no proceden de una población normal y se aplicó la transformación de datos de Johnson para normalizarlos. El análisis estadístico se realizó por medio de regresiones lineales múltiples. La regresión múltiple sirve para entender situaciones complejas, donde influyen más de dos variables (Montero, 2016). Con este modelo se evalúa los efectos de las variables, ver tabla 2 y tabla 3, que influyen en el consumo del agua potable mediante una ecuación lineal, en cada escenario separadamente.
En donde:
CPC: es el consumo per cápita de agua potable CPC (lt/hab-día);
X1-n: son las variables;
u: son los residuos;
b1-n: son los coeficientes de cada variable.
Los coeficientes son valores que indicarían la incidencia directa de cada variable en el consumo de agua potable del sector residencial, semestral o mensualmente. Si se los ordena de acuerdo con su significancia estadística, se dimensionaría su incidencia y se comprendería su importancia en el consumo del agua potable. En la construcción de los 2 modelos matemáticos se consideran todas las variables.
Se utilizó el Software Minitab versión 2017 (State College, PA. EUA). En el análisis de varianza se presenta: 1) los grados de libertad GL (número de variables); 2) suma ajustada de cuadrados SC Adjust; 3) cuadrados medios ajustados MC Adjust; 4) valor F; y, 5) valor p. El valor p indica la significancia de las variables con respecto a la variable respuesta. Si el valor p es menor que 0.05, indica un nivel de confianza del modelo del 95% (MINITAB, 2017). Para determinar el ajuste del modelo a los datos, se observa la desviación estándar S, el porcentaje de variación en la respuesta R2, el porcentaje de variación en la respuesta ajustado para el número de predictores R2 ajustado y el porcentaje de variación pronosticado R2. El R2 ajustado varía de 0% a 100%. Mientras más se acerca al 100% más se ajusta a los datos (MINITAB, 2017).
3 Resultados y discusión
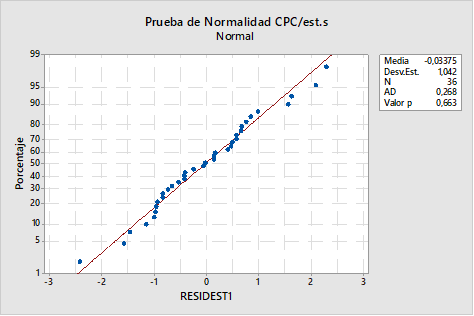
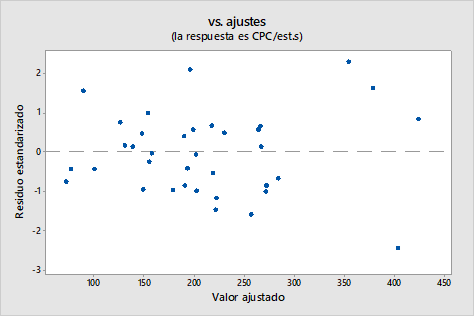
Los datos de los consumos per cápita semestral de agua potable (escenario A) cumplen con la prueba de normalidad (figura 1: valor p=0.663) y sus valores están distribuidos de forma aleatoria y balanceada, ver figura 2.
Los valores p obtenidos del ANOVA se han ordenado ascendentemente como se observa en las tabla 2 y tabla 4. En las filas superiores se encuentran los variables que tienen más significancia estadística (valor p<0.05). En el escenario A, ver tabla 2, solo se obtienen 2 variables (de un total de 19) con significancia estadística: consumo de bidones per cápita (valor p=0.005) y número de personas por familia en cada estrato a (valor p=0.041).
Tabla 2 : Análisis de regresión del consumo per cápita semestral de agua potable (CPC/est.s.).
| variables | abreviatura | GL | valor p | coeficientes |
| - | Regresión | 19 | 0.000 | |
| - | Constante | 0.860 | 94.000 | |
| Consumo bidones Per Cápita. | bidon_per | 1 | 0.005 | 254.800 |
| Número de personas por familia en cada estrato. | Hab_vi | 1 | 0.041 | -26.900 |
| Tanque de ropa | tanq_rop | 1 | 0.055 | 1.157 |
| Tiene Sabor | sabor | 1 | 0.109 | 3.090 |
| Tanque Elevado | tanq_elev | 1 | 0.165 | - 0.976 |
| Índice de gestión y calidad de agua potable. | ingecap | 1 | 0.187 | 6.580 |
| Humedad Atmosférica máxima | humed | 1 | 0.203 | -2.440 |
| Número de Aparatos Sanitarios per cápita | Equi_san | 1 | 0.204 | -23.600 |
| Inflación Acumulada | inflac | 1 | 0.271 | -47.700 |
| Tiene Tierra | tierra | 1 | 0.278 | 0.819 |
| Tiene Color | color | 1 | 0.297 | 0.773 |
| Cisterna | cisterna | 1 | 0.312 | 0.973 |
| Número de veces que cocinan en casa. | Cocin_3 | 1 | 0.424 | -0.525 |
| Porcentaje de casas con jardines en cada estrato. | vi_jar | 1 | 0.490 | -0.438 |
| Precipitación. | precip | 1 | 0.504 | 1.010 |
| Viviendas que reportan fugas intradomiciliarias. | VFI | 1 | 0.540 | 0.910 |
| Pago per cápita. | pago_per | 1 | 0.601 | -11.300 |
| Tiene Olor | olor | 1 | 0.702 | -0.910 |
| Temperatura máxima | Temp | 1 | 0.904 | -3.500 |
| - | Error | 16 | - | - |
| - | Total | 35 | - | - |
en donde:
Temp Temperatura máxima (°C);
humed Humedad Atmosférica máxima (%);
inflac Inflación Acumulada (%);
Precip Precipitación (mm);
ingecap Índice de gestión de calidad de agua potable (%);
bidon_per Consumo bidones Per Cápita (lt /hab/día);
olor Tiene Olor (%);
color Tiene Color (%);
sabor Tiene Sabor (%);
tierra Tiene Tierra (%);
tanq_elev Tanque Elevado (%);
cisterna Cisterna (%);
tanq_rop Tanque de ropa (%);
Equi_san Número de Aparatos Sanitarios per cápita (unidad/persona);
pago_per Pago per cápita ($/m3);
vi_jar Porcentaje de casas con jardines en cada estrato (%);
VFI Viviendas que reportan fugas intradomiciliarias (%);
Hab_vi Número de personas por familia en cada estrato (hab/vivienda);
cocin_3 Número de veces que cocinan en casa (%).
Tabla 3 : Análisis de varianza del consumo per cápita semestral de agua potable (CPC/est.s.).
| Desviación estándar S | R2 | R2 (ajustado) | R2 (predictivo) |
| 39.3619 | 91.25% | 80.87% | 43.97% |
La ecuación (3), obtenida con el modelo estadístico de regresión múltiple, tiene un R2 ajustado de 80.87% dejando una incertidumbre de 19.13%, ver tabla 3. Podría usarse con fines predictivos para calcular el CPC/est.s de una ciudad. Todos los coeficientes obtenidos en el análisis de regresión (tabla 2) conforman la ecuación (3) de esta manera (Montero, 2016).
Las variables que inciden en el CPC/est.s, ver tabla 2, son más numerosos que los que inciden en el CPC/p.m., ver tabla 4, debido a las siguientes razones. Algunos datos primarios fueron obtenidos una sola vez en el semestre y no mensualmente; por ejemplo, el número de aparatos sanitarios, el tipo de tanque en donde almacenan el agua y las percepciones organolépticas. Adicionalmente, los datos para el análisis semestral son muchos más en cantidad que los del análisis mensual debido a que el primero considera individualmente a los valores de cada estrato socioeconómico (A, B, C y D); en cambio el segundo los integra y obtiene un solo valor, ecuación (1).
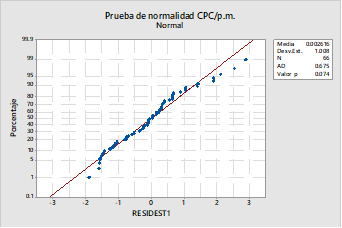
El modelo para calcular el CPC mensual de agua potable (escenario B) no cumple con el supuesto de normalidad y la distribución de sus datos no está balanceada. Por esta razón se realizó la transformación de datos de Johnson a las variables: humedad atmosférica máxima, temperatura máxima, viviendas que reportan fugas intradomiciliarias y precipitación. Esta transformación generó fórmulas trigonométricas y logarítmicas que remplazaron a los datos originales para que sigan una distribución normal (MINITAB, 2017).
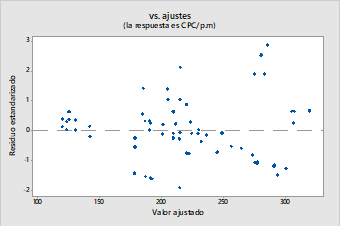
Para validar este nuevo modelo se aplicó la prueba de normalidad, ver figura 3, donde se destaca que el valor p=0.074 es mayor que 0.05; por lo tanto, se puede afirmar que los datos proceden de una distribución normal. En la figura 4 se verifica que los datos se distribuyen aleatoriamente.
Tabla 4: Análisis de regresión de consumo per cápita ponderado mensual (CPC/p.m.) con variables transformadas.
| variables | fuente | GL | valor p | coeficiente |
| Regresión | 6 | 0.000 | - | |
| Constante | 0.171 | 92.0 | ||
| Humedad atmosférica máxima Transformada | HUMED T | 1 | 0.004 | -30.9 |
| Temperatura máxima transformada. | TEMP T | 1 | 0.007 | 36.6 |
| Viviendas que reportan fugas intradomiciliarias. | VFI T | 1 | 0.089 | 18.6 |
| Inflación Acumulada. | inflac | 1 | 0.100 | 13.16 |
| Precipitación transformada. | PRECIP T | 1 | 0.740 | 4.4 |
| Índice de gestión de calidad de agua potable. | ingecap | 1 | 0.104 | 1.445 |
| - | Error | 47 | - | - |
| - | Total | 53 | - | - |
Los datos de temperatura, humedad y precipitación tienen valores diferentes porque provienen de las 3 regiones geográficas ecuatorianas que tienen distintas y bien marcadas características climatológicas.
Con las variables transformadas, ver tabla 4, se generó otra matriz a la que se le aplicó el análisis de varianza. Arrojó los siguientes valores de p (tabla 4) ordenados ascendentemente. La variable humedad atmosférica máxima transformada (p=0.04) y la temperatura máxima transformada (p=0.007) son estadísticamente significativos (p<0.05). Para construir este modelo se utilizaron todos los coeficientes a pesar de que algunos tenían un valor p alto (mayor que 0.05) y se obtuvo una correlación R2 = 38.88%. El modelo B (CPC/p.m) serviría para estimar el consumo de agua potable mensual en las ciudades ecuatorianas, con una incertidumbre de 61.12%, ver ecuación (4). Si se eliminaban los coeficientes cuyo valor p era mayor que 0.05, la incertidumbre aumentaba.
Al reemplazar las fórmulas de la transformación en las variables correspondientes, se obtiene la ecuación de regresión (5).
en donde:
Temp Temperatura máxima (°C);
humed Humedad Atmosférica máxima (%);
inflac Inflación Acumulada (%);
precip Precipitación (mm);
ingecap Índice de gestión de calidad de agua potable (%);
VFI Viviendas que reportan fugas intradomiciliarias (%).
El coeficiente de la constante del escenario A es 94 (tabla 2), es parecido al del escenario B, que es 92 (tabla 4). Estos indican el CPC mínimo semestral o mensual de las líneas de regresión cuando los valores de las variables son iguales a cero. Es el CPC mínimo de agua potable.
La transformación de variables introdujo fórmulas matemáticas en función de las variables originales. La humedad atmosférica máxima y temperatura máxima son algunas de las variables que caracterizan el clima (García, 2012) y son los de mayor significancia estadística en el escenario B. Por lo tanto, se puede afirmar que esas variables climatológicas inciden significativamente en el consumo mensual de agua potable (CPC/p.m). Considerando el signo de los coeficientes de los 2 modelos, la humedad es negativa en los 2, lo que significa que cuando aumenta el valor de la humedad disminuye el consumo mensual de agua potable.
El signo de la temperatura máxima es negativo en el modelo A y positivo en el modelo B. Si la temperatura máxima aumenta, el CPC/p.m. también aumenta, pero el CPC/est.s disminuye. En Manizales (Colombia) que se encuentra en la región interandina, también se reporta un coeficiente negativo (Jiménez et al., 2017). El efecto de la precipitación en la misma ciudad de Manizales se reporta con signo negativo mientras que en este estudio es positivo en los 2 modelos. La variedad de datos climatológicos de las 3 regiones ecuatorianas podría ser la razón para que exista esa diferencia de signos entre los modelos de consumos semestral y mensual.
El coeficiente de la variable viviendas que reportan fugas intradomiciliarias es positivo. Significa que si su valor sube el consumo de agua potable se incrementa. Si se atribuyese que las fugas intradomiciliarias de una residencia estarían relacionadas al deterioro del inmueble, se podría comparar con los resultados de Jaramillo-Mosqueira (2005), que reportó que los consumos de agua potable aumentan cuando las residencias tienen más años de vida y por lo tanto aumentaría su deterioro e ineficiencia, en México. También podría atribuirse a que los usuarios no se interesan en reparar los daños de sus instalaciones hidro-sanitarias probablemente debido a que el precio del agua potable es barato y por lo tanto sus consumos altos debido a las fugas no les afecta económicamente.
La inflación acumulada no tiene relevancia estadística en ningún escenario, pero su tendencia es opuesta en los dos modelos, positiva en el consumo mensual y negativa en el consumo semestral. La inflación acumulada semestral sube y el consumo de agua potable baja. Podría atribuirse a que los usuarios no regresen a casa durante el día debido a limitaciones económicas y por lo tanto su consumo de agua residencial disminuya (Bravo & Merino, 2018), especialmente en las ciudades donde los estratos socioeconómicos limitados de recursos sean predominantes. Esto se refleja en el modelo A para calcular los consumos semestrales porque en este se consideran las características socioeconómicas de cada estrato individualmente. Por eso no se refleja en el modelo B de consumos mensuales de agua potable.
El costo del agua potable está representado por el pago per cápita, por cada m3 de agua consumida. Esta variable también tiene coeficiente negativo. Se incrementa el costo del m3 de agua y disminuye su consumo, lo que corrobora algunos reportes (Bravo & Merino, 2018; Fan et al., 2013; Frausto, 2015; Reynaud & Romano, 2018; Romano, Salvati & Guerrini, 2014; Sahin, Bertone & Beal, 2017).
De acuerdo a Arellano & Lindao (2019) el consumo de agua embotellada (consumo bidones per cápita) se debe a la desconfianza del usuario en la calidad del agua de la red pública y a su capacidad económica, observando diferencias entre ciudades grandes, medianas y pequeñas. Los mismos autores afirman que existen correlaciones lineales muy fuertes y perfectas entre el índice de gestión y calidad del agua potable (Ingecap) y las percepciones organolépticas olor, color y sabor del agua de la red pública. El Ingecap evalúa la gestión y la calidad del agua a través de 6 parámetros: (1) color, 2) turbiedad, 3) pH, 4) cloro residual, 5) coliformes totales y 6) sólidos totales disueltos (STD). Por lo tanto, la calidad del agua aparece directa e indirectamente como una variable que incide significativamente en el modelo A de consumo de agua semestral, con signo positivo. Mejora la calidad del agua y/o las percepciones organolépticas y/o el Ingecap; y, aumenta el consumo de agua semestral. Nauges & Bontemps (2009) reportaron que la calidad del agua de la red pública influye en la decisión de beber agua embotellada, en Francia.
Las conclusiones de Doria (2006) coinciden con las razones descritas antes aunque su amplia revisión bibliográfica se refiere especialmente a países desarrollados (Estados Unidos, Canadá y Francia). Esto coincide con el reporte de Zetland (2016) que afirma que el consumo de agua en Inglaterra y Gales (Reino Unido) disminuye cuando el sabor del agua cambia independientemente del precio del agua. Según Reynaud & Romano (2018) en algunos países desarrollados, especialmente en Estados Unidos y España, también disminuye drásticamente el consumo de agua potable cuando su calidad se deteriora. La calidad del agua, evaluada por los usuarios a través de sus percepciones organolépticas, sería una de las principales causas para que los usuarios beban agua embotellada, según los autores mencionados arriba.
La variable demográfica tiene significancia estadística (valor p=0.041) en el consumo semestral de agua en las ciudades ecuatorianas, pero su coeficiente es negativo. Aumenta el número de habitantes por familia y disminuye el consumo semestral de agua potable. El consumo de agua potable aumenta cuando se incrementa el número de habitantes por familia (Jaramillo-Mosqueira, 2005; Jiménez et al., 2017) fue reportado en México y Manizales (Colombia) mientras que en Ecuador y Londres (Reino Unido) disminuye (Morote, 2017) . Estas aparentes contradicciones del efecto del número de personas por familia en el consumo de agua potable del sector residencial deberían ser analizadas en un contexto socioeconómico y no solo demográfico.
La identificación y la categorización de estas variables así como la definición de estos modelos matemáticos, proporcionan herramientas muy útiles para definir políticas para la conservación y optimización del uso del agua potable (Reynaud & Romano, 2018) y para distribuirla de una forma más equitativa de manera que su impacto social disminuya (Zetland, 2016).
4 Conclusión
Solamente dos (de las 19) variables “calidad del agua potable” y “demografía” inciden significativamente en el consumo semestral de agua potable. Las variables climatológicas (humedad atmosférica máxima y temperatura máxima) tienen más significancia estadística que las otras 4 variables que intervienen en el consumo mensual de agua potable.
Se obtienen dos modelos matemáticos que pueden ser utilizados para calcular los consumos per cápita de agua. El modelo A calcula el consumo per cápita cuando se ha obtenido datos mensuales durante un semestre y corresponden a cada estrato socioeconómico presente en una ciudad (CPC/est.s). El modelo B estima el consumo per cápita mensual sin considerar individualmente a los estratos socioeconómicos (CPC/p.m). El modelo A requiere como datos los valores de 19 variables mientras que el modelo B requiere solamente seis variables. La incertidumbre relativamente alta del modelo B sugiere buscar otro modelo matemático para disminuirla. Sin embargo, este modelo no deja de ser una herramienta importante para estimar el caudal de agua necesario en una ciudad debido a los pocos datos requeridos, por lo cual sería más accesible para los usuarios.
Los consumos mínimos de agua potable en las ciudades menores que 150 000 habitantes se encuentran entre 94 y 92 lt/hab-día, cuando todas las variables analizadas tengan valores iguales a cero.
Los dos modelos son importantes herramientas para los planificadores y proyectistas, para determinar las dotaciones de agua de los sistemas de abastecimiento de agua potable y optimizar el uso del recurso. Sin embargo, por la naturaleza dinámica de las variables, la actualización de sus datos garantizará el manejo sostenible del recurso.