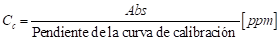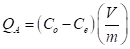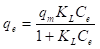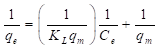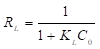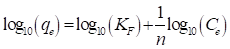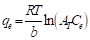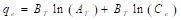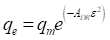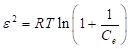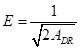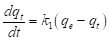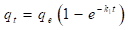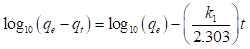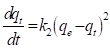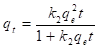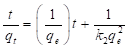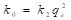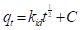Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
La industria textil desempeña un papel importante en el desarrollo económico del Ecuador. Sin embargo, crea serios problemas para el medio ambiente, en particular en la eliminación de las aguas residuales con alto contenido de colorantes (Rahman, Urabe, & Kishimoto, 2013).
Actualmente, se producen alrededor de 700.000 toneladas de compuestos orgánicos y más de 100.000 diferentes tipos están disponibles en el mercado; de estos los colorantes azoicos representan la clase más grande de tintes textiles (Kroumov, 2014). En el proceso de dar color a los textiles se pierde del 10% al 25% de estos colorantes y del 2% al 20% son descargados directamente a efluentes (Baban, Yediler, & Ciliz, 2010). En el tratamiento de las aguas residuales de textilerías y en particular para remover colorantes se han empleado procesos biológicos, químicos y físicos. Dentro de estos tratamientos se encuentran los basados en floculación, coagulación, agentes oxidantes, procesos de membrana, procesos electroquímicos, entre otros.
En general, estos procesos tienen elevados costos y la industria rara vez los aplica (Budnyak, Vlasova, Golovkova, Slabon, & Tertykh, 2019). Sin embargo, una alternativa de bajo costo es el uso de arcillas. Las arcillas tienen una gran capacidad de adsorción debido a su estructura, ya que poseen una alta área superficial y una superficie con sitios activos para la adsorción (Zhao et al., 2013). La adsorción y desorción de moléculas orgánicas están controladas por las propiedades de la superficie de la arcilla y las propiedades químicas de las moléculas que se adsorben (Pleşa, Tănase, Bedelean, & Măicăneanu, 2016). Además, las partículas de arcillas exhiben propiedades fisicoquímicas interesantes para este tipo de aplicación, tales como, alta capacidad de intercambio catiónico, un gran potencial catalizador y adsorbente (Elmoubarki et al., 2015).
El Ecuador cuenta con una gran cantidad de textilerías, de las cuales se estima que un 80% no realizan ningún tratamiento a sus aguas residuales y con frecuencia estas aguas son vertidas a fuentes hídricas principales (Figueroa, 2012). Sin embargo, en el país existe un gran número de depósitos naturales de arcillas, y existe muy pocos estudios sobre el potencial que tienen estas arcillas como material adsorbente de bajo costo para el tratamiento de efluentes con colorantes.
El objetivo de esta investigación fue estudiar la adsorción de un colorante catiónico Drimaren Yellow CL-2R y un colorante aniónico Basic Navy Blue 2 RN en tres tipos de arcillas de los depósitos naturales de Cochancay, Santa Clara y Shirahuan. Para alcanzar este objetivo se evaluó el mecanismo de adsorción ajustando tres modelos de adsorción a los datos experimentales.
Metodología
Colorantes
El colorante catiónico Basic Azul Marino 2RN (CC) es una mezcla de colorantes básicos que se usa para teñir en la industria textil, cuero y papel. No se debe verter en desagües ni cursos de agua, es muy tóxico para los organismos acuáticos y puede provocar a largo plazo efectos negativos en el medio ambiente. Su principal componente (35 % a 45 %) es el oxalato verde de malaquita con número de identificación CAE:2437-29-8, fórmula C52H54N4O12 y su estructura se muestra en la figura 1.
Figura 1: Estructura del principal componente del colorante Basic Azul Marino 2RN. (Ali, Alhassani, Karuvantevida, Rauf, & Ashraf, 2014).
Colorante Aniónico Drimaren Amarillo CL-2R (CA), este tipo de colorante es utilizado generalmente para la tintura y estampación de tejidos de algodón y poliéster, el colorante Drimaren Amarillo CL-2R es de tipo monoazoico y es además un colorante reactivo de monocloro-triazina el cual requiere una temperatura mayor a 80°C y un pH elevado (pH 11) para fijarse a las fibras, cuya estructura se puede apreciar en la figura 2.
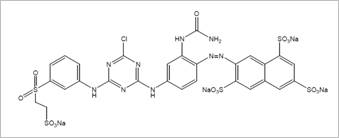
Figura 2: Estructura del colorante Drimaren Amarillo CL-2R Fuente: (Ali, Alhassani, Karuvantevida, Rauf, & Ashraf, 2014).
Caracterización y preparación de las arcillas
Las muestras de arcilla fueron recolectadas de los depósitos naturales -minas- de Cochancay, ubicada en la provincia del Azuay con las coordenadas UTM (x=689719; y=9727775), Santa Clara situada en la ciudad del Puyo provincia de Pastaza (x=846165; y=9858680) y Shirahuan perteneciente al cantón Echeandía provincia de Bolívar (x=697343, y=9858680). En lo que sigue a las arcillas provenientes de la mina de Cochancay, Santa Clara y Shirahuan se les etiqueta con las letras CO, SC y SH, respectivamente.
Las arcillas fueron trituradas con un molino, pulverizadas en un mortero mediante un pistilo, y pasadas por un tamiz 0.05 µm. Luego, las arcillas fueron activadas en un medio ácido usando HCl con una concentración de 2N por cada 200 g de arcilla.
El análisis químico elemental de las muestras (expresado en porcentaje en peso de óxidos) se ejecutó usando un espectrómetro de fluorescencia de rayos-x (S1 TURBOSD handles XRF analyzer, Bruker, UK). Las fases minerales en cada arcilla fueron analizadas con el difractómetro de rayos-x (D8 Advance, Bruker, UK) equipado con un ánodo de cobre (λ=1.5418 Å) y un detector lineal (LynxEye compound silicon strip detector, Bruker, UK). Los difractogramas fueron colectados en un rango de 4 a 100 grados, con un paso de 0.02 grados y un tiempo de medida de 2 segundos por paso. El análisis semicuantitativo del difractograma se realizó a través de su comparación con espectrogramas estándar usando el software DIFFRAC.SUITE EVA, Bruker, UK.
Determinación del porcentaje de remoción y la concentración del colorante en solución
Para evaluar la efectividad de las arcillas en la remoción de colorantes, se realizan medidas de absorbancia óptica en un Espectrofotómetro de UV-visible. Para obtener el factor multiplicador que permite llevar las medidas de absorbancia a concentración, se debe preparar una curva de calibración, empleando soluciones con diferentes concentraciones conocidas de colorantes (Budnyay et al., 2019).
Para la obtención del nivel de absorbancia se empleó el espectrofotómetro de UV-Vis HACH 5000, a partir de estos niveles se determinó la concentración (C c ) de colorante en las muestras de aguas sintéticas preparadas empleando la siguiente fórmula:
En la ecuación (1), Abs, representa el valor de absorbancia medido. La pendiente de la curva de calibración se obtuvo ajustando una línea recta a los valores de absorbancia que se midieron en 10 muestras de agua sintética con diferentes concentraciones de colorante. Para la determinación del porcentaje de remoción y la concentración del colorante en la solución se usaron las expresiones en las ecuaciones (2) y (3). Las medidas de absorción se realizaron a una longitud de onda de 650 nm para el CC y 422 nm para el CA.
El porcentaje de colorante removido (R) de la solución después de haber transcurrido un tiempo de contacto t c con el absorbente, se determina usando la ecuación (2). Mientras que, la cantidad de colorante adsorbido por el adsorbente - capacidad de adsorción (Q A ) - después de haber transcurrido un tiempo de contacto t c , expresada en mg de colorante removido por gramo de adsorbente sólido, se determina usando la ecuación (3).
En la ecuación (2) y (3), C o representa la concentración inicial del colorante en la solución y es expresada en ppm (mg/L); C e (mg/L) simboliza la concentración de equilibrio del colorante en la solución después de haber transcurrido un tiempo de contacto t c con el absorbente (la arcilla); V representa el volumen de la solución y es expresado en litros y m es la etiqueta para la masa de absorbente sólido expresada en gramos.
2.4 Efecto del pH en la remoción del colorante
Para estudiar el efecto del pH se prepararon soluciones coloreadas con un pH de 2, 4, 6, 8, 10 y 12. Se usó un volumen de 50 mL, con una concentración del colorante de 80 (mg/L) y la cantidad de arcilla fue de 0.30 g. Se midió la absorbancia en cada una de las soluciones una vez transcurrido un tiempo de contacto igual a 15 min. Este procedimiento se repitió para las tres muestras de arcilla en estudio y para los dos colorantes empleados.
2.5 Efecto de la concentración inicial del colorante y de la cantidad de arcilla en la remoción del color
Para estudiar el efecto que tiene la concentración inicial del colorante y la cantidad de arcilla se prepararon seis muestras de 25 mL de agua coloreadas, dos con una concentración de colorante igual a 80, 40 y 20 (mg/L). Se mantuvo la temperatura constante a temperatura ambiente. Para estudiar el efecto de la cantidad de arcilla se usó 0.15 g y 0.30 g de arcilla. Se midió la absorbancia óptica de cada una de las soluciones una vez transcurrido un tiempo de contacto igual a 15, 30, 60 y 120 min en agitación.
2.6 Estudio del mecanismo de adsorción del colorante catiónico y Aniónico
Las isotermas de adsorción son importantes para describir la interacción de los colorantes con el adsorbente y de gran utilidad para determinar la capacidad adsorbente de diferentes materiales. En este trabajo se emplearon en particular los modelos de adsorción de Langmuir, Freundlich, Tempkin y Dubinini-Radushkevich. Para verificar la aplicabilidad del modelo de adsorción, se procedió a ajustar una línea recta a los puntos experimentales. El ajuste con el mayor valor de R 2 sugirió el mecanismo de adsorción imperante.
La isoterma de adsorción describe la adsorción de una molécula (átomo) en una superficie a temperatura constante. La isoterma de adsorción representa la cantidad de moléculas (átomos) que se han adsorbido (ligado) en la superficie de un adsorbente como una función de la cantidad de moléculas presentes en solución. Los parámetros que describen la isoterma de adsorción son útiles para el diseño de sistemas de adsorción (Mahmoodi, Salehi, & Arami, 2011).
Langmuir postuló que cuando se inicia la adsorción, cada molécula que incide sobre la superficie se puede ligar a la superficie (adsorber), pero al continuar este proceso, se puede esperar que solo se ligan a la superficie (adsorben) aquellas moléculas que inciden en sitio disponibles (no ocupados todavía). También, Langmuir postuló que las moléculas adsorbidas se pueden desligar de la superficie (desorber) por agitación térmica. Cuando la velocidad de adsorción y desorción son iguales se alcanza el equilibrio adsorción-desorción. Así, la ecuación de Langmuir se dedujo asumiendo que: (1) existe un número fijo de sitios activos disponibles para la adsorción y que la energía de adsorción en cada uno de estos sitios es la misma (homogénea), (2) que sólo se puede formar una monocapa de moléculas del adsorbato en la superficie del adsorbente y que no existe interacción entre las moléculas adsorbidas, y (3) que la adsorción es reversible y alcanza la condición de equilibrio adsorción-desorción. La expresión en la ecuación (4) representa la isoterma de Langmuir.
En la ecuación (4), q e (mg/g) es la cantidad de miligramos de adsorbato que se encuentra adsorbido por gramo de adsorbente cuando se alcanza el equilibrio; C e (mg/L) es la concentración del adsorbato en solución cuando se ha alcanzado el equilibrio; q m (mg/g) es la cantidad de adsorbato necesaria para forma una monocapa en la superficie (capacidad de adsorción); K L (L/mg) es la constante de Langmuir. La magnitud de la constante de Langmuir es mayor cuanto mayor sea la energía de ligadura y menor sea la temperatura (Budnyak, et al., 2019).
La ecuación (4) se puede rescribir como se muestra en la ecuación (5), así, al graficar 1/q e como una función de 1/C e se obtiene una línea recta cuya intercepción con eje “y” es igual a 1/q m y su pendiente es igual a 1/(K L q m ).
Weber & Chakravorti (1974) definieron la constante adimensional R L que se conoce como factor de separación y que tiene la forma que se muestra en la ecuación (6).
En la ecuación (6), C 0 (mg/L), es la concentración inicial del adsorbato. El valor del R L es mayor que 1 cuando la adsorción no es favorable, es igual a 1 cuando la adsorción es lineal, se encuentra entre 0 y 1 cuando la adsorción es favorable, y es igual a cero cuando la adsorción es irreversible.
Isoterma de Freundlich
La isoterma de Freundlich considera las heterogeneidades de la superficie y lleva implícita la hipótesis de que la adsorción ocurre en sitios con diferentes energías de adsorción y que no ocurre asociación ni disociación de moléculas. La energía de adsorción varía como una función del cubrimiento. Esta isoterma también se aplica a la adsorción de múltiples capas y ha sido ampliamente aplicada en sistemas de adsorción heterogéneos, especialmente aquellos que involucran compuestos orgánicos y especies sobre carbón activado. La isoterma de Freundlich se puede expresar como se muestra en la ecuación (7).
En la ecuación (7), K F , se denomina constante de Freundlich y esta relaciona con la capacidad de adsorción; n representa el factor de heterogeneidad y 1/n está relacionada con la intensidad de adsorción. Si el valor de 1/n es igual a cero la adsorción es irreversible, si 1/n es igual a uno la isoterma de adsorción es lineal, si está entre cero y uno la adsorción es favorable y ocurre de manera normal, y si es mayor a uno la adsorción no es favorable e indica que la adsorción ocurre de manera cooperativa. La ecuación (7) se puede rescribir como se muestra en la ecuación (8) (Dada, Olalekan, Olantunya, & Dada, 2012; Saini, Garg, & Gupta, 2018).
Cuando se grafica el log10(q e ) en función del log10(C e ) se obtiene una línea recta que exhibe una intercepción con el eje “y” igual a log10(K F ) y pendiente igual a (1/n).
La isoterma de Freundlich tiene como desventaja que, de acuerdo con la ecuación, la cantidad adsorbida incrementa infinitamente con el incremento de la concentración y no predice la saturación asintótica del adsorbente a alta concentración de partículas adsorbidas, ni se reduce al comportamiento lineal a baja concentración de este. Por lo que su rango de aplicabilidad real se reduce a un intervalo determinado de concentración (Saini et al., 2018).
Isoterma de Temkin
El modelo de adsorción de Temkin se caracteriza por: (1) asumir que el calor de adsorción disminuye linealmente -antes que logarítmicamente, como se asume en el modelo de adsorción de Freundlich- con la temperatura, (2) considerar explícitamente las interacciones entre el adsorbente-adsorbato y (3) distribución uniforme de las energías de enlace (hasta una energía de enlace máxima). El modelo de isoterma de Temkin se expresa como se muestra en la ecuación (9).
En la ecuación (9), B T =RT/b (J/mol), representa una constante relacionada con el calor de adsorción; R (J/mol K), simboliza la constante universal de los gases y es igual a 8.314; T (K), representa la temperatura a la cual se está realizando el experimento; b, representa una constante adimensional; A T (L/g), es una constante de ligadura en el equilibrio. Los valores de B T y A T , se determinan graficando q e en función del ln(C e ) (Abdeen & Mohammad, 2014; Dada et al., 2012).
Isoterma de Dubinin-Radushkevich
La isoterma de Dubinin-Radushkevich considera la adsorción sobre una superficie heterogénea y que la distribución de valores de energía de adsorción tiene la forma de una gaussiana. El modelo de isoterma de Dubinin-Radushkevich se expresa como se muestra en la ecuación (10).
y 
,
En la ecuación (10), A DR (mol2/kJ2), representa una constante; ( (kJ/mol), simboliza el potencial de Polanyi. El valor de A DR y q m se pueden obtener al graficar el ln(q e ) en función de los valores de (2. La pendiente de la línea recta será igual al valor de A DR y la intercepción con el eje “y” conducirá al valor de q m .
Este modelo permite calcular la energía de adsorción -energía necesaria para llevar una molécula desde el infinito en la solución a que se encuentra adsorbida en la superficie- usando la expresión en la ecuación (11).
El valor de E es útil para estimar el tipo de proceso de adsorción. Si el valor se encuentra entre 8 y 16 kJ/mol el proceso de adsorción ocurre a través de un mecanismo de intercambio de iones (quimi-adsorción). Si el valor es menor a 8 kJ/mol el proceso ocurre a través de una adsorción física (fisi-adsorción).
Una de las características únicas del Dubinin-Radushkevich es que este modelo de isoterma se basa en el hecho de que depende de la temperatura, al graficar el ln(q e ) en función de los valores de (2 para todos los valores de temperatura, se obtienen una sola curva, denominada curva característica (Dada et al., 2012; Elmoubarki et al., 2015).
2.7 Estudio de la Cinética de adsorción del colorante catiónico y Aniónico
Los estudios de la cinética de adsorción permiten obtener información relacionada con la eficacia y eficiencia del proceso de adsorción y la viabilidad del escalamiento de las operaciones (Calvete, Lima, Cardoso, Dias, & Pavan, 2009). La cinética de adsorción permite determinar como varía con el tiempo la interacción de la molécula del colorante con la superficie de la partícula de arcilla. Esta información permite tener una idea de la efectividad de la arcilla en la remoción del color. Para estudiar la cinética de adsorción se verifico cuál de los siguientes modelos se ajusta mejor a los datos experimentales: pseudo primer orden, pseudo segundo orden y difusión intra-partículas. Para verificar la aplicabilidad del modelo de adsorción, se procedió a ajustar una línea recta a los puntos experimentales. El ajuste con el mayor valor de R 2 sugirió el modelo de adsorción imperante.
Cinética de adsorción de pseudo-primer orden
El modelo cinético de pseudo-primer orden fue propuesto por Langergren (1898) y se representa por la expresión matemática señalada en la ecuación (12).
Integrando la ecuación (9) y aplicando las condiciones de frontera: q t = 0 cuando t = 0 y q t = q t cuando t = t, se obtiene:
Rescribiendo la ecuación (13), obtenemos:
En la ecuación (14), q t (mg/g), es la cantidad de miligramos de adsorbato que se encuentra adsorbido por gramo de adsorbente en un tiempo t; k 1 (min-1), representa la constante de velocidad de adsorción. El valor de k 1 se obtiene al graficar el log10(q e -q t ) en función de t.
Cinética de adsorción de pseudo-segundo orden
El modelo cinético de pseudo-segundo orden fue propuesto por (Ho & Mckay, 1999) y se representa por la expresión matemática señalada en la ecuación (15).
Rescribiendo la ecuación (15) e integrando con las mismas condiciones de frontera que se especificaron anteriormente, obtenemos:
Rescribiendo la ecuación (16), obtenemos:
En la ecuación (17), k 2 (g/mg min), es la constante de velocidad de adsorción de pseudo-segundo orden. El valor de k 2 se obtiene al graficar t/q e en función de t. La pendiente es 1/q e y la intercepción con el eje “y” es 1/k 2 q e 2 . La velocidad de adsorción inicial es:
Modelo de difusión intrapartícula
El transporte del adsorbato desde la solución a la superficie de las partículas adsorbentes puede involucrar uno o más de los siguientes pasos: difusión del adsorbato en la solución, difusión a través de los poros, difusión en la superficie de la partícula (intrapartícula) y adsorción en la superficie, entre otros (Elmoubarki et al., 2015). Para la interpretación de los datos cinéticos experimentales desde el punto de vista de los mecanismos involucrados en el proceso de adsorción, es importante identificar qué pasos limitan y determinan la velocidad de adsorción.
El modelo de difusión intrapartícula se representa en la ecuación (19) (Weber & Morris, 1963).
En la ecuación (19), k id (mg/g min1/2) es la constante de velocidad de difusión intrapartícula y C (mg/g) es una constante que provee información acerca del espesor de la capa límite “boundary layer”. Si la gráfica de q t en función de t 1/2 conduce a una línea recta que pasa por el origen, el proceso es fuertemente influenciado por la difusión intrapartícula. Si la línea no pasa por el origen, entonces la difusión intrapartícula no es el único paso que limita la velocidad de adsorción (Abdeen & Mohammad, 2014; Saini et al., 2018).
Resultados y Discusión
Caracterización de las arcillas
La composición química elemental de las arcillas se muestra en la tabla 1. El contenido de SiO2 es de 65.74 % en la arcilla SH, es algo mayor que los adsorbentes de CO y SC, que mostraron unos porcentajes de 39.95% y 57.82%, respectivamente. La cantidad de Al2O3 del adsorbente de SH 16.99 %, es menor que los porcentajes de los adsorbentes de SA 22.71% y 25.57 % de CO, respectivamente.
Con respecto al Fe2O3 es considerado un agente colorante común en las arcillas por lo que el adsorbente de CO presenta 21.21% lo que le atribuye un color rojizo a la arcilla en comparación con los adsorbentes de SC y SH que por su bajo porcentaje presentan una coloración blanquecina. El contenido de potasio K2O en la arcilla de SC, es atribuido a su presencia en el espaciado interlaminar como catión de intercambio.
La relación de Si/Al controla la capacidad de intercambio catiónico, ya que si el Si es sustituido por Al aumentan las cargas negativas en las partículas de arcilla y estas pueden atraer cationes (cargas positivas) (Carretero & Pozo, 2007; Fassbender & Bornemisza, 1987). En los análisis realizados, observamos que la relación SiO2/Al2O3 es mayor en SH>SC> CO. Lo que nos permite concluir que la arcilla de SH tiene más cargas negativas por la sustitución isomórfica que ocurre cuando el Al+3 sustituye al Si+4, con respecto a las arcillas provenientes de CO y SC.
Tabla 1: Análisis químico por FRX de los adsorbentes.
| Valores expresados en % en peso | ||||||
| Conchacay | Santa Clara | Shirahuan | ||||
| SiO2 | 39.95 | 57.82 | 65.74 | |||
| Al2O3 | 25.57 | 22.71 | 16.99 | |||
| Fe2O3 | 21.21 | 1.17 | 7.89 | |||
| SO3 | 0.11 | 0.02 | 0.02 | |||
| K2O | 0.14 | 2.03 | 0.16 | |||
| TiO2 | 2.09 | 1.03 | 0.42 | |||
| MgO | 1.23 | 0.78 | - | |||
| CaO | 0.40 | 0.40 | 1.09 | |||
| MnO | 0.35 | 0.06 | 0.01 | |||
En la tabla 2 se observa que las arcillas naturales exhiben valores de pH en KCl menores que pH en H2O y el ΔpH es negativo, este resultado sugiere que las arcillas a pH de campo poseen cargas negativas en su superficie y que poseen una capacidad intrínseca de atraer cargas positivas (cationes), la condición inversa ocurre cuando el ΔpH es positivo y la arcilla exhibe capacidad de atraer cargas negativas (aniones) (Fassbender & Bornemisza, 1987). La diferencia entre pH medido en KCl y el pH medido en agua, es igual a delta pH (∆Ph).
∆Ph = pH KCl - pH H2O,
∆ pH > 0 indica predominio de carga positiva,
∆ pH = 0 indica carga neutra,
∆ pH < 0 indica predominio de carga negativa.
Las arcillas con predominio de cargas negativas se han denominado arcillas catiónicas, ya que exhiben capacidad de adsorber colorantes catiónicos. En la naturaleza las arcillas aniónicas no son tan frecuente como las catiónicas. Sin embargo, son económicas y fáciles de sintetizar (Aid et al., 2017). De la tabla 2 podemos señalar que la arcilla de SH presenta una superficie con una mayor cantidad de cargas negativas teniendo un potencial para adsorber colorantes catiónicos.
Tabla 2: Valoresde pH y ΔpH para las arcillas.
| Arcilla | Valores de pH | |||
|---|---|---|---|---|
| pH KCl | pH H2O | ΔpH | ||
| Conchacay | 4.85 | 5.20 | - 0.35 | |
| Santa Clara | 4.21 | 5.04 | - 0.83 | |
| Shiraguan | 4.41 | 7.28 | - 2.87 | |
En la figura 3 se muestran los difractogramas de las tres muestras en estudio. Se puede apreciar que las muestras están constituidas por una mezcla de una variedad de compuestos. Sin embargo, la arcilla de CO contiene mayores cantidades (alrededor de 60%) de arcilla tipo 1:1 (Caolinita), en contraste con el contenido de arcilla tipo 2:1 (Illita) que es de 33%. La muestra de SC está conformada por un 57% de arcilla tipo 1:1 (Caolinita), un 16% de arcilla tipo 2:1 (Illita), un 17% de arcilla tipo 2:1 (pirofilita) y un 8% de fase minerales primarias. La muestra de SH exhibe mayor cantidad (51%) de arcilla tipo 2:1 (Illita), un 8% de arcilla tipo 1:1 (Caolinita) y un 40% de fase minerales primarias. Estos resultados permiten señalar que la arcilla de SH al tener una mayor cantidad de arcillas de tipo 2:1 va a tener una mayor superficie específica y una mayor capacidad de intercambio catiónico que se traduce en una mayor cantidad de cargas negativas activas (Bergaya & Lagaly, 2013).
Colorante catiónico Basic Azul Marino 2RN
El efecto del pH es el factor más esencial que controla el proceso de adsorción porque afecta tanto la carga de la superficie del adsorbente como el grado de ionización de los grupos funcionales del adsorbato, así como, el mecanismo de adsorción (Elmoubarki et al., 2015).
En la figura 4, se muestran los resultados del efecto del pH en la remoción de el colorante (CC) usando las tres arcillas bajo estudio. La arcilla de CO mostró una mayor remoción cuando el valor del pH es igual a 6, con aproximadamente un 98%, y se mantiene en un 95%, a pH 10, la remoción disminuye aproximadamente a 88 % a pH 12. En la figura 4, se observa que la arcilla de SC presenta un comportamiento similar presentado los mayores valores de remoción entre el pH de 2 a 4 y disminuyó a pH 12. La arcilla de SH presentó un comportamiento diferente y el valor de remoción mostró un aumento en la medida que el pH vario de 2 a 12. Presentando una remoción del 99 % a pH 12.
Figura 4: Efecto del pH en la efectividad de las arcillas en la remoción del colorante catiónico Basic Azul Marino 2RN. Condiciones: 15 min, 80 ppm, 20 ºC, V=50 mL, 0.30 gr de arcilla.
Se puede apreciar en la figura 4, que la efectividad en la remoción del colorante se reduce en las arcillas de CO y SC si el pH es de 12, mientras que incrementa en la arcilla de SH cuando el pH es 12. Lo inverso ocurre cuando el pH es 2, la arcilla con menor efectividad removiendo el color es la de SH. Este comportamiento está relacionado con la carga superficial de las arcillas en el caso de CO y SC adquiere una mayor cantidad de cargas negativas a pH menores de 6.2, mientras que la carga superficial de la arcilla SH es más negativa a pH> 6.
3.2.2 Colorante aniónico Drimaren Amarillo CL-2R
La figura 5 muestra el efecto del pH con el agua coloreada de la arcilla CO, SC y SH, respectivamente. En la figura se observa que las tres arcillas tienen un comportamiento similar la mayor remoción ocurre a pH 2 siendo esta de 47% para la arcilla de SC, 40% para CO y 23 % para SH respectivamente. Esta remoción disminuye a menos del 5% a partir del pH de 6 a 10.
Esta disminución se debe a que al disminuir el pH a 2 se crea una película protónica de iones H+, que producirán atracción a las moléculas del colorante que están cargadas negativamente, lo cual en el presente caso genera una eficiencia de remoción semejante al 47% para pH de 2. Sin embargo, cuando la situación cambia y el potencial de hidrógeno aumenta, la eficiencia de remoción (%) se ve notablemente afectada, pues decrece hasta alcanzar tan solo menos del 5% aproximadamente a pH de 10. La razón de este descenso abrupto, se debe a que los iones negativos aumentan, pues habrá una mayor cantidad de OH- en la solución, los cuales competirán con los aniones del colorante por los sitios activos (Das et al., 2019; Malakootian et al., 2014).
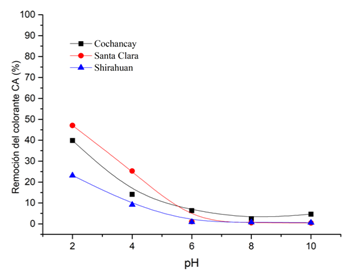
Figura 5: Efecto del pH en la efectividad de las arcillas en la remoción del colorante aniónico Drimaren Amarillo CL-2R. Condiciones: 15 min, 80 ppm, 20 ºC, V=50 mL, 0.30 gr de arcilla.
En a la figura 6 también se muestra el efecto del tiempo de contacto del colorante CA con la arcilla. En la figura 6 se observa que el equilibrio se alcanza a los 30 min de contacto del adsorbato con la arcilla de CO y SC y que la interacción con adsorbato-adsorbente está siendo fuertemente mediada por la concentración del adsorbato cuando la concentración en mayor a 60 mg/L. La figura 6 muestra que otros efectos diferentes a la interacción adsorbato-adsorbente están mediando el equilibrio, en particular cuando la concentración del adsorbato es de 80 mg/L. La capacidad de adsorción fue más baja para la arcilla de SC siendo de aproximadamente 3.5 mg/g.
Efecto de la concentración inicial de colorante
Las figuras 7a, 7b y 7c, muestran el efecto de la concentración inicial del CC en la efectividad de las arcillas removiendo colorantes catiónicos. El eje “y” a la izquierda representa la remoción (%) y corresponde a la traza negra y el eje “y” de la derecha representa la capacidad de adsorción en el equilibrio qe (mg/g).
En la figura 7a para la arcilla de CO, se observa que la remoción incrementa en la medida que incrementa la concentración del colorante. Este resultado sugiere que la interacción entre adsorbato y adsorbente es mayor a medida que incrementa la concentración del adsorbato, incrementando la probabilidad de adsorción en la arcilla de CO. Mientras que en las figuras 7b y 7c, se muestra que la eficacia de las arcillas de SC y SH no se ve afectada por el incremento en la concentración del colorante catiónico.
La capacidad de adsorción representada en el eje y de la parte derecha podemos observar que en las tres arcillas la capacidad de adsorción aumento desde 2 mg/g a concentraciones de 20 mg/L hasta una capacidad de adsorción de 6 mg/L a la concentración de 80 mg/L.
Las figuras 7d, 7e y 7f, muestran el efecto de la concentración inicial del colorante CA en la eficacia de las arcillas removiendo colorantes aniónicos. En las figuras 7d y 7e, se observa que en las arcillas de CO y SC la eficacia de la remoción es alta cuando la concentración del colorante es de 20 ppm, sin embargo, esta eficacia se reduce sustancialmente cuando la concentración del colorante es de 80 ppm. Este resultado sugiere que existe una saturación de los sitios activos en la superficie de los adsorbentes, sugiriendo una adsorción en monocapas como la del modelo de Langmuir. El efecto de saturación se puede observar en la figura 7f correspondiente a la arcilla de SH. En esta última figura se hace notable la baja eficacia que tiene la arcilla de Shirahuan para remover colorantes aniónicos, posiblemente debido a la existencia de muy pocos sitios activos en su superficie.
Efecto de la cantidad de arcilla
Las figuras 8a, 8b y 8c muestran el efecto de la cantidad de arcilla en la remoción del colorante CC. Mientras que, en las figuras 8d, 8e y 8f, muestran el efecto de la cantidad de arcilla en la remoción del colorante CA. En la figura 8a se aprecia que en la medida que incrementa la cantidad de arcilla ocurre un ligero descenso en el porcentaje de remoción del colorante catiónico representado la traza de color negro. Este resultado sugiere una interacción débil entre adsorbato-adsorbente. Sin embargo, la remoción se mantiene por arriba del 85%. En las figuras 8b y 8c, se aprecia que en la medida que incrementa la cantidad de arcilla el porcentaje de remoción incrementa y se estabiliza en alrededor del 100%. Este resultado sugiere que en la medida que incrementa los sitios activos en las tres arcillas incrementa la probabilidad de adsorción hasta que se ocupan todos los sitios cuando la concentración es alrededor de 0.15 g/100 mL.
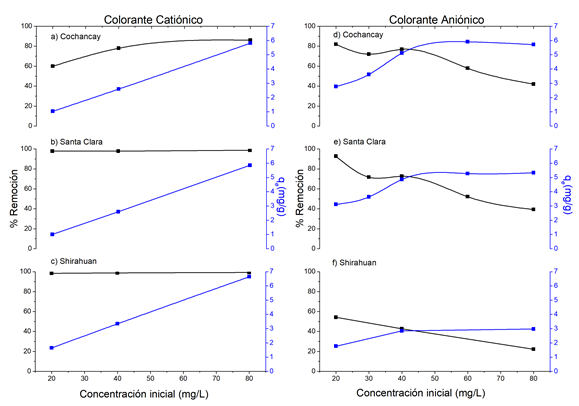
Figura 7: Efecto del tiempo de concentración del colorante Basic Azul Marino 2RN (CC) y Drimaren Amarillo CL-2R (CA). Condiciones: para el CC se usó un pH de 8 y para el CA un pH de 2, 0.3g de arcilla, 20ºC, V=50 mL. El eje “y” a la izquierda representa la remoción (%) y que corresponde a la traza negra y el eje “y” derecha representa el q e (mg/g).
En las figuras 8d, 8e y 8f se puede observar el efecto de la cantidad de arcilla en el porcentaje de remoción del CA. En las tres figuras se observa que en la medida que incrementa la densidad de sitios activos (cantidad de arcilla) el porcentaje de remoción incrementa en correspondencia con un incremento en la probabilidad de adsorción. De las tres arcillas, la de CO muestra mayor eficacia (70%) en la remoción del colorante aniónico cuando la cantidad de arcilla es de 0.30 g/mL. La capacidad de adsorción aumenta desde 2.5 mg/g hasta 4.5 mg/g duplicando su capacidad de adsorción cuando se usa 0.3g/L de arcilla.
Figura 8: Efecto de la cantidad de arcilla en el colorante Basic Azul Marino 2RN (CC) y Drimaren Amarillo CL-2R (CA). Condiciones: para el CC se usó un pH de 8 y para el CA un pH de 2, 20ºC, V=50 mL. El eje “y” a la izquierda está representado la Remoción (%) y el eje Y derecha el qe(mg/g) que representa la capacidad de adsorción en el equilibrio.
Isotermas de adsorción
Los resultados del análisis del mecanismo de adsorción imperante en cada uno de los ensayos realizados con el CC y las arcillas de CO, SC y SH son mostrados en la tabla 3. Como es conocido, los coeficientes de correlación R2 permiten determinar el modelo de equilibrio que mejor se ajuste con los datos experimentales.
Tabla 3: Resultados del ajuste de los modelos de isotermas de adsorción del colorante catiónico Basic Azul Marino 2RN. Condiciones experimentales: pH=10, V=25 mL, 0.30 g de arcilla, t c =120 min.
Los resultados de la tabla 3 señalan que el modelo de Langmuir es el que mejor se ajusta a los datos experimentales para la arcilla de SH seguida de la arcilla de SC con un valor de R2 de 0.998 y 9.736 respectivamente. Los valores del parámetro de Langmuir, q m describe la capacidad de saturación de la superficie del material adsorbente en el equilibrio. Los valores de adsorción máximas (q m ) fueron: 27.530 mg/g (SH) y 12.725 mg/g (SC). De la tabla 2, se puede concluir que, en la arcilla de SH, se presenta la mayor afinidad entre el adsorbato y el sitio activo del adsorbente con un K de 0.806.
La razón que la arcilla SH tenga una mayor capacidad de adsorción, se debe a que los iones negativos aumentan, pues habrá una mayor cantidad de OH- en la solución (Das et al., 2019; Malakootian et al., 2014) aumentando una mayor superficie de sitios activos.
Esta mayor capacidad de adsorción de la arcilla de SH es confirmada con los datos de la caracterización de las arcillas, los datos de rayos X que confirman que esta arcilla tiene una mayor cantidad de arcillas de tipo 2:1 las cuales se caracterizan por tener una mayor superficie específica y mayor cantidad de cargas negativas como se confirmó en la evaluación del ∆pH.
El modelo de adsorción que más se ajustó a los datos experimentales para la arcilla de CO, es el Tempkin, con un R2 fue de 0.99. El modelo de isoterma de Temkin asume que el calor de adsorción disminuye linealmente en todas las capas del adsorbente debido a las posibles interacciones adsorbato-adsorbente, y esta adsorción se caracteriza por ser uniforme sobre toda la superficie de contacto (Saini et al, 2018). La constante de Temkin B T (J/mol), representa una constante relacionada con el calor de adsorción, si esta es menor de 8 (kJ/mol) indica que existe una interacción débil entre el colorante y la arcilla y el fenómeno se describe mejor mediante una adsorción en superficie homogénea. Los valores obtenidos de la isoterma de Tempkin fueron K T = 2.0 L/g: y el B T fue de 0.84 kJ/mol < 8 (kJ/mol) y así el mecanismo involucrado es la adsorción física (fisisorción). En el proceso de fisisorción, los adsorbatos se adhieren al adsorbente a través de una débil interacción de Van der Waals y, por lo tanto, este proceso está asociado con energías relativamente bajas (Araújo et al, 2018).
En la tabla 4, se muestran los resultados del análisis del mecanismo de adsorción dominante en cada uno de los ensayos realizados con el CA y las arcillas de CO, SC y SH. En esta tabla, se aprecia que el modelo de Langmuir se ajusta muy bien a los datos experimentales (R2>0.943) en las tres arcillas estudiadas.
Tabla 4: de isotermas de adsorción del colorante aniónico Drimaren Amarillo CL-2R. Condiciones experimentales: pH=2, V=25 mL, 0.30 g de arcilla, t c =120 min.
| Modelo | Valores Parámetros | Conchacay | Santa Clara | Shirauam |
|---|---|---|---|---|
| Langmuir | q m | 5.814 | 3.189 | 1.067 |
| K L (L/mg) | 0.343 | 4.591 | 8.673 | |
| R L | 0.062 | 0.002 | 0,001 | |
| R2 | 0.977 | 0.943 | 0.972 | |
| Freundlich | K F (mg/L) | 1.762 | 2.453 | 0.807 |
| 1/n | 2.866 | 6.894 | 2.113 | |
| R2 | 0.890 | 0.678 | 0.866 | |
| Tempkin | K T (L/mg) | 0.002 | 0.053 | 0.053 |
| B T (J/mol) | 19386 | 57551 | 22919 | |
| R2 | 0.874 | 0.780 | 0.869 |
Lo que sugiere que el colorante aniónico se adsorbe homogéneamente mediante interacción electrostática con la superficie y esta adsorción se encuentra asegurada debido a que la superficie de las arcillas se encuentra cargada positivamente. Así, de la tabla 4, se puede concluir que la capacidad de adsorción o cantidad de adsorbato necesario para formar un monocapa para la arcilla de CO, SC y SH es de 5.814 mg/g, 3.819 mg/g y 1.067 mg/g de arcilla, respectivamente. En todos los casos el valor del R L se encuentra entre 0 y 1, lo que indica que la adsorción es favorable y reversible.
Cinética de adsorción
La cinética de adsorción permite determinar la rapidez con la cual el colorante interacciona con la superficie adsorbente para su remoción; es una de las características importantes que definen la eficiencia de un adsorbente. Los parámetros de los modelos pseudo segundo orden y del modelo de difusión intra-partícula se muestra en la tabla 5. Los valores del modelo de pseudo primer orden no se reportan porque los valores del R2 fueron bajos.
Los resultados de la tabla 5 confirman que la adsorción de los CC en las tres arcillas estudiadas sigue un comportamiento descrito en el modelo cinético de pseudo-segundo orden, con un valor de R2 mayor a 0.99. Esta expresión matemática se basa en la capacidad de adsorción en equilibrio y asume que la velocidad de adsorción es directamente proporcional al cuadrado de sitios disponibles (Halbus, Athab y Hussein, 2013). Se logró una diferencia muy baja entre q e(exp) y q e(cal) en la cinética de pseudo segundo orden, que indicaba el mejor ajuste de la adsorción de CO, SC y SH con el CC.
En la tabla 5, se observa que a la concentración de 80 mg/g y una cantidad de arcilla de 0.05g se alcanza la capacidad máxima de adsorción qe(exp) del colorante catiónico fue de 40.2 mg/g, 38.5 mg/g y 36.0 mg/g para la arcilla de CO, SC y SH respectivamente. Mientras que la velocidad de adsorción inicial (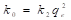
) del colorante catiónico fue de 17.8 g/mg min, 19.8 g/mg min y 27.4 g/mg min para la arcilla de CO, SC y SH, respectivamente.
En las figuras 9a, 9b y 9c, se muestra el ajuste de los datos experimentales al modelo cinético de pseudo-segundo orden en los ensayos realizados con el CC.
Los parámetros de los modelos cinéticos pseudo segundo orden y del modelo de difusión intra-partícula del CA en la superficie de arcilla de CO, SC y SH se muestran en la tabla 6 el modelo cinético pseudo-segundo orden es que el mejor se ajusta a los datos experimentales con un valor de R2 mayor a 0.99. Allí se observa que a la concentración de 80 mg/g y una cantidad de arcilla de 0.05 g se alcanza el mayor valor de capacidad máxima de adsorción q
e
del colorante aniónico de 5.90 mg/g, 5.27 mg/g y 5.47 mg/g para la arcilla de CO, SC y SH, respectivamente. Mientras que la velocidad de adsorción inicial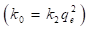
del colorante aniónico fue de 9.49 g/mg min, 2.86 g/mg min y 4.09 g/mg min para la arcilla de CO, SC y SH, respectivamente. De manera similar, los resultados sugieren que las arcillas de SC y SH tienen valores máximos similares de velocidad de adsorción del colorante aniónico (5.47 g/mg min). Mientras que la arcilla de CO exhibió la mayor velocidad de adsorción inicial de colorante aniónico (9.5 g/mg min).
En las figuras 10a, 10b y 10c, se muestra el ajuste de los datos experimentales al modelo cinético de pseudo-segundo orden en los ensayos realizados con el colorante aniónico.
Los datos en las tablas 5 y tabla 6 muestran que la bondad del ajuste del modelo de difusión intra-partícula a los datos experimentales es relativamente alto, con un valor de R2 > 0.90 en la mayoría de los casos y en la adsorción tanto del colorante catiónico como aniónico. Este resultado sugiere que la difusión intra-partícula está involucrada en la cinética de adsorción. El valor de la constante C (mg/g) que provee información acerca del espesor de la capa límite “boundary layer”. El valor máximo de C en el ensayo con el colorante catiónico fue 31.2 mg/g, 37.4 mg/g y 30.9 mg/g para la arcilla CO, SC y SH respectivamente. Mientras que para el colorante aniónico fue 1.8 mg/g, 2.0 mg/g, 3.2 mg/g para la arcilla CO, SC y SH, respectivamente.
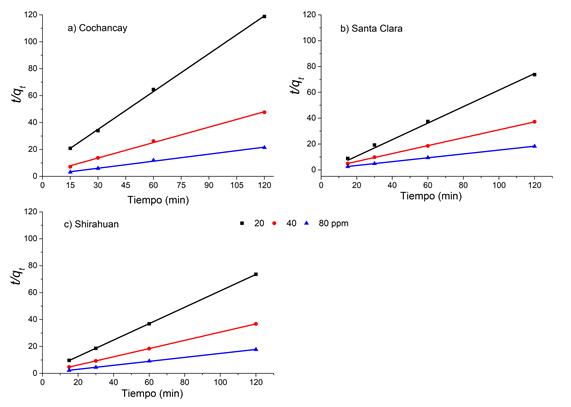
Figura 9: Cinética de pseudo-segundo orden para el colorante catiónico, Basic Azul Marino 2RN. Condiciones experimentales: pH=10, V=25 mL, 0.30 g de arcilla, tc=120 min.
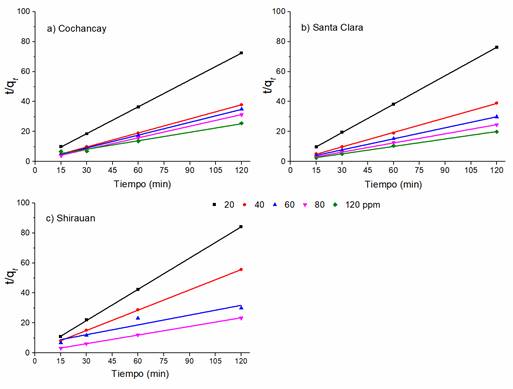
Figura 10: Cinética de pseudo-segundo orden para el colorante aniónico, Drimaren Amarillo CL-2R. Condiciones experimentales: pH=10, V=25 mL, 0.30 g de arcilla, tc=120 min.
Tabla 5: Parámetros del modelo cinético de adsorción del colorante Basic Azul Marino 2RN. Condiciones experimentales: pH=10, V=25 mL, 0.05 a 0.30 g de arcilla, tc=120 min.
| Arcillas | Gramos | Colorante | PSEUDO SEGUNDO ORDEN | DIFUSIÓN INTRA-PARTÍCULA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (g) | (mg/L) | q e(cal) | K 2 | q e(exp) | R2 | k id | C | R2 | |||
| (mg/g) | (g/mg min) | (mg/g) | (mg/g min0.5) | (mg/g) | |||||||
| Cochancay | 0.05 | 20 | 8.475 | 0.032 | 8.231 | 0.999 | 0.175 | 6.426 | 0.884 | ||
| 40 | 18.563 | 0.025 | 18.175 | 0.997 | 0.286 | 14.888 | 0.876 | ||||
| 80 | 40.274 | 0.011 | 39.206 | 0.998 | 0.715 | 31.188 | 0.976 | ||||
| 0.10 | 20 | 4.031 | 0.113 | 3.976 | 0.999 | 0.043 | 3.501 | 0.934 | |||
| 40 | 9.031 | 0.049 | 8.809 | 0.998 | 0.147 | 7.135 | 0.917 | ||||
| 80 | 18.292 | 0.027 | 18.084 | 0.999 | 0.154 | 16.529 | 0.783 | ||||
| 0.15 | 20 | 2.887 | 0.075 | 2.795 | 0.998 | 0.056 | 2.174 | 0.832 | |||
| 40 | 6.214 | 0.060 | 6.068 | 0.999 | 0.122 | 4.879 | 0.527 | ||||
| 80 | 12.575 | 0.033 | 12.302 | 0.999 | 0.223 | 10.128 | 0.614 | ||||
| 0.30 | 20 | 1.058 | 0.148 | 1.010 | 0.999 | 0.033 | 0.665 | 0.821 | |||
| 40 | 2.718 | 0.054 | 2.611 | 0.993 | 0.069 | 1.826 | 0.932 | ||||
| 80 | 5.937 | 0.052 | 5.831 | 0.998 | 0.078 | 4.920 | 0.850 | ||||
| Santa Clara | 0.05 | 20 | 9.472 | 0.101 | 9.638 | 0.999 | 0.060 | 8.769 | 0.874 | ||
| 40 | 19.212 | 0.026 | 18.426 | 0.999 | 0.283 | 15.884 | 0.856 | ||||
| 80 | 38.521 | 0.013 | 35.430 | 0.999 | 0.098 | 37.387 | 0.683 | ||||
| 0.10 | 20 | 4.277 | 0.115 | 4.840 | 1.000 | 0.058 | 3.619 | 0.748 | |||
| 40 | 9.238 | 0.050 | 9.424 | 0.999 | 0.218 | 6.652 | 0.907 | ||||
| 80 | 19.639 | 0.024 | 19.331 | 1.000 | 0.037 | 19.226 | 0.785 | ||||
| 0.15 | 20 | 3.206 | 0.518 | 3.305 | 0.999 | 0.016 | 3.030 | 0.425 | |||
| 40 | 6.646 | 0.175 | 6.592 | 0.999 | 0.042 | 6.180 | 0.571 | ||||
| 80 | 13.205 | 0.114 | 13.185 | 0.999 | 0.056 | 12.555 | 0.881 | ||||
| 0.30 | 20 | 1.638 | 0.499 | 1.639 | 0.999 | 0.011 | 1.507 | 0.963 | |||
| 40 | 3.258 | 0.765 | 3.299 | 1.000 | 0.008 | 3.161 | 0.899 | ||||
| 80 | 6.571 | 0.451 | 6.623 | 0.999 | 0.012 | 6.427 | 0.883 | ||||
| Shirahuan | 0.05 | 20 | 9.683 | 0.179 | 9.401 | 1.000 | 0.042 | 9.219 | 0.646 | ||
| 40 | 18.580 | 0.028 | 18.858 | 0.999 | 0.122 | 17.085 | 0.989 | ||||
| 80 | 35.997 | 0.014 | 38.412 | 0.999 | 0.432 | 30.896 | 0.939 | ||||
| 0.10 | 20 | 4.879 | 0.198 | 4.206 | 0.999 | 0.038 | 4.462 | 0.503 | |||
| 40 | 9.525 | 0.054 | 8.913 | 0.999 | 0.069 | 8.674 | 0.935 | ||||
| 80 | 19.425 | 0.025 | 19.596 | 0.999 | 0.091 | 18.436 | 0.480 | ||||
| 0.15 | 20 | 3.322 | 0.369 | 3.189 | 0.999 | 0.013 | 3.157 | 0.956 | |||
| 40 | 6.630 | 0.184 | 6.602 | 0.999 | 0.034 | 6.232 | 0.735 | ||||
| 80 | 13.291 | 0.084 | 13.138 | 0.999 | 0.094 | 12.259 | 0.636 | ||||
| 0.30 | 20 | 1.646 | 1.302 | 1.625 | 0.999 | 0.005 | 1.585 | 0.779 | |||
| 40 | 3.308 | 0.640 | 3.247 | 0.999 | 0.008 | 3.213 | 0.961 | ||||
| 80 | 6.634 | 0.623 | 6.558 | 0.999 | 0.008 | 6.532 | 0.930 | ||||
Tabla 6: Parámetros del modelo cinético de adsorción del colorante Drimaren Amarillo CL-2R. Condiciones experimentales: pH=2, V=25 mL, 0.05 a 0.30 g de arcilla, tc=120 min.
| Arcilla | Gramos (g) | Colorante (mg/L) | PSEUDO SEGUNDO ORDEN | DIFUSIÓN INTRA-PARTÍCULA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| qe (mg/g) | k2 (g/mg min) | qe(exp) (mg/g) | R2 | kid (mg/g min0.5) | C (mg/g) | R2 | |||||
| Cochancay | 0.15 | 20 | 2.756 | 0.529 | 2.741 | 0.999 | 0.59827 | 0.062 | 0.999 | ||
| 30 | 3.633 | 0.263 | 3.601 | 0.999 | 0.51917 | 0.083 | 0.999 | ||||
| 40 | 5.200 | 0.131 | 5.137 | 0.999 | 0.43192 | 0.098 | 0.999 | ||||
| 60 | 5.731 | 0.136 | 5.921 | 0.999 | 0.40481 | 0.071 | 0.999 | ||||
| 80 | 5.931 | 0.197 | 5.699 | 0.999 | 0.415 | 0.048 | 0.999 | ||||
| 0.30 | 20 | 1.581 | 1.001 | 1.574 | 0.999 | 0.00553 | 1.514 | 0.978 | |||
| 40 | 3.125 | 0.671 | 3.113 | 1 | 0.01077 | 3.005 | 0.792 | ||||
| 60 | 4.073 | 0.109 | 4.004 | 0.999 | 0.05247 | 3.456 | 0.922 | ||||
| 80 | 4.907 | 0.394 | 4.886 | 1 | 0.01986 | 4.689 | 0.623 | ||||
| 100 | 5.924 | 0.108 | 5.853 | 0.999 | 0.06084 | 5.232 | 0.743 | ||||
| Shirahuan | 0.15 | 20 | 1.898 | 0.067 | 1.804 | 0.995 | 0.05618 | 1.177 | 0.987 | ||
| 40 | 3.082 | 0.028 | 2.877 | 0.981 | 0.11885 | 1.536 | 0.862 | ||||
| 80 | 3.072 | 0.063 | 2.964 | 0.998 | 0.06749 | 2.224 | 0.933 | ||||
| 0.30 | 20 | 1.452 | 0.519 | 1.463 | 0.999 | 0.01208 | 1.312 | 0.828 | |||
| 40 | 2.238 | 0.128 | 2.186 | 0.999 | 0.03629 | 1.788 | 0.999 | ||||
| 80 | 4.719 | 0.008 | 4.093 | 0.853 | 0.24907 | 1.119 | 0.773 | ||||
| 100 | 5.271 | 0.103 | 5.212 | 0.999 | 0.04206 | 4.729 | 0.910 | ||||
| Santa Clara | 0.15 | 20 | 3.126 | 0.279 | 3.106 | 0.999 | 0.01572 | 2.923 | 0.872 | ||
| 30 | 3.715 | 0.061 | 3.615 | 0.998 | 0.07297 | 2.805 | 0.902 | ||||
| 40 | 5.003 | 0.053 | 4.875 | 0.999 | 0.08975 | 3.903 | 0.995 | ||||
| 60 | 5.291 | 0.146 | 5.246 | 0.999 | 0.03359 | 4.874 | 0.973 | ||||
| 80 | 5.472 | 0.053 | 5.307 | 0.999 | 0.11116 | 4.189 | 0.754 | ||||
| 0.30 | 20 | 1.669 | 0.538 | 1.653 | 0.999 | 0.01595 | 1.499 | 0.429 | |||
| 40 | 3.182 | 0.622 | 3.168 | 0.999 | 0.0117 | 3.052 | 0.767 | ||||
| 60 | 3.874 | 0.271 | 3.849 | 0.999 | 0.01899 | 3.641 | 0.992 | ||||
| 80 | 4.243 | 0.017 | 4.634 | 0.987 | 0.25787 | 2.120 | 0.427 | ||||
| 100 | 5.121 | 0.209 | 3.400 | 0.999 | 0.02874 | 3.103 | 0.866 | ||||
Conclusiones
Las tres arcillas mostraron alta adsorción eliminando más del 90% del CC, con una capacidad de adsorción que varía para la arcilla de SH de 27.5 mg/g, SC de 17.75 mg/g y 7.32 mg/g para CO, respectivamente, esta capacidad de adsorción disminuyó a medida que el pH aumenta.
Las arcillas mostraron ser menos eficientes para remover el CA. El mecanismo de adsorción presentó un mejor ajuste mediante el modelo de Langmuir, tanto para el colorante catiónico como aniónico. La cinética de adsorción de los colorantes sigue el modelo de "pseudo-segundo orden" para ambos colorantes y sugiere que la tasa de adsorción es proporcional al cuadrado de los sitios de adsorción disponibles. Los resultados sugieren que la difusión intra-particula es un paso importante en el control de la adsorción. Las arcillas activadas muestran una capacidad de adsorción seis veces mayor eliminando el colorante catiónico que el colorante aniónico de las muestras de agua sintética.
Conflicto de Interés
Los autores declaramos que no existe conflicto de interés de naturaleza alguna en la presente investigación.
Agradecimiento
Los autores estamos agradecidos con la Dirección de Investigación de la Universidad Nacional de Chimborazo, por el respaldo a través del Proyecto Estudio de la Cinética de Adsorción de Colorantes en Arcillas Naturales. Así mismo, a el Grupo Clean Energy and Environment por el apoyo brindado a esta investigación.
