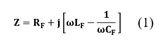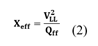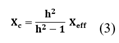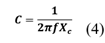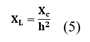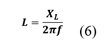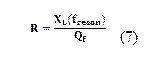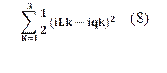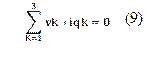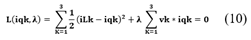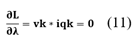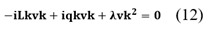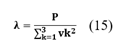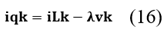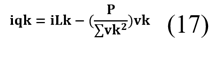INTRODUCCIÓN
En los últimos años, la incorporación de cargas no lineales al sistema ha provocado la aparición de la distorsión armónica en las redes de distribución, que está relacionada con el aumento gradual de las cargas lineales y no lineales, ha despertado un mayor interés en la creación de soluciones que solucionen este problema. La introducción de filtros de potencia activa como una técnica para reducir la distorsión en las ondas sinusoidales de voltaje y corriente se destaca en esta revisión. Para abordar el problema de los armónicos en los sistemas de distribución de energía, se han desarrollado varias estructuras, como filtros pasivos, activos, convertidores estáticos y sistemas híbridos [1].
El aumento de las cargas lineales y no lineales en los sistemas de distribución ha empeorado el problema de la tensión armónica y la distorsión de la corriente. El objetivo principal de los filtros de potencia activados es reducir la distorsión en las ondas de voltaje y corriente sinusoidales. No obstante, surge la necesidad de comprender por qué el sistema en su conjunto sufre interrupciones, lo que conduce a una propuesta de análisis más exhaustiva utilizando el modelo de distribución trifásica de la IEEE y tomando en cuenta los escenarios actuales [2].
El análisis de armónicos se vuelve importante no solo en entornos industriales, sino también en redes residenciales, tal como se muestra en Ecuador y otros lugares donde se utiliza la energía eléctrica. La presencia de corrientes o voltajes no sinusoidales, también conocidos como armónicos, puede causar problemas en el suministro eléctrico y en los dispositivos conectados a la red [3][4].
Además, se destaca que la distorsión armónica no es solo un problema en entornos industriales; también ocurre en hogares, donde las sobrecargas de fases y la distribución inadecuada son factores que contribuyen a la problemática. En este contexto, se utiliza la combinación de filtros activos de potencia para abordar situaciones particulares, como las cargas monofásicas, y se propone varias soluciones, una de las cuales es la compensación de potencia activa para equilibrar la carga en la red [5].
Se han realizado diversos estudios que buscan solucionar estos problemas mediante la mejora de la calidad de la electricidad en sistemas desequilibrados, incluyendo el balanceo de carga, el análisis de corriente de neutro, la compensación de la potencia reactiva de las cargas eléctricas y la mejora de las perturbaciones en los sistemas de potencia. Como resultado, se propone que este estudio investigue las causas armónicas de los arreglos de filtros de potencia activa y sus respectivas compensaciones [6].
La necesidad de una revisión más completa se encuentra en el centro de este estudio, ya que hay limitaciones en revisiones similares. Los filtros tradicionales y pasivos se han utilizado con éxito para reducir los armónicos. Sin embargo, la incorporación de sistemas más avanzados y métodos basados en la programación de filtros de corriente representa un paso innovador para mejorar la calidad de la electricidad en los sistemas de distribución [7].
METODOLOGÍA
Se presenta un sistema de compensación basado en el principio del filtro activo de potencia y del filtro pasivo en el cual se encargarán de compensar el THDv y THDi presentes en todo el circuito radial para que los niveles de distorsión armónica estén dentro de los niveles estandarizados de la norma ecuatoriana que rige la IEEE 519-2014 e IEC61000 y regulaciones nacionales como la resolución Nro. ARCERNNR -017/2020. Para ello se utilizó simulink para simular sistemas dinámicos y multidominio en donde podemos obtener la respuesta de circuitos eléctricos ante diferentes condiciones de carga y operación. Y dentro de esta simulación se empleó Matlab donde podemos realizar el análisis matemático avanzado y procesar las señales obtenidas del circuito, útil para el análisis de armónicos y la implementación de algoritmos de control.
Se utilizo en filtros activos de potencia la simulación EMT (Electromagnetic Transients) para simular eventos como la conmutación de cargas no lineales que pueden causar armónicos y en filtros pasivos el RMS (Root Mean Square) para evaluar el impacto global de la distorsión armónica en términos de potencia y corriente eficaz. obtenidas mediante dichas simulaciones donde se obtiene valores esperados según el modelo teórico a aplicarse para reducir los niveles de distorsión armónica de corriente y voltaje.
Dado que los filtros pasivos son dinámicos y debe ajustarse a las variaciones de carga, para las simulaciones se utilizaron valores obtenidos heurísticamente para el filtro pasivo en paralelo mientras que el filtro activo de potencia se puede controlar mediante el control programable de acuerdo a las cargas que ingresan a la red.
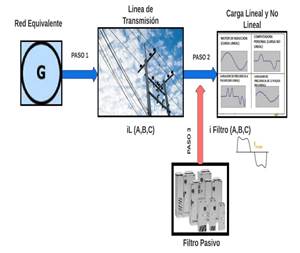
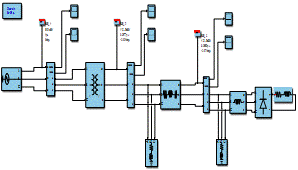
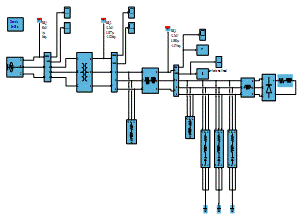
Desde la perspectiva del proceso de realizar la simulación se tomó en cuenta el diseño de la red mediante 3 etapas, Fig. 1 desde la fuente de alimentación las mediciones de distorsión armónica total de voltaje ( THD v ) y distorsión armónica total de corriente THD i se realizaron utilizando el Filtro de Transformada Rápida de Fourier (TFF) de Simulink para determinar la cantidad de distorsión armónica total de voltaje ( THD v ) y distorsión armónica total de corriente THD i introducida por el convertidor como resultado de los interruptores de potencia utilizados en cada fase donde se realiza la conexión del filtro pasivo a la red eléctrica[8][9].
Dentro del diseño del caso base a estudiar, se incorporó también un filtro activo de potencia con el objetivo de reducir considerablemente los niveles de distorsión armónica, tanto en el voltaje ( THD v ) como en la corriente ( THD i ). Esto es preferible respecto a los porcentajes de reducción logrados por el filtro pasivo. En la salida del convertidor, se instalan medidores de voltaje para verificar que el dispositivo esté generando el nivel de voltaje deseado, monitorizando la diferencia de potencial. Estos medidores son clave para determinar los niveles de potencia activa y reactiva. Además, los amperímetros se utilizan para medir las corrientes de carga y de red, complementando las mediciones de tensión mencionadas. En los lados de carga, es fundamental medir tanto la carga como las corrientes principales, además de las lecturas de voltaje mencionadas anteriormente[10].
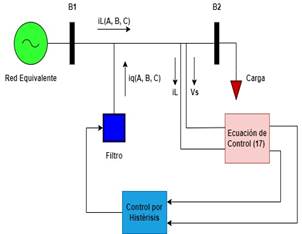
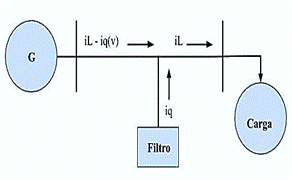
Se requieren amperímetros en la salida del convertidor de corriente para medir la corriente de entrada del filtro de potencia activo, realizando así una evaluación de monitoreo de corriente con control predictivo. Por otro lado, también se requiere un amperímetro en la salida de la fuente de corriente para mostrar la corriente actual. Donde se puede comprobar la corriente que pasa por las fases, se debe medir este parámetro. Donde se puede verificar la situación de compensación de potencia reactiva desde la perspectiva de la red en la Fig. 2 [11].
Etapa 1: Diseño del caso base
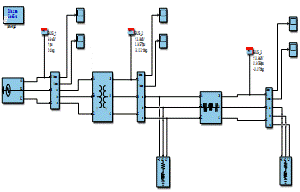
En el circuito de prueba mostrado en la Fig. 3, se presenta un sistema con una red equivalente balanceada, un transformador, tres barras y dos cargas puntuales, sin la condición de la introducción de una carga no lineal.
La red eléctrica opera a una tensión nominal de 69 kV. La línea tiene una impedancia de (0.02 + j0.1591^-3) Ω y el transformador presenta una impedancia de (0.0098+j0.0762) Ω. El sistema se compone de tres barras: la barra 1 con una tensión de 69 kV, la barra 2 con una tensión de 13.8 kV, y la barra 3 también con una tensión de 13.8 kV. En la barra 2, se encuentra una carga de 10 MW con un factor de potencia de 0.85 en atraso, mientras que en la barra 3 hay una carga de 3 MW con un factor de potencia de 0.9 en atraso. Este conjunto de componentes constituye un circuito de prueba diseñado para simular y analizar el comportamiento del sistema eléctrico bajo condiciones específicas[12].
Sistema balanceado.
En el sistema sometido a prueba, los resultados obtenidos fueron comparables a los generados mediante la creación del modelo de flujo de potencia en Simulink. Esto nos permite realizar un análisis alternativo que considera las cargas no lineales en el sistema. En la Tabla 1 se presentan los datos de la simulación del sistema balanceado sin carga no lineal.
Tabla 1: Índice de armónicos del circuito cuando no hay carga no lineal presente.
| Bus | THDv % | THDi % |
| 1 | 0.17 | 0.16 |
| 2 | 0.17 | 0.16 |
| 3 | 0.17 | 0.17 |
En relación con el análisis obtenido del orden de los armónicos presentes en el sistema del caso base, se determina la frecuencia armónica tanto del voltaje como de la corriente.
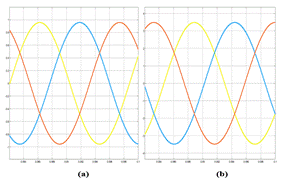
Tras realizar la prueba correspondiente al circuito del caso base, se observa que no presenta ninguna perturbación armónica en todo el sistema. Esto se debe a que el sistema es considerado balanceado, ya que está conectado a cargas lineales que no generan distorsión armónica. En la Fig. 4, se pueden visualizar las ondas fasoriales sin distorsión.
Etapa 3: Sistema equilibrado con una carga no lineal
Con los datos del circuito de prueba de la Fig. 6, se evalúa la condición de introducción de la carga no lineal en la red y se verifican las distorsiones que se propagan por todo el sistema. En el circuito de distribución trifásico mostrado en la Fig. 5, se incorporó una carga no lineal trifásica proveniente de un dispositivo electrónico de potencia, compuesto por una resistencia de 100 (ohms) y una inductancia de 10e-3 mH, en la barra 3. Esta carga no lineal afecta a todo el sistema de distribución trifásica.
En la Tabla 2, cada fila representa una barra en la red eléctrica, y las columnas corresponden a diferentes armónicos de frecuencia del voltaje. Los valores en la tabla indican el porcentaje de la amplitud de cada armónico con respecto al voltaje fundamental, expresado como un porcentaje (V%).
Tabla 2: Índice de porcentaje alto de armónica a nivel de Voltaje con la instalación de una carga no lineal.
| Bus | Armónico de frecuencia de Voltaje (V%) | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 7 | 11 | 13 | 17 | |
| 1 | 100 | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 |
| 2 | 100 | 1.60 | 1.09 | 1.26 | 0.99 | 1.03 |
| 3 | 100 | 1.73 | 1.18 | 1.37 | 1.07 | 1.12 |
En la Tabla 3 se presentan los altos porcentajes de armónicos en nivel de corriente en diferentes barras después de la instalación de una carga no lineal. Los valores indican el porcentaje de la amplitud de cada armónico con respecto a la corriente fundamental, expresado como un porcentaje (I%).
Tabla 3: Índice de porcentaje alto de armónica a nivel de Corriente con la instalación de una carga no lineal.
| Bus | Armónico de frecuencia de Corriente (I%) | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 7 | 11 | 13 | 17 | |
| 1 | 100 | 3.49 | 1.64 | 1.28 | 0.83 | 0.70 |
| 2 | 100 | 3.50 | 1.64 | 1.38 | 0.83 | 0.70 |
| 3 | 100 | 10.82 | 5.08 | 3.99 | 2.60 | 2.15 |
En la Tabla 4 se presenta el Índice de Distorsión Armónica Total (THD) de voltaje y corriente en diferentes barras después de la instalación de una carga no lineal. Este índice indica el alto porcentaje de armónicos presentes en todos los sistemas de distribución trifásicos y su progresiva afectación en toda la red.
Tabla 4: Índice de Armónica Total de Voltaje y Corriente presente con la instalación de una carga no lineal
| Bus | THDv % | THDi % |
| 1 | 0.17 | 4.29 |
| 2 | 3.35 | 4.30 |
| 3 | 3.63 | 13.30 |
Como resultado de la introducción de la carga no lineal en el sistema de distribución trifásico, la Fig. 6 muestra los resultados de voltaje y corriente con una alta tasa de distorsión armónica, como se puede observar en las tres fases trifásicas.
Sincronización del filtro pasivo
En el diseño del filtro pasivo el objetivo fundamental es el desarrollo del proceso general para las tres fases que se integran al sistema trifásico con parámetros de R, L y C para el filtro selecciona aplicando ecuaciones descritas a continuación[13]:
En la impedancia para la frecuencia fundamental se calcula de acuerdo a la ecuación (1).
La reactancia efectiva para cada fase se calcula mediante la ecuación (2).
Por lo tanto, la reactancia capacitiva se calcula para cada fase con la ecuación (3).
La capacitancia se calcula mediante la ecuación (4) para cada fase.
De esta manera se calcula en la ecuación (5) la reactancia inductiva para cada fase.
Mientras que la inductancia se calcula mediante la ecuación (6) en cada fase.
Y la resistencia se calculó para cada fase mediante la ecuación (7).
Etapa 2: Teoría de la Optimización no lineal
La presente investigación se lleva a cabo mediante un conjunto secuencial de actividades que exploran temas relevantes desde una perspectiva teórica y documental. Se emplea la teoría de la optimización no lineal para determinar los valores óptimos de las variables de decisión en un problema específico. En otras palabras, se busca encontrar tanto el máximo como el mínimo de una función dada, sujetos a restricciones y limitaciones establecidas por el problema en cuestión. Este estudio aborda varios escenarios detallados, como se puede observar en la Fig. 7, donde se presenta la metodología aplicada al problema de los armónicos en la red eléctrica.
Esta etapa considera los elementos esenciales necesarios para el análisis del modelado utilizando la teoría de la optimización. Además, define elementos adicionales que no están cubiertos por este análisis pero que son significativos. La función principal del estudio se basa en la ecuación (8), que representa las pérdidas cuadráticas presentes en todo el sistema trifásico. Esto incluye los conductores del circuito primario y secundario, así como el núcleo de los transformadores de distribución, junto con el impacto de las cargas no lineales en el sistema. Las restricciones del sistema incluyen la compensación de la potencia reactiva y la minimización de los armónicos presentes en el sistema de distribución, hasta igualarlos a cero [14][15].
Minimizar:
Sujeto a:
Donde:
Para realizar la minimización de la corriente de línea y la corriente de compensación, se multiplica el voltaje y la corriente por un porcentaje de error, lo cual puede expresarse mediante una ecuación (10) [14].
Para obtener las condiciones estacionarias y de factibilidad utilizando el método de Karush-Kuhn-Tucker (KKT), se deriva la ecuación relevante a la corriente del filtro (∂iqk), y la variación del error considerado (∂λ).
Supongamos que la ecuación (10) se define como:
Una vez completado la multiplicación, se obtiene la tensión de línea (vk) de acuerdo con la ecuación (11), la cual simplifica la potencia activa del filtro.
Para realizar esto, se debe eliminar la corriente del filtro que afecta las tres fases de voltaje y corriente del circuito de prueba, utilizando la ecuación (12).
Para calcular la potencia trifásica considerando los errores presentes en el circuito, se utiliza la ecuación (13).
Con esto se busca determinar el valor óptimo de lambda optimo (λ) mediante la ecuación (14), como parte del proceso de control para activar el filtro activo en las tres fases que se incorporan al sistema.
Reemplazando en la ecuación (15) descrita.
Es posible obtener la ecuación (16) de control necesaria para programar el filtro de potencia activo en el sistema eléctrico ajustando iqk para compensar y mitigar armónicos o mejorar la calidad de la energía.
ANALISIS DE RESULTADOS
En esta etapa, se considera el uso del filtrado pasivo tradicional y se explora otro método para reducir la distorsión armónica en la red eléctrica causada por cargas no lineales. Los filtros se implementan en la red de distribución eléctrica mostrada en la Fig. 8 para regular y mitigar los efectos de los armónicos y las perturbaciones en la red. Factores como la cantidad de armónicos presentes, el nivel de distorsión, la capacidad de corriente y el voltaje nominal necesario son determinantes en el dimensionamiento del filtro pasivo. [16][17].
El análisis utiliza una conexión en paralelo para un filtro pasivo que consta de tres fases:
Fase A: RLC en serie con un condensador de 8.02 μF, una inductancia de 35.8 mH y una resistencia de 3.34 ohmios.
Fase B: RLC en serie con un condensador de 4.02 μF, una inductancia de 36.13 mH y una resistencia de 1.173 ohmios.
Fase C: RLC en serie con un condensador de 4.14 μF, una inductancia de 14.56 mH y una resistencia de 1.48 ohmios.
Estos componentes están diseñados para mitigar la distorsión armónica y otros efectos no deseados en la red eléctrica, especialmente en presencia de cargas no lineales. Para asegurar un suministro de energía más limpio y confiable, estos filtros se colocan estratégicamente en toda la red eléctrica para eliminar o atenuar las frecuencias no deseadas.
En la Tabla 5 se presentan los altos índices de armónicos a nivel de voltaje después de aplicar un filtro pasivo. Los valores en esta tabla indican el porcentaje de la amplitud de cada armónico con respecto al voltaje fundamental, expresado en porcentaje (V%).
Tabla 5: Índice de porcentaje alto de armónico a nivel de Voltaje mediante el filtro pasivo.
| Bus | Armónico de frecuencia de Voltaje (V%) | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 7 | 11 | 13 | 17 | |
| 1 | 100 | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 |
| 2 | 100 | 0.95 | 1.03 | 0.51 | 0.68 | 0.82 |
| 3 | 100 | 1.03 | 1.12 | 0.56 | 0.74 | 0.89 |
En la Tabla 6 se presentan los altos índices de armónicos a nivel de corriente después de aplicar un filtro pasivo. Los valores en esta tabla indican el porcentaje de la amplitud de cada armónico con respecto a la corriente fundamental, expresado en porcentaje (I%).
Tabla 6: Índice de porcentaje alto de armónico a nivel de Corriente mediante el filtro pasivo.
| Bus | Armónico de frecuencia de Corriente (I%) | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 7 | 11 | 13 | 17 | |
| 1 | 100 | 1.29 | 1.03 | 0.28 | 0.36 | 0.36 |
| 2 | 100 | 1.30 | 1.03 | 0.29 | 0.36 | 0.36 |
| 3 | 100 | 2.45 | 1.96 | 0.55 | 0.70 | 0.68 |
En la Tabla 7 se presenta el Índice de Distorsión Armónica Total (THD) de voltaje y corriente después de aplicar un filtro pasivo, considerando la mínima distorsión armónica total en el voltaje y la corriente.
Tabla 7: Índice de Armónico Total de Voltaje y Corriente mediante el filtro pasivo.
| Bus | THDv % | THDi % |
| 1 | 0.17 | 1.82 |
| 2 | 2.52 | 1.83 |
| 3 | 2.74 | 3.45 |
El filtro pasivo mostrado en la Fig. 9 permite verificar la onda sinusoidal de voltaje y corriente, además de reducir los armónicos de onda a un nivel beneficioso para la calidad de energía del sistema de distribución [18].
Basándonos en los datos de la Tabla 4, la introducción de una carga no lineal en la red eléctrica resulta en un alto nivel de distorsión armónica. Este escenario se confirma en un circuito de prueba mostrado en la Fig. 10, donde la carga no lineal afecta todo el sistema. Las formas de onda de voltaje y corriente en cada nodo del circuito de prueba muestran claramente los efectos de la distorsión armónica.
Para abordar este problema, estamos examinando la teoría de la optimización del filtro. Esta teoría nos permite mejorar el rendimiento general del sistema al mejorar la calidad de la energía, especialmente al reducir los efectos de la distorsión armónica causada por cargas no lineales.
La ecuación de control (16), que se deriva de la aplicación teórica de señales de forma de onda de corriente y voltaje distorsionadas causadas por la inyección de carga no lineal, utiliza las ecuaciones del estudio de optimización no lineal. La lógica de control procesa la señal de error en una banda de histéresis (HB), donde la condición activa se establece en -0.5 y se desactiva en 0.5. Esta banda de histéresis regula el filtrado de corriente activa, permitiendo el control de las señales de salida trifásicas.
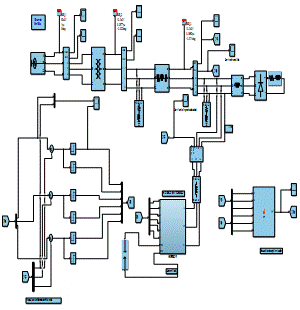
Figura 10: Circuito del caso base de distribución trifásica tipo radial con la Teoría de Optimización no lineal.
La forma de onda generada se introducirá en un inversor, que utilizará condensadores (100 ^ 3 ohmios) para almacenar energía para su funcionamiento. Se utilizarán seis IGBTs, con resistencias internas (10 ^-3 ohmios) y dos resistencias adicionales de (100 ohmios) (0, 1^-06 faradios), para modelar estos elementos Esto permite equilibrar la corriente de salida mediante pulsos para compensar la no linealidad y la falta de ondulación de las cargas.
En este análisis se obtuvieron datos reales del circuito de caso base, donde se registraron niveles estables de distorsión armónica en el circuito [19].
En la Tabla 8 se presenta el Índice de Armónicos de Voltaje con la carga no lineal utilizando la Teoría de Optimización No Lineal. Los valores en la tabla representan el porcentaje de la amplitud de cada armónico con respecto al voltaje fundamental, expresado en porcentaje (V%). Se observa que los valores de los armónicos de frecuencia de voltaje son muy bajos en todas las barras, lo que indica una mínima distorsión armónica en el voltaje después de aplicar la Teoría de Optimización No Lineal. Esto sugiere una reducción significativa en la distorsión armónica del voltaje en las barras 1, 2 y 3 después de implementar esta teoría.
Según los resultados presentados en la tabla 9, se muestra el índice armónico de la corriente con carga no lineal utilizando la teoría de optimización no lineal. Los valores de los armónicos de frecuencia de la corriente son muy bajos en todas las barras, lo que indica una mínima distorsión armónica en la corriente después de aplicar la Teoría de Optimización No Lineal. De manera similar, en las barras 1, 2 y 3, los valores de los armónicos de frecuencia de la corriente también son muy bajos, lo cual señala una reducción significativa en la distorsión armónica de la corriente después de aplicar esta teoría.
Tabla 8: Índice de Armónico de Voltaje con la carga no lineal mediante la Teoría de Optimización No Lineal.
| Bus | Armónico de frecuencia de Voltaje (V%) | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 7 | 11 | 13 | 17 | |
| 1 | 100 | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 |
| 2 | 100 | 0.17 | 0.10 | 0.13 | 0.12 | 0.13 |
| 3 | 100 | 0.26 | 0.18 | 0.22 | 0.20 | 0.21 |
Tabla 9: Índice de Armónico de Corriente con la carga no lineal mediante la Teoría de Optimización No Lineal.
| Bus | Armónico de frecuencia de Corriente (I%) | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 7 | 11 | 13 | 17 | |
| 1 | 100 | 0.14 | 0.10 | 0.07 | 0.06 | 0.04 |
| 2 | 100 | 0.14 | 0.10 | 0.07 | 0.06 | 0.04 |
| 3 | 100 | 11.19 | 5.59 | 4.41 | 3.13 | 2.18 |
La Tabla 10 muestra los resultados de este estudio en comparación con los reportados en la literatura, donde se evidencia que la aplicación del filtro utilizando la teoría de optimización ha sido exitosa en la reducción de la distorsión armónica tanto en el voltaje como en la corriente de la red eléctrica. Los valores tan bajos de THD indican una mejora significativa en la calidad del suministro eléctrico, lo cual puede prevenir problemas asociados con la distorsión armónica y asegurar un funcionamiento más eficiente y confiable del sistema eléctrico.
Tabla 10: Utilizando la teoría de optimización, el filtro se conecta a los índices de distorsión armónico 𝑻??𝑫 𝒗 y 𝑻𝑯𝑫 𝒊 con una carga no lineal.
| Bus | THDv % | THDi % |
| 1 | 0.17 | 0.57 |
| 2 | 0.54 | 0.57 |
| 3 | 0.86 | 0.57 |
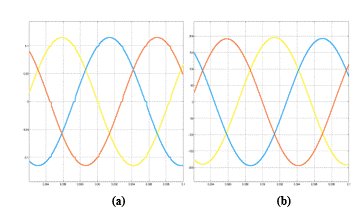
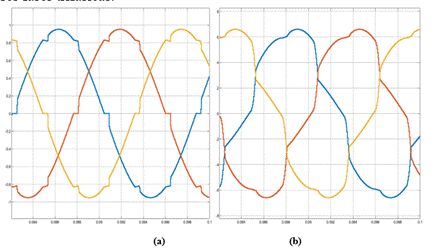
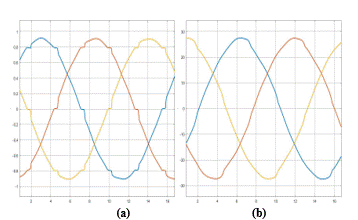
Figura 11: Las ondas armónicas conectado el filtro activo con la teoría de optimización: (a) Voltaje; (b) Corriente
Basado en los resultados presentados en la Tabla 8, Tabla 9 y Tabla 10, al introducir el filtro con la teoría de optimización en el sistema de prueba, se confirma que los armónicos en el voltaje y la corriente se han minimizado considerablemente a un nivel favorable para la calidad de energía del sistema de distribución, como se muestra en la Fig. 11. Además, el filtro con optimización no lineal está diseñado para compensar la potencia reactiva y reducir la presencia de armónicos a un nivel aceptable, lo que permite que el sistema continúe entregando energía con un menor índice de armónicos.[20].
DISCUSIÓN
En este estudio, se realizó un análisis de armónicos comparando el método tradicional del filtro pasivo con la nueva tendencia de aplicar la teoría de optimización al filtro activo. Se compararon los porcentajes de reducción de armónicos de voltaje y corriente en un sistema trifásico después de la introducción de una carga no lineal.
Tabla 11: Comparación de los dos filtros aplicados en el caso base de 3 barras.
| BARRAS | Filtro Pasivo | Filtro Activo de potencia | % entre los métodos | Filtro Pasivo | Filtro Activo de potencia | % entre los métodos | THDv % THDv % THDi % THDi %
| 1 | 0.17 | 0.17 | 0 | 1.82 | 0.57 | 1.25 |
| 2 | 2.52 | 0.54 | 1.98 | 1.83 | 0.57 | 1.26 |
| 3 | 2.74 | 0.86 | 1.88 | 3.45 | 0.57 | 2.88 |
Basándose en los resultados recopilados en cada etapa, donde se introdujeron filtros para mejorar la calidad de la energía eléctrica frente a la distorsión armónica de voltaje y corriente provocada por la carga no lineal, se pudo experimentar su impacto en todo el sistema. La Tabla 11 muestra una comparación notable del filtro más eficaz que logra reducir mínimamente el porcentaje de distorsión armónica en todo el sistema. De esta manera, se confirma la eficacia del filtro activo de potencia, ya que logra un nivel de reducción más aceptable en los THDv (distorsión armónica total de voltaje) y THDi (distorsión armónica total de corriente) en el caso base.
Es importante destacar que el filtro de optimización no lineal ha sido desarrollado en los últimos años con el objetivo específico de reducir los THDv y THDi. La programación de este filtro es especialmente útil para investigaciones a gran escala y contribuye significativamente al progreso tecnológico en el campo de la calidad de energía eléctrica. Este filtro utiliza estándares y análisis avanzados que demuestran su superioridad sobre otros métodos convencionales, ofreciendo un alto porcentaje de compensación de potencia reactiva cuando se implementa en sistemas de energía trifásica.
En la Tabla 12 se realiza una comparación de las características de ambos filtros, según revisiones técnicas y metodológicas, para su diseño y aplicación.
Se compararon ambos tipos de filtros para determinar cuál era el más adecuado según los resultados obtenidos en el estudio. En la Tabla 12 se detallan las características relevantes que llevaron a seleccionar el filtro activo de potencia. Este filtro fue elegido por su alta eficiencia en la reducción de armónicos de voltaje y corriente, así como por la capacidad de control que ofrece mediante la teoría de optimización y la programación de condiciones específicas.
Tabla 12: Comparación técnica para seleccionar el filtro.
| CARACTERÍSTICA | FILTRO PASIVO | FILTRO ACTIVO DE POTENCIA |
| Costo de implantación | Bajo | Alto |
| Compensación de energía reactiva de carácter inductivo. | Bajo | Alto |
| Reducción de armónicos. | Bajo | Alto |
| Componentes de los filtros. | Bajo | Alto |
| Algoritmo de control apropiados. | Ninguno | Alto |
| Topología de los filtros de potencia. | Bajo | Alto |
| Cálculo del diseño de filtro. | Bajo | Alto |
| Control del Filtro. | Bajo | Alto |
| Avance Tecnológico. | Bajo | Alto |
| Estructura del filtro. | Bajo | Alto |
| Mantenimiento del dispositivo. | Medio | Bajo |
| Ahorro en facturación. | Bajo | Alto |
| Diseño de la estructura del dispositivo. | Bajo | Alto |
| Los componentes del filtro son voluminosos, pesados. | Alto | Bajo |
| La ganancia en potencia y la sintonización del dispositivo con la red. | Alto | Bajo |
| Sensibilidad. | Baja | Alto |
| Señales de salida. | Bajo | Alto |
| Impedancia. | Alto | Bajo |
| Alimentación. | Ninguno | Alto |
CONCLUSIONES
Controlar las activaciones del filtro y reducir los armónicos en sistemas con cargas no lineales requiere una comprensión profunda de las condiciones de Karush-Kuhn-Tucker (KKT). Estas condiciones proporcionan un marco robusto para encontrar soluciones óptimas.
La implementación de filtros pasivos adecuados puede reducir significativamente los efectos de armónicos y perturbaciones presentes en el circuito de caso base. Esto puede resultar en una reducción mínima del 80% en la distorsión armónica de voltaje y corriente, lo que contribuye a una mayor estabilidad del sistema. En comparación, los filtros activos de potencia pueden lograr una reducción mínima del 90% en la distorsión armónica de voltaje y corriente mediante un control más preciso, lo que los hace más efectivos en la minimización de armónicos y, por ende, más aceptados en aplicaciones donde se requiere una reducción más drástica de la distorsión armónica.
La teoría de optimización no lineal, aplicada al modelado de filtros de potencia activos, puede efectivamente reducir los armónicos tanto en el voltaje como en la corriente del sistema. Este enfoque permite un control preciso del filtro activo, mejorando así la calidad de la energía eléctrica al mitigar la distorsión armónica. Además, este tipo de filtro puede integrarse eficazmente en sistemas que utilizan fuentes de energía renovables intermitentes, como la energía solar y eólica. Esto ayuda a abordar los desafíos asociados con la variabilidad inherente de estas fuentes, contribuyendo a la estabilidad y fiabilidad del sistema eléctrico global.