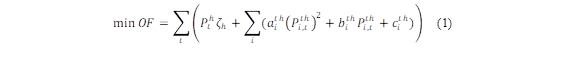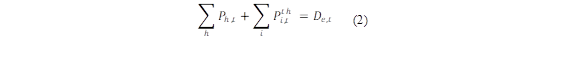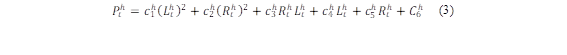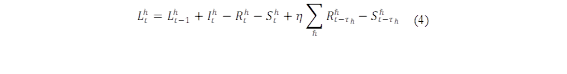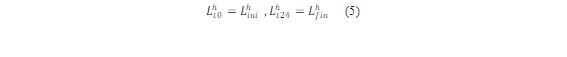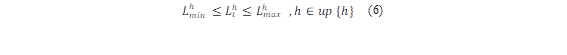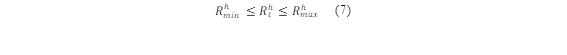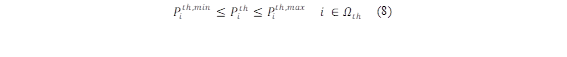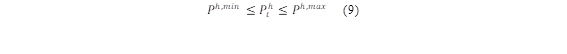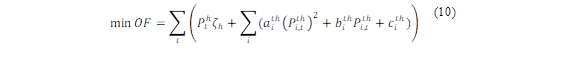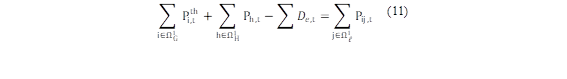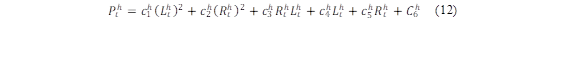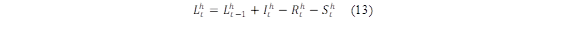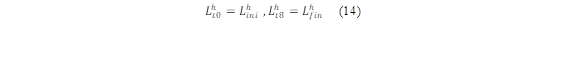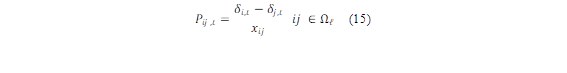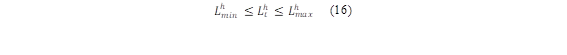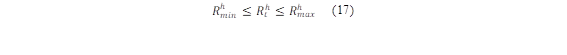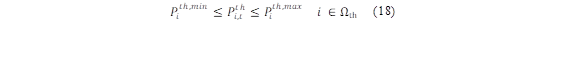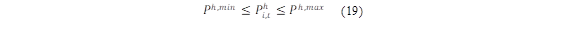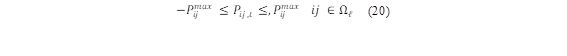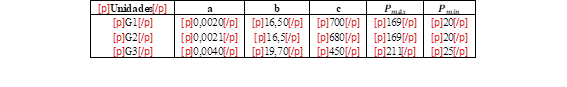INTRODUCCIÓN
El parque generador del Sistema Eléctrico Ecuatoriano está compuesto por diferentes tipos de centrales, como hidroeléctricas, termoeléctricas y de energía renovable. Las centrales hidroeléctricas y termoeléctricas son las principales fuentes de generación de energía eléctrica en el país. Para controlar la operación y el despacho económico de estas centrales, se utiliza un modelo de optimización hidrotérmica. Este modelo permite determinar la mejor utilización de los recursos energéticos disponibles y tener en cuenta las restricciones que se presentan, con el objetivo de minimizar los costos operativos del parque generador.
El despacho económico es un área de investigación activa en la operación de los sistemas de potencia, ya que implica analizar múltiples perspectivas y controlar diversos parámetros debido a las características dinámicas del sistema. La programación de la generación busca resolver los problemas de operación al coordinar la operación del sistema eléctrico, considerando aspectos técnicos, operativos y económicos para garantizar la confiabilidad, seguridad y suministro de energía, al mismo tiempo que se maximizan los beneficios y se minimizan los costos asociados a la generación. Existen diferentes métodos de optimización, tanto clásicos como heurísticos, que se aplican según las necesidades y características de cada región y el modelo de su matriz energética. Sin embargo, la información sobre estos métodos está dispersa, lo que dificulta una comprensión más profunda y la correcta aplicación teniendo en cuenta los diferentes parámetros a controlar en el despacho económico.
En consecuencia, existen varias investigaciones sobre el problema de despacho económico en las cuales se plantean diferentes metodologías como [1] que muestra el despacho de las unidades térmicas presentes en un sistema hidrotérmico por medio del uso del algoritmo de optimización que utiliza la inteligencia de las luciérnagas y sugiere ampliar el estudio del mismo considerando las restricciones totales del sistema. Usando otro método heurístico [2] aborda una metodología que incorpora restricciones de estabilidad transitoria utilizando Particle Swarm Optimization (PSO) para integrar todos los elementos considerados en el modelo, este logra una rápida convergencia y soluciones de buena calidad.
En efecto los modelos heurísticos utilizados para resolver los problemas de optimización mediante aproximación intuitiva se califica como un procedimiento para el que se tiene un alto grado de confianza en que encuentra soluciones de alta calidad con un coste computacional razonable, aunque no se garantice su optimalidad o su factibilidad [3], además que se usa el calificativo heurístico en contraposición a exacto.
Dicho lo anterior, mediante la programación no lineal dado a que no trabaja con aproximaciones, sino que se rige a la formulación matemática que se encuentra contemplada y está obligada a seguir todos los límites y restricciones que se le han implantado con el fin de minimizar el costo de operación del despacho económico horario. Dando como resultado el cómo comprender de forma sintetizada y analítica el modelamiento de los sistemas eléctricos con sus parámetros y variables respectivamente. Por ende se realizan investigaciones como [4] presentan una aplicación computacional para llevar a cabo el despacho económico en un sistema de energía eléctrica utilizando MATLAB utilizando la técnica de los multiplicadores de Lagrange en el cual puede mostrar el proceso y los resultados de una manera didáctica.
De igual manera entorno a la programación clásica se han desarrollado modelos como en [5] y [6] que muestran resultados satisfactorios en cuanto a la entrega de potencia para cubrir la demanda cumpliendo con las restricciones impuestas. Dicho esto, con respecto a la programación no lineal existen varios modelos los cuales describen sistemas uninodales los cuales son modelos incompletos ya que los sistemas eléctricos están asociados directamente entre si mediante las líneas de transmisión, es por eso que en este documento se ha desarrollado en primera instancia el modelo de un solo nodo para posteriormente realizar el despacho económico implementado al modelo de la IEEE de 14 nodos.
Dado a que ya se ha planteado anteriormente sobre que metodología es más eficiente dentro de los problemas de optimización, prueba de ello es la investigación realizada en [7] que establece una comparación entre los métodos clásicos y metaheurísticos de optimización, al intentar optimizar la planificación del movimiento de un robot, se llegó a la conclusión que en esta situación en los métodos metaheurísticos daban como resultado un rendimiento superior, sin embargo en la segunda etapa hicieron la comparación para optimizar la configuración de sistemas de generación distribuida y concluyeron que los métodos clásicos lograron una mejor solución para minimizar las pérdidas de potencia que los métodos metaheurísticos.
Por otro lado, en el ámbito de planificación considerando los factores externos, [8] menciona ventajas de los métodos metaheurísticos sobre los clásicos, una ventaja importante es que logra conducir a soluciones suficientemente buenas para los problemas no lineales, es decir, problemas para los cuales no existe ningún algoritmo exacto conocido que pueda resolverlos en un tiempo razonable, además hace énfasis en que logra resolver problemas con gran complejidad de entradas, lo que presentaría un problema para los métodos clásicos. Teniendo en cuenta lo mencionado anteriormente, debido a que no se considera factores externos, ni incertidumbres en las variables, la programación no lineal representa una buena herramienta para resolver los problemas de despacho económico.
Dicho esto, el progreso de las investigaciones en la optimización de la entrega de energía, ya sea a través de modelos clásicos o metaheurísticos, muestra un avance significativo en el aporte a la ciencia. Es fundamental resolver estos problemas en el menor tiempo posible, por lo tanto, el enfoque futuro se centra en desarrollar y proponer modelos o metodologías que permitan encontrar soluciones óptimas utilizando la menor cantidad de recursos del procesador. Si bien el uso de modelos de prueba nos permite desarrollar dichas metodologías con la finalidad de resolver de manera eficiente los problemas optimización, esta investigación propone dos modelos los cuales serán resueltos mediante programación no lineal que permitirá a futuro que se deriven problemas más complejos a partir de estos.
MODELO HIDROTÉRMICO DE UN NODO CON EMBALSES EN CASCADA
Sujeto a:
Características del sistema
Tabla 1: Demandas del sistema de uno nodo para un periodo de 24 horas [9]
| Demanda (MW) | |||||
|---|---|---|---|---|---|
| Hora | PD | Hora | PD | Hora | PD |
| 1 | 1370 | 9 | 2240 | 17 | 2130 |
| 2 | 1390 | 10 | 2320 | 18 | 2140 |
| 3 | 1360 | 11 | 2230 | 19 | 2240 |
| 4 | 1290 | 12 | 2310 | 20 | 2280 |
| 5 | 1290 | 13 | 2230 | 21 | 2240 |
| 6 | 1410 | 14 | 2200 | 22 | 2120 |
| 7 | 1650 | 15 | 2130 | 23 | 1858 |
| 8 | 2000 | 16 | 2070 | 24 | 1590 |
Tabla 2: Coeficientes de potencia de generación hidráulica [9]
| Unidades | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| 1 | -0,0042 | -0,42 | 0,03 | 0,9 | 10 | -50 |
| 2 | -0,004 | -0,3 | 0,015 | 1,14 | 9,5 | -70 |
| 3 | -0,0016 | -0,3 | 0,014 | 0,55 | 5,5 | -40 |
| 4 | -0,003 | -0,31 | 0,027 | 1,44 | 14 | -90 |
Tabla 4: Límites de capacidad de almacenaje, límites de descarga y límites de generación hidráulica [9]
| Planta | V 𝐦𝐢𝐧 𝑽 𝒎á𝒙 𝑽 𝒊𝒏𝒊 𝑽 𝒇𝒊𝒏 𝑸 𝒎𝒊𝒏 𝑸 𝒎á𝒙 𝑷 𝒉 𝒎𝒊𝒏 𝑷 𝒉 𝒎á𝒙 x10 4 [ m 3 ]MW | MW | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 80 | 150 | 100 | 120 | 5 | 15 | 0 | 500 |
| 2 | 60 | 120 | 80 | 70 | 6 | 15 | 0 | 500 |
| 3 | 100 | 240 | 170 | 170 | 10 | 30 | 0 | 500 |
| 4 | 70 | 160 | 120 | 140 | 13 | 25 | 0 | 500 |
Los coeficientes de la función de costo de cada unidad térmica (unidad monetaria $/MW) y los límites de potencia de generación se especifican en la Tabla 5.
MODELO DE DESPACHO HIDROTÉRMICO CON LÍNEAS DE TRANSMISIÓN
Considerando los modelos planteados anteriormente se formula un nuevo modelo no lineal para la coordinación hidrotérmica de la siguiente manera:
Sujeto a:
Características del sistema
Tabla 6: Coeficientes de potencia de generación hidráulica [9]
| Unidades | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| H1 | -0,0042 | -0,42 | 0,03 | 0,9 | 10 | -50 |
| H2 | -0,004 | -0,3 | 0,015 | 1,14 | 9,5 | -70 |
Tabla 7: Límites de capacidad de almacenaje, límites de descarga y límites de generación hidráulica [9]
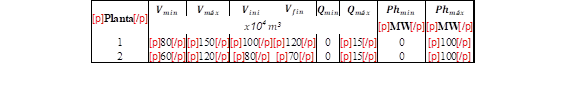
Para este modelo se tomará la misma tabla de entrada de agua de la mostrado en la Tabla 3.
| LINEAS | Reactancia (p.u) | Límite de transmisión [MW] |
|---|---|---|
| 1-2 | 0,0592 | 200 |
| 1-5 | 0,223 | 200 |
| 2-4 | 0,1763 | 200 |
| 2-3 | 0,0198 | 200 |
| 2-5 | 0,1739 | 200 |
| 3-4 | 0,171 | 200 |
| 4-5 | 0,0421 | 200 |
| 4-7 | 0,2091 | 200 |
| 4-9 | 0,5562 | 200 |
| 5-6 | 0,252 | 200 |
| 6-11 | 0,1989 | 200 |
| 6-12 | 0,2558 | 200 |
| 6-13 | 0,1303 | 200 |
| 7-8 | 0,1762 | 200 |
| 7-9 | 0,11 | 200 |
| 9-10 | 0,0845 | 200 |
| 9-14 | 0,2704 | 200 |
| 10-11 | 0,1921 | 200 |
| 12-13 | 0,1999 | 200 |
| 13-14 | 0.348 | 200 |
Debido a la gran cantidad de datos que representa la demanda para el sistema de la IEEE de 14 barras, se tomaron los datos de demanda de [11] para un periodo de 24 horas, considerando que esta demanda está pronosticada para un día típico de invierno.
Donde: i,j Índice de los nodos de la red t Intervalos de tiempo h Índice de unidades de generación hidráulica th Índice de unidades de generación térmica Ω_H^i Conjunto de todas las unidades de generación hidráulica conectadas al nodo i. Ω_G^i Conjunto de todas las unidades de generación térmica conectadas al nodo i. Ω_l^i Conjunto de todas las líneas conectadas al nodo i a_i^th,b_i^th,c_i^th Coeficientes de costo de combustible de la unidad térmica i D_(e,i) Demanda de potencia activa en el nodo i P_i^(th,max /min) Límites máximo y mínimo de generación de potencia activa de la unidad térmica i en (MW). P_i^(h,max /min) Límites máximo y mínimo de generación de potencia activa de la unidad hidráulica i en (MW). R_t^h Agua liberada por el embalse en el tiempo t R_(max/min)^h Límite máximo y mínimo de agua liberada por el embalse I_t^h Los influjos o entradas de agua en el tiempo t L_t^h Volumen del embalse en el tiempo t L_(max/min)^h Limites máximo y mínimo de volumen del embalse en el tiempo t P_ij^max Límite máximo de flujo de energía que conecta el nodo i al j x_ij Reactancia que conecta el nodo i al j P_i^th Potencia activa generada por unidad térmica i P_i^h Potencia activa generada por unidad hidráulica i P_i^h Potencia activa generada por unidad hidráulica i P_ij Flujo de potencia que conecta el nodo i al j . δ_i Angulo en el nodo i OF Costo total de Operación ($)
FORMULACIÓN DEL PROBLEMA
La función objetivo está representada en (1) y (10). El objetivo es encontrar el despacho de potencia térmica e hidráulica de tal manera que se minimiza el costo total de operación [12]. Esta función se encuentra bajo ciertos parámetros y restricciones que debe cumplir.
Restricciones operativas de los sistemas
Los modelos deberán tienen las siguientes restricciones:
Características de generación de potencia térmica e hidráulica
Las unidades térmicas están formadas generalmente por calderas que permiten que se cumpla el ciclo de generación, por tanto estas unidades se encuentran asociadas a características de entrada-salida expresada en términos de combustible (USD/h) estas son mostradas en la ecuaciones (1) y (10) en donde de denominan coeficientes a,b,c [13]. Mientras tanto, en una central hidroeléctrica, las turbinas transforman la energía potencial del agua en energía cinética, la cual se convierte en electricidad mediante los generadores. Este tipo de generación ha tenido un papel significativo en el funcionamiento seguro, estable y eficiente de los sistemas eléctricos y está representado por la ecuaciones (3) y (12) asociada con sus coeficientes de turbinado c1-c6 que dependerán de las características propias de cada unidad [14], Sabiendo que la centrales hidráulicas no tienen un costo de combustible como tal se debe asumir un costo variable, este será considerado en 14 $/MW siguiendo la metodología de [15].
Balance de potencia
Así es como la restricción de balance de potencia donde se plantea que la suma de la generación de energía de las unidades individuales sea igual a la demanda total de energía como se muestra en las ecuaciones (2) y (11) [16].
Límites de generación térmica e hidráulica
Las unidades de generación tanto térmica como hidráulica deben establecer límites máximos y mínimos, los cuales deben respetarse para la correcta operación de la máquina, estas estas dependerán netamente de las características técnicas de la máquina las cuales se muestran en las ecuaciones (8),(9),(18) y (19).
Volumen de embalses
Cuando una cuenca de río tiene un gran potencial hidrológico, es común construir centrales hidroeléctricas en cascada para aprovechar múltiples veces la energía del agua [17]. Esto implica tener en cuenta la entrada de agua, niveles máximos y mínimos que se deben respetar para que el embalse cumpla con su función, esto mostrado en las ecuaciones (4-(7),(13-(14) y (16(17).
Límites de transmisión de potencia
El límite térmico de un conductor para líneas aéreas es la corriente máxima permitida, considerando una temperatura máxima a través del conductor para condiciones ambientales establecidas [18], por lo tanto estas están restringidas a cierto nivel de potencia que garantiza el correcto funcionamiento de los conductores, estos límites están representados por la ecuación (20).
PROPUESTA DE SOLUCIÓN MEDIANTE PROGRAMACIÓN NO LINEAL
A continuación, se presenta una propuesta de solución para abordar el problema del despacho hidrotérmico utilizando técnicas de programación no lineal y su implementación en el software GAMS. El despacho hidrotérmico es un desafío importante en la gestión eficiente de sistemas eléctricos, ya que implica la optimización de la generación de energía a partir de fuentes hidroeléctricas y térmicas, teniendo en cuenta la disponibilidad de recursos y las restricciones operativas.
La programación no lineal se presenta como una herramienta poderosa para abordar este problema complejo, ya que permite modelar las variables y las restricciones que intervienen en el despacho hidrotérmico de manera más precisa y realista. En este sentido, el software GAMS se convierte en una excelente opción para implementar y resolver estos modelos de programación no lineal[19], ya que a través de su licencia comunitaria permite modelar y resolver problemas lineales (LP, RMIP y MIP) que no superan las 5000 variables y 5000 restricciones. Para todos los demás tipos de modelos como (PNL), el modelo no puede tener más de 2500 variables y 2500 restricciones. La propuesta se basa en la formulación de un modelo matemático no lineal que representa el despacho hidrotérmico y su implementación en el software GAMS para encontrar la solución óptima. En el modelo, se consideran variables como la generación hidroeléctrica y térmica, la demanda eléctrica, la capacidad de almacenamiento de los embalses y las restricciones operativas.
El software GAMS brinda una interface flexible y eficiente para implementar y resolver modelos de programación no lineal. Su lenguaje de modelado nos permite describir el problema del despacho hidrotérmico de manera clara y concisa, definiendo las variables, las restricciones y la función objetivo. Además, GAMS ofrece una amplia variedad de algoritmos de optimización no lineal que nos permiten encontrar soluciones óptimas de manera eficiente.
En resumen, nuestra propuesta de solución del despacho hidrotérmico mediante programación no lineal se apoya en el uso del software GAMS como una herramienta integral para la implementación y resolución de modelos. A través de esta combinación, buscamos mejorar la eficiencia y la sostenibilidad de los sistemas eléctricos al considerar de manera más precisa las características y las limitaciones de las fuentes de generación hidroeléctrica y térmica.
Para validar y evaluar la propuesta se tomó como referencia el problema planteado en [7] en donde se analizaron los resultados en base a los parámetros establecidos que fue la base para el desarrollo del modelo de varios nodos.
En sí, la integración de la programación no lineal y el software GAMS en la propuesta de solución del despacho hidrotérmico nos brinda una metodología robusta y eficiente para abordar este desafío energético, se espera que esta investigación contribuya al avance en la gestión óptima de la generación de energía eléctrica y promueva la sostenibilidad en los sistemas eléctricos.
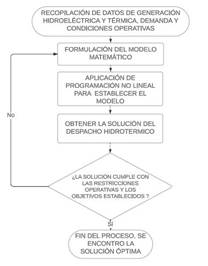
En primera instancia se realiza la recopilación de datos de generación tanto térmica como hidroeléctrica mediante la revisión del estado del arte para su posteriormente realizar la formulación matemática que comprenderá en la composición de las variables y parámetros técnicos encontrados en la investigación, luego esa formulación es plasmada mediante programación no lineal al software de optimización GAMS, una vez obtenido los resultados, se analiza si el despacho cumple con las restricciones operativas y objetivos establecidos, si cumple se habrá encontrado la solución óptima, sino se tendrá que revisar la formulación matemática.
ANÁLISIS DE RESULTADOS
Una vez realizada la programación de los modelos matemáticos presentados en las secciones anteriores, y con ayuda de las técnicas de optimización con restricciones de igualdad y restricciones de desigualdad utilizadas en esta investigación, se logró obtener los siguiente:
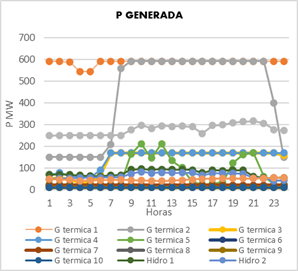
Los resultados del problema de despacho económico realizado mediante la programación no lineal en GAMS nos muestra la potencia activa generada por las unidades térmicas e hidráulicas, el primer modelo de un nodo cuenta como 10 unidades térmicas y 4 unidades hidráulicas. Para el caso de las centrales hidráulicas, ya que esta es un tipo de generación renovable no se tiene un costo variable asociado a la potencia generada, sin embargo, de manera didáctica se tomará en cuenta el costo de oportunidad de agua que estará a 14$/ MW con el fin de obtener el costo económico de dicho tipo de generación, este modelo fue tomado de [9] en donde se muestra la participación de cada una de las unidades.
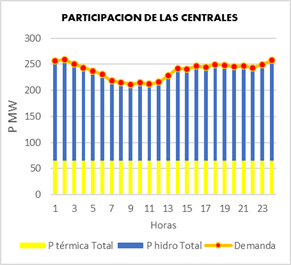
La Figura 4 muestra la potencia de las unidades térmicas e hidráulicas siendo esta la solución que nos determina el menor costo posible teniendo en cuenta todas las restricciones a las que se ha sometido el sistema.
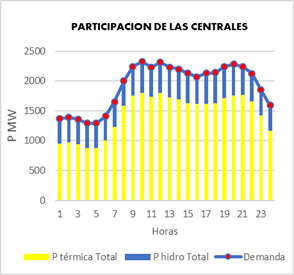
Ya que en esta investigación no se está considerando las pérdidas ni costo de déficit, toda la potencia generada deberá ser igual a la potencia que se demanda en cada hora, en la Figura 5 se muestra de mejor manera el aporte por tipo de tecnología, en donde se observa que para el modelo de un solo nodo se tiene un aporte mayor de las unidades térmicas, se tiene un porcentaje promedio de estas centrales con un 75,132% mientras que las centrales hidráulicas tienen un porcentaje promedio de 24,867%
Esto representa un costo de $748.770 para la parte térmica y para la parte hidráulica $156.220 dando un costo total de la operación de $904.990 dólares como se muestra en la Tabla 10.
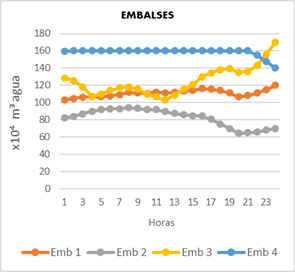
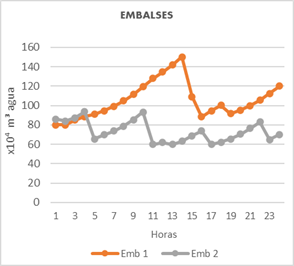
La Figura 6 muestra el nivel de los 4 embalses existentes, el modelo cuenta con embalses conectados hidrológicamente, se observa cómo se cumple con los volúmenes sin excederse del máximo y mínimo de almacenamiento.
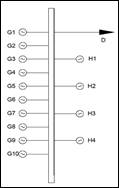
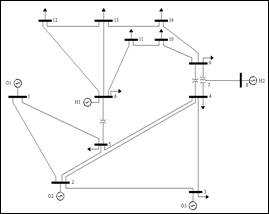
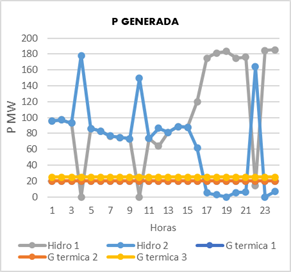
El siguiente modelo resuelto se presenta en el esquema de 14 nodos de la IEEE, en donde originalmente se cuentan con 5 centrales térmicas ubicadas en los nodos 1, 2, 3, 6 y 8, ahora se ubicarán en los nodos 6 y 8 dos centrales hidráulicas reemplazando las térmicas existentes, el planteamiento en el modelo se realiza en base a que existe una escasez de modelos abordando líneas de transmisión, por lo cual el escogió al de sistema 14 nodos ya que esta es una buena alternativa para representar sistemas de mediana escala. Dicho esto, se puede observar en la Figura 7 la potencia activa generada por las unidades, en donde se el sistema opera dentro de los límites máximos y mínimos establecidos.
De igual manera que en el caso anterior, no se consideran las pérdidas y costo de déficit, por lo tanto, en la Figura 8 se muestra el aporte por tipo de tecnología, en donde en este caso observa que para el modelo de 14 nodos se tiene un aporte mayor de las unidades hidráulicas, por parte de las centrales térmicas se tiene un porcentaje promedio de 27,445% mientras que las centrales hidráulicas tienen un porcentaje promedio mayor de 72,554%.
Esto representa un costo de $71.727,360 para la parte térmica y para la parte hidráulica $58.074,8 dando un costo total de la operación de $129.802,16 como se muestra en la Tabla 11.
La Figura 9 muestra el nivel de los embalses ubicados en los nodos 6 y 8, cabe mencionar que en este caso cada central hidráulica tiene su embalse independiente del otro, así mismo cumplen con los niveles máximos y mínimos de almacenamiento.
Tabla 10: Resultados del despacho económico para el modelo de un nodo
| Detalle | Valor obtenido en GAMS | Valores propios de bibliografía [9] | Error porcental |
|---|---|---|---|
| Costo Térmico | $748.770 | $702.306 | 6.61% |
| Costo Hidroeléctrico | $156.220 | - | - |
| Total | $904.990 | $702.306 | - |
Siendo este un modelo propio de [9], en la investigación resuelven el problema utilizando algoritmos genéticos, en el cual se observa como en el despacho económico no se cumplen con algunas restricciones de potencia de los generadores, en la investigación el mínimo de generación es de 10 MW sin embargo el modelo despacha 0 MW en algunos generadores lo que evidentemente no cumple estrictamente con las restricciones que se le impusieron.
Por consiguiente, el modelo desarrollado mediante programación no lineal muestra un despacho económico cumpliendo con todas las restricciones por lo que brevemente se expondrá lo siguiente:
El problema resuelto por [9] muestra un costo de las centrales térmicas de $702.306 mientras que el modelo resuelto en GAMS muestra un costo de $748.770, existe una diferencia de $46.464 la cual se justifica con la participación de todas las centrales térmicas, ya que su límite no permite que estas dejen de operar el deben estar generando el mínimo permitido, esto representa el costo adicional que se menciona.
Tabla 11: Resultados del despacho económico para el modelo de 14 nodos
| Tipo | Costo de Generación [$] |
|---|---|
| Termoeléctrico | $71.727,360 |
| Hidroeléctrico | $58.074,8 |
| Total | $129.802,16 |
En síntesis, el modelo de 14 nodos, presenta dentro del despacho de 24 horas un coste total de $129.802,16. Divididos en $71.727,360 de la parte térmica y $58.074,8 de la parte hidráulica. Mientras que el modelo de un nodo presenta $904.990. Divididos en $748.770 para la generación termoeléctrica y $156.220 para la generación hidroeléctrica.
Ambos modelos difieren por un costo de 775.187,84$. Esto no solo por el tipo de sistema, sino también influyen la demanda y principalmente la participación de las centrales térmicas, en ambos casos el costo térmico es más elevado debido a su naturaleza y costo de combustible elevado. La solución obtenida de GAMS muestra que se encontró el óptimo local, es decir, la función objetivo es muy precisa, mientras que los valores de las variables son menos precisos debido a una función objetivo plana en el interior del área factible, dicho lo anterior, se puede decir que la calidad de la solución es satisfactoria.
CONCLUSIONES Y RECOMENDACIONES
Las operaciones de los sistemas eléctricos de potencia varían según su planificación en diferentes momentos. En la literatura científica, se utilizan modelos matemáticos de optimización, como PL, PNL, MILP, MILNP, y también métodos metaheurísticos, como algoritmos genéticos y enjambres de abejas. La mayoría de las investigaciones sobre la coordinación de los sistemas eléctricos de potencia utilizan métodos metaheurísticos debido a la naturaleza no lineal de la optimización. Sin embargo, también existen modelos exactos, como la programación entera lineal para la planificación de la expansión, la programación no lineal para minimizar las pérdidas en la red y la programación lineal para la coordinación de la operación de los sistemas eléctricos de potencia, que consideran restricciones lineales.
En esta investigación, se utiliza PNL junto con el solucionador CONOPT para resolver el problema de coordinación hidrotérmica. La calidad de los resultados obtenidos para ambos casos se muestra satisfactorios ya que en ambos se encuentra el óptimo local, debido a las restricciones de los sistemas modelados en esta investigación. Para el modelo de un nodo muestra una participación promedio de 24,867 % por parte de las centrales hidroeléctricas, con respecto a las centrales térmicas estas tienen un porcentaje menor debido a que solo son 4 unidades en comparación a las 10 térmicas que existen, sin embargo, el modelo cumple con las restricciones y en efecto, minimiza la participación de la generación térmica. De igual manera para el modelo de 14 barras, la generación hidroeléctrica en este caso representa un 72,554%, logrando concluir que los modelos cumplen con su función objetivo, satisfaciendo sus restricciones. Sin embargo, el hecho de no haber encontrado el óptimo global no implica que la solución se inexacta, existe la posibilidad de que haya soluciones aún más eficientes y rentables fuera de ese rango específico de restricciones impuestas en cada caso. Esto sugiere que se puede realizar futuras investigaciones estableciendo un análisis más exhaustivo y considerar diferentes enfoques o algoritmos para explorar un espacio de soluciones más amplio y encontrar el óptimo global.
El uso de la programación no lineal frente al problema de despacho hidrotérmico muestra resultados satisfactorios, esto debido a que se conocen los parámetros de demanda y condiciones operativas, sin embargo condiciones como la demanda o el flujo de entrada de los embalses no puede ser exacto debido a la variación que se tiene, por tanto ahí la importancia de utilizar modelos determinísticos que permitan predecir estos aspectos con referente a un histórico, si bien el modelo no lineal proporciona resultados sin violar restricciones, el incorporar los modelos heurísticos y metaheurísticos proporcionará al modelo una aproximación frente al pronóstico de los parámetros desconocidos. Por tanto, se recomienda utilizar los modelos utilizados en esta investigación para la corroboración o implementación de los nuevos modelos probabilísticos.