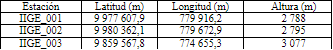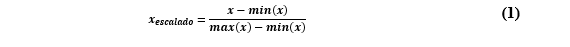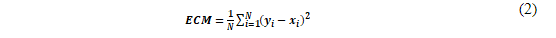Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El rápido crecimiento de tecnologías de generación por aprovechamiento de la energía solar, requieren de técnicas de procesamiento cada vez más elaboradas para entender la variabilidad en el comportamiento del recurso solar en pequeños instantes de tiempo [1].
La energía solar fotovoltaica es una fuente renovable intermitente que puede considerarse como una serie temporal no estacionaria [2]. Existen diversos métodos de predicción de series temporales con modelos estadísticos, numéricos y de inteligencia artificial (IA), basados en el comportamiento físico de la atmósfera [1], [3]. Estos métodos pueden ser del tipo de predicción autoregresivo (AR) y sus variantes como el Método Autoregresivo de Promedio Móvil (ARMA) o el método Autoregresivo Condicional de Heterocedasticidad (ARCH), como se explica en los trabajos de Laily et al. [4] y Bettiza [5]. Estas metodologías son univariables y generalmente trabajan bien con series temporales estacionarias [6]. Los métodos de aprendizaje automático con inteligencia artificial, como las redes neuronales, permiten involucrar en el modelo otras variables relevantes al momento de predecir una serie temporal estacionaria, o no estacionarias [7], [8].
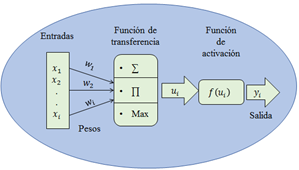
Una Red Neuronal Artificial (RNA) es un modelo computacional inspirado en el funcionamiento de una neurona biológica [9]. La red se compone de una serie de procesadores (neuronas) que se distribuyen en niveles o capas interconectadas [10]. Las neuronas procesan señales de entrada y generan una salida, se comunican unas con otras mediante la intensidad de la fuerza entre sus conexiones [11]. En consecuencia, una neurona artificial es un procesador que interactúa con otras neuronas formando una red, cuyo objetivo es resolver un problema específico. En la Figura 1 se observa la estructura general de una neurona artificial [12].
Entre las diferentes arquitecturas de las RNA, las Redes Neuronales Recurrentes (RNR) tienen aplicaciones en clasificación de patrones y predicción que involucran diversas variables como es explicado en los trabajos de Septiawan et al. [7] y Kamanditya et al. [13].
Las RNR se componen de unidades neuronales, donde la información viaja desde la capa de entrada hasta la capa de salida con retroalimentación o memoria de eventos pasados, lo que significa que las señales se transmiten de vuelta a una neurona o capa anterior de la red [14], [15]. Esta retroalimentación en las neuronas permite obtener mejores soluciones con sistemas no lineales por su capacidad de representar sistemas dinámicos, como series temporales no estacionarias[16], [17]. Las Redes Neuronales Recurrentes Elman (RNRE) y Redes Neuronales Recurrentes Jordan (RNRJ) son un tipo de RNR que utiliza solo el estado del instante anterior de la salida en la capa de contexto para la predicción de variables.
El objetivo de esta investigación es evaluar y comparar los modelos de predicción de RNRE y RNRJ para la estimación de la radiación solar y temperatura en tres estaciones meteorológicas ubicadas en el Ecuador. El artículo es organizado de la siguiente manera. En la sección dos se presenta la metodología utilizada para predicción de las series temporales de temperatura y radiación por RNRE y RNRJ. En la sección tres, se muestran los resultados obtenidos mediante figuras y cuadros estadísticos comparativos de los dos métodos de predicción. Finalmente se presentan las conclusiones y recomendaciones del trabajo.
METODOLOGÍA
La metodología de este trabajo se divide en cuatro secciones. Datos y materiales, identificación de datos atípicos en los datos de análisis, aplicación de RNRE y RNRJ en predicción y criterios de selección del método de predicción por RNR.
Datos y materiales
Los datos usados provienen de 3 estaciones meteorológicas ubicadas en las Provincias de Pichincha y Tungurahua en el Ecuador. El detalle de la ubicación de las estaciones se muestra en la Tabla 1.
En la Tabla 2 se observa el periodo de análisis de los datos de las estaciones meteorológicas. Del periodo de análisis utilizado, los datos se dividieron en dos secciones, el 75 % de los datos fueron usados para el entrenamiento de la RNR y el 25 % restante para la validación del modelo.
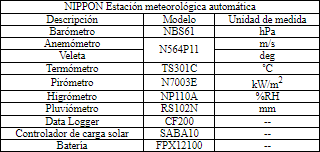
La especificación de las estaciones meteorológicas de la Tabla 1, es detallada en la Tabla 3.
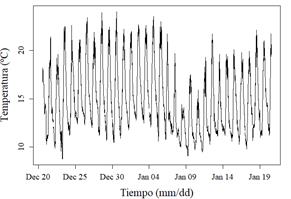
La frecuencia de registro de datos es diezminutal, por lo que en un día completo de medición se obtendrán 144 muestras. El comportamiento de una serie de radiación solar y temperatura ambiente para la estación meteorológica IIGE_001 de un mes de datos, se muestra en la Fig. 2 y la ¡Error! No se encuentra el origen de la referencia. 3.
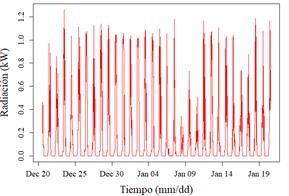
Figura 2: Serie temporal de radiación solar de la estación IIGE_001, periodo 20/12/2020 - 19/01/2021
Para el análisis de los datos provenientes de las estaciones meteorológicas y para la predicción de radiación solar y temperatura se utilizó el software estadístico RStudio (Versión 1.1.456) con compilador en R (versión 3.6.3). Además, la simulación de las redes RNRE y RNRJ usaron la librería RSNNN [18].
Identificación de datos atípicos
Los datos provenientes de las estaciones meteorológicas pasan por un tratamiento en la cual se evalúa la calidad de las mediciones registradas por los sensores. Las mediciones presentan datos inusuales o anómalos se los conoce como atípicos y no son considerados para el entrenamiento de la red neuronal.
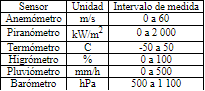
La identificación de los valores atípicos se basa en encontrar valores que no cumplan los límites de medición de los sensores de la estación meteorológica, los cuales son presentados en la Tabla 4.
Además, se consideraron los valores que no se registraron por falla en los sensores, pérdida de energía o mantenimientos en la estación.
Aplicación de RNRE y RNRJ en predicción.
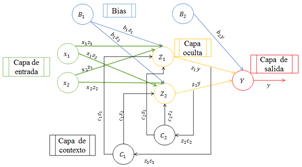
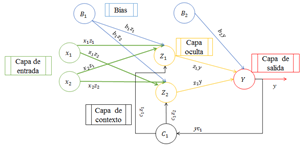
Una RNR se caracteriza por tener una capa de contexto en donde parte de información se retroalimenta como una nueva entrada, esto permite que la red tenga mayor capacidad de aprendizaje al reconocer y generar patrones [5]. Lo que diferencia una RNRE de una RNRJ es que la retroalimentación en Elman va desde la salida de la capa oculta hacia la capa de contexto, en cambio en Jordan la retroalimentación ocurre desde la capa de salida hasta las neuronas de la capa de contexto. La arquitectura básica de una RNRE y RNRJ se observa en la Figura 4 y Figura 5, respectivamente.
Las RNRE tienen en su celda de contexto igual número de capas y neuronas que la capa oculta, en cambio, las RNRJ tienen en la capa de contexto el mismo número de neuronas que la salida.
Por la arquitectura de la red neuronal recurrente de tipo Elman, el tiempo computacional que se requiere para el entrenamiento será mayor que una red neuronal recurrente de tipo Jordan. Esto se debe a que la recurrencia de la RNRE se toma de las salidas de las neuronas de las capas ocultas y no de las capas de salida como en una RNRJ, donde el número de neuronas de las capas ocultas siempre fue mayor a las dos neuronas de la capa de salida.
El número de entradas de la RNR varió entre tres a siete neuronas; de las cuales la fecha (F), temperatura (T) y radiación (I) solar fueron variables fijas en el análisis. Además, las variables de velocidad de viento (V), humedad relativa (H), precipitación (R) y presión atmosférica (P) son variables que se probaron en modelo de predicción para temperatura ambiente y radiación solar. La predicción de los datos se realizó para dos días futuros, es decir, para los siguientes 288 diezminutales. La Estación IIGE_003 presentó lecturas anómalas en la serie temporal de humedad relativa, por lo que en este caso no se utilizó la variable H.
Las variables meteorológicas utilizadas para el análisis fueron escaladas en valores entre 0 y 1 como se muestra en (1), debido a los procesos de aprendizaje de la red. Cuando se obtienen los valores de salida de la red neuronal, los datos pasan por el proceso inverso de normalizado.
Donde, x escalado son los valores de la serie escalada y 𝒙 los valores meteorológicos usados en el análisis.
El entrenamiento de la RNRE se realizó con una y dos capas ocultas con combinaciones entre cuatro y doce neuronas. En la RNRJ se utilizó una capa oculta con variaciones entre cuatro y doce neuronas.
Además, se utilizaron tres algoritmos de aprendizaje distintos; Retropropagación (RP), Retropropagación de momento (RPM) y Retropropagación Resiliente (RPR), como se detalla en [18]. El algoritmo de RP propaga la señal del error hacia atrás permitiendo calcular el cambio del valor de los pesos en las capas anteriores en base a la minimización de la función de coste, en este caso mediante el descenso del gradiente de la función del error [19]. En RPM se introduce un término de momento que permite reducir las oscilaciones en el descenso del gradiente [20]. La diferencia entre RPR con algoritmos de propagación hacia atrás es que la derivada de la función del error se usa para determinar el sentido en el que los pesos deben ser corregidos y no para el cambio de su magnitud [21],[22].
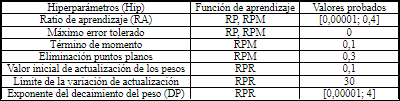
Cada función de aprendizaje tiene hiperparámetros (Hip) específicos que fueron usados en el intervalo mostrado en la Tabla 5. En RP y RPM se varía los valores de la tasa de aprendizaje mientras que en RPR se varía los valores del exponente del decaimiento del peso (DP), los demás hiperparámetros permanecieron como valores constantes.
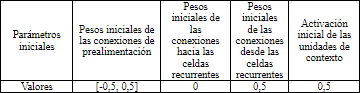
En la Tabla 6 se observan los parámetros de inicialización de la red. Los valores de los pesos iniciales en las conexiones que se propagan hacia adelantes son seleccionados aleatoriamente entre un intervalo de [-0,5; 0,5].
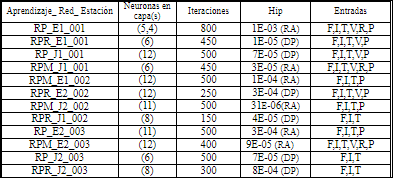
De las pruebas realizadas se seleccionaron doce RNR, seis de tipo Elman y seis de tipo Jordan. Los parámetros de entrenamiento utilizados para cada red se observan en la Tabla 7. Las etiquetas de las doce RNR, ubicadas en la primera columna, están escritas de la siguiente manera, F.Aprendizaje_Tipo de red_Estacion ► RP_E1_001
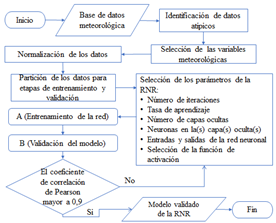
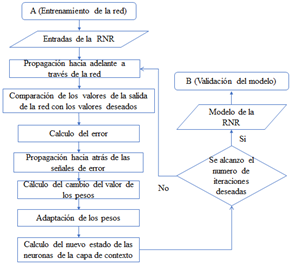
Definidos los parámetros e hiperparámetros de la RNR, se entrena la red el número de iteraciones deseadas hasta obtener el valor final de los pesos para el modelo. Durante cada iteración de la red las señales son propagadas desde la capa de entrada hacia las capas ocultas y después a la capa de salida, después, se realiza una actualización síncrona de las unidades de contexto. Al final de cada iteración se calcula la Suma de los Errores Cuadrados (SSE por sus siglas en ingles), el cual puede considerarse como el primer indicador de rendimiento de la red antes de su etapa de validación.
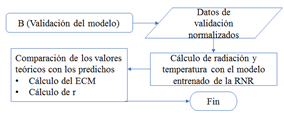
En la etapa de validación se consideró una correlación de Pearson mayor a 0,9 para validar el modelo, donde, según el trabajo de M. De Liu et al. [23], un valor mayor a 0,98 se considera como excelente resultado. Con los pesos sinápticos establecidos en modelo entrenado de la red, se obtienen las salidas de radiación y temperatura con el 20% de los datos de cada estación usados para la etapa de validación. Los datos de salida o los datos predichos son comparados con las salidas teóricas mediante los indicadores de rendimiento de la sección 2.4.
El proceso de predicción, entrenamiento y validación para una RNRE o RNRJ se muestran en la Figura 6, Figura 7 y Figura 8, respectivamente [6], [7], [24].
Criterios de selección del método de predicción por RNR
Para evaluar el rendimiento de la predicción de radiación solar y temperatura se usaron dos indicadores apreciados en (2) y (3), el error cuadrático medio (ECM) [25] y el coeficiente de correlación de Pearson (r) [23], comparado entre los valores medidos y los valores obtenidos predichos por los modelo.
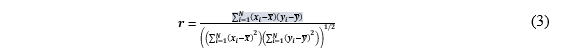Donde 𝒙 𝒊 es el valor medido por el sensor, 𝒚 𝒊 es el valor predicho por el modelo, 𝑵 es el número de datos, 𝒙 y 𝒚 son las medias aritméticas de las variables 𝒙 y 𝒚, respectivamente.
ANÁLISIS DE RESULTADOS
Cada modelo de red RNRE y RNRJ mostrado en la Tabla 7, pasó por una etapa de validación de resultados y por una etapa de predicción. En ambas etapas los modelos se evaluaron con 2 indicadores de rendimiento, la correlación de Pearson y el error cuadrático medio.
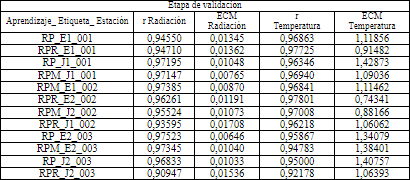
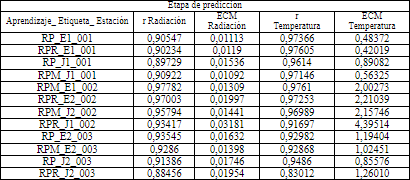
En la Tabla 8, se observa los valores de r y ECM de los modelos evaluados en la etapa de validación de datos.
Los valores de correlación r en radiación y temperatura superan 0,91 y los valores de ECM no superan los 0,018 kW en radiación solar y 1,43 ˚C en temperatura ambiente.
Los valores más altos de r en la etapa de validación de datos de radiación solar y temperatura ambiente son en su conjunto los del modelo RPM_J1_001, en la Tabla 8.
En la Tabla 9, se aprecian los valores de r y del ECM en la etapa de predicción para dos días posteriores.
Los valores de correlación más altos de r de la estación IIGE_001, IIGE_002 y IIGE_003 son respectivamente los modelos RPM_J1_001, RPM_E1_002 y RP_E2_003, en la Tabla 9. La arquitectura seleccionada para la predicción en las tres estaciones meteorológicas, depende del comportamiento de las series temporales de análisis.
Los valores más altos de r en la etapa de predicción de datos de radiación solar y temperatura ambiente son en su conjunto los del modelo RPM_E1_002, en la Tabla 9.
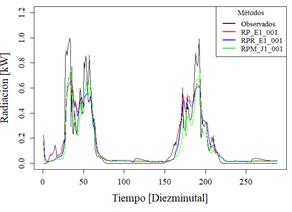
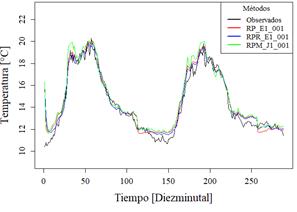
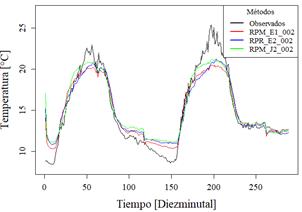
En la Figura 9 se observan la gráfica de predicción de radiación solar y en la Figura 10 la gráfica de temperatura ambiente, ambos de la Estación IIGE_001
En el comportamiento de las predicciones de radiación solar, los valores no llegan a 0 como mínimo valor de radiación, el cual es rectificado en base al comportamiento de la serie temporal (radiación=0 en horas nocturnas). Se observa una limitación en los métodos para alcanzar los mínimos y máximos de los valores observados.
El comportamiento de temperatura ambiente de las predicciones se ajusta con similitud a las medidas tomadas por el sensor.
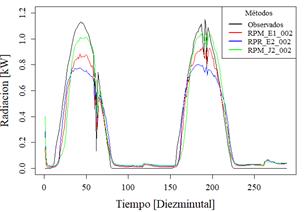
En la Figura 11 se observan la gráfica de predicción de radiación solar y en la Figura 12 la gráfica de temperatura ambiente, ambos de la Estación IIGE_002.
En el comportamiento de las predicciones de radiación solar, se observa un comportamiento similar al de la Estación IIGE_001, los valores no alcanzan el mínimo de 0 en radiación ni los valores máximos.
El comportamiento de temperatura ambiente de las predicciones se ajusta a las medidas tomadas por el sensor, sin embargo, se observan limitaciones al llegar a los valores máximos y mínimos de temperatura.
CONCLUSIONES Y RECOMENDACIONES
Los modelos de RNR Elman y Jordan muestran convergencia con un número de iteraciones entre 300 y 600. El tiempo computacional empleado en el entrenamiento de cada modelo se relaciona directamente con la cantidad de datos del set y el número de iteraciones al entrenar la red, si estas variables aumentan el tiempo computacional también. Se pudo observar que, si las iteraciones son superiores a 600, los resultados de la correlación de Pearson varían en aproximadamente ±2 %.
Los resultados en la etapa de validación para las tres estaciones meteorológicas mostraron coeficientes de correlación mayores a 0,92 en temperatura y radiación solar para las RNRE y RNRJ. Esto demuestra que el entrenamiento de las redes se ajusta al comportamiento de las series temporales.
Para la etapa de predicción, en la estación IIGE_001, el mejor resultado se obtuvo con una RNRJ con aprendizaje RPM. En la estación IIGE_002, el mejor resultado fue con una RNRE con aprendizaje RPM. En la estación IIGE _003, se obtuvieron dos resultados similares, uno con RNRJ y el otro con RNRE, ambos con algoritmo de aprendizaje RP. Los resultados demuestran que se puede entrenar satisfactoriamente una RNRE o una RNRJ para aplicaciones de predicción de series temporales.
En las gráficas de predicción de radiación solar, se tienen valores de radiación positivos en horas nocturnas. Estos valores no son altos, pero afectan el comportamiento esperado de la predicción, por lo que es importante realizar una depuración previa a la publicación del resultado, como una propuesta al implementar los métodos en una situación de seguimiento de recurso solar.
Los valores de correlación más altos bajo los parámetros de entrenamiento de las RNRE y RNRJ en la etapa de validación, tuvieron el mejor comportamiento en la etapa de predicción. Esto permite afirmar que la parametrización con mejores resultados en la etapa de validación, deberán ser los seleccionados para el modelo predictivo.
