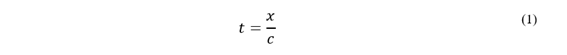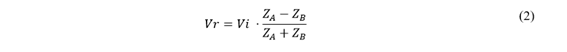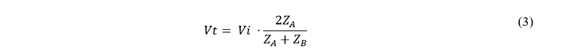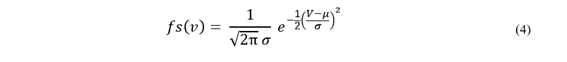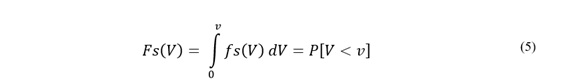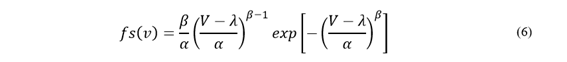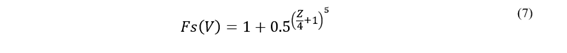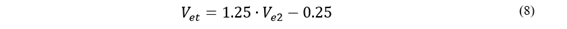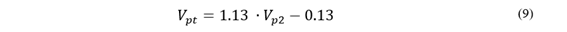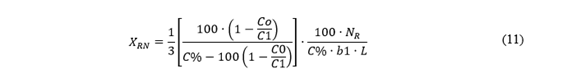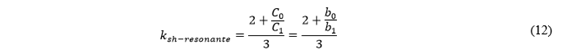INTRODUCCIÓN
La implementación de la interconexión Ecuador-Perú surge con el compromiso de la integración eléctrica regional y aprovecha la complementariedad hidrológica para realizar intercambios de energía entre ambos países. También se garantiza la integración de los futuros proyectos de generación que se desarrollan tanto en Ecuador como en Perú [1]. Esta interconexión se realizará a nivel de 500 kV desde la S/E Chorrillos hasta la S/E Pasaje en Ecuador y culminando en la S/E Piura en Perú.
La amplitud de las sobretensiones aumenta proporcionalmente en base al voltaje nominal de la red [2]. En sistemas de Extra Alta Tensión (EHV por sus siglas en inglés) las sobretensiones que podrían causar daños significativos, es el caso de la interconexión Ecuador-Perú 500 kV. Luego, la interconexión aumenta la posibilidad de que ocurran afectaciones en la infraestructura eléctrica que resulten de los sobrevoltajes en la red. Estas solicitaciones dieléctricas son alteraciones de potencial de un sistema con tendencia a superar su valor nominal, causadas principalmente por fallas a tierra, eventos de maniobra y descargas atmosféricas [2]. La exposición a esta elevación de tensión produce un desgaste en el aislamiento de los equipos que componen el sistema eléctrico de potencia (SEP).
Debido a la gran cantidad de parámetros que intervienen durante las sobretensiones de maniobra y su carácter aleatorio, es común utilizar métodos estadísticos para determinar la amplitud de las solicitaciones dieléctricas resultantes con alta probabilidad de aparecer en el sistema al momento de energizar la red, considerando como variable aleatoria continua a las sobretensiones que puedan ocurrir. La distribución normal o Gaussiana es la más utilizada en este tipo de análisis, tal y como se presenta en [3], [4] donde se aplica esta distribución para analizar sobretensiones por maniobra en EHV obteniendo resultados cercanos a los propuestos en las normativas IEEE 1313 e IEC 60071 [5], [6].
El trabajo de [7] sugiere utilizar la distribución de Weibull en lugar de la distribución Gaussiana, debido a que las expresiones de Weibull modificadas están definidas por los mismos parámetros que caracterizan a las expresiones gaussianas (media y desviación estándar). Además, en el Anexo C de la IEC 60071-2 [6], se recomienda utilizar la función de probabilidad modificada de Weibull tanto para el cálculo de sobretensiones como para determinar la descarga disruptiva de aislamiento. A pesar de esto, la mayoría de estudios se enfocan en utilizar la distribución Gaussiana para el cálculo de sobretensiones y en general para distintitas variables continuas. Sin embargo, se debe tener especial cuidado al suponer para una situación dada un modelo de probabilidad normal sin previa comprobación o comparación. Por ello, diversos estudios tales como [8], han comparado distintas distribuciones de probabilidad existentes para evaluar diversos fenómenos en su propio campo, por ejemplo, en la evaluación del potencial de energía eólica. llegando a la conclusión de que ambas distribuciones arrojan resultados aceptables.
En estudios de coordinación de aislamiento se requiere conocer la distribución estadística de sobretensiones y la confiabilidad de sus parámetros. En este trabajo se compara la aplicación de las distribuciones estadísticas Gaussiana y de Weibull modificada, a partir de las sobretensiones generadas en maniobras de energización mediante la herramienta de simulación ATPDraw, con la finalidad de determinar la magnitud de las sobretensiones fase-fase y fase-tierra con alta probabilidad de presentarse. Las principales contribuciones de este trabajo se detallan a continuación:
Se presenta un modelo la interconexión Ecuador-Perú 500 kV usando el software ATPDraw.
Se muestra el procedimiento para desarrollar la simulación de sobretensiones de maniobra por energización en el sistema de EHV de 500 kV.
Se comparan los resultados obtenidos a partir de las distribuciones estadísticas Gaussiana y de Weibull para sobretensiones de maniobra por energización.
El resto de este documento se organiza como sigue, en la Sección II, se revisan los fundamentos teóricos para el estudio estadístico de sobretensiones. Luego, en la Sección III se muestra la metodología utilizada para modelar el sistema y simular las sobretensiones de maniobra. En la Sección IV se presentan los resultados del análisis estadístico de las sobretensiones en la red. Finalmente, en la Sección V se exponen las conclusiones del trabajo.
MARCO TEÓRICO
En la coordinación de aislamiento es fundamental determinar la magnitud de las sobretensiones para seleccionar apropiadamente el aislamiento eléctrico que deberá estar en capacidad de soportar las solicitaciones dieléctricas durante la operación del sistema. A continuación, se revisan los fundamentos teóricos necesarios para estudiar las sobretensiones de la red.
Ondas Viajeras
Cuando se producen perturbaciones en las líneas de transmisión ya sea por fallas, maniobras o descargas atmosféricas, se generan ondas de corriente y voltaje, a estas ondas resultantes se las conoce como ondas viajeras, las cuales presentan velocidades aproximadas al desplazamiento de la luz con tiempos de propagación en el orden de los us (microsegundos). Se puede efectuar el cálculo del tiempo de propagación de onda en función de la longitud de la línea de transmisión evaluada mediante la Ecuación (1) [9].
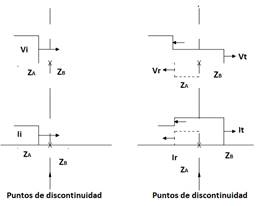
Las ondas viajeras se propagan a lo largo de la línea hasta llegar a un punto de discontinuidad que está determinado por un cambio en la estructura geométrica o medio de la línea de trasmisión, este cambio produce una variación de parámetros de impedancia característica de la línea transmisión 𝑍 𝑐 , que determina el desplazamiento de la onda, esto se ilustra en la Fig. 1, donde se representan el comportamiento de las ondas viajeras al encontrarse con el punto de discontinuidad y las impedancias características ZA y ZB separadas por el punto de discontinuidad. Es en este punto de discontinuidad la onda viajera inicial o incidente Vi se divide en onda reflejada Vr y transmitida Vt, que obedecen a las expresiones descritas en la Ecuación (2) y Ecuación (3) respectivamente [10].
Entonces, la magnitud de la onda transmitida y reflejada depende del valor de ZA y ZB. Luego, si se evalúa el caso más severo de reflexión de onda, donde 𝑍 𝐵 →∞, se presenta un circuito abierto y consecuentemente la onda es reflejada en su totalidad, adicionándose a la onda incidente de tensión, lo que representa una significativa sobretensión en el extremo abierto de la línea [10].
Fuente: [11]
Sobretensiones por Maniobra
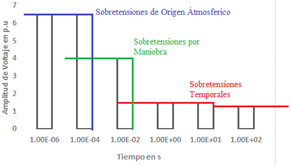
Las sobretensiones vienen definidas por su amplitud, tiempo de impulso y frecuencia de oscilaciones; y pueden ser de origen atmosférico, de maniobra o temporales como se identifica en la Figura 2. Las sobretensiones por maniobra (SOV por sus siglas en inglés) se usan para dimensionar el aislamiento en sistemas con voltaje nominal superior a 242 kV. Su origen es interno, de naturaleza oscilatoria y ocasionadas generalmente por la acción de apertura o cierre de los interruptores de potencia [12].
Fuente: [13]
Los parámetros de estudio de sobretensiones dependen de la capacidad de cortocircuito en el lugar donde se ha conectado la línea y del instante en el que ocurre la unión en los contactos de los interruptores. Este instante es una variable aleatoria, por lo que el nivel de sobrevoltaje en el momento de encendido de la línea también es una variable aleatoria [3]. Las sobretensiones por maniobra se dan en líneas de transmisión, transformadores, bancos de reactores o condensadores, donde destacan los eventos de energización y reenganche de estos elementos [9].
Distribución Estadística de Sobretensiones
Para un correcto análisis estadístico se deben considerar a las sobretensiones como una variable aleatoria continua, ya que puede tomar un número infinito de valores de voltaje entre un intervalo definido [15]. Esto sumando a la gran cantidad de variables a analizar, resulta complejo caracterizar, por lo que, para tener una aproximación mayor al comportamiento real de las sobretensiones se suelen aplicar distribuciones estadísticas, también denominadas distribuciones de probabilidad [2]. Generalmente, un análisis estadístico de sobretensiones debe considerar tres aspectos:
Selección de una distribución estadística para todas las variables de carácter aleatorio.
Dependiendo de la sobretensión a calcular, se desarrolla un modelo matemático para el sistema de estudio.
Aplicación de un modelo de estudio estadístico, donde usualmente se usa el método de Monte Carlo que es un procedimiento iterativo de variables aleatorias.
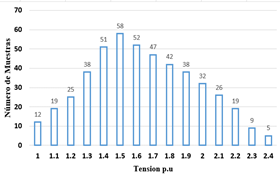
La distribución estadística de sobretensiones originada por eventos de maniobra en líneas aéreas se obtiene a partir de un número determinado de maniobras generadas en simulación utilizando un interruptor estadístico en ATPDraw, estos resultados se ordenan para obtener un histograma similar al mostrado en la Figura 3.
Fuente: [2]
Al reorganizarse el histograma de sobretensiones a partir de 𝑛 simulaciones, se obtiene una función de densidad de probabilidad [4], que si se considera una distribución Gaussiana, obedece a la siguiente expresión:
La Ecuación (4) representa la probabilidad de que se presente un determinado valor de tensión dentro de las muestras obtenidas, que resulta en la conocida campana de Gauss y sirve para calcular el riesgo de falla (𝑅) cuando se lo compara con los valores de la distribución acumulativa de aislamientos [2]. Sin embargo, la distribución estadística de sobretensiones también se puede expresar a través de una función complementaria denominada función de distribución acumulativa, presentada en la Ecuación (5), la cual representa la probabilidad de que la sobretensión resultante sea de una amplitud mayor a un valor de tensión dado.
No existe una expresión matemática analítica cerrada para la función de distribución acumulativa gaussiana evaluada con limites + ∞ 𝑦 − ∞, por lo que en la práctica se suelen acotar en intervalos limitados de − + 4 𝜎 a partir del valor medio o a su vez valorar la función de distribución acumulativa con limites desde − ∞ hasta el valor de sobretensión dado, este procedimiento lo realizan programas especializados en análisis de datos [2]. En la Figura 4 se muestra la representación gráfica de los valores de sobretensión por maniobra de las expresiones (4) y (5).
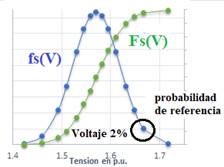
Figura 4: Caracterización de sobretensiones a través de sus funciones de distribución de probabilidad
Debido a la simplicidad del procedimiento, con una precisión aceptable en los resultados, la utilización de la distribución normal o Gaussiana es empleada en todo tipo de aplicaciones que estén involucradas con variables continuas de naturaleza oscilatoria, en este caso esta variable es el valor de sobretensiones. Alternativamente, al considerar variables de este tipo también se puede emplear la función de densidad de probabilidad de Weibull [15], mostrada en la Ecuación (6):
Donde:
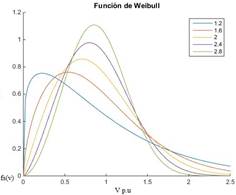
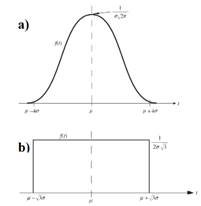
Cuando se considera valores de 𝜆=0 y 𝛼=1, la forma de la función de Weibull se asemeja a una campana, similar a la forma clásica de la distribución gaussiana, esto se da para valores positivos de 𝛽>2, como se muestra en la Fig. 5. Estos valores son recomendados por [2] debido a que las sobretensiones por lo general presentan un pico de resultados y luego decrecen, asemejándose a un campana estadística tradicional.
También, se puede emplear una distribución de Weibull modificada en función de los parámetros de 𝜇 y 𝜎. En la Ecuación (7) se muestra la función de distribución acumulativa, que parte de la función de densidad de probabilidad de Weibull, adaptada por [2] empleando el parámetro 𝑍.
Donde, 𝑍= 𝑉−𝜇 𝜎 , es el parámetro adaptado para la distribución de Weibull modificada, y 𝑉 es el valor de la tensión a ser evaluada en la función de distribución acumulativa de Weibull.
METODOLOGÍA
En este documento se toma como caso de estudio el Sistema de 500 kV de Ecuador. Para modelar los elementos del SEP en el software ATPDraw se tomaron los valores de referencia expuestos en [1] y el procedimiento de coordinación de aislamiento de la IEC 60071-2 [13]. Para la evaluación de los resultados de la distribución estadística de probabilidad, en [6] se proponen dos métodos:
Método Fase-Pico: En cada operación de maniobra se escoge el valor pico fase tierra de cada fase que compone la red, lo que contribuye con tres resultados de valores pico.
Método Caso-Pico: De cada operación de maniobra se escoge el valor pico fase-tierra más alto de las tres fases.
Una vez seleccionado el método, se debe tener en cuenta que, sin pararrayos la sobretensión viene dada por la amplitud, con una probabilidad 𝑓𝑠(𝑉)= 2%, de ser sobrepasada o del 98% de ocurrencia si se usa 𝐹𝑠 𝑉 [6]. A partir de estas consideraciones, se obtienen los valores de las sobretensiones 𝑉 𝑒2 (fase-tierra) y 𝑉 𝑝2 (fase-fase). También, se considera la desviación estándar 𝜎, el valor medio 𝜇 y el valor de sobretensiones de truncamiento, que es la más elevada que se puede presentar en el sistema tanto 𝑉 𝑒𝑒 (fase-tierra) como 𝑉 𝑝𝑡 (fase-fase) representados en las Ecuaciones (7) y (8) respectivamente [6].
Modelos de Líneas de Transmisión
Para determinar el modelo de línea más adecuado para la simulación, se consideran cuatro elementos:
exactitud del modelo.
tiempo de respuesta computacional.
la capacidad del modelo de simular líneas con alta simetría (transposiciones).
la complejidad del modelo para el estudio.
Además, se debe tener en cuenta que, para estudios de sobretensiones se consideran parámetros distribuidos dependientes de la frecuencia, debido a que, en las líneas de transmisión se presentan fenómenos como el efecto skin y el efecto de retorno a tierra a medida que aumenta la frecuencia, para así evaluar de manera más precisa la contribución natural de las perdidas en la línea de transmisión [16].
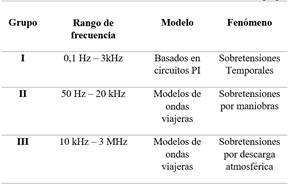
Existen diferentes modelos de líneas de transmisión utilizadas en estudios eléctricos como lo son: modelo Z, idempotente, directo Nguyen, modelo PI, Bergeron y J Martin, sin embargo, en el software ATP se tiene disponibles los tres últimos por lo que se hará especial énfasis en estos. El modelo PI es usado generalmente para simulaciones en estado estacionario de líneas cortas a la frecuencia de la red, por lo que su aplicación se limita a sobretensiones temporales. En cuanto al modelo Bergeron, no es aplicable en este análisis debido a que utiliza matrices de transformación cuyos parámetros contienen ciertas limitaciones para variar en función su frecuencia. Finalmente, el modelo J. Martin es el más utilizado para análisis de sobretensiones por maniobra, ya que ofrece una mayor exactitud en comparación con el modelo Bergeron, a pesar de que, se tiene una respuesta computacional más lenta, y es aplicable para los rangos de frecuencia establecidos en la Tabla 1. Cabe recalcar que, este modelo no es aplicable en bajas frecuencias y para secciones de línea muy cortas. Consecuentemente el modelo J. Martin es usado como modelo estándar de comparación para este tipo de análisis [17].
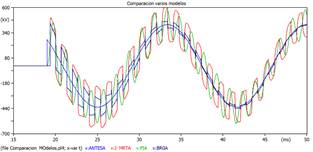
En la Figura 6 se muestra la comparación de la magnitud de voltaje durante una maniobra de energización para los tres modelos de línea, considerando una longitud de 100 km. Donde se puede apreciar que el número de oscilaciones en un ciclo es de 11 en el modelo Bergeron y J. Martin. Nótese que, la magnitud de tensión inferior en el modelo Bergeron. Mientras que, el modelo PI presenta un menor número de oscilaciones con respecto a los demás modelos, pero su magnitud de voltaje no varía considerablemente con respecto al modelo J. Martin.
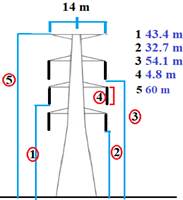
Por otro lado, como se señaló en la Sección 2.1, la geometría de la línea es un factor de relevancia para la propagación de ondas viajeras. En este estudio las dimensiones referenciales de la estructura de transmisión doble circuito para 500 kV se obtuvieron del trabajo de [18] y se muestran a detalle en la Figura 7. Además, de acuerdo a [1], [19] solamente el primer circuito será energizado, hasta evaluar el comportamiento de la red incluyendo la futura entrada al SNI del Sistema de transmisión Santiago.
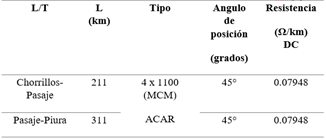
En la Tabla 2, se detallan los parámetros por fase de la línea de transmisión a ser utilizados en la Interconexión Ecuador-Perú 500kV, estos datos son necesarios para determinar valores de impedancia y admitancia en las líneas de transmisión.
Además, la línea presentará transposición de fases. La transposición en líneas con longitudes comprendidas entre 70 y 250 km se debe realizar en un ciclo completo que se compone de tres transposiciones simples en las longitudes 1/3, 3/6 y 5/6 de la línea, mientras que para longitudes mayores a 250 km la transposición se recomienda realizarla en dos ciclos completos que consiste en transposiciones simples en las longitudes 1/3, 3/12, 5/12, 7/12, 9/12, 11/12 [20].
Interruptores de Potencia
La configuración del interruptor de potencia es la pieza clave para un estudio estadístico de sobretensiones en el software ATPDraw, destacándose dos tipos de interruptores con tiempos de ejecución variables y útiles para análisis de sobretensiones [2]:
Interruptor Sistemático: el cierre es calculado de manera ordenada de un instante de tiempo mínimo a un tiempo máximo en incrementos de tiempo semejantes.
Interruptor Estadístico: el tiempo de cierre es calculado de manera aleatoria de acuerdo al tipo de distribución probabilística seleccionada.
Para la configuración del interruptor estadístico se deben considerar dos parámetros suministrados por el usuario, que son: tiempo medio de cierre o apertura (T) y la desviación estándar de tiempos de corte (σ). La selección del tipo de distribución probabilística (gaussiana o distribución uniforme) implica cambios en la dispersión de datos de simulación. Por ejemplo, para una distribución gaussiana se considera 𝑇+𝜎, y para una distribución uniforme 𝑇+ 1 2𝜎 3 , como se aprecia en la Figura 8. Así, se obtiene la variabilidad de datos que tendrá el programa al momento de ejecutar la simulación [15].
Si se escoge una distribución de tipo Gaussiana para evaluar las maniobras, la mayor cantidad de maniobras estará cerca del tiempo medio de cierre dependiendo del valor de desviación estándar. Mientras que, la distribución uniforme reparte la misma cantidad de maniobras a los extremos del tiempo medio en función de la desviación estándar que en este caso toma el nombre de rango de tiempo de amplitud de la distribución uniforme.
Fuente: [2]
Mientras que, para representación de interruptores se tiene en cuenta la relación que tienen los interruptores estadísticos entre sí, se pueden representar de tres maneras diferentes [21]:
Interruptores independientes: usados en simulaciones monofásicas ya, que el tiempo de cierre ( 𝑇 𝑐𝑖𝑒𝑟𝑟𝑒 ) es aplicable únicamente para el interruptor seleccionado.
Interruptores maestros y esclavos: se tiene un interruptor principal con configuración de 𝑇 𝑐𝑖𝑒𝑟𝑟𝑒 inicial, mientras que los interruptores esclavos dependen del tiempo de cierre del interruptor master y también de un tiempo de retardo, mostrados en la Ecuación 9. Se usa en unidades trifásicas, debido a que sus polos suelen estar unidos mecánicamente. Puede haber un retraso mínimo en el tiempo de cierre de los interruptores dependientes o esclavos.
Interruptores referencias (target): el tiempo medio de cierre de un interruptor se toma como referencia para otros interruptores relacionados con él.
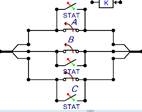
En este estudio se ha seleccionado para cada fase un interruptor estadístico con distribución uniforme, formando así una sola unidad trifásica como se muestra en la Figura 9.
Una aproximación correcta de la distribución estadística de sobretensiones, resulta de someter al sistema a 200 simulaciones para obtener una precisión mayor en el cálculo de sobretensiones por maniobra como se propone en [2] y en [22].
Banco de Reactores Shunt y Reactor Neutro
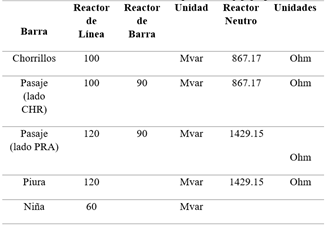
Para compensar los efectos capacitivos que tiene la línea de transmisión, cuando esta se encuentre en vacío o con baja carga se instalan bancos de reactores en paralelo con la línea de transmisión para limitar las sobretensiones, aunque también se pueden conectar directamente en las barras para limitar sobretensiones por apertura y re cierre de líneas. A diferencia de los reactores de barra, los reactores de línea cuentan con un reactor neutro dimensionado en función de las características de la línea [20]. Los parámetros de compensación de línea, de barra y reactor neutro se presentan en la Tabla 3.
El valor de reactor neutro se basa en la Ecuación (10), y cabe resaltar que la compensación debe ser realizada en un grado menor al grado critico de compensación presentado en la Ecuación (12), esto se realiza para evitar efectos de resonancia eléctrica [10].
Equivalente de Red y Configuraciones Adicionales
Resulta poco práctico modelar el SNI completo, y por esta razón para la mayoría de los cálculos se utilizan equivalentes de red, que consisten en la reducción de la red a partir de cálculos de cortocircuito en las barras seleccionadas [23]. Estos valores son clave para realizar simulaciones que proporcionen resultados coherentes y basados en los parámetros del sistema de estudio.
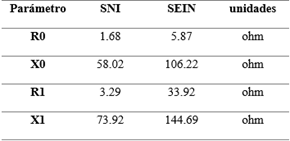
El equivalente de red en la barra Chorrillos se obtuvo a partir del trabajo publicado por [24], mientras que, el equivalente de red en la barra la Niña se obtuvo en base a la información publicada por el Comité de Operación Económica del Sistema Interconectado- Perú (COES) [25]. En la Tabla 4 se muestran los parámetros obtenidos para la red equivalente en la barra de Chorrillos en Ecuador y en la barra de La Niña en Perú.
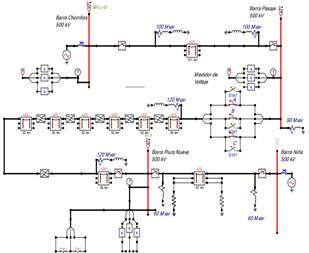
Al realizar la implementación y configuración de los elementos del sistema de estudio mediante el software ATPDraw se obtiene el sistema mostrado en la Figura 10.
RESULTADOS
Para determinar las sobretensiones representativas por maniobra a través de un análisis estadístico, se someterá el sistema de estudio a tres escenarios de energización, en los cuales se verificarán las sobretensiones 𝑉 𝑒2 (fase-tierra) y 𝑉 𝑝2 (fase-fase):
Escenario 1: Energización de líneas de transmisión sin ningún control de voltaje
Escenario 2: Energización de líneas de transmisión con bancos de reactores conectados a la línea.
Escenario 3: Energización de líneas de transmisión con resistencias de pre-inserción de 400 ohm.
Luego, aplicando los factores de conversión (ver Sección 3) se determinan las sobretensiones de truncamiento 𝑉 𝑒𝑡 (fase-tierra) y 𝑉 𝑝𝑡 (fase-fase). En cada escenario se compararán los valores se tensión obtenidos mediante la distribución de Gauss con la distribución de Weibull modificada.
Escenario 1
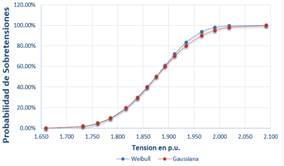
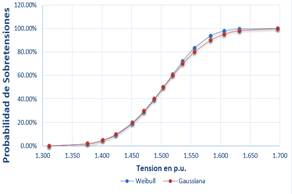
En la Tabla 5 y Tabla 6 se muestran las sobretensiones fase-tierra y entre fases al energizar las líneas sin ningún tipo de control de voltaje, comparando los resultados entre la distribución Gaussiana y Weibull. La diferencia entre ambas distribuciones para el voltaje estadístico Ve2 de la L/T CHR-PSJ es de 2.8% y en la L/T PSJ-PRA es de 5.3% en sobretensiones fase-tierra.
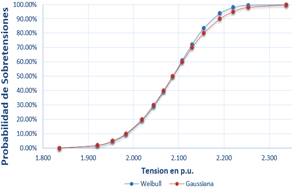
Las Figura 11 y Figura 12 comparan las funciones de distribución Gaussiana y de Weibull para el Escenario 1 en la línea de transmisión CHR-PSJ y PSJ-PARA respectivamente.
Escenario 2
En la Tabla 7 y Tabla 8 se muestran los resultados de sobretensiones utilizando al banco de reactores con los valores establecidos en el PET, junto con los resultados de comparación de distribución estadística Gaussiana y Weibull. En este caso, la variación entre ambos métodos fue de 2% para la L/T CHR-PSJ y 5% en la L/T PSJ-PRA.
Tabla 7:/Tabla 8: Resultados Escenario 2 de sobretensiones fase-fase Vp2 y Vpt
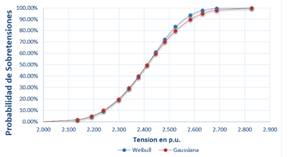
De manera análoga al Escenario 1, En la Figura 13 y la Figura 14 se comparan las funciones de distribución Gaussiana y de Weibull para el Escenario 2 de las dos líneas de transmisión en análisis.
Escenario 3
Para la evaluación del escenario 3 se utilizaron resistencias de pre-inserción que por lo general en los SEP pueden tomar valores de 300, 400 y 500 ohm, en este caso se ha seleccionado 400 ohm. De manera análoga a los dos casos anteriores, en la Tabla 9 y Tabla 10 se presentan variaciones en la distribución estadística de Weibull con respecto a Gauss en el orden de 2.5% y 3.1% para la L/T CHR-PSJ y L/T PSJ-PRA respectivamente.
Tabla 9: Resultados Escenario 3 de sobretensiones fase-tierra Ve2 y Vet
Tabla 10: Resultados Escenario 3 de sobretensiones fase-fase Vp2 y Vpt
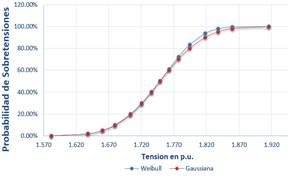
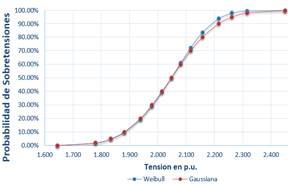
Para el escenario 3, los resultados de la distribución Gaussiana y de Weibull están representados en la Figura 15 y Figura 16.
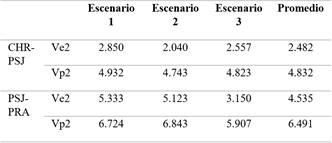
Finalmente, al obtener los valores de sobretensiones Ve2 y Vp2 aplicando las distribuciones estadísticas indicadas, y al ser evaluadas mediante su función completaría, se calcula la diferencia entre los resultados arrojados por la distribución Gaussiana y Weibull modificada mostrados en la Tabla 11. Donde, la variación viene dada en porcentaje y toma como referencia la distribución Gaussiana.
Tabla 11: Resultados de variación de sobretensiones
Al analizar la variación promedio de los voltajes Ve2 y Vp2 de los tres escenarios en las líneas de trasmisión CHR-PSJ y L/T PSJ-PRA, se evidencia que la diferencia es mayor para voltajes de fase-fase.
CONCLUSIONES
Se evidencia que la diferencia que existe entre ambas distribuciones es mínima. La dispersión de datos es menor a 3% en ambos casos, por lo tanto, ambas distribuciones son aplicables para un análisis estadístico de sobretensiones si se consideran magnitudes de voltaje con igual probabilidad de aparecer en el sistema, siendo recomendable por la IEC 60071-2 un 98% de probabilidad.
Las estrategias analizadas en este documento para la reducción de la amplitud de sobretensiones por energización contribuyen a amortiguar la elevación de tensión entre un 35.00 a 40.00 % con respecto al escenario 1. Siendo la mejor opción para controlar el pico de sobretensiones la utilización de resistencias de pre inserción, por otro lado, los bancos de reactores controlan de mejor manera las sobretensiones temporales después de la energización.
Las sobretensiones más elevadas se dieron en el escenario 1 de energización sin control de voltaje con una tensión de 2.688 p.u. con distribución Gaussiana y 2.635 p.u. con distribución Weibull. Estos resultados comprueban la necesidad de controles de voltaje antes de la energización y definen a la distribución de Weibull ligeramente más conservadora que la distribución Gaussiana.