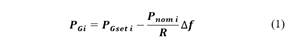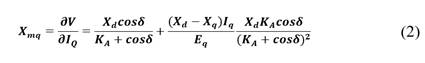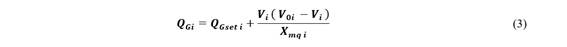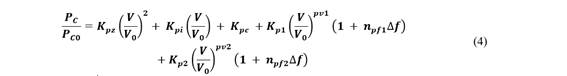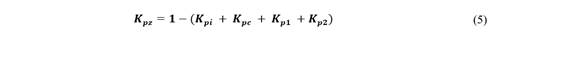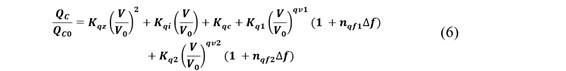INTRODUCCIÓN
Los Sistemas Eléctricos de Potencia (SEP) están formados por una gran variedad de elementos interconectados, desde fuentes de energías renovables no convencionales hasta redes inteligentes, y se caracterizan por tener una alta complejidad, lo que ha llevado al desarrollo de metodologías computacionales en ordenadores de gran capacidad y velocidad para analizar el comportamiento de estos sistemas. Para operar el SEP bajo condiciones de confiabilidad y seguridad adecuadas es imprescindible realizar análisis de estabilidad y de seguridad que determinen vulnerabilidades en el sistema; los principales tipos de análisis son de estabilidad dinámica y de estabilidad estática, siendo este último tipo el objeto de estudio del presente trabajo.
El estudio de estabilidad estática determina las condiciones del sistema en estado estacionario después de una perturbación, buscando un nuevo punto de equilibrio que será una aproximación al punto de estado estable obtenido de un análisis dinámico, para luego verificar que los valores nominales de los equipos o restricciones de voltaje o cualquier otra magnitud no hayan sido violados [1]. Un estudio estático parte de la suposición de que el sistema permanece estable después de la respuesta transitoria, utilizando modelos matemáticos que emulen el efecto de los sistemas de control de los diferentes elementos del SEP, principalmente, regulador de velocidad y regulador automático de voltaje (AVR) [2]. La herramienta fundamental para el análisis de estabilidad estática es el estudio de flujos de potencia.
Los estudios tradicionales de flujos de potencia determinan el punto de equilibrio estable del SEP posterior una perturbación y es un problema que se ha estudiado desde mediados de los años 50 [3], y se sigue estudiando actualmente [4], [5], [6]. Generalmente, los estudios convencionales de flujos de potencia han sido resueltos asumiendo que [7]:
La frecuencia del sistema permanece constante.
El balance generación - carga es regulado por un generador ideal, llamado Slack.
Se consideran nodos PV de generación que suponen un AVR con una ganancia de regulación muy grande, tal que estando dentro de los límites de potencia reactiva es capaz de mantener constante el voltaje en terminales [8].
La dependencia de la carga con el voltaje y frecuencia del sistema es despreciada.
No se considera la acción del control primario del sistema.
Debido a tales consideraciones, un estudio convencional de flujos de potencia es adecuado para el análisis de una condición operativa en que la variación de la frecuencia y el voltaje permanece dentro de rangos limitados; sin embargo, cuando existe una variación importante en el balance generación - carga resulta poco aplicable. Se ha propuesto varias formulaciones alternativas como: el flujo de potencia dinámico [9], [10], [11], y el Flujo de Potencia Inercial (FPI) [7], [5], [12], este último consiste en la modificación de las ecuaciones de balance de potencia, así como del método iterativo de Newton Raphson (modificación al cálculo de la matriz Jacobiana), mediante la inclusión de las ecuaciones estáticas simplificadas que representan la acción de control de los reguladores automáticos de voltaje y de velocidad de los generadores; así como, la inclusión de las expresiones algebraicas que representan la dependencia de la carga con la frecuencia y el voltaje. Esta formulación elimina el concepto de la barra Slack, empleando lo que se conoce como “Slack distribuido”.
En el presente trabajo se presenta la implementación de un algoritmo de flujos de potencia inercial que permite determinar la frecuencia del sistema, el voltaje en las barras y los flujos de potencia por elementos de la red luego de una pérdida repentina de generación carga y/o salida de líneas de transmisión, considerando la acción de los sistemas de control de los generadores y la dependencia de la carga con la frecuencia y el voltaje. El algoritmo es implementado en lenguaje Python, para ser usado a nivel académico y de investigación. En la Sección 2 se presenta la modelación matemática de los elementos del SEP, para en la Sección 3 presentar la formulación matemática del algoritmo de flujos de potencia inercial. La aplicación y resultados de la herramienta desarrollada se presentan en la Sección 4, y finalmente, en la Sección 5 se presentan las conclusiones y recomendaciones del trabajo.
MODELACIÓN DE LOS ELEMENTOS DEL SEP
Para el cálculo de flujos de potencia es necesario definir los modelos matemáticos de los elementos que componen el SEP, de forma que representen fielmente su comportamiento ante diferentes condiciones operativas.
Modelo Estático de los Sistemas de Control del Generador
Todo generador sincrónico está equipado, principalmente, por dos mecanismos de control: el regulador automático de voltaje (AVR) y el regulador de velocidad (Gobernador) [13].
El regulador de velocidad se encarga de realizar la Regulación Primaria de Frecuencia (RPF) en forma automática, modificando la potencia de generación de las unidades en operación. El error de la frecuencia del sistema, en estado estable, depende del efecto combinado del estatismo permanente de los reguladores de velocidad y la sensibilidad de la carga frente a variaciones de frecuencia [14]. Al analizar el comportamiento cuasi estacionario del regulador de velocidad y, suponiendo que la potencia generada se ajusta constantemente a través de pequeños cambios en el valor de referencia, éste puede representarse mediante una sucesión de estados estables, la variación de la potencia generada en el nodo i, ante un cambio de potencia de demanda y en función de la variación de frecuencia viene dada por:
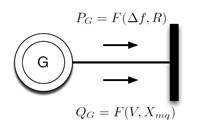
Donde: P 𝑮𝒊 es la potencia total de generación del generador conectado al nodo 𝒊; 𝑷 𝑮𝒔𝒆𝒕 𝒊 es la potencia de generación de la máquina predisturbio; 𝑹 es el estatismo permanente del generador, y ∆𝒇 la variación de la frecuencia en estado estable ante cambios en la demanda o perturbaciones del sistema.
Con respecto al AVR, en el mercado existen diversos diagramas de bloques muy complejos y con un gran número de funciones de transferencia, mismos que son aptos para estudios de estabilidad dinámica. Sin embargo, para el presente trabajo se requiere de un modelo estático del AVR, y se propone utilizar la denominada reactancia equivalente 𝑿 𝒎𝒒 , que matemáticamente se define como la derivada parcial entre el voltaje en los terminales y la corriente 𝑰 𝑸 del generador [15]:
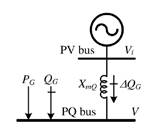
Donde: 𝑿 𝒅 y 𝑿 𝒒 son las reactancias sincrónicas de eje directo y de cuadratura, 𝑬 𝒒 es el voltaje sobre el eje de cuadratura; 𝑲 𝑨 es la ganancia de lazo abierto del AVR; 𝑰 𝑸 es la corriente de eje directo y 𝜹 es el ángulo de carga de la máquina. Esta reactancia, como se observa en la Fig. 1, se puede interpretar físicamente como la pendiente que existe entre el voltaje de la máquina frente a los fasores de corrientes activa y reactiva, cuyo efecto repercute directamente sobre la generación de potencia reactiva, lo cual permite introducir la sensibilidad entre la potencia reactiva generada y el voltaje en terminales, quedando la generación de potencia reactiva expresada como [15]:
Donde: 𝑸 𝑮𝒊 es la potencia de generación reactiva total inyectada al nodo 𝒊; 𝑸 𝑮𝒔𝒆𝒕 𝒊 es la potencia de generación reactiva predisturbio; 𝑽 𝟎𝒊 es el voltaje predisturbio en el nodo 𝒊 y 𝑽 𝒊 es la magnitud de voltaje del nodo 𝒊. En la Fig. 1 se presenta el modelo usado en el FPI luego de una contingencia, donde las barras PV se cambian a barras PQ con la potencia activa y reactiva generada considerando el efecto del regulador de velocidad (estatismo), y se incluye una nueva barra ficticia PV, con el voltaje especificado igual al voltaje especificado inicial del generador, esta barra PV se conecta a través de la reactancia 𝑿 𝒎𝒒 .
Finalmente, se obtiene un modelo alternativo de la máquina sincrónica en el cual la potencia activa generada es función de la desviación de la frecuencia del sistema y el estatismo, y la potencia reactiva generada es función del voltaje en terminales y de la reactancia equivalente 𝑿 𝒎𝒒 , como se muestra en la Fig. 2.
Modelación de la Carga
En el presente trabajo se modela la carga a partir de la sumatoria entre el modelo ZIP y dos modelos exponenciales dependientes de la frecuencia; la finalidad es contar con un modelo flexible y a la vez susceptible a cambios de potencia debido a variaciones en el perfil del voltaje o variaciones de frecuencia del sistema; este modelo permite que se puedan tener varios tipos o características de carga conectadas a una misma barra. De esta manera, la potencia activa de la carga está dada por [16]:
Sujeto a:
Y la potencia reactiva de la carga se calcula como:
Sujeto a:
Donde: 𝑲 𝒑𝒛 y 𝑲 𝒒𝒛 son porcentajes de potencia activa y reactiva de impedancia constante; 𝑲 𝒑𝒊 y 𝑲 𝒒𝒊 son porcentajes de potencia activa y reactiva de corriente constante; 𝑲 𝒑𝒄 y 𝑲 𝒒?? son porcentajes de potencia activa y reactiva de potencia constante; 𝑲 𝒑𝟏 , 𝑲 𝒑𝟐 , 𝑲 𝒒𝟏 y 𝑲 𝒒𝟐 son porcentajes de carga activa y reactiva con característica exponencial dependiente del voltaje; 𝒑𝒗𝟏, 𝒑𝒗𝟐, 𝒒𝒗𝟏 y 𝒒??𝟐 son sensitividades de la carga activa y reactiva con respecto a cambios de voltaje del modelo exponencial; y 𝒏 𝒑𝒇𝟏 , 𝒏 𝒑𝒇𝟐 , 𝒏 𝒒𝒇𝟏 y 𝒏 𝒒𝒇𝟐 son parámetros de sensitividad de la carga activa y reactiva por cambios en la frecuencia.
ORMULACIÓN MATEMÁTICA DEL FLUJO DE POTENCIA INERCIAL
Considere que el SEP está representado por las siguientes ecuaciones de balance de potencia [4]:
Para 𝒊=𝟏, 𝟐, …, 𝒏 barras; donde: ∆ 𝑷 𝒊 , ∆ 𝑸 𝒊 son el desbalance de potencia activa y reactiva del sistema el nodo 𝒊; 𝑷 𝑮𝒊 , 𝑸 𝑮𝒊 son las potencias activa y reactiva generadas en el nodo 𝒊 (ecuaciones 1 y 3); 𝑷 𝑪𝒊 , 𝑸 𝑪𝒊 son las potencias activa y reactiva consumidas por la carga en el nodo 𝒊 (ecuaciones 4 y 6); 𝑷 𝒊 𝒄𝒂𝒍 , 𝑸 𝒊 𝒄𝒂𝒍 son las potencias activa y reactiva inyectadas al nodo 𝒊. Cabe indicar que las nuevas ecuaciones de balance de potencia son funciones dependientes del voltaje nodal 𝑽 𝒊 , del ángulo nodal 𝜽 𝒊 y de la desviación de frecuencia del sistema ∆𝒇:
Aplicando el método de Newton - Raphson, su formulación matricial se expresa como:
Los términos de ∆𝑷 y ∆𝑸, son calculados mediante las ecuaciones 8 y 9 respectivamente, para todas las barras del sistema. Las submatrices jacobianas H y K, de orden (𝒏, 𝒏−𝟏) se construyen para todas las barras, descartando la columna de la referencia angular. Por otro lado, las submatrices N y L están construidas para todas las barras 𝒏 del sistema. Las expresiones empleadas para el cálculo de los elementos de las submatrices H y K, así como, para los elementos fuera de la diagonal de las submatrices N y L, son iguales a las empleadas en el cálculo de flujos de potencia convencional [5]. Sin embargo, para modelar el efecto del AVR en las barras con generador se debe añadir el siguiente término al elemento diagonal de la submatriz L correspondiente al terminal del generador 𝒊 [4]:
Las submatrices F y G de la matriz jacobiana son vectores columna de orden 𝒏, correspondientes a las derivadas parciales de las ecuaciones de balance de potencia 8 y 9 con respecto a la variación de frecuencia. En esta formulación específica, la mayoría de los elementos de estas submatrices son cero cuando no existe una fuente de generación; sin embargo, tomando en cuenta las expresiones de la modelación de la carga, cada elemento de F y G se calcula mediante las siguientes expresiones, para 𝒊=𝟏, 𝟐, …, 𝒏:
Finalmente, el sistema de ecuaciones algebraicas linealizadas, considerando un sistema de "𝒏" barras, en el cual la barra Slack del método convencional (barra "𝒏") se toma únicamente como referencia angular, queda expresado en forma matricial tal como se muestra en la ecuación (17) [5]:
Las magnitudes de tensión en por unidad 𝑽 𝒊 , los ángulos 𝜽 𝒊 , y la desviación de la frecuencia del sistema ∆𝒇 se corrigen iterativamente de acuerdo con la ecuación 18, para cada iteración 𝒌, hasta alcanzar una tolerancia específica, obteniendo como resultado el nuevo punto de equilibrio posdisturbio.
Una vez determinadas las variables de estado del sistema, se pueden calcular las pérdidas de potencia en la red, así como los flujos de potencia a través de los elementos del sistema.
APLICACIÓN Y RESULTADOS
La formulación matemática presentada ha sido implementada en un módulo computacional, desarrollado en lenguaje Python, en el Anexo I se presenta el diagrama de flujo de su funcionamiento. Posteriormente, dicho módulo es aplicado al sistema de prueba IEEE New England de 39 barras y 10 generadores, en donde, partiendo de una condición inicial obtenida mediante un flujo de potencia convencional, se aplica una contingencia de salida de generación o de carga, y se determina el nuevo punto de equilibrio poscontingencia, mediante el FPI.
Caso de Estudio: Salida de Generación
La contingencia consiste en la “salida intempestiva del generador 1, conectado a la barra 30”. En las Tablas I y II se observan la condición inicial del sistema y los resultados del punto de equilibro posdisturbio, obtenidos mediante el FPI y simulación en el dominio del tiempo usando Power Factory de DIgSILENT, con un tiempo total de simulación de 20 segundos, en que se alcanza el nuevo punto de equilibro estable.
Tabla 1: Potencia Activa Generada en Condición Inicial y Nuevo Punto de Equilibrio - Salida de Generación
| Elemento | Condición inicial [MW] | FPI [MW] | Power Factory [MW] | Error Relativo [%] |
| Gen 1 | 250 | 0 | 0 | 0.000 |
| Gen 2 | 520.81 | 548.18 | 548.34 | 0.028 |
| Gen 3 | 650 | 677.37 | 677.44 | 0.010 |
| Gen 4 | 632 | 659.37 | 659.49 | 0.018 |
| Gen 5 | 508 | 535.37 | 535.43 | 0.010 |
| Gen 6 | 650 | 677.37 | 677.46 | 0.013 |
| Gen 7 | 560 | 587.37 | 587.55 | 0.030 |
| Gen 8 | 540 | 567.37 | 567.56 | 0.032 |
| Gen 9 | 830 | 859.97 | 864.53 | 0.528 |
| Gen 10 | 1000 | 1000 | 1000.67 | 0.067 |
| Total | 6140.81 | 6112.37 | 6118.46 |
Respecto de la potencia activa generada, los resultados muestran que todos los generadores contribuyen a solventar el déficit de generación, según el modelo de barra Slack Distribuida, lo que se asemeja a la respuesta real del SEP. Se aprecia también que la modelación estática del regulador de velocidad permite alcanzar una potencia activa de generación similar a la obtenida mediante la simulación en el dominio del tiempo, presentando errores menores al 1%.
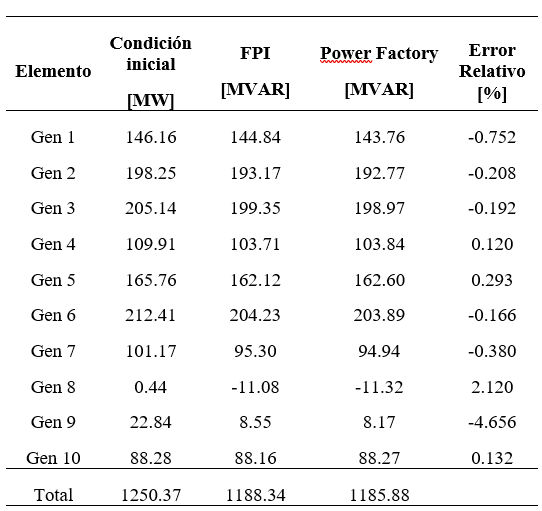
Tabla 2: Potencia Reactiva Generada en Condición Inicial y Nuevo Punto de Equilibrio - Salida de Generación
| Elemento | Condición inicial [MVAR] | FPI [MVAR] | Power Factory [MVAR] | Error Relativo [%] |
| Gen 1 | 146.16 | 0.00 | 0.00 | 0,000 |
| Gen 2 | 198.25 | 230.54 | 230.31 | -0.102 |
| Gen 3 | 205.14 | 238.91 | 238.84 | -0.031 |
| Gen 4 | 109.91 | 133.09 | 133.48 | 0.296 |
| Gen 5 | 165.76 | 177.99 | 178.22 | 0.125 |
| Gen 6 | 212.41 | 240.47 | 240.82 | 0.144 |
| Gen 7 | 101.17 | 119.43 | 119.95 | 0.428 |
| Gen 8 | 0.44 | 64.97 | 64.61 | -0.566 |
| Gen 9 | 22.84 | 50.24 | 51.08 | 1.636 |
| Gen 10 | 88.28 | 96.72 | 99.60 | 2.886 |
| Total | 1250.37 | 1352.39 | 1356.90 |
Respecto a la potencia reactiva generada, la modelación estática del AVR permite obtener una respuesta similar a la obtenida mediante simulación en el dominio del tiempo, provocando que cada generador aporte los reactivos necesarios para tratar de mantener el perfil de voltaje. Los errores de potencia reactiva generada, en su mayoría, se mantienen por debajo del 1% a excepción de los generadores 9 y 10 (barras 38 y 39) donde es error es menor al 3%. Se debe mencionar que las diferencias entre potencias reactivas de generación obtenidas mediante la herramienta desarrollada y Power Factory son menores a 3 MVAR y representan un mínimo porcentaje respecto de la potencia reactiva total del sistema (1357 MVAR).
Los errores están relacionados con la modelación de la dependencia de la carga con el voltaje y la frecuencia, principalmente. Power Factory implementa un modelo ZIP, y por ende, existirán diferencias respecto de la propuesta de modelación de la carga del presente trabajo. Otras fuentes de error es la modelación de los límites de generación de potencia reactiva, el FPI implementa límites fijos mientras que Power Factory modela las curvas de capacidad de los generadores y los límites definidos por limitadores de sub y sobre excitación.
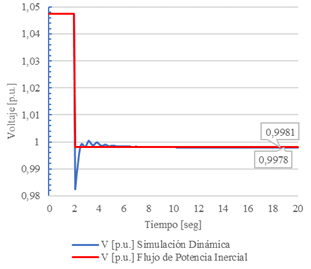
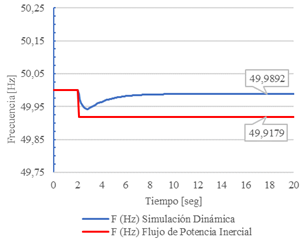
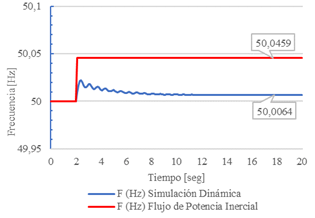
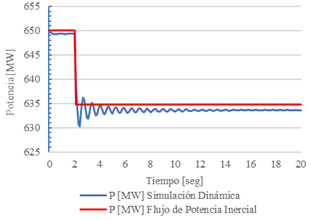
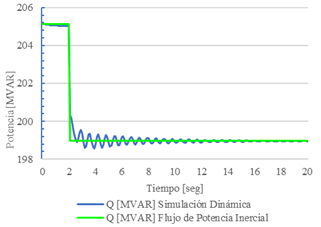
Adicionalmente, se presenta una comparación entre la magnitud del voltaje y la frecuencia de la barra 30, así como la potencia activa de generación de la barra 31, obtenidas mediante el FPI y simulación en el dominio del tiempo. Los resultados se muestran en las Figs 3, 4 y 5.
En las Figs. 3 y 4 se aprecia como ambos métodos encuentran un nuevo punto de equilibrio estable en voltaje y frecuencia con una diferencia mínima. Cuando se considera la frecuencia, el error relativo es de 0.143%, mientras que cuando se considera el voltaje, el error relativo 0.03%. En este caso de estudio, el punto de equilibro alcanzado con el FPI es prácticamente igual al obtenido mediante simulación en el dominio del tiempo.
Finalmente, en la Fig. 5 se aprecia como la modelación del regulador de velocidad en el FPI permite alcanzar un nivel de generación muy cercano al obtenido con simulación en el dominio del tiempo.
Caso de Estudio: Pérdida de Carga
En este caso la contingencia consiste en la “salida intempestiva de la carga conectada a la barra 26”. Los resultados se presentan en las Tablas III y IV donde se han hecho similares consideraciones que el caso de estudio anterior. Todos los generadores aportan con potencia activa y reactiva para contener las variaciones de frecuencia y voltaje producto de la contingencia.
Tabla 3: Potencia Activa Generada en Condición Inicial y Nuevo Punto de Equilibrio - Pérdida de Carga
Al igual que en el caso anterior, se observa que la modelación propuesta de los sistemas de control (regulador de velocidad y AVR) permite alcanzar un punto de equilibrio poscontigencia similar al obtenido con simulación en el dominio del tiempo. En el caso de la potencia activa generada, los errores relativos no superan el 1%.
Tabla 4: Potencia Reactiva Generada en Condición Inicial y Nuevo Punto de Equilibrio - Pérdida de Carga
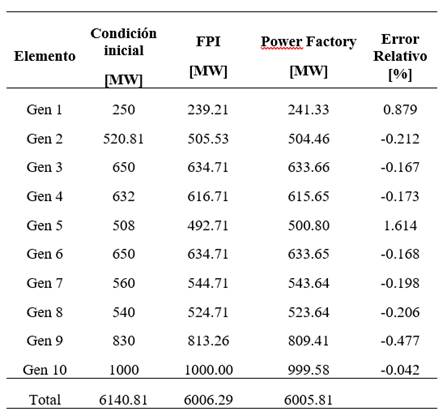
Respecto de la potencia reactiva generada, en la mayoría de los casos, el error relativo se mantiene por debajo del 3%, a excepción de la barra 38 (Gen 9) que llega al 5%. La causa está relacionada con la modelación de la carga y los límites de generación de potencia reactiva de los generadores, como se explicó en el caso de estudio anterior.
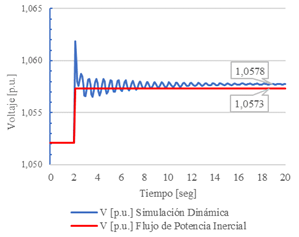
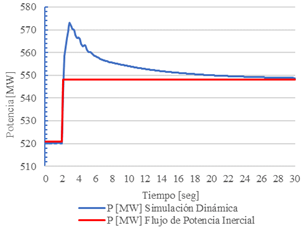
En las Figs. 6 y 7 se presenta la comparación de resultados obtenidos mediante el FPI y la simulación en el dominio del tiempo usando Power Factory, tomando como variables de análisis la magnitud del voltaje y la frecuencia en la barra 26.
En ambos casos, se alcanza un nuevo punto de equilibrio estable, con una diferencia mínima. El error relativo de la frecuencia es de 0,079%, mientras que cuando se analiza la magnitud del voltaje, el error relativo es de 0.05%.
En las Figs. 8 y 9 se muestran las potencias activa y reactiva generadas en la barra 32 (Gen 3), donde se puede apreciar que la modelación estática del AVR como del regulador de velocidad, permiten alcanzar un punto de equilibrio estable similar al obtenido por simulación en el dominio del tiempo.
El pequeño error relativo en las variables de frecuencia, potencias activa y reactiva generadas, así como la tendencia observada en las figuras presentadas en ambos casos de estudio, muestran que los resultados obtenidos mediante el FPI son similares a los obtenidos mediante simulación en el dominio en el tiempo, con lo que se valida su desempeño.
Cabe mencionar que ambos casos (FPI y simulación en el dominio del tiempo) es necesario determinar la condición inicial predisturbio, mediante un flujo de potencia convencional. El FPI presenta menor tiempo de cálculo del nuevo punto de equilibrio poscontingencia respecto del tiempo de simulación en el dominio del tiempo, con resultados similares. Respecto del flujo de potencia convencional, el FPI permite determinar la frecuencia alcanzada luego de una contingencia que modifique el balance generación - carga y una redistribución de los flujos de potencia más realista, considerando la respuesta real de los generadores debido a sus sistemas de control.
CONCLUSIONES Y RECOMENDACIONES
El análisis en estado estable del regulador de velocidad y la consideración de la reactancia equivalente 𝑿 𝒎𝒒 que emula la acción del AVR del generador, permiten introducir las sensibilidad de potencia activa y reactiva de generación en las ecuaciones de balance de potencia nodal, convirtiéndolas en ecuaciones dependientes de los cambios de voltaje y de frecuencia; esto permite la inclusión de derivadas parciales que modifican la matriz jacobiana para el flujo de potencia inercial.
El módulo de software desarrollado considera parámetros técnicos reales como el estatismo de estado estable del regulador de velocidad y la ganancia de lazo abierto del AVR, que caracterizan a los sistemas de control de los generadores. Para la aplicación de la herramienta desarrollada a SEP reales de gran dimensión, suele ser un reto obtener dicha información.
Con el flujo de potencia inercial se obtienen resultados cercanos a la realidad operativa y permite apreciar las estrechas relaciones que existen entre la potencia activa y la frecuencia, así como entre la potencia reactiva y los voltajes nodales, pudiendo convertirse en una herramienta académica para el análisis de la operación del SEP. En ese sentido, los resultados obtenidos muestran que el flujo de potencia inercial consigue una redistribución de los flujos de potencia, implementado concepto de barra Slack distribuida, que permite que todos los generadores aporten a la regulación de la frecuencia del sistema, según la acción de su regulador de velocidad. Los resultados obtenidos se asemejan a la operación real del SEP.
Finalmente, como trabajos futuros se propone la aplicación de la herramienta desarrollada a SEP reales, como el Sistema Nacional Interconectado Ecuatoriano, y su uso en estudios de determinación de reservas de potencia, diseño de esquemas de alivio de carga, así como la inclusión de nuevas tecnologías de generación.