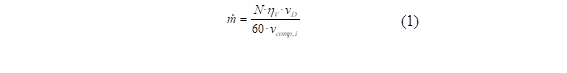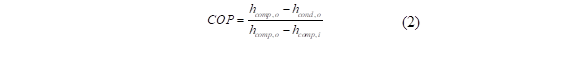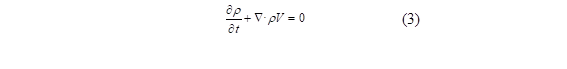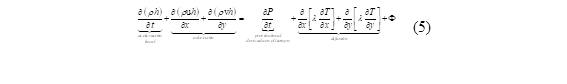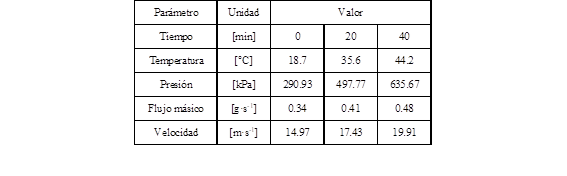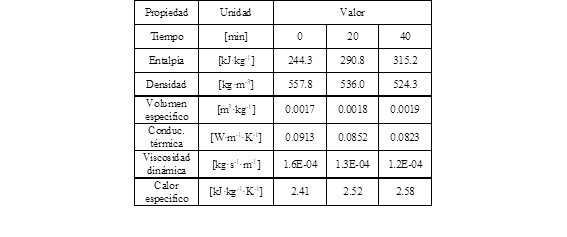INTRODUCCIÓN

El calentamiento solar de agua se considera una herramienta utilizada para la reducción de consumo de energía convencional. Para el 2020, en Ecuador el consumo final de energía del sector residencial es del 37.4 % y la cuarta parte de este consumo es empleado en el calentamiento de agua [1]. El mayor consumo energético para calentamiento de agua en el sector residencial es proporcionado por calefones, que consumen gas licuado de petróleo (GLP), con un 80.6 %. Los calentadores de agua de resistencia eléctrica son utilizados en un 11.2 % y apenas el 8.2 % de hogares han implementado algún calentador de agua aprovechando la energía térmica del sol [2].

La bomba de calor absorbe calor de un entorno a temperatura media y lo utiliza para calentar otro medio a diferente temperatura. Una tecnología innovadora y efectiva es implementar un colector solar a una bomba de calor. Un sistema de bomba de calor asistido por energía solar de expansión directa (DX-SAHP, por sus siglas en inglés) utiliza el colector solar como evaporador en una sola unidad, para absorber calor por energía solar o convección del ambiente y permitir que el refrigerante cambie de fase [3]. Estos sistemas son hasta 30 % más eficiente que un calentador eléctrico convencional y las emisiones de CO2 se reducen en 19 %. [4]. Además, como alternativa para el reemplazo de refrigerantes hidrofluorocarbonos (HFC), se está promoviendo el uso de hidrocarburos como refrigerantes naturales, aunque en su mayor parte, su implementación ha sido en el sector residencial [5]. A continuación, se presentan investigaciones previas, analizando los dispositivos de expansión utilizados.

Una revisión de los avances tecnológicos de sistemas DX-SAHP fue presentada por Badiei et al. [6]. El desarrollo sustentable ha conllevado que se deje de utilizar refrigerante R12, siendo R134a el refrigerante con mayor y más amplio campo de aplicaciones. El coeficiente de rendimiento (COP, por sus siglas en inglés) puede alcanzar valores de 9 y en promedio de 6, para sistemas DX-SAHP. De esta revisión se ha concluido que, la mayor cantidad de investigaciones han sido desarrolladas con un análisis numérico, siendo pocos los trabajos desarrollados de manera experimental, y teniendo escasos trabajos que han complementado los dos métodos. Además, el estudio afirma que, utilizar una válvula de expansión electrónica mejora el control del flujo másico de refrigerante, comparado ante un dispositivo termostático. Este control generó reducción en las pérdidas de calor durante el estrangulamiento y conlleva a incrementar el rendimiento del sistema.

El rendimiento experimental de un sistema DX-SAHP con CO₂ fue analizado por Duarte et al. [7]. La válvula de expansión utilizada fue de tipo aguja, diseñada para trabajar únicamente con CO₂ y un orificio de salida con un área de 1.6 mm². Se desarrollaron 88 experimentos y se utilizó una cámara termográfica, donde el COP disminuyó 45.8 % cuando el agua varió su temperatura de entrada entre 15 a 35 °C. El valor del COP también depende directamente de la radiación solar incidente, el COP se incrementó un 30 % cuando la radiación solar aumento de 30.17 a 876.9 W·m^-2.

Un sistema DX-SAHP depende directamente de las condiciones climáticas, siendo necesario desarrollar alternativas para su funcionamiento en condiciones desfavorables. Li et al. [8] estudiaron el rendimiento de una bomba de calor con un calentador auxiliar de agua bajo diferentes valores de temperatura ambiente. El propósito fue mantener el rendimiento del sistema aún a bajas temperaturas añadiendo a la bomba de calor otro sistema de almacenamiento de energía. El estudio se incluyó la variación del porcentaje de apertura de la válvula de expansión, llegando a determinar un rango de apertura óptimo entre 50 a 70 %. Esta investigación ha propuesto un novedoso sistema para evitar el deterioro de un sistema DX-SAHP cuando las condiciones climatológicas no son favorables en el rendimiento.

El estudio numérico y la validación experimental de un sistema DX-SAHP para calentamiento de entornos bajo cero fueron realizados por Huang et al. [9]. Un modelo dinámico fue utilizado para la obtención de resultados simulados con una desviación cuadrática de 6 %. Para validar el modelo numérico, fueron obtenidos resultados experimentales en un prototipo que constó con una válvula de expansión termostática, obteniendo una desviación cuadrática de 4.01 y 2.78 % para la capacidad calorífica y el consumo energético, respectivamente. El sistema fue analizado considerando una temperatura de -1 °C, 70 % de humedad relativa y radiación solar de 0 W·m^-2, llegando a alcanzar un COP de 1.89. Cuando la radiación solar subió a 100 W·m^-2, el COP llegó a 1.97 y la capacidad calorífica a 1 082 W.

Las investigaciones concernientes al análisis numérico están enfocadas al modelamiento matemático, así como simulación computacional del sistema DX-SAHP, en conjunto. Loska et al. [10] realizaron un modelamiento de dinámica de fluidos computacional (CFD, por sus siglas en inglés) del flujo de R410A a través de una válvula de expansión utilizando modelos de equilibrio y relajación modificada. El análisis fue realizado tomando las medidas del flujo másico y la presión del refrigerante en el ingreso del dispositivo de expansión. Este dispositivo estuvo completamente abierto y las temperaturas de subenfriamiento mínima y máxima fueron 3.8 a 7.7 K, respectivamente, cuando las presiones estuvieron desde 6.8 a 11.5 bar.

Kong et al. [11] estudiaron un sistema DX-SAHP para calentamiento de agua mediante un modelo de simulación incluyendo todos los componentes para establecer el rendimiento térmico del sistema. Se plantearon ciertas consideraciones en el modelado matemático, como asumir la compresión como un proceso politrópico, la temperatura en toda la superficie del colector solar permanece igual y las presiones son constantes en los intercambiadores de calor. Una válvula de expansión electrónica fue implementada en el sistema para realizar los experimentos, Mientras que, los cálculos realizados permitieron verificar adecuadamente las predicciones con una desviación promedio de 5.5 % entre el valor del COP experimental y el calculado. El COP alcanzó valores por encima de 2.75 al calentar un volumen de agua de 200 L desde 5 a 45 °C con temperatura ambiente casi constante de 1 °C, considerando una radiación solar de 100 a 350 W·m^-2

Mediante un modelo basado en redes neuronales, Kong et al. [13] predijeron el flujo másico de R290 en un sistema DX-SAHP. El sistema estuvo conformado por un colector de placa descubierta, un compresor de velocidad variable, un condensador en tubería de cobre inmerso y una válvula de expansión electrónica. Se utilizó el medidor de flujo Coriolis para la obtención de medidas experimentales. Mientras que, para el modelo de redes neuronales, se definieron 5 variables de entrada, temperatura ambiente, radiación solar, área de flujo de la válvula de expansión, frecuencia del compresor y temperatura del agua. El modelo tuvo una exactitud del 97 % con respecto a los resultados experimentales, con un máximo error de 10 %. La temperatura ambiente es el parámetro de mayor influencia en el flujo másico de refrigerante, al utilizar las otras variables con valores definidos, el flujo másico varió de 4.59 a 11.63 kg·h^-1 cuando la temperatura ambiente subió de 0 a 10 °C.

Wang et al. [12] estudiaron la influencia del subenfriamiento en el rendimiento de un sistema DX-SAHP. Mediante un modelo matemático dinámico, los autores tomaron una configuración previamente desarrollada e implementaron una válvula de expansión con un receptor de líquido. Los resultados indicaron que, la capacidad térmica de calentamiento depende de la variación del grado de subenfriamiento. El COP máximo del sistema llegó fue 14.35 % superior cuando la evaporación permaneció a 4 K, estando en valores elevados al controlar esta temperatura entre 2 a 5 K.

El error admisible para la validación de los resultados simulados con respecto a los resultados experimentales puede ser analizado en función a investigaciones previas. Weian et al. [4] llegaron a estimar un error relativo de 1.3 % en el COP, al relacionar los parámetros medidos con los valores calculados mediante fórmulas. Por otra parte, Kong et al. [14] desarrollaron un modelo para predecir resultados en función de los parámetros operacionales con un error relativo máximo del 10 %. Además, Knabben et al. [15] investigaron la utilidad de válvulas de expansión electrónicas en sistemas de refrigeración domésticos. Un modelamiento matemático para estimar la significancia de la cantidad de refrigerante en el COP del sistema fue utilizado en el análisis. Se demostró que, una válvula de expansión electrónica consume de 4 a 9 % menos energía que un sistema que utiliza un tubo capilar. El error obtenido entre las mediciones experimentales y los resultados de simulación estuvo dentro del 15 %. Cuando la apertura de la válvula de expansión es menor, así como al reducir la cantidad de refrigerante, el consumo energético del sistema también disminuye.

En esta investigación se ha planteado realizar una simulación numérica en un dispositivo de expansión, para analizar la influencia de los parámetros operacionales. De esta manera, se obtendrá valor de presión instantánea del refrigerante para las condiciones establecidas y así, presentar una comparación con respecto a los valores experimentales. Este documento se encuentra distribuido de la siguiente manera, en Materiales y Métodos se indican los procedimientos realizados para desarrollar el análisis numérico. Los resultados presentan gráficamente los valores obtenidos mediante simulación, así como su descripción. Por último, las Conclusiones muestran el análisis de la información y resultados que se han presentado.

MATERIALES Y MÉTODOS

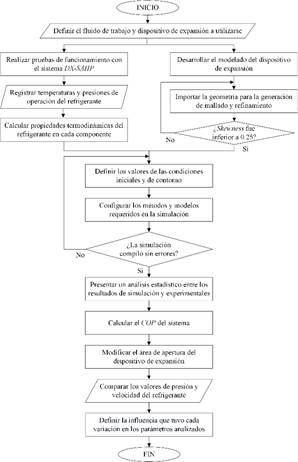
La Fig. 1 presenta las actividades realizadas para desarrollo este trabajo, mediante un diagrama de flujo.

Descripción del Sistema

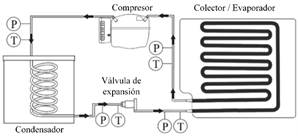
La Fig. 2 presenta el esquema de un sistema DX-SAHP que funciona con un ciclo de refrigeración mediante la compresión de vapor. El colector / evaporador de un sistema DX-SAHP utiliza la energía térmica emitida por el sol y la transfiere al refrigerante para evaporarlo. Este refrigerante sobrecalentado ingresa al compresor para elevar su presión y temperatura, de esta manera, pueda realizar un intercambio de calor con el tanque de almacenamiento de agua. Para finalizar el proceso, el refrigerante en estado de líquido subenfriado ingresa al dispositivo de estrangulamiento para expandirse a entalpía constante e ingresar como líquido a baja temperatura y presión al evaporador [16]. Se utilizó termocuplas (T) y manómetros (P) a la entrada de cada componente para el registro de las mediciones.

El flujo másico instantáneo del refrigerante (ṁ) es obtenido en función de parámetros operacionales, así como mediciones de temperatura y presión a la entrada del compresor. Para Deng y Yu [17], este valor es obtenido mediante:

donde N, η_V y v_D son la velocidad rotacional, la eficiencia volumétrica y el volumen de desplazamiento del compresor, respectivamente. Mientras que, v_{comp, i} es el volumen específico del refrigerante al ingresar en el compresor.

Figura 1: Diagrama de flujo para desarrollar esta investigación 

Figura 2: Esquema del sistema DX-SAHP [17] 

El funcionamiento de estos sistemas considera un ciclo de refrigeración por compresión de vapor, entonces, para el análisis termodinámico, se evalúa su rendimiento mediante el COP. Este valor relaciona la cantidad de unidades de energía térmica que son generadas a partir de las unidades de energía eléctrica requeridas para el funcionamiento del sistema [18]. Weian et al. [19] calcularon este valor utilizando:

donde h es la entalpía del refrigerante, al ingresar y salir del compresor y condensador, respectivamente.

Ecuaciones gobernantes para diseño de fluidos computacional

El análisis numérico fue planteado utilizando el modelo tridimensional utilizando el método de volúmenes finitos. El modelamiento matemático ha considerado al refrigerante R600a como un fluido Newtoniano en estado estacionario. Es importante tener presente la ley de conservación de la masa, además que, la masa es obtenida al multiplicar la densidad (ρ) por su volumen [20]. Al definir un volumen de control para un fluido en movimiento, la conservación de la masa requiere que la rapidez con la que la masa cambia en este volumen sea equivalente a la masa que fluye por la superficie del volumen. Según Scuro et al. [21], la ecuación de la continuidad viene dada por:

donde ∇V representa la divergencia de la velocidad.

La segunda ley de Newton indica que, el total de fuerzas actuantes sobre el fluido se obtiene multiplicando la masa y la aceleración. Un aspecto para considerar es que, se presentan fuerzas sobre el cuerpo, efectos adicionados a las fuerzas superficiales. Para un fluido en estudio bidimensional, la ecuación de momento, considerando las relaciones de esfuerzos, para un fluido compresible, es estimada por Aghagoli y Sorin [22] mediante la siguiente expresión:

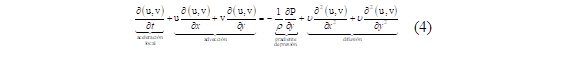donde υ es la viscosidad cinemática. La ecuación 4 también ha sido definida como la ecuación de Navier-Stokes, además, se ha descrito la interpretación física de cada término [23].

Con respecto a la conservación de la energía, siempre se debe realizar el análisis considerando la primera ley de la Termodinámica. El trabajo realizado en un volumen de control es equivalente al producto entre las fuerzas superficiales por la velocidad en una dirección. Además, la energía total del fluido está definida por la sumatoria de energía cinética, potencial gravitacional e interna, también como la entalpía (h), para este caso. La ecuación de conservación de la energía para fluidos compresibles ha sido determinada por Tu et al. [24] como:

donde Φ representa la función de disipación como fuente de energía debido al trabajo de deformación realizado en el fluido, λ y T son la conductividad térmica y temperatura del fluido, respectivamente.

Modelado del dispositivo de expansión

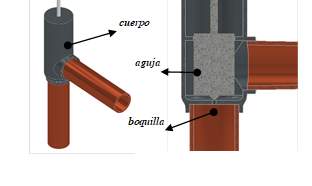
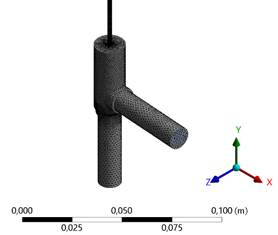
La Fig. 3 muestra el modelado del objeto en análisis, una válvula de expansión electrónica modelo E2V09SSF. Se ha considerado el dispositivo mecánico para el proceso de simulación, omitiendo los dispositivos electrónicos. Como componentes principales, se tiene un cuerpo, una aguja para la calibración, y una boquilla. La válvula produce un proceso de estrangulamiento para regular el flujo de refrigerante previo a la entrada al colector / evaporador, al disminuir la presión y temperatura atomizando el refrigerante [25]. Una válvula de expansión permite regular la apertura para el flujo de manera mecánica y mediante control, respectivamente, obteniendo un mayor rendimiento con la electrónica [26]. El fluido ingresa por la derecha para salir por la parte inferior.

Figura 3: Modelado de la válvula de expansión 

Mallado

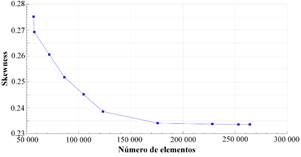
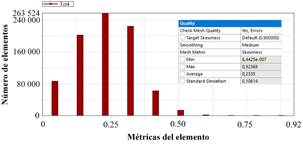
Se utilizaron diferentes métodos para la generación del mallado en el elemento, buscando obtener la mejor calidad. La Fig. 4 muestra la convergencia de malla para obtener un skewness adecuado en función del número de elementos. Una calidad excelente de mallado debe estar dentro de los rangos establecidos, con skewness inferior a 0.25 [27]. Al generar la malla de manera automática, se obtuvo un valor de skewness de 0.2752 para 56 859 elementos. Esta métrica empieza a converger en 260 000 elementos, aproximadamente, con un skewness promedio de 0.2335. La diferencia con respecto a la malla anterior de 175 000 elementos es del 2 %, mientras que la cantidad de elementos se han incrementado en un 48.57 %.

Figura 4: Convergencia de la malla 

La Fig. 5 indica, en detalle, el tipo de mallado generado para el elemento a analizar. El procedimiento para generar la malla fue realizado utilizando métodos, como refinamiento y dimensionamiento, con el que se obtuvieron 263 524 elementos y un total de 50 449 nodos. El tamaño de grano fue definido en 1.2, con un ángulo de 10 °, aplicando tetraedros dominantes. Se ha definido como un sólido a todos los componentes de la válvula, mientras que, al fluido se le ha dado una denominación en este estado.

Figura 5: Mallado de la válvula de expansión 

La Fig. 6 presenta los valores obtenidos para la métrica de calidad de mallado generado, donde el skewness presentó un valor de 0.2335, en promedio. Como el valor de skewness fue menor a 0.25, se afirma que el mallado generado tiene una excelente calidad.

Figura 6: Métrica de calidad del mallado 

Condiciones de contorno

La temperatura, así como la presión de ingreso al dispositivo de expansión se definieron como condiciones de contorno a la entrada y salida. El espesor de pared es de 2 mm, fabricada en cobre, un material conductivo. La Tabla 1 presenta los valores de condiciones iniciales para realizar la simulación.

Las propiedades termodinámicas para los estados, vapor y líquido, del refrigerante fueron evaluadas en función de la presión y temperatura utilizando el software Engineering Equation Solver (EES). La Tabla 2 muestra las propiedades instantáneas del refrigerante al ingreso del dispositivo de expansión, calculadas con la temperatura y presión medidas experimentalmente, en el intervalo de tiempo de 40 minutos para calentar el volumen de agua.

Tabla 1: Valores de condiciones iniciales para el refrigerante 

Tabla 2: Propiedades del refrigerante 

RESULTADOS

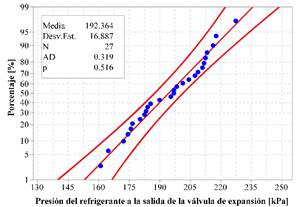
Los valores experimentales fueron obtenidos utilizando un prototipo de sistema DX-SAHP utilizado en las investigaciones de Isaza-Roldán et al. [28] y Quitiaquez et al. [29]. Estos valores fueron validados mediante una prueba de normalidad, con una confianza del 95 %. La Fig. 7 muestra los valores de presión absoluta del refrigerante al salir del dispositivo de expansión obtenidos de forma experimental, donde se evidencia que los valores siguen una normalidad. El valor promedio de presión del refrigerante fue de 192.36 kPa, además, el mayor y menor valor fue de 232.33 y 163.38 kPa, respectivamente.

Figura 7: Normalidad de la presión del refrigerante 

La Fig. 8 relaciona los valores de presión del refrigerante al salir del dispositivo de expansión. En el desarrollo experimental, esta presión fue de 163.38, 190.96 y 232.33 kPa al inicio, en medio y al finalizar el proceso de calentamiento, respectivamente. Mientras que los valores obtenidos mediante simulación presentaron un error de 1.09, 2.38 y 2.52 %, para cada tiempo, respectivamente.

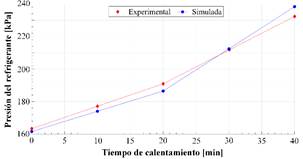
Figura 8: Relación entre la presión del refrigerante al salir del dispositivo de expansión, experimental y simulada 

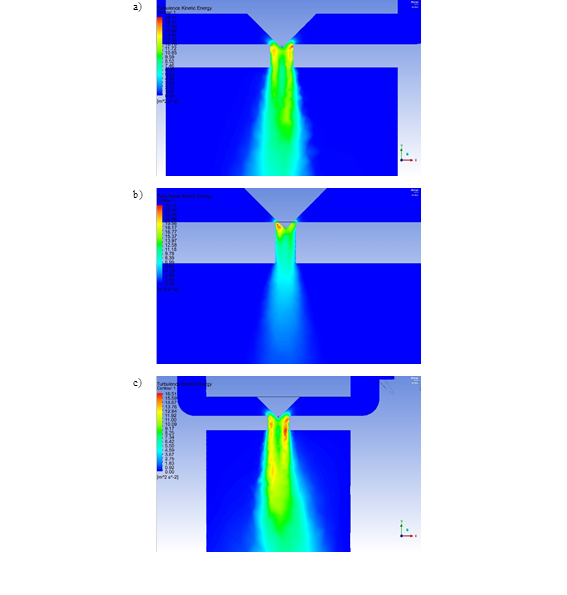
Se pretende analizar cómo interviene la apertura del dispositivo de expansión en la presión del refrigerante. La Fig. 9 presenta la expansión del refrigerante con tres diferentes modelos utilizados, en los que se varió el área de flujo a través de la válvula de expansión. Los valores de presión fueron de 161.61, 164.51 y 152.95 kPa, para áreas de 1, 0.25 y 2.25 mm², respectivamente. Con estos valores, se evidencia que, a medida que se incrementa el área de flujo, es mayor la caída de presión del refrigerante al salir del dispositivo de expansión

La Fig. 10 compara el flujo másico experimental con respecto a los valores obtenidos mediante simulación, considerando una presión inicial de 290.93 kPa. El flujo másico experimental tuvo un valor de 0.3409 g·s^-1, mientras que, mediante simulación, para un área de 1, 0.25 y 2.25 mm², el flujo másico presentó valores de 0.3416, 0.3420 y 0.3410 g·s^-1, respectivamente. Por la ley de continuidad, si se mantiene un flujo, pero se reduce el área, incrementa la velocidad del fluido, entonces, el compresor presenta un menor consumo energético. Los resultados obtenidos son similares a los presentados por Nguyen y Dang [30], afirmando que, un incremento de flujo másico es directamente proporcional al aumento del COP.

La Fig. 11 muestra los vectores de velocidad del refrigerante para las diferentes áreas de flujo analizadas. El vapor de refrigerante es atomizado al fluir a través del área de flujo del dispositivo de expansión, donde alcanza el máximo de su velocidad. Además, es evidente que hay varias regiones donde el refrigerante se acumula y no genera cambios en su velocidad. La velocidad máxima del refrigerante fue inferior en el área de menor apertura, 0.25 mm², teniendo 16.27 m·s^-1. Mientras que, para los casos restantes de estudio, la velocidad del refrigerante alcanzó valores máximos cercanos a 21.61 m·s^-1, aproximadamente.

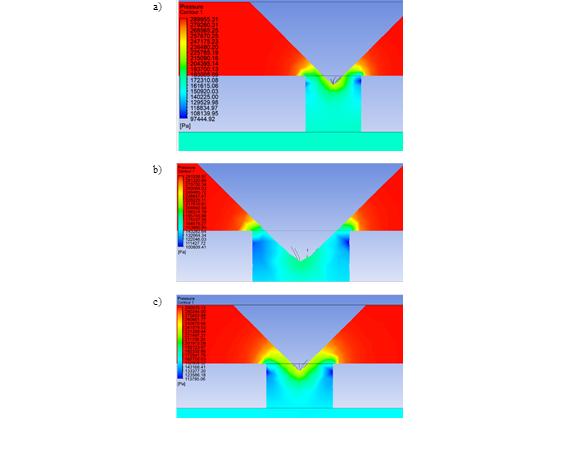
Figura 9: Expansión del refrigerante en la válvula de expansión con diferentes áreas a) 1 mm², b) 0.25 mm², c) 2.25 mm² 

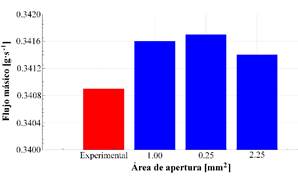
Figura 10: Comparación del flujo másico experimental respecto a los valores obtenidos en simulación variando el área de apertura 

La Fig. 12 muestra los contornos de turbulencia para la energía cinética cuando el refrigerante fluyó por el dispositivo de expansión. Se utilizó un modelo k-epsilon con el método RNG utilizado por la susceptibilidad para recirculaciones internas [23]. La variación de turbulencia está dada por escala de color, desde 0 hasta 25 m²·s^-2. La turbulencia se incrementó al reducirse el área de flujo del dispositivo de expansión. Al utilizar un área de apertura de 1 mm² para la comparación con los resultados experimentales, la turbulencia máxima y promedio fueron de 19.17 y 10.65 m²·s^-2, respectivamente. Cuando el área de apertura fue reducida a 0.5 mm² e incrementada a 2.55 mm², esta turbulencia se aumentó y disminuyó en 31.19 y 13.87 %, respectivamente.

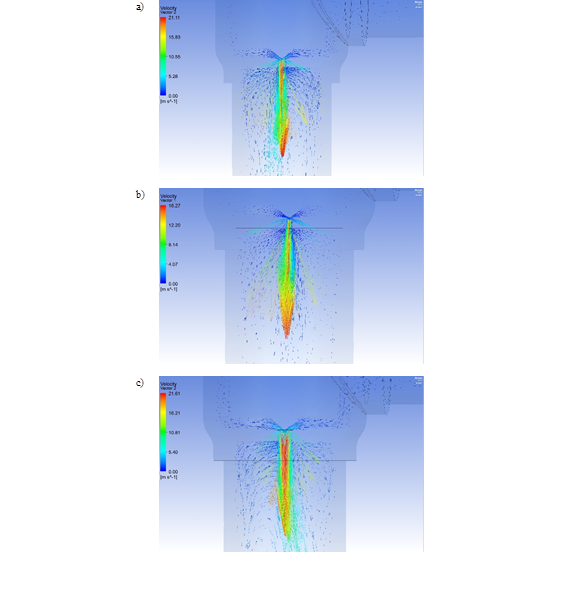
Figura 11: Vectores de velocidad del refrigerante para diferentes áreas a) 1 mm², b) 0.25 mm², c) 2.25 mm² 

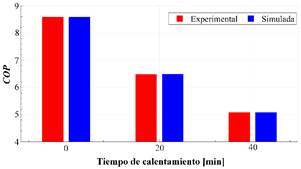
En el análisis termodinámico del sistema con los datos experimentales, el COP alcanzó un valor máximo de 8.59 al iniciar el proceso de calentamiento de agua. También se tuvo un valor de COP mínimo de 5.08, mientras el COP promedio fue 6.48. Los valores obtenidos mediante simulación presentaron un error inferior a 1 % para los períodos de tiempo analizados.

CONCLUSIONES

El rendimiento termodinámico de un sistema DX-SAHP fue evaluado mediante la simulación numérica del proceso de estrangulamiento en el dispositivo de expansión. Del análisis de resultados obtenidos, así como de la comparación con los resultados experimentales, se han obtenido las siguientes conclusiones.

Figura 12: Turbulencia del refrigerante para diferentes áreas a) 1 mm², b) 0.25 mm², c) 2.25 mm² 

Figura 13: Comparación de COP del sistema 

El prototipo de sistema DX-SAHP disponible se utilizó para calentar agua a 45 °C, establecida como agua caliente sanitaria. El refrigerante R600a fue utilizado como fluido de trabajo, con una carga de 100 g, mientras que el volumen de agua calentado fue de 10 litros. El tiempo de calentamiento varió, teniendo en promedio una duración entre 40 a 50 minutos. Los experimentos se realizaron bajo diferentes condiciones climáticas, tomando parámetros operativos de presión y temperatura cada 5 minutos. Estos datos fueron considerados para calcular las propiedades termodinámicas del fluido de trabajo.

El modelado de la válvula de expansión consideró las dimensiones del modelo E2V09SSF, utilizando una aguja para la regulación. El proceso de simulación fue desarrollado en este modelo con una malla generada de calidad 0.2335 de skewness, obteniendo 263 524 elementos y 50 449 nodos. Las condiciones de contorno definidas fueron la presión y temperatura del fluido al ingreso del dispositivo de expansión, con valores promedio de 35.6 °C y 497.77 kPa. Se utilizó el módulo Fluent del software ANSYS, con un modelo de energía y k-epsilon RNG para turbulencia, además, la velocidad del refrigerante entre 14.973 a 19.911 m·s^-1. La radiación solar incidente tiene influencia en la temperatura y presión del refrigerante.

Los resultados experimentales fueron validados mediante un análisis de varianza mediante p valor con una confianza del 95 % para la temperatura del refrigerante al salir del dispositivo de expansión. Se generó un diseño factorial completo de 27 experimentos para los tres factores definidos como condiciones de contorno, temperatura, presión y flujo másico del refrigerante al ingreso de la válvula de expansión, cada uno con 3 niveles. Los valores experimentales de presión de salida siguieron una distribución normal, por lo que se afirmó su validez y fueron utilizados para el análisis numérico. Los valores de presión obtenidos mediante simulación, para un tiempo de calentamiento en 0, 20 y 40 minutos, fueron de 161.61, 186.50 y 238.33 kPa. Los errores absoluto y relativo de la presión experimental y simulada fueron de 4.07 kPa y 2 %, respectivamente. Se puede afirmar que, según aumenta el subenfriamiento, el COP alcanza un valor máximo, debido a la relación entre el efecto refrigeante y el traajo de compresión. Con los resultados de presión del refrigerante, se llegó a estimar un COP máximo de 8.58, cuando la presión y temperatura de entrada fueron 290.93 kPa y 18.7 °C, respectivamente, alcanzando un error inferior al 1 % con respecto al valor experimental.