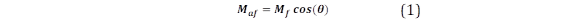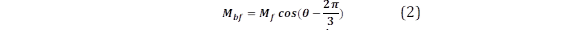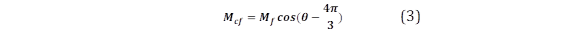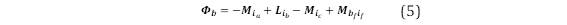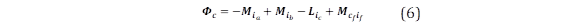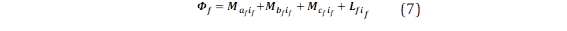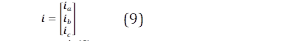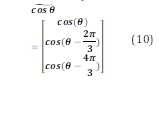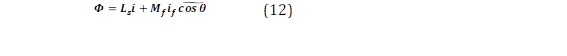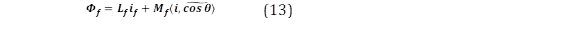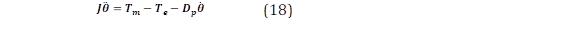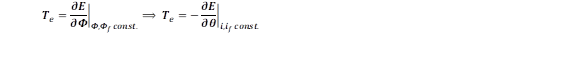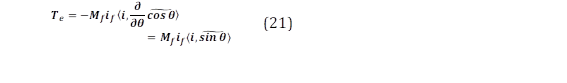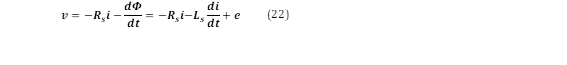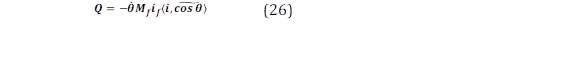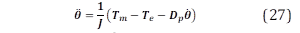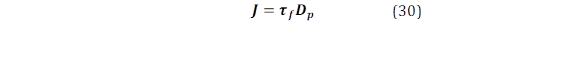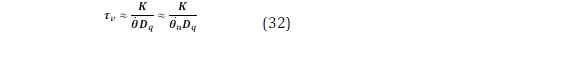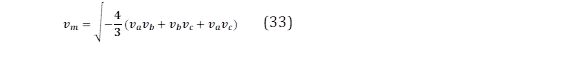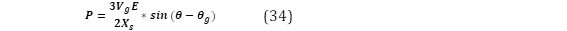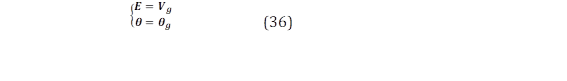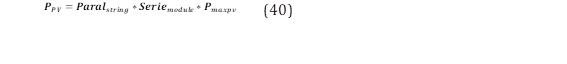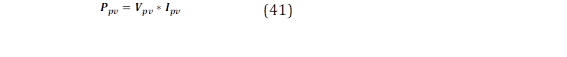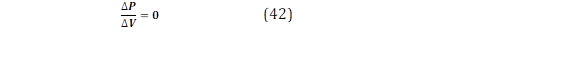INTRODUCCIÓN

El incremento sostenido en la demanda de energía a nivel mundial ha llevado a buscar y utilizar nuevas fuentes para satisfacer esta necesidad. Además, una alta dependencia de combustibles fósiles genera fuertes impactos en las economías de los países, y agrava su emisión de gases nocivos al medio ambiente. Como resultado, las fuentes de energías renovables (FER) han ido ganando más importancia y participación dentro de la generación de electricidad en la mayoría de países [1]- [2]. En este sentido, muchas investigaciones han sido enfocadas en mejorar la eficiencia de estas tecnologías, pero sobretodo en definir escenarios apropiados para su integración con las redes eléctricas convencionales [3].

Inicialmente, y como parte de la integración con la red, la generación a partir de FERs fue limitada a alimentar cargas puntuales o en ubicaciones remotas. Además, la variabilidad de los recursos naturales hace que la continuidad del servicio no pueda ser asegurada con las FERs [4]. Por otro lado, la generación en estos sistemas se hace directamente en corriente continua (CC), y no en corriente alterna (CA) como en la mayoría de centrales eléctricas convencionales, lo que dificulta su conexión directa a la red. De esta forma, las centrales de generación con FERs necesitan electrónica de potencia para convertir su energía e integrarse a las redes convencionales. Estos equipos se llaman conversores y presentan características muy versátiles para la operación de los sistemas de potencia modernos. Principalmente por su flexibilidad de control, costo accesible y la compatibilidad con las nuevas topologías de sistemas eléctricos como: generación distribuida (GD), micro-redes, o los sistemas eléctricos inteligentes [5].

Es precisamente la adopción de estas nuevas topologías lo que ha llevado a que los convertidores y la electrónica de potencia tengan una mayor participación en los sistemas actuales de transmisión y distribución [6]. Sin embargo, estos elementos no solo han incrementado los problemas en la calidad de energía, sino también han disminuido la inercia de los sistemas eléctricos de potencia (SEP). Limitando su respuesta ante variaciones de frecuencia y volviéndolos propensos a problemas de inestabilidad. De esta forma, los SEPs se han convertido en sistemas no lineales menos predecibles durante su operación dinámica [7]. En los antiguos SEPs, las partes giratorias de los generadores sincrónicos (GSs) eran vitales contra las variaciones de voltaje y frecuencia. Estas partes aportaban su inercia inherente y capacidad de amortiguación para garantizar la estabilidad de todo el sistema [8].

Para compensar esta falta de inercia, algunas investigaciones se han enfocado en desarrollar nuevos esquemas de control para conversores, o adaptar técnicas bien estudiadas en su operación. Normalmente, los controladores en plantas con FERs están diseñados para maximizar su generación e inyectarla totalmente a la red [9]-[10], pero esto es solo factible en redes con baja participación de FERs y donde las variaciones de potencia pueden ser compensadas por los controladores asociados a los generadores convencionales. De hecho, una participación mayoritaria de estos asegura el balance general y estabilidad del SEP [11].

En este contexto, dos técnicas han sobresalido para mitigar la falta de inercia en los SEP modernos durante los últimos años: Maquinas sincrónicas virtuales (VISMAs), y conversor sincrónico (CS) [12]. Ambas técnicas buscan imitar todas las características de los GSs, y añadir inercia virtual a los generadores de FERs [13]. Sin embargo, el CS resulta como una técnica de control más conveniente y simple porque genera un voltaje de referencia y provee amortiguación para mejorar la estabilidad de la red utilizando la electrónica de potencia del conversor CC/CA [14]. Es decir, el CS es capaz de comportarse como una fuente de voltaje controlada. Asimismo, su principal ventaja es que permite escoger los valores virtuales de parámetros como inercia, coeficiente de fricción, inductancia de campo e inductancia mutua en un rango más amplio, e inclusive pueden ser modificados durante la operación del sistema [15]. De esta forma, el CS se presenta como una técnica favorable para una transición sin problemas hacia una nueva red con una participación cada vez mayor de los conversores CC/CA [16].

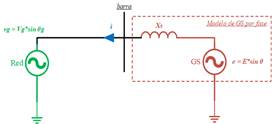
Otro requerimiento importante para la operación de los conversores es mantenerse sincronizados con la red, esta sincronización debe asegurarse antes y después de su conexión [17]. Entonces, el conversor será capaz de unirse a la red y suministrarle la cantidad exacta de energía, inclusive durante variaciones de frecuencia y voltaje [18]. Para este propósito, algunos autores como [19]-[20] proponen usar unidades específicas dentro de los controladores mediante un lazo de seguimiento de fase o PLL por sus siglas en inglés. No obstante, el uso de PLL aumenta la complejidad de los controladores y puede poner en peligro la estabilidad del sistema debido a una lenta sincronización [20]. Adicionalmente, los PLL pueden producir efectos no deseados en la operación de la red debidos a su naturaleza no lineal [21]. Por esta razón, una unidad de sincronización dedicada, rápida y efectiva sigue siendo todavía una tarea pendiente para la industria del control de los SEP. La Fig. 1a muestra la estructura y señales utilizadas para un controlador con unidad dedicada de sincronización.

Respecto a esta limitación, la técnica del CS toma mayor importancia porque al estar basada en el modelo matemático de una máquina sincrónica, este puede operar en modo generador y suministrar voltaje [21]. Por lo tanto, el controlador del CS puede ser considerado como un controlador con capacidad integrada de regulación de voltaje y frecuencia como la mayoría de controladores utilizados en las centrales térmicas o hidroeléctricas. Esto junto con el hecho que un GS puede ser sincronizado con la red, hace posible que se pueda eliminar la unidad específica de sincronización en el controlador del CS, convirtiéndole en un dispositivo con auto-sincronización. Consecuentemente, una estructura de control más compacta y libre de componentes no lineales es posible para conversores conectados a la red. La Fig. 1b muestra la estructura de control y señales utilizadas para este controlador.

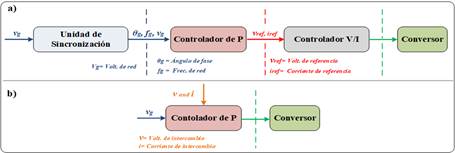
Figura 1: Estructuras de control y señales usadas en conversores conectados a la red. a) Conversores controlados como fuentes de voltaje o corriente con unidad dedicada de sincronización. b) Estructura de control compacta donde las funciones de sincronización, regulación de voltaje y frecuencia están integradas dentro del bloque de control de P 

Dentro del estado del arte, algunos estudios han abordado la auto-sincronización de los CSs. Por ejemplo, una de las primeras contribuciones aparece en [21], donde el modelo básico del CS es modificado para ser capaz de monitorear la frecuencia de la red antes y después de la conexión. Los resultados experimentales muestran que la efectividad en el monitorio de frecuencia se incrementa en un 65% con esta técnica. Un próximo estudio [22] propone una técnica de auto-sincronización basada en el ángulo de fase y aplicada a cargas locales. Específicamente, un controlador proporcional integral (PI) calcula los valores de compensación para las referencias de voltaje y frecuencia que son usados por una unidad de control durante la sincronización.

Otras investigaciones han aplicado también la técnica de CS en sistemas monofásicos. Es así que [23] conserva el modelo presentado en [21], pero incluye un limitador de corriente que previene problemas de sobrecorriente durante la conexión. Con esta limitación se soluciona una de las principales desventajas del modelo presentado en [21]. Otra aplicación monofásica es explicada en [24], misma que incluye un límite de saturación para la potencia entregada por el conversor considerando las características de control de caída del controlador.

Las investigaciones más recientes han buscado mejorar las ideas detalladas anteriormente, dando nuevos enfoques a la auto-sincronización. En particular, [25] mejora la respuesta dinámica del CS y limita la inyección de potencia activa (P) y reactiva (Q) en la red. Igualmente, el modelo limita la corriente inyectada durante la aparición de fallas mediante un lazo de corriente interno basado en resonancia proporcional. También se incluye un voltaje de retroalimentación dentro del lazo de corriente para asegurar una transferencia segura entre el funcionamiento autónomo o con conexión a la red.

Por otro lado, [26] propone un enfoque distinto para la auto-sincronización del CS donde solo se considera el voltaje interno del lado de la red, es decir no es necesario medir los ángulos de fase antes de unirse a la red. Para este fin, un grupo de resistencias virtuales es incorporado, el cual proporciona una retroalimentación virtual de P y Q al controlador durante la sincronización. La utilización de resistencias virtuales en lugar de inductancias virtuales permite una rápida auto-sincronización, y disminuye el número de parámetros que necesitan ser sintonizados para una correcta operación.

De la información establecida en los documentos consultados, se observa que la técnica de CS ha sido poco aplicada en SEPs con frecuencia nominal de 60 Hz. Asimismo, todos los modelos consultados utilizan fuentes ideales de voltaje en CC (baterías) para alimentar al circuito de potencia del CS. Sin embargo, y considerando la variabilidad de las FERs, esta aproximación no podría ser la adecuada para estudiar la respuesta de los CSs con auto-sincronización debido a que eventos transitorios podrían aparecer durante este proceso.

Como respuesta a esto, esta investigación busca reemplazar la batería en CC por un pequeño sistema fotovoltaico (FV) equipado con un controlador del punto de máxima potencia (MPPT) para alimentar el circuito de potencia del CS construido en MATLAB. De igual forma, el CS incluirá un controlador PI y una impedancia virtual para hacer posible la auto-sincronización con la red eléctrica, representada por un bus infinito en este modelo. Así, la respuesta dinámica de un CS auto-sincronizado conectado a una red eléctrica y planta de generación FER será probada. Especialmente, durante el momento de vinculación o durante variaciones de P y Q.

Finalmente, el resto del documento está organizado de la siguiente manera. La sección 2 detalla el modelamiento de una maquina sincrónica, la sección 3 explica de forma general del modelo matemático del CS, y la sección 4 describe el diseño y operación de un CS con auto-sincronización. En la sección 5 la modelación de la planta FV y el controlador MPPT en MATLAB es presentada. Mientras que las secciones 6 y 7 incluyen los resultados obtenidos junto con las conclusiones y trabajos futuros, respectivamente.

MODELAMIENTO MÁQUINA SINCRÓNICA

El modelamiento de las maquinas sincrónicas, especialmente de los GSs, es un tema bien estudiado dentro de la ingeniería eléctrica. Por ejemplo, [14] establece que los GSs pueden clasificarse en modelos que van desde el segundo hasta el séptimo orden dependiendo de su complejidad. El detalle del modelo a utilizarse depende del propósito del estudio y sus asunciones. De este modo, muchos autores consideran voltajes o corrientes balanceadas en estado estable para sus análisis. Usualmente, el enfoque clásico para modelar un GS utiliza el modelo de tercer orden porque garantiza una precisión adecuada, complejidad razonable y simplicidad para la formulación de ecuaciones matemáticas [27].

Bajo este contexto, y desde la perspectiva de análisis del sistema y diseño del controlador, esta investigación utiliza un sistema pasivo no lineal como modelo del GS, similar al mostrado en [11] y que mantiene las características de un modelo de tercer orden. El modelo incluye una máquina de rotor cilíndrico para mantener constantes las inductancias en el estator, y un par de polos por fase sin bobinado de amortiguamiento. Por lo tanto, no habrá efectos de saturación magnética en el entrehierro, o la aparición de corrientes de Eddy. Para mayor detalle, la modelación clásica de las partes eléctrica y mecánica del GS serán explicadas individualmente a continuación:

Parte Eléctrica

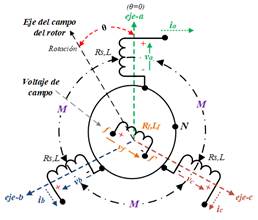
El campo magnético y los tres bobinados idénticos del estator se ubican en ranuras alrededor de la periferia de un espacio de aire, de acuerdo a la geometría presentada en [28]. Los bobinados del estator pueden representarse como bobinas con autoinductancia (L) e inductancia mutua (M). Normalmente, M es un valor positivo (M>0) igual a 1 2 L que recibe un signo negativo (-M) debido al retraso de fase (120֯ o 𝟐𝝅 𝟑 ). Por otra parte, el devanado del rotor se representa como una con autoinductancia de valor (L_f). Todos los elementos se muestran en la Fig.2.

Figura 2: Estructura de un GS trifásico ideal de rotor redondo  

Además, las inductancias mutuas entre la bobina del rotor y cada una de las bobinas del estator varían junto con el ángulo del rotor (θ) que usualmente toman valores iguales 𝟐𝝅 𝟑 y 𝟒𝝅 𝟑 ). Aclarando:

En estas expresiones M_f toma valores positivos, es decir mayores a cero (M_f > 0). De igual forma, el enlace de flujo viene dada por:

Donde i_a, i_b y i_c son las corrientes de fase del estator e i_f es la corriente de excitación del rotor. Algunas expresiones (corrientes, enlaces de flujo, senos y cosenos) pueden escribirse de forma matricial para simplificar futuras expresiones, como se muestra a continuación:

Es importante mencionar que este modelo no incluye línea de neutro, entonces la suma de las corrientes de fase del estator es igual a cero (i_a + i_b + i_c=0). Con estas consideraciones algunas expresiones pueden reescribirse, por ejemplo, el enlace de flujo del estator.

Considerando que L_s=L+M, el enlace de flujo del campo (Φ_f) puede escribirse como se muestra en (13).

Donde el símbolo :,: representa el producto interno dentro de los límites de ℝ³ lo que quiere decir:

La reacción de la armadura está representada por 𝑴 𝒇 𝒊, 𝒄𝒐𝒔 𝜽 , y es constante si las corrientes de fase están balanceadas y son funciones sinusoidales del ángulo θ. Por otro lado, y asumiendo que R_s es la resistencia de los devanados del estator, la matriz de los voltajes terminales 𝒗= 𝒗 𝒂 𝒗 𝒃 𝒗 𝒄 𝑻 puede obtenerse a partir de (12) c

Donde la fuerza electromotriz (FEM) es 𝒆= 𝒆 𝒂 𝒆 𝒃 𝒆 𝒄 𝑻 y es generado por el movimiento del rotor dado por la expresión (16).

Cabe mencionar que el vector voltaje e también es conocido como el voltaje interno sincrónico o de carga cero. Por último, el voltaje terminal de campo puede obtenerse a partir de (13) y expresarse en (17).

Donde R_f es la resistencia del devanado del rotor. Sin embargo, 𝒗 𝒇 no será utilizado en el modelo digital porque 𝒊 𝒇 lo reemplazará como un valor de entrada ajustable. Todas estas ecuaciones completan el modelo eléctrico del GS modelado.

Parte Mecánica

El comportamiento mecánico del GS está regido por la ecuación de oscilación mostrada en (18).

Donde el momento de inercia de todas las partes rotativas relacionadas con el rotor es 𝑱. T_m representa el torque mecánico, T_e es el torque electromagnético, y D_p es el factor de atenuación. Adicionalmente, T_e puede estimarse de la energía (E) almacenada en el campo magnético de los GSs.

Siguiendo esta expresión y algunas consideraciones energéticas mostradas en [29]. Es simple deducir que:

En este contexto, T_e viene dada por (21).

MODELAMIENTO MATEMÁTICO DE CONVERSORES SINCRÓNICOS (CSs)

Para que un conversor funcione como CS, este debe ser capaz de usar su dinámica. De igual manera, esta tecnología hace que un generador operado con un conversor basado en electrónica de potencia se vea como un GS convencional desde el lado de la red, conservando las ventajas y desventajas de los GSs [8]. El modelo matemático del CS presentado en este trabajo utiliza un conversor simple CC/CA para transformar la potencia generada en CC en una potencia trifásica en CA.

Este conversor incluye tres ramas de inversión controladas con modulación por ancho de pulso (PWM) y filtros LC para reducir los picos de corriente y voltaje durante la operación de los interruptores según [8] y [11]. Además, la impedancia y resistencia de la red están representadas por L_g y R_g, respectivamente. Elementos que se consideran luego de que el interruptor (CB) se cierra y conecta con un generador ideal (sistema barra infinita). El diagrama del conversor se muestra en la Fig.3.

En la Fig. 3, el rectángulo con línea punteada azul muestra la parte de potencia del CS, misma que está alimentada por una planta FV que es optimizada por un controlador MPPT.

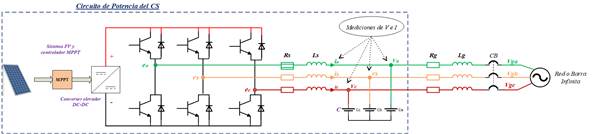
Figura 3: Circuito de potencia del CS en un conversor trifásico, incluyendo los filtros LC, sistema FV y controlador MPPT 

Este circuito tiende a funcionar como un GS conectado en paralelo con capacitores si el efecto transitorio no es considerado. Adicionalmente, el sistema FV y el controlador MPPT son incluidos para representar la potencia extraída del rotor primario imaginario y la inercia absorbida desde las partes giratorias del GS virtual. Por otra parte, debe recalcarse que L_g y R_g no son elementos del CS, pero tienen un rol importante durante la sincronización y el control de potencia desde el lado de la red eléctrica. La modelación matemática del CS puede dividirse en dos etapas principales: parte de potencia y electrónica, respectivamente.

Parte de Potencia

En este caso, los voltajes terminales (𝒗= 𝒗 𝒂 𝒗 𝒃 𝒗 𝒄 𝑻 ) del GS virtual se obtienen a partir de los capacitores conectados en paralelo de la Fig.3. Es así que (22) puede usarse para el cálculo de estos voltajes.

La impedancia del bobinado del estator es representada por L_s y R_s. Luego, e_a, e_b, y e_c buscan emular la FEM producida por el movimiento del rotor imaginario. Esto es posible porque los tiempos de operación de los diodos de potencia se diseñan para tener un valor de e de acuerdo a (23) y sin tener mucha dependencia de la técnica de PWM.

Como se estableció anteriormente, la corriente de campo (i_f) es usada en lugar del voltaje de campo (v_f) para alimentar el bobinado del rotor imaginario del CS en esta investigación. Entonces, y si i_f permanece constante, (23) puede ser reducida en (24), donde 𝜽 es la velocidad angular virtual del modelo y M_f representa la inductancia mutua.

Parte Electrónica

En esta parte del modelo, se utilizan se utilizan los valores presentados en la sección anterior para calcular P y Q siguiendo (25) y (26).

También, la ecuación de oscilación es reescrita para obtener (27) en donde T_m es el torque mecánico, T_e el torque eléctrico y D_p un factor de amortiguamiento. J Describe el momento de inercia de las partes rotativas en relación con el rotor haciendo que T_m se convierta en una señal de control de entrada, mientras que T_e es dependiente de i y θ según (28). En ambas expresiones el enlace de flujo, corrientes, así como las funciones seno y coseno están escritas de forma matricial.

El modelo más básico de un CS debe incluir las expresiones (24), (26) y (28) en su parte electrónica. En este sentido, puede decirse que la corriente en los inductores (i), voltaje en capacitores (v), el ángulo virtual (θ) y 𝜽 son las variables de estado del CS. Por el contrario, T_m y M_fi_f son las entradas de control del modelo. Un funcionamiento adecuado del CS es obtenido cuando el controlador genera las señales para T_m y M_fi_f de tal forma que la estabilidad del sistema es mantenida, inclusive siguiendo las variaciones de P y Q [11]-[14].

El mecanismo utilizado en los CSs para compartir la carga proporcionalmente respecto a su potencia nominal es variar la P entregada a la red de acuerdo a su frecuencia. Este enfoque de control se denomina “caída de frecuencia”. Similarmente, reducir el valor de Q de forma lineal con el incremento del voltaje es otra técnica llamada “caída de voltaje”. Las secciones 3.3 y 3.4 explican la implementación de estas técnicas en el modelo matemático del CS.

Regulación de P con la Técnica de Caída de Frecuencia

Es conocido que la velocidad del rotor es preservada por la fuerza motriz en los GSs, y que D_p es causado por la fricción mecánica. De esta forma, y bajo la perspectiva del control de caída de frecuencia, cuando la demanda de P crece, la velocidad de los GSs cae debido al incremento de T_e según (28). Como resultado, la regulación de la potencia del sistema incrementa la potencia mecánica hasta alcanzar un nuevo balance. Los valores típicos de caída de frecuencia tienen un aumento del 100% de potencia por una disminución de frecuencia de entre el 3% y 5% en términos de valores nominales [11].

En el modelo básico de un CS, el control de caída de frecuencia compara la velocidad angular virtual ( 𝜽 ) con la frecuencia angular de referencia ( 𝜽 𝝉 ) que generalmente es igual a la frecuencia nominal de la red ( 𝜽 𝒏 ). Esta diferencia es multiplicada por D_p y añadida a T_m. D_p es usada para ajustar el flujo de P desde el inversor de acuerdo con la desviación de la frecuencia de la red respecto a un valor de referencia. De igual forma, D_p representa físicamente a la suma de los coeficientes de fricción mecánica y de caída de frecuencia. Por lo tanto, si se denota la variación en el torque total del rotor imaginario con ΔT y el cambio en la frecuencia angular con ∆𝜽 , D_p se puede expresar como:

Mientras que T_m se obtiene a partir del valor de referencia de P, denominado P_set, dividido para velocidad mecánica nominal 𝜽 𝒏 . Sin embargo, en el modelo propuesto, 𝜽 es usada debido a que la diferencia entre sus valores es despreciable. En el caso de los CSs, el lazo de regulación para P se vuelve simple debido a la no presencia de partes mecánicas, y a que i es la única variable a ser medida.

Complementariamente, el mecanismo de regulación para P tiene una estructura anidada. El lazo interno de la estructura se encarga de la caída de frecuencia usando D_p como retroalimentación. Mientras que, el lazo exterior es un poco más complejo y tiene como retroalimentación a i a partir de T_e. La constante de tiempo para el lazo de caída de frecuencia es 𝝉 𝒇 = 𝑱 𝑫 𝒑 , a partir de esto se puede establecer que:

La ventaja es que 𝝉 𝒇 puede tomar valores más pequeños que los GSs reales porque no hay un retardo intrínseco asociado al lazo de caída de frecuencia. En el caso de los CSs no son necesario grandes valores de inercia como en los GSs convencionales, donde un valor grande de inercia indica mayor presencia de energía mecánica almacenada. Normalmente, la inercia en CSs es implementada con sistemas de almacenamiento de energía, baterías, pero esta investigación usará el sistema FV para este fin, dándole un grado de novedad a este trabajo.

Regulación de Q con la Técnica de Caída de Voltaje

Un concepto muy parecido al anterior es aplicado en esta sección. La Q entregada por el CS es controlada usando un coeficiente de caída de voltaje (D_q) que representa la relación entre la variación de la Q requerida (𝜟𝑸) y el cambio del voltaje (𝜟𝑽) de la siguiente forma:

Para el lazo de control de Q, el error de la amplitud de voltaje debe ser medido (v_m), y luego utilizado para calcular la diferencia entre el voltaje de referencia (v_r) y el voltaje de retroalimentación (v_fb), usualmente igual al voltaje de red (v_g). El valor obtenido es multiplicado por D_q y sumado al valor de referencia de Q (Q_set) junto con el valor de Q obtenido en (26). El resultado es usado como señal de entrada para la integral con ganancia 𝟏 𝑲 donde se obtiene M_f i_f. En esta investigación Q no es medida, sino calculada a partir de i y θ en Simulink.

El control de Q también presenta una estructura anidada, donde v_fb ≈ e y v_m ≈ 𝜽 M_f i_f si se ignora el efecto de los filtros LC. Siendo el lazo interno el lazo de amplitud de voltaje, y el lazo externo el lazo de Q. En esta estructura, la constante de tiempo del lazo de voltaje ( 𝝉 𝒗 ) viene dada por la siguiente expresión:

El error de la amplitud de voltaje está dado por (33) considerando que los voltajes terminales están debidamente balanceados.

DISEÑO Y OPERACIÓN DEL CONVERSOR SINCRÓNICO AUTO-SINCRONIZADO SIN PLL

Considerando que un CS imita la operación de un GS, la conexión de un GS a un sistema de barra infinita puede ser utilizada para explicar la sincronización de un CS con la red eléctrica (Fig.4). En esta topología, P y Q pueden ser calculadas a partir de:

Figura 4: Modelo por fase de un GS conectado a una barra infinita [21]  

Donde V_g es el voltaje de la barra infinita, E el voltaje inducido en el GS, X_s la reactancia sincrónica del GS y los ángulos de fase para la red y el GS son θ_g y θ, respectivamente. De estos valores se puede definir la diferencia de fase como: 𝜹=𝜽− 𝜽 𝒈 . Finalmente, V_g y θ_g son usados como referencia para E y θ en el cálculo de P y Q con (25) y (26).

Sabiendo que T_m y 𝜹 tienen un relación directa con la potencia entregada por la red, puede decirse que si uno de estos parámetros se incrementa, los otros también lo harán. De igual forma, se sabe que la potencia real entregada por la red podrá incrementarse solamente hasta igualar la potencia mecánica de la turbina y que el máximo valor de 𝜹 será 𝝅 𝟐 𝒓𝒂𝒅 sin pérdida de sincronismo. Por otro lado, la regulación de Q se hace limitando el intercambio de Q entre la red y el GS. Todo esto de cumple cuando:

Las condiciones presentadas en (36) suceden cuando P y Q son cero, además cuando el voltaje generado (e) es igual a v_g, condiciones que no son comunes durante la operación normal. Sin embargo, y de alcanzarse, el GS puede ser fácilmente conectado o desconectado de la red sin producirse grandes efectos transitorios. Si esta condición es aplicable a un GS, entonces también puede aplicarse para la sincronización de un CS sin el uso de PLL. A continuación, el controlador para un CS con auto-sincronización es explicado basado en este enfoque y la teoría de la sección 3.

Controlador de un Conversor Sincrónico con Auto-Sincronización sin PLL

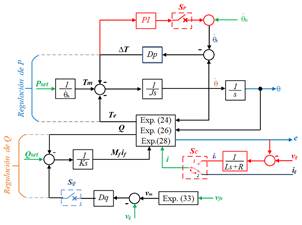
La Fig. 5 muestra el controlador propuesto, mismo que incluye nuevas etapas para una conexión segura con la red y eliminar la necesidad de una unidad dedicada de sincronización o PLL. En este contexto, se ha añadido una corriente virtual (i_s) generada a partir de e y v_g, así el controlador puede alimentarse con i_s o la corriente de la red (i_g) - bloque inferior resaltado en color rojo. Asimismo, un controlador PI se añade a la salida de ∆T en el bloque de caída de frecuencia que ayudará a que D_p sea cero durante la sincronización y enviar una correcta frecuencia de referencia para el modelo básico del CS (estructura con línea negra) - bloque superior resaltado en color rojo.

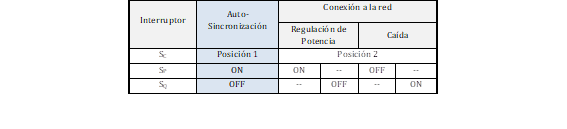
Igualmente, el controlador tiene tres interruptores S_C, S_P, y S_Q que permiten escoger el modo de operación del controlador. Por ejemplo, si S_C está en la posición 1, S_P encendido y S_Q apagado, el controlador estará operando de acuerdo a la teoría explicada en la sección 3. Además, si P_set y Q_set son cero, la sincronización con la red es posible y este modo se conocerá como el modo de auto-sincronización. La versatilidad del controlador radica en la posición 2 de S_C porque el CS puede tener cuatro modos de operación en este escenario. La Tabla 1 resume los modos de operación en función de la posición de los interruptores.

Figura 5: Diagrama de bloque de controlador del CS con auto-sincronización  

Tabla 1: Modos de operación del CS auto-sincronizado [30] 

Sincronización antes de la Conexión con la Red Eléctrica sin PLL

En la práctica, la sincronización de un GS es posible si este tiene el mismo voltaje, frecuencia y secuencia de fases con la red a conectarse. Generalmente, equipos de medición y sincronoscopios son utilizados para verificar estas condiciones. Aplicando el mismo concepto a los CSs, se tiene que e debe ser igual a v_g. Específicamente, el valor de E sea el mismo que V_g, a fin de que e y v_g mantengan la misma secuencia de fase. Asimismo, los valores de referencia P_set y Q_set deberán ser cero. Con estas consideraciones se elimina la necesidad de usar PLL para la sincronización del CS.

No obstante, el valor de i_g debe también ser cero hasta que el interruptor de acople se cierre por lo que ninguna regulación puede hacerse durante este tiempo. Para superar esta limitación, una impedancia virtual por fase se añade al modelo y hacer posible la conexión del CS con la red. Esta impedancia virtual tiene un inductor de la forma L_s+R, y su corriente (i_s) puede calcularse con (37).

i_s reemplazará a ig como corriente de retroalimentación en (26) y (28) para el cálculo de Q y T_e. Al mismo tiempo, S_P deberá mantenerse encendido para que P_set=0, y S_Q apagado para que Q_set=0 (columna dos-Tabla 1). De esta forma, e se sincronizará con v_g.

En términos simples, cuando i_s es cero o tiene un valor cercano a 0, el CS está en sincronismo con la red eléctrica. Después que esto sucede, el interruptor de acoplamiento puede ser cerrado (CB) y el CS está unido a la red. Luego, el interruptor S_C debe pasar a la posición 2 para permitir que i_g alimente el controlador durante la operación normal del sistema. A partir de aquí, los interruptores pueden operarse a conveniencia para fijar cualquiera de los modos de operación detallados en la Tabla 1.

Operación luego de la Conexión con la Red Eléctrica

Luego de unirse a la red, el controlador usa T_m y P_set para regular el valor de δ, siguiendo la siguiente expresión.

Donde 𝜽 𝒏 es la frecuencia nominal de la red. En el caso de que el interruptor S_P = ON, el controlador PI asegurará que ∆T sea cero en estado estable. Considerando

Aquí, representa la salida del controlador PI. Si el controlador trabaja correctamente, P=P_set porque δ tiene un valor constante. Caso contrario, si S_P = OFF, el controlador PI es omitido y el CS trabaja en el modo de caída de frecuencia descrito en 3.3. En ambos casos, (38) puede usarse para definir la frecuencia del CS porque S_Q está apagado y δ es menor que 𝝅 𝟐 𝒓𝒂𝒅. Esto se indica en la tercera y cuarta columna de la Tabla 1.

Otra consideración importante, a partir de (34), es que el P entregado por el CS es proporcional al seno δ, al igual que T_e. De esta forma, y para 𝜹 𝝐 − 𝝅 𝟐 , 𝝅 𝟐 , T_e aumenta para valores positivos de δ, y disminuye para valores negativos. Para la misma expresión, δ y T_e aumentaran si 𝜽 𝒈 disminuye. Por esta razón, la señal de entrada al bloque integral 𝟏 𝑱 𝒔 tiene un valor pequeño y la frecuencia del CS ( 𝜽) disminuye. Esto se repite hasta que las frecuencias de red y del CS sean iguales (𝜽 = 𝜽 𝒈 ) , y 𝜽 converja siempre hacia 𝜽 𝒈 para el intervalo 𝜹 𝝐 − 𝝅 𝟐 , 𝝅 𝟐 . De esta forma no se necesita una unidad de sincronización que entregue 𝜽 𝒈 como frecuencia de referencia al CS.

En el caso de Q, el controlador del CS con auto-sincronización mantiene la lógica presentada en 3.4 de acuerdo a la posición del interruptor S_Q. Si S_Q = OFF, los parámetros a ser controlados son los mismo presentados en 3.4 y la Q generada puede seguir al valor fijado como Q_set. Por otro lado, la función de caída de voltaje está activada si S_Q = ON y una desviación de voltaje (∆𝑽= 𝑽 𝒏 − 𝑽 𝒈 ) es considerada para calcular M_fi_f. En este escenario Q no será igual a Q_set y corresponden a la quinta y sexta columna de la Tabla 1.

Modelación del Conversor Sincrónico con Auto-Sincronización en Simulink-MATLAB

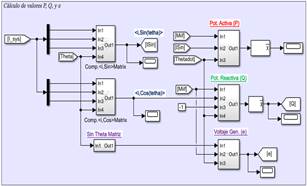
La teoría explicada en la sección 3 y los apartados anteriores es aplicada para construir el modelo matemático del controlador en Simulink-MATLAB. Dentro de Simulink cuatro diferentes bloques fueron construidos para replicar la estructura de control de la Fig.5.

El primer bloque será el encargado de la regulación de P, el segundo bloque regulará la Q, el tercer bloque calcula todos los parámetros eléctricos detallados en la teoría. Para terminar, el cuarto bloque corresponde a la impedancia virtual donde los elementos de L_s+R son modelados con la ayuda de una función de transferencia vinculada a un archivo de extensión .M en el ambiente de trabajo de MATLAB. Debido a la limitación de páginas no es posible mostrar todos los bloques modelados, pero la Fig.6 muestra parte del modelo desarrollado (bloque 3). Además, los parámetros de la red y del conversor para el modelo son resumidos en la Tabla 2.

Figura 6: Bloque para el cálculo de P, Q y e del CS con Auto-Sincronización - Simulink 

Tabla 2: Valores de los Parámetros Internos del CS con Auto-Sincronización [11]-[21]  

DISEÑO Y OPERACIÓN DEL SISTEMA FV CON EL CONTROLADOR MPPT

En este apartado, la modelación de un sistema FV con una potencia nominal de 125 kW conectado al CS auto-sincronizado por medio de un convertidor elevador es explicada. Adicionalmente, un controlador MPPT básico es incorporado al convertidor elevador usando la “MATLAB Function” para programar su algoritmo en el entorno de Simulink. Ambos sistemas alimentan al CS y son la fuente de energía de donde la inercia virtual es extraída. Para este trabajo, no se han considerado variaciones en los niveles de radiación solar y el control del rizado del voltaje en CC. Debido al incremento en la complejidad del controlador, estos aspectos serán abordados en trabajos futuros.

Sistema Fotovoltaico

La potencia máxima del arreglo FV es exactamente 125,93 kW y emplea tres paneles solares de Atlantis Energy Systems del tipo TS125LM. Específicamente, el sistema está compuesto por un arreglo en paralelo con tres paneles conectados en serie. La expresión (40) muestra el cálculo de la potencia máxima del sistema (P_PV) considerando el número de paneles conectados en paralelo y serie junto con la potencia máxima de cada panel (P_maxpv) [4].

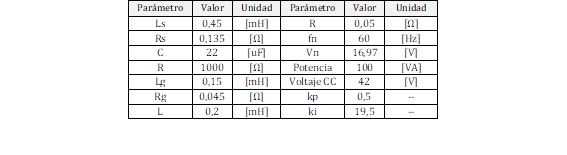
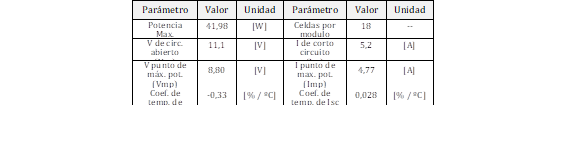
Es importante resaltar que otra consideración principal para el diseño del sistema FV es no exceder el voltaje CC del CS. Bajo este escenario, el bloque “PV array” de Simulink es usado para modelar el sistema FV diseñado. Este bloque requiere información de la radiación solar y temperatura ambiente que han sido asignados de acuerdo a los valores usados en las condiciones estándar de prueba (STC), 1000 W/m² and 25° C, respectivamente. La Tabla 3 muestra los principales parámetros de los paneles fotovoltaicos utilizados.

Tabla 3: Información Técnica de los Paneles Fotovoltaicos de Energy Systems TS125LM - Simulink  

Controlador MPPT

El principal objetivo de este controlador es mantener la potencia generada por el sistema FV en su máximo punto a pesar de las variaciones durante la operación. Para este fin, y en términos simples, el controlador modelado usará el voltaje (V_pv) y corriente (I_pv) del sistema FV para calcular la potencia generada (P_pv).

Después, P_pv determina el ancho de pulso para la modulación PWM conectada directamente a los elementos de electrónica de potencia de un convertidor elevador CC-CC. Aquí, la consideración es que la relación entre la variación de la potencia generada y el voltaje de operación debe der igual a cero [31].

Para cumplir este propósito, el algoritmo de perturbación y observación (P&O) es aplicado al controlador por medio de una secuencia programada dentro de un “MATLAB function”. El algoritmo P&O es iterativo y calcula P_pv para cada instante de tiempo (t). Luego, lo compara con el valor de potencia obtenido para t-1. Si ∆P es diferente de cero, una variación sobre el voltaje de es aplicada hasta que devolver la diferencia a cero [31].

Convertidor Elevador CC-CC

Un convertidor elevador es un equipo electrónico que transforma una entrada de voltaje CC menor por una salida de voltaje CC de mayor amplitud. Esto se logra a través de la energía almacenada en un inductor como campo magnético que luego se transmite a una carga usando circuitos de conmutación de alta frecuencia. Este elemento es necesario dentro del CS modelado para alimentarlo con 42 V, y considerando que la salida de voltaje del sistema FV son solo 26,4 V.

La topología básica de este conversor aparece en la Fig.7. La primera rama del circuito tiene una resistencia y un capacitor (C) conectados en serie, mientras que un inductor (L) está conectado el paralelo a esta rama. El circuito de conmutación está compuesto por transistores de potencia, usualmente IGBT, que son controlados por un PWM retroalimentado por el controlador MPPT. En el lado de la carga, se ubica otro capacitor igual a C que está conectado en paralelo con una resistencia (R) [32].

Figura 7: Topología básica del convertidor elevador CC-CC  

Para el diseño del convertidor elevador usado en esta investigación, algunas consideraciones y valores son fijados previamente. De esta forma, la frecuencia de conmutación (f_sw) será 5 kHz, el voltaje de entrada (V_in) igual a 26,4 V, el voltaje de salida (V_out) será 42 V, y la eficiencia del convertidor (ⴄ) del 90% para considerar las corrientes parasitas del circuito.

Igualmente, la potencia máxima del convertidor elevador se asume igual a P_pv, y que la corriente de ondulación (I_ripple) será igual al 40% de la corriente de salida del convertidor (I_out). Con estos detalles se determina los valores de C, R, y L del circuito además del ancho de pulso para su circuito de conmutación. El detalle de los cálculos será incluido en futuras publicaciones debido al límite de páginas, pero la Tabla 4 resume los valores obtenidos para esta aplicación.

Tabla 4: Parámetros Calculados para el Convertidor Elevador CC-CC 

RESULTADOS DE LA SIMULACIÓN

Las teorías y conceptos mostrados anteriormente son probados usando simulaciones computacionales. Para esto, Simulink-MATLAB es utilizado para verificar la correcta operación del CS con auto-sincronización, la planta FV, conversor elevador CC-CC, y el controlador MPPT. Dentro del programa, modelos en tiempo discreto son utilizados, y el “solver” ode23tb con una tolerancia relativa de 10^-3 y un paso de tiempo de 1e^-5 son considerados para ejecutar el modelo.

Los valores para los coeficientes de tiempo y amortiguamiento se establecen de la siguiente forma. D_p es igual a 0,2026 que representa que una caída de frecuencia de 0,5% genera un incremento del 100% de P. Por otro lado, D_q es 117,88 y generará un aumento del 100% de Q con una caída de voltaje del 5%. También, 𝝉 𝒇 y 𝝉 𝒗 tendrán valores iguales y será 0,002.

La simulación empieza al instante t=0 con el interruptor S_C en la posición 1, S_P=ON, y S_Q=OFF para cumplir la condición de auto-sincronización (columna II - Tabla 1). Junto a esto los valores de P_set y Q_set son fijados en cero durante este tiempo. Se espera que luego de un tiempo, el CS pueda sincronizarse con la red de forma autónoma. Al tiempo t=2 el interruptor de acoplamiento se cierra y el interruptor S_C se cambia a la posición 2. Luego, la simulación continua con la inyección de P al tiempo t=5 por medio de un generador de señal que cambia el valor de P_set=80 W, y para terminar se inyecta Q al tiempo t=10 con un valor de Q_set=60 Var.

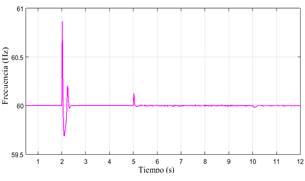
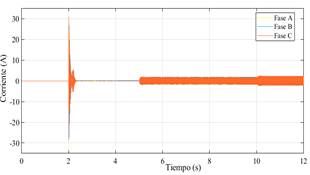
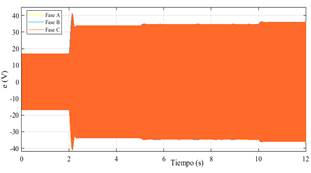
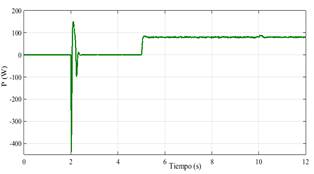
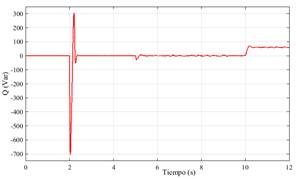
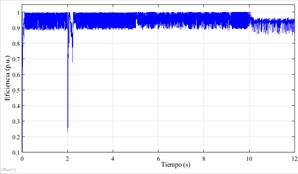
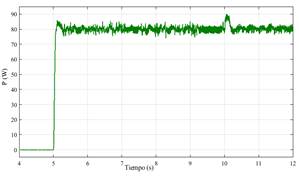
La respuesta del sistema se muestra desde la Fig. 8 hasta la Fig. 12, donde se observa que el CS es capaz de seguir la frecuencia de la red durante toda la secuencia de la simulación (Fig.8). De igual forma, se confirma que el CS opera en el modo de auto-sincronización durante los primeros instantes de la simulación, y la i_s es reemplazada por la i_g tan pronto como el CS se conecta con la red (Fig.9). Sin embargo, un evento transitorio sucede luego de cerrarse el interruptor al t=2, y la transición no es tan suave como se espera en la etapa de diseño. Dos principales razones podrían ocasionar esta respuesta, la primera relacionada a la eficiencia del algoritmo usado en el controlador MPPT para controlar la respuesta del sistema FV cuando se conectan cargas al sistema, como se muestra en la Fig.13. La segunda razón podría estar relacionada a una mala sintonización de los parámetros de la impedancia virtual (L_s+R). El comportamiento del voltaje e aparece en la Fig. 10 donde se ve que el voltaje aumenta súbitamente luego del cierre del interruptor, pero luego es capaz de retomar el valor nominal presentando luego ligeras variaciones durante la secuencia de simulación. Fig. 11 y Fig. 12 presentan los comportamientos de P y Q durante toda la simulación, confirmando la presencia del evento transitorio.

Figura 8: Frecuencia del sistema y CS con auto-sincronización 

Figura 9: Corriente del sistema y CS con auto-sincronización 

Figura 10: e generado en el controlador del CS con auto-sincronización 

Figura 11: P generada en el controlador del CS con auto-sincronización 

Figura 12: Q generado en el controlador del CS con auto-sincronización 

Figura 13: Eficiencia del controlador MPPT del sistema FV 

Para mayor detalle de la operación del CS, las Fig. 14 y Fig.15 muestran las respuestas de P y Q desde t=4 hasta el t=12. Aquí, se confirma que el CS es capaz de responder rápidamente ante las variaciones de las potencias inyectadas en t=5 y t=10 segundos, luego de unirse a la red eléctrica. Para P, el CS es capaz de mantener el valor de referencia (80 W) durante casi todo el tiempo de simulación, solamente variaciones de decenas de watts aparecen cuando la regulación de caída de frecuencia actúa. En el caso de Q, se observa una caída en su valor en alrededor de 30 Var, 50% del valor de referencia, durante la inyección de P. Reacción que está asociada al incremento del voltaje e (Fig.10) y la actuación del control de caída de voltaje. Además, al t=10, el CS sigue el valor de referencia de Q, pero no alcance el valor referenciada debido a las perdidas intrínsecas asociadas a los elementos usados en el circuito.

Figura 14: P generada en el controlador del CS con auto-sincronización desde t=4 hasta t=12 

Figura 15: Q generada en el controlador del CS con auto-sincronización desde t=4 hasta t=12 

CONCLUSIONES Y RECOMENDACIONES

En esta investigación, un nuevo enfoque para la sincronización de los CSs con las redes eléctricas de 60 Hz es presentada y científicamente sustentada. Este enfoque permite eliminar una unidad dedicada de sincronización o PLL. De esta forma, se asegura una operación más simple del controlador y sin grandes esfuerzos computacionales.

La capacidad de auto-sincronización permite a los CSs sincronizarse con la red eléctrica autónomamente monitoreando su frecuencia antes y después de la conexión. De igual forma, los CSs se vuelven en equipos más versátiles ya que pueden operar en diferentes modos con el cambio de posición de los interruptores S_C, S_Q y S_P. Adicionalmente, esta investigación es una de las primeras en incluir una planta de generación renovable como fuente de inercia virtual y aplicar el enfoque en sistemas con frecuencia nominal de 60 Hz. Aunque queda pendiente la simulación de variación del recurso solar y el rizado del voltaje CC en el controlador MPPT.

De todas formas, los resultados obtenidos sugieren que los parámetros de la impedancia virtual usada en este modelo deben ser cuidadosamente calculados cuando se usan sistemas renovables para alimentar a los CSs. Además, se requiere incorporar en el modelo una metodología para sintonizar convenientemente los parámetros de Ls+R. Esto ayudará a limitar los efectos transitorios durante el acoplamiento con la red e incrementará la robustez del modelo propuesto.

Finalmente, los trabajos futuros en este tema se enfocarán en aplicar el modelo sobre sistemas de potencia con valores nominales típicos en sistemas de distribución o transmisión para determinar su viabilidad de uso. En este mismo sentido, se buscará sustituir el esquema de barra infinita por un grupo de generadores modelados con sus respectivos sistemas de control para realizar estudios de estabilidad de frecuencia y voltaje más exhaustivos. Así como también, el uso de las curvas típicas de P y Q en el sistema fotovoltaico para un mejor análisis durante las variaciones de frecuencia o recurso solar.