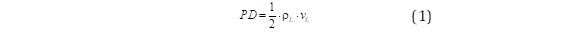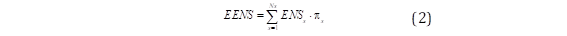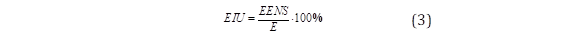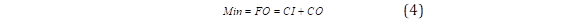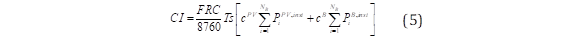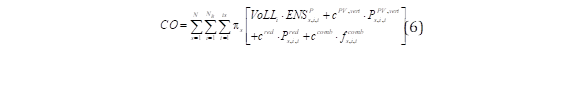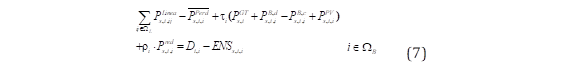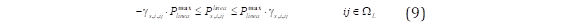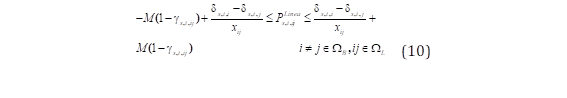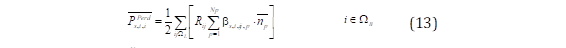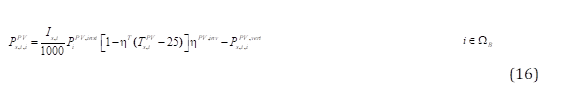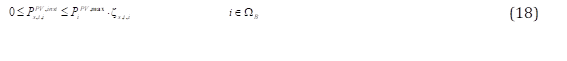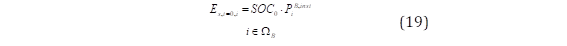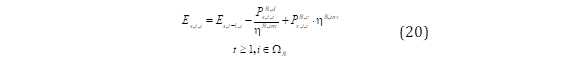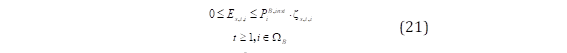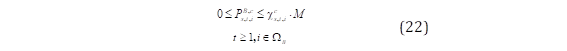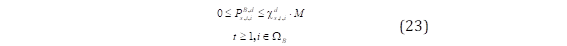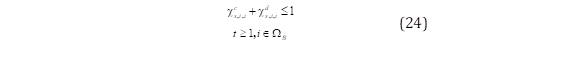INTRODUCCIÓN

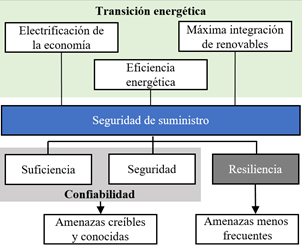
La energía eléctrica es un factor clave para el desarrollo de las sociedades modernas, ya que influye directamente sobre su crecimiento económico y la calidad de vida de sus habitantes. Estos ámbitos están estrechamente condicionados a una creciente dependencia energética, por lo cual se ha vuelto indispensable asegurar un suministro energético en concordancia con las metas planteadas a nivel mundial para una transición energética responsable y resiliente. En un contexto de transición energética, la mejora de la seguridad de suministro energético se ha vuelto un tema de mayor preocupación para gran parte de los gobiernos del mundo [1]. Por esta razón, el desarrollo de redes eléctricas resilientes que sean capaces de responder a situaciones climáticas cada vez más adversas (producto del cambio climático) es la apuesta para mejorar los niveles de seguridad y calidad de suministro eléctrico. La Fig. 1 muestra un nuevo marco conceptual de transición energética y resiliencia en redes eléctricas. Este marco se alinea con las exigencias de adaptar el sistema eléctrico a la nueva realidad climática (provocado por un aumento en los eventos climáticos extremos y desastres naturales) con estrategias que permitan transitar a la carbono neutralidad considerando la electrificación de la economía, la integración masiva de energías renovables y la eficiencia energética.

Los recursos energéticos distribuidos o DERs (del inglés Distributed Energy Resources) son fuentes de generación distribuida, así como dispositivos de almacenamiento que son capaces de desempeñar un rol clave para el incremento de la resiliencia frente a eventos exógenos de baja probabilidad y alto impacto (HILP, del inglés High Impact Low Probability) como los desastres naturales. Además, los DERs representan energía local, descentralizada, acentuando el rol de las comunidades y de las regiones en la descarbonización y la transición energética. De hecho, generar, almacenar y controlar energía localmente sin la necesidad de largas líneas de transmisión puede provocar que la red sea menos vulnerable a desastres y que la respuesta a una emergencia sea mucho más rápida y eficiente [2].

En ese sentido, existen varios trabajos que proponen diferentes métodos para mejorar la resiliencia de las redes eléctricas a través de la planificación y operación de DERs [3]. Por ejemplo, en [4] se presenta una propuesta para mejorar la resiliencia de las redes de distribución de energía eléctrica, aprovechando la naturaleza distribuida de los sistemas fotovoltaicos (PV, del inglés Photovoltaic) y el almacenamiento por baterías o BESS (del inglés Battery Energy Storage System). En este contexto, los recursos BESS ofrecen flexibilidad operativa adicional para mejorar la resiliencia durante la ocurrencia de eventos HILP debido a sus características de alta eficiencia, respuesta rápida y bajos costos de mantenimiento. No obstante, actualmente los costos de inversión de los sistemas de almacenamiento BESS son relativamente caros y escalan conforme al tipo de tecnología de baterías que se desee implementar (litio, plomo ácido, entre otros). Por otro lado, en el contexto de los sistemas híbridos, los equipos BESS pueden ser considerados una tecnología viable para estudios de resiliencia. Incluso, si a futuro se consideran los beneficios o sinergia positiva de la complementariedad (PV + BESS) para mejorar la resiliencia de los sistemas eléctricos se podrían desplazar los generadores diésel del portafolio óptimo de inversión, para mejorar la resiliencia de las redes de distribución frente a eventos HILP [5].

Figura 1: Nuevo marco conceptual de transición energética y resiliente en redes eléctricas 

Entre los diferentes eventos HILP de origen natural, los terremotos y las erupciones volcánicas son impredecibles y tienen efectos devastadores en las redes eléctricas. Al realizar una revisión de la literatura técnica especializada es acotado el número de publicaciones referente a la evaluación del impacto de las erupciones volcánicas en las redes eléctricas [6]-[8]. Dentro de los peligros volcánicos, las caídas de ceniza pueden provocar una interrupción del suministro de energía causada por descargas disruptivas de los aisladores debido a la acumulación de ceniza, mientras que los lahares (flujos de lodo y escombros) son más destructivos, causando daños considerables en postes eléctricos y líneas eléctricas aéreas [9]. Por ejemplo, según [10], la erupción del Volcán Fuego en Guatemala causó daños al sistema eléctrico en 2018 por el descenso de lahares y flujos piroclásticos, que afectaron al sistema de distribución de energía eléctrica. Las pérdidas económicas se calcularon en USD 1,04 millones, con cortes de energía que ocurrieron en 9 comunidades y afectaron a 3.705 clientes durante al menos dos días. Otro evento volcánico reciente fue la erupción del volcán Cordón Caulle en Chile que provocó continuos cortes de energía y apagones que afectaron alrededor del 40% de las ciudades cercanas durante al menos un mes [11].

Ecuador es un país permanentemente amenazado por este tipo de desastres debido a que está situado en el cinturón de fuego del Pacífico, que se caracteriza por concentrar algunas de las zonas de subducción más importantes del mundo, lo que ocasiona una intensa actividad sísmica y volcánica en las zonas que abarca. Por ejemplo, a partir de julio del 2015 el volcán Cotopaxi presentó una actividad inusual y peligrosa. La peligrosidad del volcán Cotopaxi radica en que sus erupciones pueden dar lugar a la formación de enormes lahares. Es importante mencionar que, las infraestructuras eléctricas de las provincias de Pichincha y Cotopaxi son más vulnerables debido a la ruta de descarga de los lahares [12].

Las autoridades del sector eléctrico ecuatoriano han puesto en marcha varias acciones con el objetivo de mitigar las afectaciones ante el probable evento eruptivo del volcán Cotopaxi. Entre las medidas tomadas se encuentran: la instalación de una subestación eléctrica móvil de 16-20 MVA, 69/13.8 kV en el cantón Salcedo, además se crearon proyectos de prevención para reforzar las redes del sistema de transmisión y distribución de las zonas amenazadas por lahares [12]. Adicionalmente, se complementó el plan de contingencia con la adquisición de centrales termoeléctricas móviles por parte de la empresa de distribución de Cotopaxi para garantizar un suministro continuo de energía eléctrica ante cualquier emergencia o desastre natural [13]. Sin embargo, los planes de contingencia establecidos por las diferentes empresas de distribución del país pueden no ser totalmente suficientes para restablecer la continuidad del servicio eléctrico de forma inmediata. De hecho, las acciones de respaldo ante eventos eruptivos expuestas en los planes de las empresas pueden tardar varias horas o inclusive días para ser aplicadas y garantizar nuevamente la seguridad y calidad del suministro eléctrico.

Por lo expuesto, se torna relevante determinar una planificación y operación óptima del sistema de distribución, de tal forma que mejore los índices de seguridad de suministro energético, y además que contribuya a la transición energética hacia el carbono neutralidad, con la finalidad de así desarrollar redes eléctricas de distribución resilientes frente a desastres naturales. En este sentido, el presente trabajo propone un marco metodológico para determinar la ubicación y dimensionamiento óptimo de DERs con el objetivo de mejorar la resiliencia de los sistemas de distribución frente a la ocurrencia de lahares volcánicos. Adicionalmente, se consideran los recursos de respaldo (generador móvil) para la etapa de restauración del sistema, de acuerdo a los planes de contingencia de las empresas de distribución.

El artículo está conformado por las siguientes secciones: En la sección 2 se propone una metodología para evaluar el impacto de los DERs en la resiliencia del sistema de distribución frente a la ocurrencia de lahares. En la sección 3 se describe el caso de estudio, y en la sección 4 se presentan el análisis de resultados. Por último, en la sección 5 se presentan las conclusiones y se proponen los posibles trabajos futuros de investigación.

METODOLOGÍA

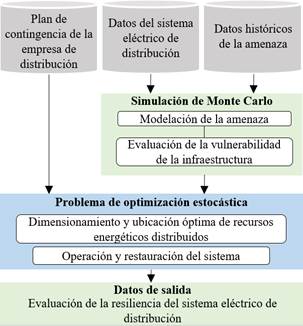
El marco metodológico propuesto para la planificación de recursos energéticos distribuidos en los sistemas de distribución de energía eléctrica y la evaluación de su impacto en la resiliencia del sistema frente a la ocurrencia de lahares volcánicos se ilustra en la Fig. 2. La metodología propuesta presenta dos etapas principales. La primera etapa incluye el método de simulación de Monte Carlo para la modelación de la amenaza y la evaluación de su impacto en la infraestructura del sistema de distribución (subestaciones y postes eléctricos de hormigón armado) mediante curvas de vulnerabilidad. En la segunda etapa se formula y resuelve un problema de optimización estocástica para determinar el dimensionamiento y la ubicación óptima de los recursos energéticos distribuidos resolviendo un DC-OPF (del inglés Direct Current-Optimal Power Flow), en el cual se incorpora un modelo de pérdidas linealizado y se incluyen los escenarios de contingencia obtenidos del método de simulación de Monte Carlo. Además, se reconoce la infraestructura existente en el plan de contingencia de la empresa de distribución para la etapa de restauración del sistema. Es importante destacar que, aunque el marco metodológico y la formulación propuestos se utilizan para lahares volcánicos, también pueden ser usados para evaluar otro tipo de amenazas naturales. A continuación, se presenta en detalle la metodología propuesta.

Datos de entrada

Sistema eléctrico de distribución

El sistema eléctrico de distribución se representa como un grafo G=(Ω_B, Ω_L), donde Ω_B denota el conjunto de nodos y Ω_L representa las líneas aéreas de distribución.

Datos históricos de erupciones volcánicas

Los datos históricos utilizados como datos de entrada están formados por las rutas históricas de descargas de lahares, además se consideran diferentes velocidades y densidades resultantes de la información vulcanológica actualizada generada y recopilada durante los últimos años [14].

Debido a la vulnerabilidad que presentan los sistemas eléctricos de distribución ante eventos HILP, las empresas de distribución se ven en la necesidad de elaborar e implementar planes de contingencia para mitigar los efectos de estos eventos, minimizando el impacto socio-económico que podría derivarse de los mismos; es por ello que se efectúan inversiones en la adquisición de infraestructura eléctrica, por ejemplo subestaciones y generadores móviles, para garantizar el suministro continuo de energía durante y después del evento. La metodología propuesta reconoce como datos de entrada la infraestructura eléctrica existente para enfrentar la contingencia.

Figura 2: Marco metodológico propuesto 

Simulación de Monte Carlo

Con el propósito de caracterizar la amenaza se generan varios escenarios utilizando el método de simulación de Monte Carlo, en este caso particular, para modelar los lahares volcánicos se consideran dos niveles de incertidumbre (la velocidad v_L y la densidad ρ_L) para determinar la presión dinámica (PD) de los flujos del lahar. La PD se determina usando la ecuación (1). Los datos utilizados como entrada comprenden diferentes velocidades, densidades y mapas de riesgo (ruta de descarga de lahar) obtenidos de eventos volcánicos históricos.

La probabilidad de daño de las subestaciones y postes de hormigón armado se determina mediante curvas de vulnerabilidad. En este trabajo, las curvas de vulnerabilidad representan la probabilidad de exceder un estado de daño de los elementos del sistema en función de la PD. Las curvas de vulnerabilidad se caracterizan por representaciones estadísticas y análisis de grandes conjuntos de datos sobre registros de fallas de diferentes elementos estructurales. En [15], se presentan datos del daño estructural causado por flujos volcánicos (piroclásticos y lahares) inferidos de los efectos de las armas nucleares, en donde diferentes elementos estructurales se evalúan en términos probabilísticos en función de PD. En este contexto, basados en [15], se infieren las curvas de vulnerabilidad aproximadas de los postes de hormigón de concreto armado y subestaciones. Las curvas de vulnerabilidad se ilustran en la Fig. 3.

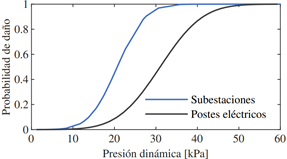
Figura 3: Curvas de vulnerabilidad de subestaciones y postes eléctricos de hormigón armado contra lahares 

Una vez obtenida la probabilidad de daño para los elementos vulnerables del sistema eléctrico, se establecen algunos supuestos para obtener su indisponibilidad para cada escenario de contingencia. Estos supuestos se describen a continuación: i) los nodos (subestaciones y postes de hormigón de concreto armado) no estarán disponibles si la probabilidad de daño es mayor que un umbral de probabilidad establecido. ii) si un nodo no está disponible, todas las líneas de distribución asociadas a ese nodo se consideran indisponibles. iii) los tiempos de recuperación para los diferentes elementos no disponibles del sistema se identifican con base en el conocimiento del operador del sistema de distribución, considerando la secuencia de cargas críticas que deben ser reconectadas a la red principal.

Utilizando el método de simulación de Monte Carlo y considerando los supuestos descritos anteriormente, se obtienen las matrices de indisponibilidad de nodos (ϛ_s,t,i) y líneas aéreas de distribución ((_s,t,ij). Esta etapa se implementó en el software M^{ATLAB R2019}a.

Datos de salida

El desempeño de los sistemas eléctricos se puede medir utilizando diferentes métricas [16]. Dos métricas detalladas en (2) y (3) han sido ampliamente utilizadas en estudios de confiabilidad y adoptadas en estudios de resiliencia. La primera métrica es la EENS (del inglés Expected Energy Not Supplied) durante el horizonte de evaluación, que está sujeto a la probabilidad de ocurrencia (π_s) de cada escenario de contingencia generado por la simulación de Monte Carlo. La segunda métrica está asociada al índice de falta de confiabilidad de la energía (EIU, del inglés Energy Index of Unreliability), que representa la relación entre la EENS y la demanda de energía (E) durante el horizonte de evaluación. Por lo tanto, si el índice es 0%, representa una cantidad de energía no suministrada nula, mientras que, si el índice es 100%, indica que no se suministró la demanda de energía del sistema.

FORMULACIÓN DEL PROBLEMA DE OPTIMIZACIÓN

Función objetivo

La función objetivo mostrada en la ecuación (4) y extendida en las ecuaciones (5) y (6) minimiza los CI en la capacidad instalada de sistemas PV ( P i 𝑷𝑽, 𝒊𝒏𝒔𝒕 ) y BESS ( 𝑷 𝒊 𝑩, 𝒊𝒏𝒔𝒕 ) en los nodos del sistema de distribución (N_B) donde, FRC es el factor de recuperación de capital, c^PV y c^B representan los costos por kW instalado. Además, la función objetivo minimiza los costos de operación (CO) que están sujetos a la probabilidad de ocurrencia (π_s) de cada escenario de contingencia (s) generado por el método de simulación de Monte Carlo. Los costos de operación incluyen, el valor de pérdida de carga VoLL (del inglés, Value of Lost Load), el costo de vertimiento de energía desde el sistema PV (c^PV,vert), el costo de la energía suministrada desde la red principal (c^red) y finalmente el costo del combustible asociado al consumo del generador móvil (c^comb). Es importante señalar que Ts es el horizonte de evaluación.

Restricciones del flujo de potencia óptimo en DC

Las ecuaciones (7)-(15) representan las restricciones asociadas al modelo DC-OPF propuesto en [17]. La ecuación (7) modela la primera ley de Kirchhoff de equilibrio de potencia activa de entrada y salida en cada nodo del sistema, donde 𝑷 𝒔,𝒕,𝒊 𝑳𝒊𝒏𝒆𝒂 representa el flujo de potencia de las líneas del sistema de distribución, 𝑷 𝒔,𝒕,𝒊 𝑷𝒆𝒓𝒅 representa el modelo linealizado de pérdidas nodales del sistema, 𝑷 𝒔,𝒊 𝑮𝑻 corresponde a la inyección de potencia del generador móvil, 𝑷 𝒔,𝒕,𝒊 𝑩,𝒄 y 𝑷 𝒔,𝒕,𝒊 𝑩,𝒅 representan la potencia de carga y descarga de los equipos de almacenamiento BESS, respectivamente; 𝑷 𝒔,𝒕,𝒊 𝑷𝑽 representa la potencia activa inyectada de los sistemas PV, 𝑷 𝒔,𝒕,𝒊 𝒓𝒆𝒅 representa la inyección de potencia activa de la red principal, 𝑫 𝒊,𝒕 y 𝑬𝑵𝑺 𝒔,𝒕,𝒊 corresponden a la demanda del sistema y la energía no suministrada (ENS), respectivamente. Además, se incluyen el parámetro 𝝆 𝒊 con el que se establece la ubicación del nodo en donde se encuentra la subestación y el parámetro 𝝉 𝒊 con el que se habilita la instalación de los DERs únicamente en los nodos de carga.

La ecuación (8) representa la restricción de la ENS relacionada con la demanda del sistema. La ecuación (9) representa la restricción de la capacidad de transferencia máxima de las líneas del sistema de distribución; en esta ecuación se incluye el parámetro (s,t,ij el cual representa la indisponibilidad de las líneas del sistema. La ecuación (10) modela la segunda ley de Kirchhoff basándose en la técnica disyuntiva big-M, donde M es una constante positiva suficientemente grande. Esta técnica (big-M) permite desacoplar los ángulos de tensión del bus asociado a las líneas de distribución que se desconectan debido a una contingencia en el sistema de distribución. Además, permite cumplir fácilmente con la segunda ley de Kirchhoff únicamente para las líneas de distribución disponibles para operar el sistema en los diferentes escenarios de contingencia.

Aproximación lineal de pérdidas nodales

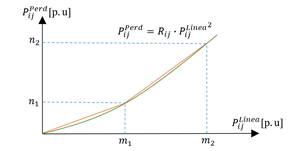
Las pérdidas nodales se presentan en la ecuación (11), la cual es una función cuadrática de los flujos de potencia en las líneas ( 𝑷 𝒔,𝒕,𝒊𝒋 𝑳𝒊𝒏𝒆𝒂 𝟐 ) multiplicada por la resistencias de las líneas ( 𝑹 𝒊𝒋 ) asociadas a un nodo i [18]. Para linealizar la ecuación cuadrática se aplica el método de linealización por tramos, empleando un conjunto especial ordenado de variables de tipo 2 (SOS2, del inglés Special Ordered Set), donde se debe cumplir que el conjunto de variables puedan tomar valores reales entre cero y uno, en el que no más de dos miembros adyacentes sean distintos de cero en una solución factible [19]. La ecuación (12), representa la linealización del flujo de potencia de las líneas ( 𝑷 𝒔,𝒕,𝒊𝒋 𝑳𝒊𝒏𝒆𝒂 ). La ecuación (13), representa las pérdidas nodales linealizadas ( 𝑷 𝒔,𝒕,𝒊 𝑷𝒆𝒓𝒅 ). En este grupo de ecuaciones 𝜷 𝒔,𝒕,𝒊𝒋,𝒑 corresponde al grupo de variables SOS2 que deben cumplir con la restricción (14). Por otro lado, 𝒎 𝒑 y 𝒏 𝒑 representan los puntos de quiebre de la linealización como se puede ver en la Fig. 4. Finalmente, debido a la función cuadrática de las pérdidas nodales, se debe cumplir la restricción de los puntos de quiebre mostrada en la ecuación (15).

Figura 4: Aproximación lineal de pérdidas nodales 

Restricciones del sistema fotovoltaico

La inyección de potencia activa esperada de un sistema PV ( 𝑷 𝒔,𝒕,𝒊 𝑷𝑽 ) se expresa mediante las ecuaciones utilizadas en [20]. La inyección de potencia (16) es función de la potencia instalada del sistema ( 𝑷 𝒊 𝑷𝑽,𝒊𝒏𝒔𝒕 ), irradiación solar ( 𝑰 𝒔,𝒕 ), la temperatura de las celdas solares ( 𝑻 𝒔,𝒕 𝑷𝑽 ), la reducción de la eficiencia del sistema PV debido a la temperatura ( 𝜼 𝑻 ), la eficiencia del inversor ( 𝜼 𝑷𝑽,𝒊𝒏𝒗 ) y el vertimiento de energía del sistema ( 𝑷 𝒔,𝒕,𝒊 𝑷𝑽,𝒗𝒆𝒓𝒕 ). La temperatura de las celdas solares se representada en la ecuación (17), esta depende de la irradiación solar, la temperatura ambiente ( 𝑻 𝒔,𝒕 𝒂 ) y la temperatura del sistema PV en condiciones normales (NOCT, del inglés Normal Operating Cell Temperature). La ecuación (18) restringe la capacidad de potencia instalada del sistema PV y habilita únicamente a cada nodo no vulnerable del sistema de distribución para ser candidato a instalar un sistema PV.

Restricciones del sistema de almacenamiento de energía en base a baterías

La inyección de potencia activa de los sistemas de almacenamiento BESS se expresa mediante las ecuaciones utilizadas en [21] y [22]. Las ecuaciones (19) y (20) definen la cantidad de energía disponible en los BESS. La restricción (19) representa la cantidad de energía inicial de los BESS ( 𝑬 𝒔,𝒕=𝟎,𝒊 ), en el que ( 𝑺𝑶𝑪 𝟎 ) es el estado inicial de carga de los BESS. La ecuación (20) define la cantidad de energía disponible ( 𝑬 𝒔,𝒕,𝒊 ) para un horizonte de evaluación considerando la carga 𝑷 𝒔,𝒕,𝒊 𝑩,𝒄 y descarga 𝑷 𝒔,𝒕,𝒊 𝑩,𝒅 de los BESS además de la eficiencia del inversor 𝜼 𝑩,𝒊𝒏𝒗 . La ecuación (21) restringe la energía de la batería que es limitado por la potencia instalada del BESS ( 𝑷 𝒊 𝑩, 𝒊𝒏𝒔𝒕 ), además habilita únicamente a los nodos no vulnerables al evento exógeno para instalar unidades BESS. Las restricciones (22)-(24) indican que los BESS únicamente puede operar en estado de carga o descarga en cada hora del horizonte de simulación, representado por las variables binarias 𝝌 𝒔,𝒕,𝒊 𝒄 y 𝝌 𝒔,𝒕,𝒊 𝒅 , respectivamente, donde M es una constante positiva suficientemente grande que habilita que las variables 𝑷 𝒔,𝒕,𝒊 𝑩,𝒄 y 𝑷 𝒔,𝒕,𝒊 𝑩,𝒅 obtengan valores distintos a cero en función del estado de funcionamiento de los BESS.

Restricciones del generador móvil

El modelo de generadores térmicos propuesto en [23] es considerado para este trabajo, el cual es modelado por las ecuaciones (25) y (26). La ecuación (25) corresponde el consumo de combustible ( 𝒇 𝒔,𝒕 𝒄𝒐𝒎𝒃 ), donde 𝑷 𝒔,𝒊 𝑮𝑻 es la energía suministrada por el generador móvil, 𝒖 𝑮𝑻 es el poder calorífico del combustible en kWh/kg, y 𝜼 𝑩,𝒊𝒏𝒗 es la eficiencia del generador térmico. La restricción (26) representa el límite de suministro de energía del generador térmico, además se incluye la variable binaria 𝝌 𝒊 que representa la instancia del generador en un nodo i, con esto se logra una ubicación óptima del generador móvil en el sistema de distribución.

CASO DE ESTUDIO

La metodología propuesta se implementa en el alimentador de la subestación San Rafael ubicada en Sangolquí, Ecuador. Para este estudio, se utilizan curvas representativas de irradiación solar diaria de invierno y verano en diferentes horas del día (6:00, 14:00 y 22:00) obtenidas de [24], con el objetivo de determinar el impacto de la ocurrencia de una erupción volcánica bajo diferentes niveles de irradiación solar. Además, se restringe la capacidad máxima instalada de los sistemas PV según la REGULACIÓN Nro. ARCERNNR-001/2021 denominada "Marco normativo de la Generación Distribuida para autoabastecimiento de consumidores regulados de energía eléctrica", disponible en [25]. Los costos por kW instalado del sistema PV y BESS (tecnología ion-litio) son de 1000 USD/kW [26] y 500 USD/kW [27], respectivamente. Adicionalmente, se considera el plan estratégico ante emergencias de la empresa de distribución, en donde se establece la utilización de generadores móviles ante cualquier contingencia en el sistema; la capacidad del generador termoeléctrico asumida para este estudio es igual a la demanda punta del sistema (16.35 MVA), con el fin de visualizar la recuperación total del sistema. Por otro lado, se establece un VoLL diferente para cada tipo de carga en función de su tipo de carga. El VoLL definido para cargas industriales, de servicio y de emergencia es de 1,50 USD/kWh [28]. Para este estudio, el VoLL residencial se define en función de [29], además, la restricción presupuestaria se fija en 10 MMUSD y el FRC se calcula con un plazo de pago de 10 años a una tasa de interés del 15%.

Evento del lahar volcánico

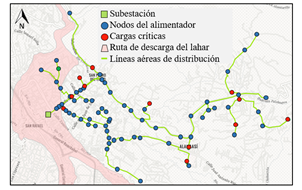
Los datos utilizados de velocidades y densidades para caracterizar los lahares del volcán Cotopaxi se obtuvieron a partir de modelos basados en la erupción histórica de 1877 [33], [34]. En la Fig. 5 se muestra el diagrama unifilar del alimentador San Rafael y la trayectoria del lahar formado desde el flanco norte del volcán Cotopaxi.

Con la información descrita anteriormente del sistema de distribución y del evento del lahar volcánico, se plantean dos casos de estudio. En el primero se propone un caso base que corresponde a la evaluación del sistema de distribución sin considerar la inversión de DERs, únicamente considera la ubicación óptima del generador móvil para la etapa de restauración del sistema. El segundo caso considera un portafolio de inversión basado en sistemas PV y dispositivos de almacenamiento BESS. Adicionalmente, se complementa la inversión con la ubicación óptima del generador móvil para la etapa de restauración.

Figura 5: Diagrama unifilar del alimentador San Rafael considerando los impactos y cargas críticas 

ANÁLISIS DE RESULTADOS

En la Tabla 1 se muestran los resultados obtenidos de la capacidad instalada de los DERs, el costo de inversión y la métrica EENS para los casos descritos anteriormente. Como se puede observar, el valor de la EENS para el caso base cuando no se considera la inversión de DERs es de 1,32 GWh, mientras que para el caso con inversión el valor de la EENS disminuye a 1,19 GWh, esto se debe a la contribución de los DERs instalados en la operación del sistema de distribución, que permiten reducir 0.13 GWh de EENS. Por otro lado, los costos esperados de operación y de consumo de combustible por parte del generador diésel durante la contingencia se reducen en un 37 % y 7% respectivamente.

Tabla 1:  Resultados de la capacidad instalada de DERs, costo de inversión y EENS 

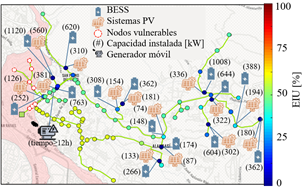
En la Fig. 6 se muestra la ubicación y capacidad instalada de los DERs y la localización del generador móvil en el sistema de distribución. Además, cada circulo representa los nodos del sistema y el color indica el porcentaje de EIU. Los resultados demuestran que la métrica EIU se reduce de un 45% a 0% para todas las cargas críticas del sistema cuando se considera la instalación de los DERs, asimismo en algunas cargas vecinas a las cargas críticas, la métrica EIU se reduce de un 45% alrededor de un 15%. Estos resultados de la métrica EIU muestran que los DERs son capaces de mejorar la resiliencia del sistema de distribución, enfocándose principalmente en el suministro de energía de cargas críticas, como hospitales y refugios de emergencia, los cuales son de vital importancia dado el impacto económico y social que pueden provocar los lahares luego de una posible erupción del volcán Cotopaxi.

Figura 6:  EIU del alimentador de San Rafael 

El mejoramiento de la resiliencia de las redes de distribución también se puede evaluar en términos de la capacidad de demanda suministrada, considerando las inversiones obtenidas de los DERs en el sistema de distribución durante el horizonte de evaluación. Las Fig. 7 y 8 muestran la demanda suministrada para tres escenarios considerados (donde la erupción ocurre a las 6:00, 14:00 y 22:00 horas del día), con niveles de irradiación solar de los meses de verano e invierno respectivamente. Es importante destacar que, en la etapa de restauración, en los tres escenarios evaluados el generador móvil se conecta 12 horas después de ocurrido el evento. Este supuesto es aplicado según diferentes planes de emergencia en donde se destaca que las cargas críticas del sistema no pueden estar sin suministro de energía por más de un tiempo límite (por ejemplo, hasta 12 horas) [35].

La Fig. 7 muestra los escenarios bajo estudio con niveles de irradiación de verano. El escenario de las 6:00 a.m. en donde los DERs pueden suministrar el 20% de la demanda luego de ocurrido el evento, sin embargo, al aumentar la disponibilidad del recurso solar a lo largo del día, la infraestructura planificada (PV+BESS) puede suministrar hasta un 25% de la demanda. Para el escenario de las 14:00 horas se suministra hasta un 25% de la demanda en la hora inicial del evento, sin embargo, durante el tiempo restante de la restauración, la capacidad de suministro de energía disminuye progresivamente debido a la reducción del recurso solar. Finalmente, para el escenario de las 22:00 horas se observa que el suministro de energía se mantiene constante en un 6%, para este caso al ocurrir el evento en la noche, únicamente se suministra energía al sistema por medio de los equipos de almacenamiento BESS. Por otro lado, la Fig. 8 muestra los escenarios bajo estudio con niveles de irradiación de invierno. La capacidad de suministro disminuye debido a una menor disponibilidad del recuso solar, no obstante, para los escenarios de las 6:00 y 14:00 horas los DERs pueden abastecer el 18% de la demanda una vez ocurrido el evento, mientras que en el escenario de las 22:00 horas el suministro de energía se mantiene constante en un 6%.

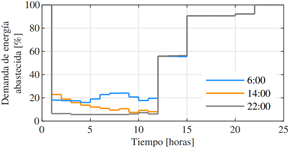
Figura 7:  Evolución de la capacidad por hora para satisfacer la demanda de energía eléctrica con niveles de irradiación solar de verano 

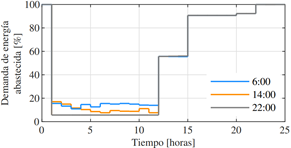
Figura 8:  Evolución de la capacidad por hora para satisfacer la demanda de energía eléctrica con niveles de irradiación solar de invierno 

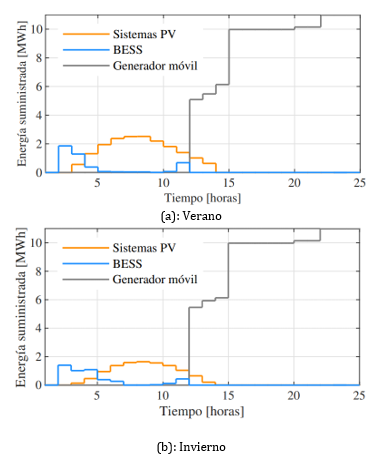
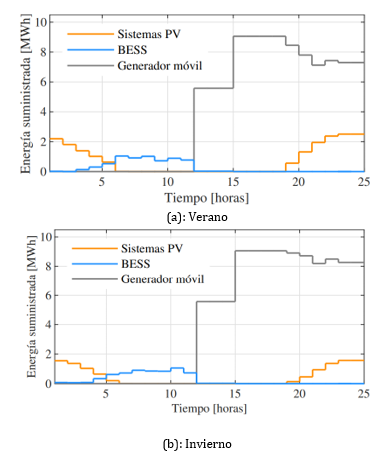
En la Fig. 9 se muestra el suministro de energía por medio de los DERs y del generador móvil para el escenario en donde el evento ocurre a las 6:00 horas con niveles de irradiación de verano (ver Fig. 9(a)) y de invierno (ver Fig. 9(b)). Como se puede observar en las horas iniciales después de ocurrido el evento, al no contar con disponibilidad de recurso solar, el suministro de energía se realiza por medio de BESS, sin embargo, al tener mayor irradiación solar, la demanda es suministrada progresivamente por los sistemas PV. En la hora 11, luego de ocurrido el evento, la demanda vuelve a ser suministrada por los BESS debido a la disminución del recurso solar. Es importante destacar que, tanto en el escenario de invierno y verano, a partir de la hora 12 luego de ocurrido el evento se conecta el generador móvil para restaurar el suministro del sistema, sin embargo, al contar con sistemas PV instalados en la red, el suministro de energía del generador móvil durante la contingencia disminuye debido a que los sistemas PV permiten reducir los costos de operación durante la contingencia.

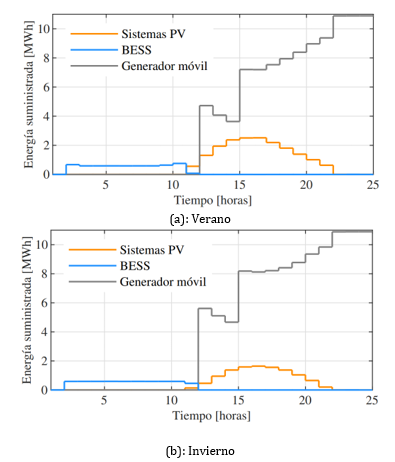
En la Fig. 10 se muestra el suministro de energía por medio de los DERs y del generador móvil para el escenario en donde el evento ocurre a las 14:00. Como se puede observar, en el periodo comprendido entre las 0 y 6 horas después de ocurrido el evento, al contar con disponibilidad de recurso solar, el suministro de energía se realiza por medio de los sistemas PV. Además, mientras los niveles de irradiación solar disminuyen los BESS suministran energía progresivamente hasta la hora 12, donde se conecta el generador móvil para restaurar el suministro del sistema, al mismo tiempo se visualiza que la participación del generador móvil en el suministro de energía, depende de la disponibilidad del recurso solar, por lo tanto en los escenarios con niveles de irradiación de verano (ver Fig. 10(a)) el generador móvil tiene una menor participación en el suministro que en los escenarios de irradiación de invierno (ver Fig. 10(b)).

Figura 9:  Suministro de energía para el escenario de ocurrencia del evento a las 6:00 horas 

Figura 10:  Suministro de energía para el escenario de ocurrencia del evento a las 14:00 horas 

En las Fig. 11(a) y Fig. 11(b) se muestra el suministro de energía por medio de los DERs y del generador móvil para el escenario en donde el evento ocurre a las 22:00 horas con niveles de irradiación de verano e invierno, respectivamente. Como se puede observar en el periodo comprendido entre las 0 y 12 horas después de ocurrido el evento, al no contar con disponibilidad de recurso solar, el suministro de energía se realiza por medio de BESS. A partir de la hora 12 se conecta el generador móvil para restaurar el suministro del sistema, sin embargo, al tener sistemas PV instalados en la red, la contribución del generador móvil al suministro de energía durante la contingencia disminuye.

Figura 11:  Suministro de energía para el escenario de ocurrencia del evento a las 22:00 horas 

Por lo tanto, se puede concluir que los DERs planificados son capaces de mejorar la resiliencia del sistema ante la ocurrencia de lahares volcánicos, suministrando energía a cargas críticas. Además, es importante señalar que, el modelo es capaz de dimensionar y localizar los equipos DERs con el propósito de cumplir con el objetivo de mejorar la resiliencia del sistema en diferentes escenarios de ocurrencia del evento exógeno con distintos niveles de irradiación solar, en donde los DERs desplazan los generadores móviles debido a sus bajos costos de operación.

CONCLUSIONES

En el presente trabajo se propone una metodología para determinar el dimensionamiento y la ubicación óptima de recursos energéticos distribuidos considerando sistemas PV y BESS, con el objetivo de mejorar la resiliencia del sistema de distribución frente a la ocurrencia de desastres naturales, en este caso particular se evalúa la ocurrencia de lahares volcánicos.

La metodología propuesta se aplica en el alimentador San Rafael ubicado en Sangolquí, Ecuador. Los resultados obtenidos demuestran que, mediante la inversión en DERs es posible reducir hasta un 45% de EIU en las cargas críticas, así se demuestra que la metodología propuesta permite mejorar la resiliencia de las redes de distribución frente a la ocurrencia de lahares. Esta metodología prioriza el suministro de energía de cargas críticas como refugios de emergencia, centros de salud comunitarios, entre otros, los que son de vital importancia para poder enfrentar la contingencia y mitigar los efectos socio-económico que causan en la población.

La propuesta es una herramienta práctica que podría ser utilizada por planificadores y operadores de las empresas de distribución para determinar un plan de prevención óptimo mediante la instalación de sistemas PV y BESS que permita fortalecer las redes de distribución en las zonas amenazadas por desastres naturales.