INTRODUCCIÓN
Los sistemas eléctricos de potencia tienen como objetivo principal brindar un servicio eléctrico de calidad al consumidor final al menor costo posible. Para lograr este objetivo es necesario realizar análisis y estudios los cuales son la base de una correcta planificación y operación de los sistemas eléctricos. Dichos análisis y estudios se fundamentan principalmente en una serie de simulaciones en software con la finalidad de representar fielmente el comportamiento de los sistemas reales. La veracidad de estas simulaciones depende fuertemente de la precisión de los modelos eléctricos de los diversos componentes físicos del sistema [1].
Entre los componentes que deben ser modelados se encuentran las cargas. Prácticamente todos los estudios se ven influenciados por los modelos de carga, algunos ejemplos son: estudios y aplicaciones que evalúan la estabilidad de tensión, ángulo o frecuencia [1]-[5]; estudios de despacho económico [6]; ajuste de protecciones, localización de fallas, tiempo de despeje de fallas [7], [8]; localización y dimensionamiento óptimo de capacitores y generación distribuida [9], [10]; flujo de potencia óptimo [11]; entre muchos otros [12].
A diferencia del modelamiento de otros componentes del sistema, como generadores o líneas, la carga es uno de los elementos más desafiantes de modelar ya que sus modelos y parámetros varían continuamente con el tiempo, el clima, la geografía, la evolución tecnológica y con diferentes incertidumbres propias de los consumidores, tal es así que varían hasta con situaciones mundiales extraordinarias como la pandemia de COVID-19 [13], [14].
Aunque el modelamiento de carga ha sido ampliamente estudiado y documentado en el pasado, en los últimos años ha resurgido un gran interés en su investigación. Algunos motivos son: el crecimiento continuo de las redes, nuevas interconexiones, operación cerca de los límites de estabilidad, generación distribuida, almacenamiento, nuevas tecnologías de la carga especialmente a base de electrónica, entre otros. Todo esto obliga a realizar estudios y aplicaciones cada vez más sofisticados para planificar y operar correctamente el sistema. Estos estudios y aplicaciones necesitan modelos de carga cada vez más precisos y a la vez representativos de una mayor cantidad de escenarios de operación, de hecho, algunos estudios requieren series temporales de modelos de carga [15] y algunas aplicaciones (en tiempo real) requieren modelos de carga estimados continuamente en el tiempo [4].
En base a todo lo descrito hasta aquí, es evidente la importancia del modelamiento de carga y el interés actual en su investigación. Es por esto que este trabajo presenta una revisión bibliográfica sobre modelamiento de carga en sistemas eléctricos de potencia. El trabajo se organiza de la siguiente manera: en la sección 2 se desarrolla un breve marco teórico sobre modelamiento de carga; en la sección 3 se propone una metodología de clasificación bibliográfica enfocada específicamente hacia el modelamiento de carga; en la sección 4 se presentan las tendencias actuales de investigación, las áreas poco investigadas, se describen varias propuestas de investigación y finalmente se determinan los campos futuros de investigación. En la quinta y última sección se exponen las conclusiones.
Aunque en la literatura existen revisiones bibliográficas actuales al respecto, como [16], [17], a criterio y conocimiento de los autores este trabajo tiene las siguientes ventajas: i) se presenta la primera metodología sistemática de clasificación bibliográfica enfocada específicamente al modelamiento de carga; ii) es la primera revisión bibliográfica que deduce metódicamente las tendencias actuales y las áreas poco investigadas, y; iii) este trabajo prioriza las investigaciones de la última década para determinar las tendencias actuales y nichos futuros de investigación.
MARCO TEÓRICO
El modelamiento de carga es una tarea que permite modelar adecuadamente las cargas de un sistema eléctrico con el fin de representar correctamente su funcionamiento en diferentes estudios o aplicaciones. La tarea del modelamiento de carga abarca principalmente dos etapas: i) la elección de un modelo de carga y, ii) la identificación paramétrica de los parámetros/constantes del modelo de carga elegido [14].
Modelos de Carga
Los modelos de carga son funciones matemáticas que intentan reproducir el comportamiento real de las cargas. Estas funciones tienen como variable de salida a la potencia activa o reactiva. Las variables independientes suelen ser: la tensión, la frecuencia y/o el tiempo.
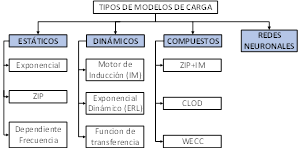
Los modelos de carga se clasifican en: estáticos, dinámicos, compuestos y redes neuronales artificiales (ANN). En la literatura existe una gran cantidad de modelos de carga. Los más utilizados se observan en la Fig. 1. Dado que los modelos de carga se encuentran bien documentados en [2], [5], [14], [18], en este trabajo no se los desarrolla.
Identificación Paramétrica
La identificación paramétrica es el proceso que permite determinar el valor de los parámetros de los modelos de carga, de tal manera que, al ajustar dichos parámetros, los modelos de carga reproduzcan fielmente el comportamiento real de las cargas. Este proceso puede ser realizado desde dos enfoques, uno basado en componentes y otro basado en mediciones.
Enfoque de componentes
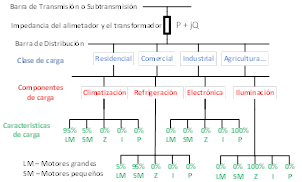
Este enfoque se fundamenta en el conocimiento de las cargas, es decir, en conocer los equipos, aparatos, electrodomésticos, etc., conectados a una red. Dado que actualmente es imposible conocer todas estas cargas, ya sea en un punto fijo de tiempo o más aún a lo largo del tiempo, el enfoque propone agrupar las cargas en componentes o usos finales típicos (climatización, iluminación, etc.) y estos a su vez en clases típicas de consumidores (residencial, comercial, etc.), ver Fig. 2. La idea es determinar las cargas típicas que conforman cada componente y los componentes típicos que conforman cada clase (generalmente se obtienen de encuestas) en uno o pocos puntos de una red. En base a estos pocos puntos se estiman o extrapolan los modelos de carga de otros nodos o barras [14], [18].
Las principales ventajas de este enfoque son: correlación entre los modelos utilizados y las cargas físicas; las clases de carga en una subestación están generalmente disponibles (de la facturación); no requiere mediciones; es aplicable a diferentes sistemas y condiciones; entre otras. Las principales desventajas son: el modelo obtenido asume que la estructura y composición no cambia con el tiempo, el clima, la geografía o el comportamiento del cliente; se obtienen, como máximo, modelos para un reducido número de escenarios; dificultad y esfuerzos considerables en la realización de encuestas; la composición de cada clase puede cambiar sustancialmente en cada alimentador o barra; entre otras [14], [18].
Enfoque de mediciones
Este enfoque se sustenta en mediciones obtenidas por equipos de campo. Se parte de la disponibilidad de mediciones de tensión, frecuencia, potencia activa P y reactiva Q. La idea es seleccionar un modelo de carga, aplicarle las mediciones de tensión y frecuencia, obtener su respuesta de P y Q, comparar esta respuesta con las mediciones reales (P y Q) a través de una función objetivo y, finalmente, minimizar el error de esta función mediante una técnica de optimización que ajuste los parámetros del modelo de carga [14], [18].
Las ventajas de este enfoque son: mayor simplicidad con respecto al enfoque de componentes; puede capturar los cambios temporales de la carga si existen suficientes mediciones; es aplicable a cualquier carga; no es necesario conocer las características de las cargas, entre otras. Las principales desventajas son: necesidad de una gran cantidad de mediciones para obtener un modelo confiable; necesidad de perturbaciones de gran magnitud para identificar correctamente ciertos parámetros de los modelos; no se puede inducir perturbaciones de gran magnitud; dificultad de obtener mediciones durante grandes perturbaciones; limitaciones en las técnicas de optimización para identificar gran cantidad de parámetros de modelos de carga complejos; entre otros [14], [18].
METODOLOGÍA DE CLASIFICACIÓN BIBLIOGRÁFICA
En la bibliografía se han encontrado diferentes metodologías y propuestas para modelar la carga, sin embargo, no se han encontrado formas o criterios para clasificar y evaluar dichas propuestas. Como solución, en este trabajo se ha escogido una metodología de clasificación bibliográfica basada en características [19] la cual consta de los siguientes seis pasos: i) se revisa (lectura y comprensión superficial) varios artículos científicos de la bibliografía; ii) se identifica una serie de características trasversales al modelamiento de carga que permitan determinar las tendencias actuales y las áreas poco investigadas; iii) se clasifica cada artículo científico de la bibliografía de acuerdo a las características predefinidas; iv) se identifican las tendencias actuales y áreas poco investigadas de acuerdo a la clasificación bibliográfica del punto anterior; v) se analizan con mayor detalle los artículos científicos que se consideren de interés y; vi) se definen los nichos futuros de investigación.
En esta sección se detallan los tres primeros pasos de la metodología de clasificación bibliográfica. Siete características transversales al modelamiento de carga se han identificado (ver Tabla 1); estas son:
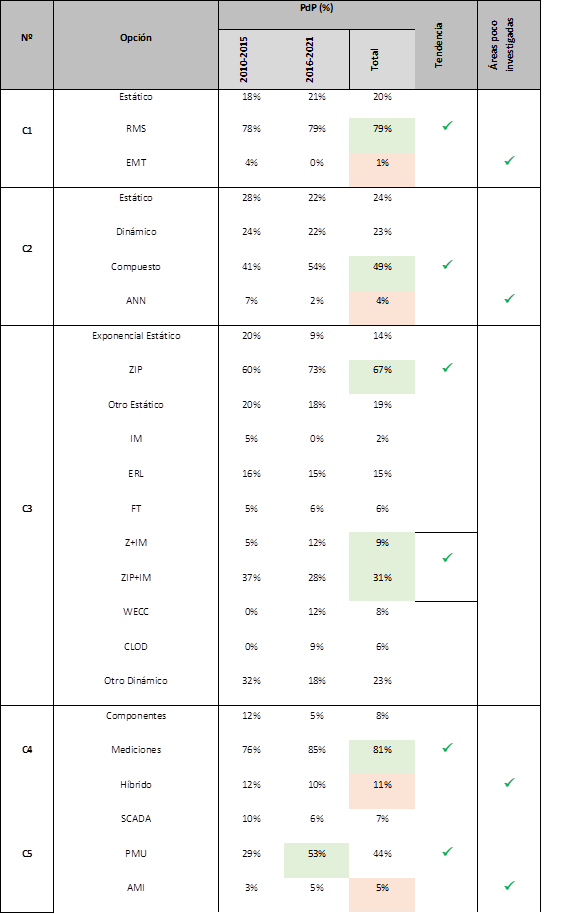
C1 » Tipo de estudio.- Indica si la propuesta se enfoca en estudios: estáticos, dinámicos RMS (análisis de transitorios electromecánicos) y/o dinámicos EMT (análisis de transitorios electromagnéticos). Ver Tabla 1.
C2 » Tipo de modelo de carga.- Indica si el artículo científico se enfoca o utiliza modelos de carga: estáticos, dinámicos, compuestos y/o redes neuronales artificiales (ANN). Ver Tabla 1.
C3 » Especifica el modelo de carga: exponencial estático, ZIP, otro estático; motor de inducción (IM), exponencial dinámico (ERL), función de transferencia (FT), Z+IM (impedancia constante + motor de inducción), ZIP+IM, WECC (modelo desarrollado por “Western Electricity Coordinating Council” en [5]), CLOD (modelo adoptado por el programa “Power System Simulator for Engineering (PTI PSS/E)” de Siemens), y/u otro modelo dinámico de carga. Ver Fig. 1 y Tabla 1.
C4 » Tipo de identificación paramétrica que utiliza o propone el artículo científico. Las opciones son: enfoque de componentes, mediciones o, híbrido.
C5 » Origen de datos.- Indica el origen de los datos utilizados en cada artículo científico: SCADA (Supervisión, Control y Adquisición de Datos), Unidades de Medición Fasorial (PMU), AMI (Infraestructura de Medición Avanzada) con sus medidores inteligentes, analizadores de calidad de energía, otros tipos de mediciones (ej. mediciones instantáneas), otros (encuestas, facturación, literatura, fabricantes, etc.); ver Tabla 1. Es importante destacar que varios artículos se basan en pseudomediciones provenientes de simulaciones, sin embargo, esta característica indica la tecnología que se utilizaría para la medición en sistemas eléctricos reales.
C6 » Tipos de mediciones.- Las mediciones que se utilizan para el proceso de identificación paramétrica pueden ser de: eventos, tipo ambiente o, de ambos; ver Tabla 1. La identificación paramétrica con eventos ajusta las variables de un modelo de carga solamente cuando existen registros de una perturbación de considerable magnitud (ej. fallas en líneas de transmisión). El modelamiento de carga con datos tipo ambiente utiliza los datos registrados continuamente en el tiempo, sin la necesidad de que ocurra un evento.
C7 » Tipo de ejecución.- Indica si la metodología de modelamiento de carga propuesta en cada artículo científico está pensada para ser ejecutada: fuera de línea (realizada generalmente de forma manual o semiautomática con mediciones o registros pasados), en línea (ejecutada automáticamente con datos que se actualizan continuamente en el tiempo) o, en tiempo real (igual a la anterior pero se ejecuta en tiempo real, es decir, en máximo un par de segundos). Ver Tabla 1.
De acuerdo a las siete características predefinidas se clasifican 62 artículos científicos; estos son: [23]-[84]. Es importante destacar que: i) la bibliografía data a partir del año 2010 y, ii) los artículos se enfocan en la identificación paramétrica de modelos de carga, mas no en investigaciones de nuevos o mejores modelos.
TENDENCIAS ACTUALES, ÁREAS POCO INVESTIGADAS Y CAMPOS FUTUROS DE INVESTIGACIÓN
A partir de la clasificación bibliográfica (62 trabajos antes mencionados) se calcula el Porcentaje de Publicaciones (PdP) por cada una de las siete características predefinidas. Adicionalmente, se desagrega este PdP para los periodos 2010-2015 y 2016-2021, tal como se observa en la Tabla 1. El objetivo es deducir las tendencias actuales y las áreas poco investigadas. A continuación, se las desarrolla junto con la descripción de algunas propuestas y los campos futuros de investigación.
Tipo de Estudio y Tipo de Modelo (C1 - C3)
De la primera fila (C1) de la Tabla 1 se observa que, desde el año 2010, la mayor cantidad de publicaciones se enfocan en estimar modelos de carga para simulación RMS (79%). De los modelos de carga acordes para simulación RMS (dinámicos, compuestos, ANN) los más adecuados son los modelos compuestos ya que, en la vida real, la carga está compuesta por cargas estáticas y dinámicas. Se constata que los modelos compuestos son la tendencia actual con 49% de PdP (fila C2 de la Tabla 1). Dentro de los modelos compuestos se observa que el más investigado es el ZIP+IM (fila C3 de la Tabla 1); el modelo Z+IM es un caso particular del ZIP+IM y juntos tienen un PdP de 40%. Los modelos de carga WECC y CLOD son menos estudiados debido a: su gran complejidad, dificultad en su implementación en programas de simulación que no los tengan implementados por defecto y, falta de transparencia de estos modelos hacia el usuario en los softwares comerciales. Como solución, en [20] se presenta la primera referencia abierta para desarrollar el modelo WECC en programas de simulación que no lo tengan implementado. Es importante mencionar que no hay un modelo de carga mejor que otro ya que se seleccionan de acuerdo al comportamiento que tienen la cargas en la vida real.
En cuanto a los modelos estáticos, la tendencia actual es la estimación de los parámetros del modelo ZIP. El 67% de los trabajos enfocados en modelos estáticos lo investigan. Es importante señalar que actualmente una gran cantidad de trabajos [9]-[12] y estudios eléctricos en estado estable incorporan la dependencia de la carga con la tensión mediante el modelo ZIP.
En [21] se presentan los modelos de carga utilizados por las industrias del sector eléctrico a nivel mundial en el año 2010. Para estudios estáticos, el 84% de modelos utilizados eran PQ constante y tan solo el 8% ZIP. Para estudios dinámicos, el 72% de modelos utilizados eran simplemente algún tipo de modelo estático. Sino se representa correctamente el comportamiento de la carga, sobre todo en simulación dinámica, los estudios pueden arrojar resultados erróneos. Se evidencia que las investigaciones de la última década (Tabla 1) atacan las falencias anteriores al año 2010.
Por otro lado, las áreas poco investigadas que se han identificado y que representan un campo futuro de investigación son:
Modelamiento de carga para simulación EMT. En [22] se demuestra que pueden existir problemas de inestabilidad a nivel subciclo cuando se tiene una gran cantidad de electrónica de potencia.
Redes neuronales artificiales (ANN) como modelos de carga. Solo el 4% de las publicaciones las estudian. La principal desventaja es la cantidad de información necesaria para entrenarlas y validarlas. Aunque actualmente se dispone de gran cantidad de mediciones (tensión, corriente, etc.), aún no se dispone de información verídica y continua de la composición, consumo y estructura de las cargas.
Las tendencias actuales y las áreas poco investigadas se sintetizan en las dos últimas columnas de la Tabla 1.
Tipo de Identificación Paramétrica (C4)
De la cuarta fila (C4) de la Tabla 1 se deduce claramente que la tendencia actual es estimar modelos de carga con identificación paramétrica en base a mediciones (81% de PdP). Esto era esperable por el gran despliegue de tecnologías de medición que ha habido en las últimas dos décadas.
En la literatura se han utilizado una gran cantidad de técnicas y metodologías de optimización. Algunas de las más utilizadas son: mínimos cuadrados, mínimos cuadrados no lineales y similares [23]-[31]; Levenberg-Marquardt [32], [33]; algoritmos genéticos [34]-[38]; optimización por enjambre de partículas [39], [40]; redes neuronales artificiales [41]-[43]; filtro de Kalman [44]; ajuste vectorial [45]; máquinas de soporte vectorial [46] y; árbol de decisiones [47].
Por otro lado, aunque el enfoque de componentes fue el más utilizado en el anterior siglo, en la última década ha disminuido considerablemente su utilización (5% en 2016-2021). A pesar de esto, en un futuro podría resurgir su uso debido a que hoy en día los registros de medidores inteligentes permiten determinar las clases de carga con mayor resolución. Además, en un futuro se espera que los sensores inalámbricos, los Sistemas de Gestión de Energía del Hogar (HEMS) y el Internet de las Cosas (IoT) permitan estimar la composición y estructura [85] de las cargas. En este sentido, un área poco investigada y que representa un campo futuro de investigación es la identificación paramétrica híbrida, tan solo tiene un PdP de 11%.
En [64] se presenta una metodología de modelamiento de carga con identificación paramétrica en base a componentes y hasta cierto punto con enfoque híbrido. Con datos de medidores inteligentes se agrupa a los consumidores con la técnica k-means; se asume que los usuarios con semejantes perfiles de carga tienen equipos y comportamientos similares. De cada grupo se selecciona un usuario prototipo al cual se le instala y realiza mediciones intrusivas a sus equipos por medio de sensores inalámbricos; estos se conectan mediante ZigBee o WiFi a un enrutador y este a su vez a un centro de datos en donde se calcula los componentes de carga de los usuarios típicos. Con identificación paramétrica basada en componentes se agrupa las cargas para obtener un modelo ZIP+IM en media o alta tensión. La principal desventaja de esta propuesta son las mediciones intrusivas.
En [50] se propone una metodología de modelamiento de carga en barras de transmisión de alta tensión (AT) con identificación paramétrica híbrida. Los datos de entrada son mediciones de PMU’s en la barra de AT y la composición de la carga (conectada aguas abajo en la barra de media tensión y en sus correspondientes alimentadores). La técnica Support Vector Machines (SVM) se utiliza para obtener y clasificar la carga de una barra en clases (residencial, comercial, etc.) con tres criterios: i) datos de la composición de la carga de cada clase obtenida de empresas distribuidoras; ii) luego de una perturbación, ciertos únicos modos oscilatorios se observan en cada clase y; iii) cuando se realiza el proceso de ajustar los parámetros de un modelo de motor de inducción (IM), con un modelo agregado IM por clase, los parámetros encontrados de cada clase son diferentes. Finalmente se determinan los valores de los parámetros del modelo de carga con el método de proyección variable.
Origen de datos (C5)
En la fila C5 de la Tabla 1 se observa que, salvo las mediciones de PMU’s y AMI, todas las demás tecnologías de medición han sido utilizadas cada vez menos en el modelamiento de carga. Los sistemas SCADA debido a su baja tasa de reporte (≈ 4 segundos) que no permite capturar la dinámica de las cargas. Los analizadores de calidad de energía debido a que no suelen estar instalados permanentemente. Razones similares aplican para otras tecnologías de medición [29], [61]. Por otro lado, se puede afirmar sin lugar a dudas que la tendencia actual es la utilización de mediciones sincrofasoriales (PMU) en el modelamiento de carga, 53% de PdP en los últimos 5 años. Esto se debe a que su alta tasa de reporte (hasta 50 o 60 veces por segundo) permite capturar el comportamiento estático y dinámico de las cargas.
Lo indicado en el párrafo anterior y observado en la Tabla 1 se confirma en las investigaciones [29], [61]. En [29] se evalúa el rendimiento del método de mínimos cuadrados para estimar modelos ZIP. Esta evaluación se realiza con datos cada 15 minutos (AMI), 5s (SCADA) y 10 ms (uPMU). Una de sus conclusiones es que la precisión del modelo estimado se relaciona fuertemente con la tasa de reporte de los datos; una mayor tasa proporciona mejores resultados. De manera similar, en [61] se evalúa diferentes tasas de reporte de las PMU’s: cada 4s (podría ser SCADA), cada segundo y 30 veces por segundo. La precisión de los modelos de carga obtenidos es: 68%, 79% y 96%, respectivamente.
Un área poco investigada, 5% de PdP, es la utilización de datos de medidores inteligentes de los sistemas AMI para el modelamiento de carga. Lo anterior junto al gran despliegue actual y futuro de AMI lo convierte en un nicho futuro de investigación.
Dos artículos de la Tabla 1, [83], [66], proponen utilizar datos AMI para estimar parámetros de modelos de carga. Los dos se enfocan en el modelo ZIP. En [83] se destaca la dificultad de capturar la dependencia de la carga con la tensión con mediciones AMI cada 15 minutos; como solución propone utilizar técnicas de minería de datos (Kullback-Leibler divergence y K-subspace method) para agrupar cargas/usuarios y posteriormente obtener el modelo ZIP; concluye que aún hay muchas limitaciones. En [66] se propone un método no intrusivo para detectar la actividad de equipos eléctricos dentro de los hogares, asignarles un modelo ZIP y finalmente agregarlos para llevarlos aguas arriba a barras de media tensión; la principal desventaja de esta propuesta es que necesita datos cada segundo; los sistemas AMI suelen reportar datos en el orden de los minutos.
Tipos de mediciones (C6)
En la última década la mayoría de trabajos (PdP de 73%) han utilizado los registros de cuando sucede un evento para modelar la carga. Esto es razonable ya que si no sucediera ninguna variación en las señales (tensión, corriente, potencia, etc.) sería imposible la identificación paramétrica. Cuanto mayor magnitud tiene una perturbación, relativamente menos complejo se vuelve la estimación de los parámetros de los modelos. Dado que los eventos no suceden (y no deberían) frecuentemente en los sistemas, la tendencia actual es investigar el modelamiento de carga con datos tipo ambiente (24% de PdP).
Los trabajos [29], [38], [61] investigan la identificación paramétrica del modelo estático ZIP con datos tipo ambiente de PMU’s. Las técnicas utilizadas son: mínimos cuadrados [29] y algoritmos genéticos [38], aunque en [61] se propone un algoritmo llamado “Adaptive Search” el cual se compara con los métodos de mínimos cuadrados y mínimos cuadrados no lineales. El algoritmo “Adaptive Search” tiene un desempeño sumamente superior, sin embargo, no se ha comparado frente a los algoritmos genéticos.
La estimación del modelo dinámico ERL con registros de eventos ha sido estudiado en [26], [31], [33], [44], [58]. Las técnicas utilizadas son: mínimos cuadrados, mínimos cuadrados no lineales [26], [31], [58], “Levenberg - Marquardt” [33] y, “Unscented Kalman Filter” [44]. La precisión alcanzada es satisfactoria, salvo en [31] que resalta que el método de mínimos cuadrados tiene limitaciones para estimar el modelo ERL de potencia reactiva.
En [39], [40], [56] se investiga la estimación del modelo ZIP+IM con registros de eventos. En [39] se evalúa la técnica de optimización por enjambre de partículas (PSO) y se propone un PSO mejorado (IPSO). Los resultados son satisfactorios con errores de 13% y 1.1%, respectivamente. En [40] igualmente se propone un PSO mejorado (IPSO) y se compara contra otras técnicas: algoritmos genéticos (GA) y mínimos cuadrados no lineales (NLS). Las técnicas IPSO y GA presentan errores inferiores a los NLS. IPSO y GA tienen errores satisfactorios y similares, sin embargo, IPSO tiene mejores características de convergencia y por lo tanto menores tiempos de cálculo. En [56] se propone un análisis de sensibilidad de los parámetros del modelo ZIP+IM, de esta manera se reduce de 12 a 9 parámetros. La optimización se realiza con el algoritmo Levenberg-Marquardt. Se demuestra que la precisión con 12 y 9 parámetros es prácticamente la misma, sin embargo, el tiempo de cómputo se reduce en poco más del 25%.
Pocas publicaciones, [57], [77], se enfocan en los modelos de mayor complejidad como el WECC (tiene 131 parámetros a ser identificados) y CLOD. Estos trabajos se basan en algún tipo de red neuronal o aprendizaje profundo. La principal limitante es la información necesaria para entrenar dichas redes neuronales. Esta información se basa en modelos de carga obtenidos por identificación paramétrica basada en componentes y que está disponible para la red eléctrica de EEUU. Es justamente aquí donde se encuentran los desafíos de utilizar los modelos WECC y CLOD en otras regiones geográficas.
En las técnicas de identificación paramétrica de modelos de carga dinámicos con datos tipo ambiente es donde se encuentran mayores desafíos. La mayoría de trabajos investigan técnicas de optimización metaheurísticas y/o de búsqueda de mínimos globales [51], [69], [79], como: interior-point algorithm (IPA), active set algorithm (ASA), differential evolution algorithm (DEA) y grid search algorithm (GSA).
Es importante mencionar que hasta la actualidad ha resultado imposible identificar algunos parámetros de los modelos de carga sin la ocurrencia de eventos. Lo anterior junto a la poca investigación actual (3% de PdP) en el aprovechamiento conjunto de mediciones de eventos y tipo ambiente hacen que esta área se convierta en un campo futuro de investigación.
Tipo de ejecución (C7)
En la última fila (C7) de la Tabla 1 se observa que hasta el año 2015 el 96% de trabajos proponía/utilizaba metodologías de modelamiento de carga fuera de línea. Su principal desventaja es el gasto de recursos humanos en su ejecución, sin contar la cantidad limitada de modelos de carga que se obtienen.
De igual manera en la Tabla 1 se observa y resalta que la tendencia actual son las metodologías de modelamiento de carga pensadas para ejecutarse de forma automática y en línea. Su PdP ha crecido de 4% a 21% para los periodos 2010-2015 y 2016-2021.
En cuanto a las ventanas de tiempo para el modelamiento de carga en línea o en tiempo real, los trabajos proponen: i) una ventana de 0.3 segundos (30 muestras de uPMU’s) la cual se mueve 50 ms cada vez, es decir, la ventana toma 5 nuevas muestras cada vez que se mueve, más 25 repetidas [29]; ii) extraer una ventana de 10s de cada 15 minutos de datos de PMU’s. Esta ventana es la que contenga la mayor variación o perturbación. [79] indica que 10s son suficientes para modelar la carga y que es computacionalmente eficiente.
Con respecto al preprocesamiento de datos necesario para las metodologías en línea o en tiempo real, los trabajos proponen: i) detectar anomalías de datos de PMU’s con la utilización conjunta de Linear Regression, Chebyshev y, DBSCAN, más una técnica de “unsupervised machine learning” [61]; ii) Prony se utiliza para eliminar pequeñas oscilaciones (ruido) y rápidas variaciones (eventos) de la ventana de tiempo [61]; iii) en cuanto a las técnicas de filtrado [26] propone: robust local regression (RLR), FIR, Savitzky-Golay (SG) y Moving average (MA), recomienda FIR.
El tiempo de ejecución de los algoritmos de modelamiento de carga es fundamental en las metodologías en línea o en tiempo real. Algunas técnicas de optimización propuestas son: mínimos cuadrados [29], mínimos cuadrados no lineales [26], “Adaptive Search” [61] y, “Unscented Kalman Filter” [44]. Mayor investigación hace falta en esta temática sobre todo en cuanto al tiempo de ejecución. Un área poco investigada y nicho futuro de investigación es el modelamiento de carga en tiempo real, tan solo tiene 4% de PdP.
Finalmente, un tema bastante importante en el modelamiento de carga es determinar las barras de carga de un sistema que necesitan ser modeladas y, además, con qué precisión. En este sentido, en [18] se presenta una metodología que permite determinar las barras de carga que deben ser modeladas detalladamente en un sistema y un método probabilístico para determinar la exactitud necesaria en los parámetros de los modelos de carga.
CONCLUSIONES
En este trabajo se realizó una revisión bibliográfica sobre modelamiento de carga con literatura que data a partir del año 2010. El principal aporte de este trabajo fue la determinación de las tendencias actuales y campos futuros de investigación en relación al modelamiento de carga. Para lograr lo anterior se propuso, a conocimiento de los autores, la primera metodología de clasificación bibliográfica enfocada específicamente en el modelamiento de carga.
Las tendencias actuales y áreas poco investigadas se resumen en las dos últimas columnas de la Tabla 1, sin embargo, a continuación, se describen, a criterio de los autores, los principales campos futuros de investigación:
Existe un mayor campo de investigación en la identificación paramétrica antes que en los modelos carga; esto puesto que en la literatura se ha observado una amplia cantidad de modelos de carga y sobre todo acordes para casi todos los tipos de estudios que se realizan a los sistemas eléctricos de potencia.
Dentro de las técnicas de identificación paramétrica se observa que la tendencia es que se ejecuten de forma automática, continua, en línea o hasta en tiempo real. El objetivo es obtener modelos de carga de una gran cantidad de escenarios de operación. Técnicas de aprendizaje de máquina y Big Data se han empezado a utilizar en el modelamiento de carga, sin embargo, hace falta mayor investigación.
Un gran campo de investigación es la identificación paramétrica con enfoque híbrido. Seguramente se contará, en un futuro, con gran cantidad de información proveniente de sensores inalámbricos, HEMS, IoT, entre otros.
Las redes neuronales artificiales (ANN) no son las más utilizadas como modelos de carga, sin embargo, tienen un gran potencial para ser utilizadas como técnicas de identificación paramétrica, es decir, que sus variables de salida sean los parámetros de modelos de carga comúnmente utilizados (ej. ZIP, ZIP+IM, etc.).
Una tendencia actual es el modelamiento de carga con el fin de suplir modelos validados a estudios que evalúan la dinámica RMS de los sistemas, sin embargo, en un futuro, cuando haya gran participación de electrónica de potencia (sea en generación distribuida o en la carga), harán falta modelos de carga para evaluar la estabilidad subciclo. Este es el campo menos investigado que han identificado los autores de este trabajo.