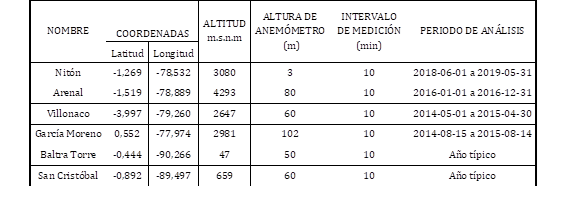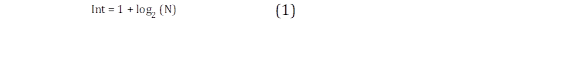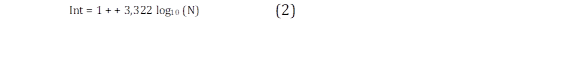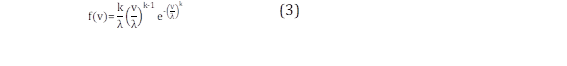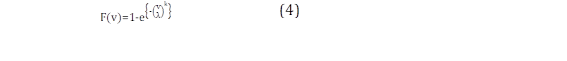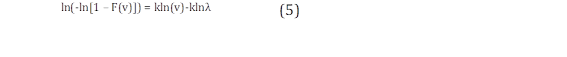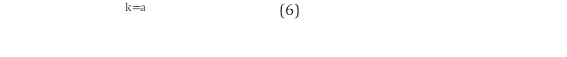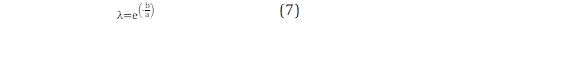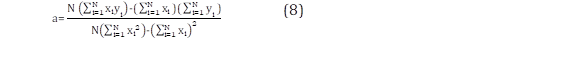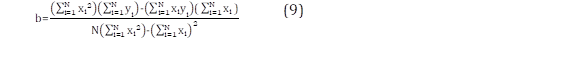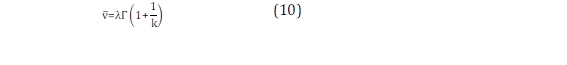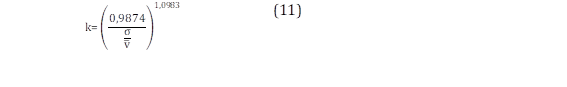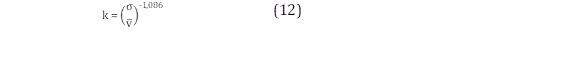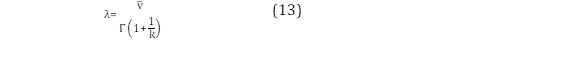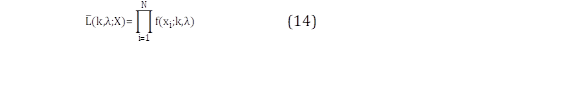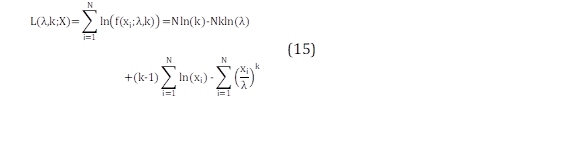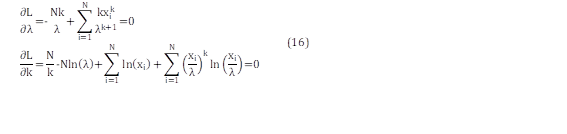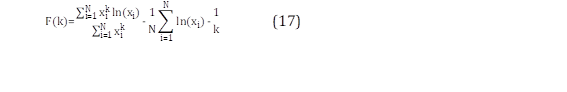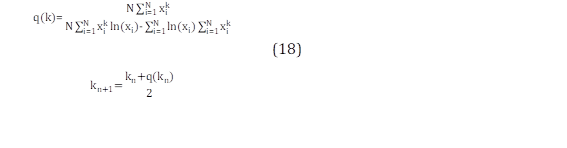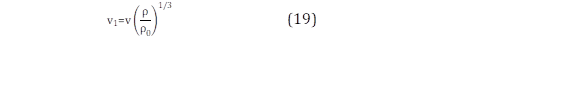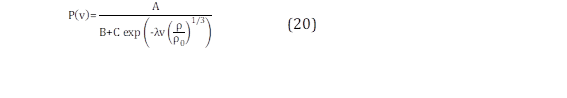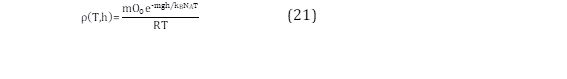INTRODUCCIÓN
El análisis de datos meteorológicos es muy importante para garantizar un estudio apropiado del recurso renovable disponible en una zona. En el caso del recurso eólico, se requiere de un estudio detallado de los datos con información de velocidad y dirección de viento a distintas alturas.
En este sentido, se han desarrollado varias metodologías para procesamiento, control, tratamiento y análisis estadístico de los datos registrados como se muestra en [1]-[5], lo cual permite ampliar el número de sitios seleccionados para la futura instalación de parques eólicos.
Una de estas metodologías se basa en la distribución de Weibull, la cual se utiliza para analizar y caracterizar el comportamiento del recurso eólico según el registro histórico del sitio de interés. Este análisis permite realizar simulaciones para calcular el factor de rendimiento, la proyección de generación o determinar la distribución de turbinas del futuro parque eólico.
De acuerdo con [6]-[9] existen diferentes métodos utilizados para calcular las constantes de la función de distribución de Weibull de 2 parámetros, así como indicadores estadísticos de rendimiento para comparar los modelos. Por otro lado, B. Sürücü and H. S. Sazak [10] proponen la distribución de Weibull de 3 parámetros los cuales utilizan los métodos de máxima verosimilitud, mínimos cuadrados y de momentos para encontrar el parámetro de forma no dimensional, el parámetro de escala y el parámetro de ubicación.
En la actualidad, en Ecuador no se ha realizado un estudio que permita comparar los diferentes métodos de estimación de las variables de la distribución de Weibull para calcular la velocidad media de un emplazamiento y su influencia al estimar el potencial Eolo-eléctrico y el factor de rendimiento. Este estudio es de especial relevancia al tomar en cuenta que el análisis de las series temporales de viento puede determinar la selección de un lugar para instalar un parque eólico, lo cual viene complementado con inversión, incremento de plazas de trabajo y disminución de emisiones de gases de efecto invernadero por la quema de combustibles fósiles para generación de energía.
En este trabajo, se realiza la comparación de 4 métodos de estimación de los parámetros de Weibull para calcular la velocidad media y estimar el factor de rendimiento de un aerogenerador en 7 puntos del país. Los resultados obtenidos muestran que todos los métodos presentan ventajas y limitaciones, sin embargo, el método que presentó menores errores con la función de interpolación fue el MLE.
El documento es organizado de la siguiente manera. En primer lugar, se presentan la metodología utilizada para evaluación de los métodos de estimación de los parámetros de Weibull. Posteriormente se analizan los resultados obtenidos mediante figuras y cuadros estadísticos comparativos de tres métodos de evaluación de rendimiento. Finalmente, se realiza la estimación del Potencial Eolo-eléctrico y el factor de rendimiento de un aerogenerador de 2 MW en 7 sitios del Ecuador y se presentan las conclusiones y recomendaciones del trabajo.
METODOLOGÍA
La metodología de este trabajo se divide en tres etapas:
Estimación de los parámetros de la distribución de Weibull por 4 métodos diferentes para cada base.
Comparación de resultados obtenidos con cada método.
Estimación del Potencial Eolo-eléctrico y el factor de rendimiento.
Serie temporal de datos
Los datos utilizados para el estudio se pueden observar en la Tabla 1; estos corresponden a 4 lugares en Ecuador Continental y 3 sitios en Ecuador Insular.
Las bases de datos elegidas tienen características diferentes en su recurso eólico, lo cual permite evaluar cómo se comporta el ajuste de cada método de la distribución de Weibull dependiendo de la agrupación de los datos de viento en frecuencias relativas obtenidas mediante la ley de sturges como se muestra en (1) y (2) a excepción del método de Máxima Verosimilitud [11]-[13].
Donde N es el número de datos de la serie temporal e Int corresponde al número de intervalos o clases.
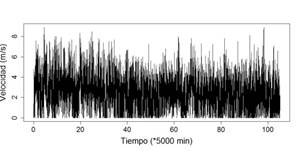
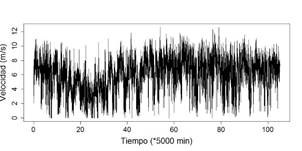
Las Fig. 1 y 2 muestran el comportamiento temporal de las series de Nitón y Baltra.
Estimación de los parámetros de la distribución de Weibull
La función de densidad de probabilidad bajo la distribución de Weibull es ajustada a las frecuencias relativas de la velocidad del viento, como se muestra en (3) [14].
Donde, k y λ corresponden los parámetros de forma y escala y v es la variable de velocidad de viento para la matriz de frecuencias relativas.
La función acumulativa de Weibull se muestra en (4)
Método de linealización (Lin)
El método utiliza la función acumulativa de Weibull mostrada en (4) para estimar los parámetros de forma y de escala que mejor se ajustan a las series temporales [15]. Para ello se realiza la linealización de la función como se observa en (5) [15].
La ecuación resultante es del tipo lineal y se resuelve mediante el método de mínimos cuadrados para hallar las incógnitas k y λ de la función de distribución de Weibull como se indica en (6) y (7).
Donde a y b se despejan de la ecuación lineal y se calculan con (8) y (9)
Método de momentos (Mom)
El método de momentos provee estimaciones acertadas acerca de los momentos poblacionales de serie temporal. Las ecuaciones resultantes para estimar los parámetros k y λ se muestran a continuación en (10) y (11) [16].
Donde v corresponde al valor de la velocidad media y σ a la desviación estándar.
Método Empírico (Emp)
Las ecuaciones para estimar los parámetros k y λ mediante el método empírico se muestran a continuación [8], [9].
Método de estimación por máxima verosimilitud (MLE)
El método de máxima verosimilitud es acreditado al estadístico por R.A Fisher [17], el cual consiste en ajustar el modelo de la función de densidad de probabilidad de Weibull a los datos discretos de velocidad [17], [18], como es observado en (14) [19].
Donde, N es el número total de datos registrados en X como de velocidad del viento, xi son los valores de velocidad de viento correspondientes a la serie de análisis X y f x i ;k, λ corresponde a la función de densidad de probabilidad con distribución de Weibull. Con el fin de resolver el producto de (14), se obtiene el logaritmo natural como es presentado en (15) que es la función de verosimilitud.
La función de verosimilitud expresada en (15), es maximizada al derivar para cada uno de sus parámetros e igualar a cero las funciones resultantes como es mencionado en el trabajo de Balakrishnan et al [20]. Las funciones resultantes obtenidas al aplicar la maximización en (15) para la función de densidad de probabilidad con distribución de Weibull de 2 parámetros es expresada en (16).
Como es posible apreciar en (16), la variable λ puede quedar en función del parámetro k, permitiendo construir una función únicamente dependiente de k que es igual a cero, la misma que es expresada en (17).
Las soluciones para la ecuación mostrada en (16) se lo realizan por diferentes métodos numéricos como Newton Raphson para despejar la variable k [17], [20]-[24]. En este trabajo, se considera la aproximación realizada por Qiao et al [22], donde se propuso un método de convergencia que permite estimar el valor de k. El método de estimación propuesto por Qiao et al [22], es presentado en (18).
El método de máxima verosimilitud estudiado es aplicable a todos los observables x i >0, debido a que el logaritmo natural en el interior de las funciones debe existir para poder estimar el parámetro k. Esta es una limitación del presente método, debido a la naturaleza del registro de velocidad de viento, donde se podrán encontrar valores iguales a cero, o lo que equivale a un viento en calma. Por esta razón, en el presente estudio se propone realizar una restricción con los valores de velocidad de viento mayores a cero, evitando indeterminaciones en los cálculos y garantizando la solución de la función de verosimilitud para cualquier tipo de serie temporal de velocidad de viento.
Comparación métodos.
La comparación de los métodos se ha realizado mediante 3 evaluadores del rendimiento de los estimadores mediante el método de residuos, error cuadrático medio (ECM) y correlación (r) [25], [26].
Potencial Eolo-eléctrico y factor de capacidad
El factor del capacidad se estima con el método del Potencial Eolo-eléctrico propuesto por Jijón et al. [27], donde se determina el potencial eléctrico a partir de la aproximación de la curva de potencia de un aerogenerador de 2 MW, donde se ajusta una función sigmoide. En este trabajo, se considera la corrección de la velocidad por la densidad del aire proveniente de la Ley de Betz, la misma que se puede apreciar en (19).
Donde, v es la velocidad de viento con una densidad del aire ρ, ρ0 es la densidad del aire a nivel del mar y temperatura de 15 ºC, con un valor igual a 1,22 (kg/m3) [28]. El potencial Eolo-eléctrico, basado en una función sigmoide queda expresado en (20).
Donde P(v) es la potencia sigmoidal aproximada y v es la velocidad del viento observada, A, B, C y λ son las constantes de la interpolación no lineal.
La densidad del aire, según el trabajo de Jijón et al. [27], es aproximada a través de las variables de temperatura media y altitud, como se puede apreciar en (21).
Donde, ρ(T, h) es la densidad del aire, Oo es la presión atmosférica a nivel del mar, la cual se aproxima a 1010 (mb), m, g, NA y kg son constantes correspondientes a la masa molar del aire, gravedad, Avogadro y Boltzmann, respectivamente. Por último, R es la constante universal de los gases, T es la temperatura ambiente y h la altitud.
Con esta información base y mediante mapas de temperatura media y modelo digital del terreno, se estiman los valores de potencia media a los que los aerogeneradores estarían funcionando con la velocidad del viento media anual obtenida de la distribución de Weibull [27], [29].
El factor de capacidad corresponde al factor de planta esperado de un aerogenerador en un sitio bajo las condiciones ambientales analizadas en este trabajo; donde su estimación se muestra en (22).
Donde FC es el factor de capacidad, P(v) es la potencia media del aerogenerador y Pn es la potencia nominal igual a 2000 (kW), basado en el aerogenerador modelo del Atlas Eólico 2013 [30].
ANÁLISIS DE RESULTADOS
Evaluación de métodos de estimación
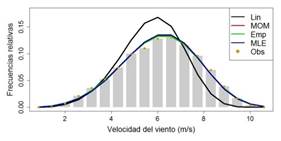
En las Figura 3 a Figura 6 se muestra la interpolación de Weibull bajo los métodos de interpolación descritos en la metodología y su respectivo análisis de residuos.
En la Figura 3, el método de linealización presenta un ajuste más distante que los otros métodos comparados. En este método, la curva se ve desplazada hacia la izquierda y con un pico de frecuencia más alto. La Interpolación con MLE, momentos y método empírico tiene resultados muy similares y valores ajustados cercanos a los valores de frecuencias relativas.
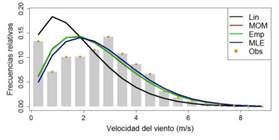
En la Figura 4, se aprecia que los datos se concentran en velocidades bajas cercanas a cero. El método de linealización presenta un ajuste más cercano al primer valor de frecuencia, pero también se observa un desplazamiento a la izquierda por la forma en que la curva desciende anticipadamente. Los métodos de MLE, momentos y empírico tienen un comportamiento similar. Estos tres métodos no son tan sensibles al primer intervalo como en método de linealización, lo cual es una limitación al momento de analizar series de viento con un alto número de registros con velocidades iguales a cero.
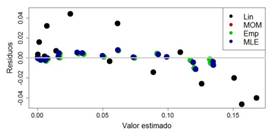
Figura 5: Comparación de residuos métodos de interpolación de parámetros para serie de datos “Baltra típico”
Como se puede observar en la Fig. 5, los valores residuales también serán similares entre los métodos de MLE, momentos y empírico. Sus residuos oscilan entre ±0,015, observándose homocedasticidad en los residuos. En el método de linealización los residuos varían entre ±0,04 y se observa también que también existe homocedasticidad. Los valores más altos de residuos se observan en frecuencias bajas y altas.
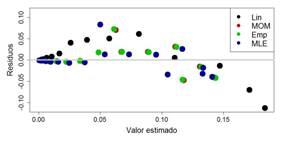
Figura 6: Comparación de residuos de métodos de interpolación de parámetros para serie de datos “Nitón”
En la Fig. 6, el método de linealización muestra heterocedasticidad al observarse que las frecuencias crecen con los residuos. En los métodos de MLE, momentos y empírico, la varianza de los residuos no crece al aumentar la frecuencia.
El comportamiento observado en el ejemplo de la Fig. 4 para la base de Nitón, se pudo apreciar en las series de viento de García Moreno y El Arenal, donde existe un alto número de registros para velocidades cercanas a cero. Además, los MLE, momentos y empírico presentaron las menores diferencias en el análisis de residuos para todas las bases analizadas en este trabajo.
Comparación estadística
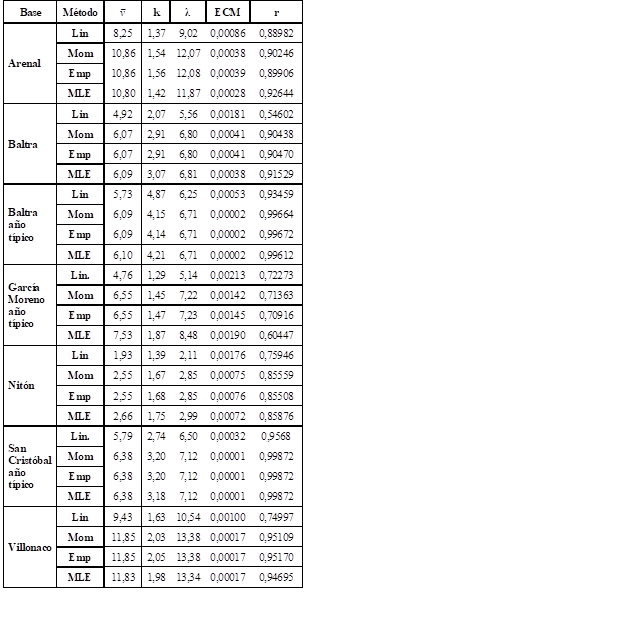
En la Tabla 2 se muestra la comparación estadística de los métodos y bases analizados.
Tabla 2: Tabla de comparación estadística de métodos
Como se pudo observar en la Tabla 2, el método de linealización estima la media más baja, en relación con el resto de los métodos analizados. Las medias estimadas con el método de MLE se diferencian en máximo 5% comparado a los métodos empírico y momentos.
El error cuadrático medio (ECM) para el método de linealización es el más alto, seguido de los métodos de momentos y empírico, siendo el MLE el que obtuvo el menor ECM en las series analizadas. Esta tendencia se pudo apreciar para los valores de correlación, a excepción de las series de Villonaco, Baltra año típico y García Moreno, donde la correlación estimada con el método de MLE es menor o igual a los métodos empírico, y momentos.
Análisis del Potencial Eolo-eléctrico y factor de capacidad
La estimación del Potencial Eolo-eléctrico y el factor de capacidad para cada método utilizado y para cada base de este trabajo, se puede observar en la Tabla 3
Como se puede apreciar en el Tabla 3, el Potencial Eolo-eléctrico y el Factor de capacidad tiene los mimos valores para los métodos empírico y momentos debido a la forma de estimación de la velocidad media. En el caso del método de linealización se obtiene los valores más bajos de potencial, esto se puede deber a que este método presenta mayores limitaciones en la interpolación de las variables de la distribución de Weibull.
Los valores de potencial Eolo-eléctrico y factor de capacidad calculados con el método del MLE, en la mayoría de las bases analizadas, son similares a los resultados obtenidos con los métodos empírico y de momentos. Cabe recalcar que el método de MLE fue el que el que presentó el menor error cuadrático medio comparado al resto de métodos.
CONCLUSIONES Y RECOMENDACIONES
Los métodos de momentos y empírico presentan una limitación en la interpolación de los valores de la distribución al tomar en cuenta la media aritmética o matemática para el inicio de los cálculos. Sin embargo, los errores son más bajos que los obtenidos con el método de linealización.
El método de MLE presenta limitaciones de convergencia para encontrar una solución en series de datos con valores de viento de velocidad iguales a 0, debido a que se producen indeterminaciones en el interior de los logaritmos del método.
El método que presentó menor error cuadrático medio (ECM) con la función de interpolación fue el MLE, donde los valores obtenidos para las bases de Arenal, Baltra, Baltra año típico, Nitón, San Cristóbal año típico y Villonaco, son: 0,00028, 0,00038, 0,00002, 0,00072, 0,00001 y 0,00017, respectivamente. El único caso que presentó un valor mayor ECM fue para la base de García Moreno año típico con un valor 0,00190, el cual fue mayor al método empírico y de momentos, donde su valor de ECM para estos métodos fue de 0,00145 y 0,00142.
El método MLE es el que mejor se ajusta para aplicaciones de energía eólica, donde se busca que las series de viento tengan valores de velocidad altos. Para series que registren valores de velocidad de viento bajas, se recomienda analizar el método de linealización, el cual considera los primeros intervalos de la serie.
Se recomienda realizar un análisis de las series de datos de viento que registran valores cercanos a cero, donde se deberá considerar el límite de detección de los sensores utilizados.
Este trabajo demostró la sensibilidad de la metodología del Potencial Eolo-eléctrico, el cual es susceptible a mínimas variaciones en los valores de velocidad media. Esto se pudo apreciar en los resultados expresados en la Tabla 3, donde se recomienda utilizar el método de MLE para esta aplicación.
Los análisis realizados en este estudio muestran la importancia de realizar un análisis exhaustivo a las series de viento, las cuales pueden comportarse de forma variable según el método de interpolación utilizado para obtener la estadística de los datos de viento.
Se recomienda no reemplazar ninguna de las fases de factibilidad de un proyecto eólico con la presente metodología. Sin embargo, estos análisis pueden ser utilizados para brindar información básica de un emplazamiento eólico, o ser incluidos como insumos en las fases de factibilidad de un proyecto, considerando un análisis exhaustivo de las turbinas que pueden adaptarse a un sitio de interés.