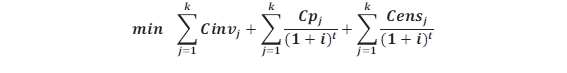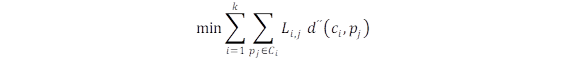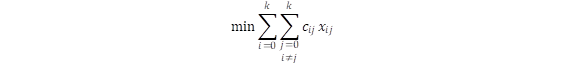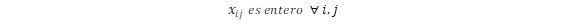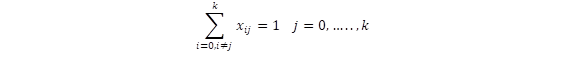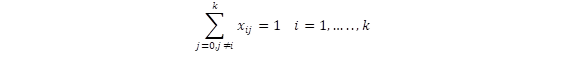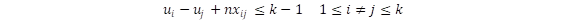INTRODUCCIÓN

La tecnología de los elementos y equipos que conforman el sistema de distribución eléctrica subterránea (SEDS) ha tenido un importante desarrollo en los últimos 20 años. Estos avances han impactado en la seguridad del personal operativo y en la confiabilidad del sistema de distribución. La reducción de los costos asociados a un proyecto de SEDS, con el fin de adaptarlos a la realidad económica de las empresas de distribución del país, es un objetivo que implica el desarrollo de nuevos criterios de planificación, en los que se debe considerar el adecuado aprovechamiento de los avances tecnológicos, permitiendo a su vez mejorar la calidad del producto, la reducción de las pérdidas de energía, y la simplificación de las labores de operación y mantenimiento del SEDS.

Las redes eléctricas subterráneas, por su naturaleza, en general presentan una mayor confiabilidad que las redes aéreas; sin embargo, si el diseño no contempla la incorporación de un equipamiento adaptado al ambiente en el cual va a ser utilizado, esta característica puede verse desmejorada y convertirse en un serio inconveniente en la etapa de operación, con graves afectaciones en la continuidad del servicio eléctrico [1]. Es muy importante puntualizar que, la selección de la configuración topológica de los alimentadores primarios durante la etapa de planificación de un proyecto de SEDS, incide directamente, no solamente en los costos de inversión, operación y mantenimiento sino también en los de confiabilidad. En consecuencia, a lo descrito, la topología del sistema primario debe ser elegida, presentando como objetivos: un alto nivel de confiabilidad, una reducción en el grado de complejidad de la operación, costos adecuados a la realidad nacional y lo intuitivo del sistema de protecciones.

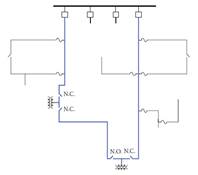
Una configuración primaria de redes de distribución subterránea que cumple con los objetivos señalados es la de tipo “Open Loop” (OL - anillo abierto). Como se aprecia en la Fig. 1, esta configuración tiene la ventaja de una doble alimentación primaria que permite restituir una parte importante de la malla en caso de averías, lo que, a diferencia de la red radial, reduce notoriamente el tiempo de interrupción que experimentan los usuarios [2].

Figura 1: Configuración Open Loop. 

El empleo de este esquema de alimentación primaria plantea varias interrogantes, que deben ser absueltas durante la etapa de planificación, a saber: ¿cuántos anillos OL se deben formar?, ¿cuántos equipos de maniobra y protección se requieren?, ¿cuál es el mejor recorrido de los circuitos primarios?, todo esto en el contexto de brindar un servicio de alta confiabilidad y a los menores costos de inversión y operación posibles.

Para dar respuesta a estas inquietudes se configuran varios problemas de optimización que, por su formulación matemática, son del tipo no lineal entero mixto (PNLEM). Estos problemas se pueden abordar mediante técnicas de Programación Dinámica, dividiendo en partes el problema total y resolviendo cada una de ellas mediante la aplicación de algoritmos heurísticos.

Entre las principales características de los SEDS se puede resaltar que normalmente estos se construyen en sectores urbanos altamente consolidados, y que por lo tanto presentan un bajo crecimiento de demanda eléctrica. Se debe considerar adicionalmente para su implementación, se realiza el reemplazo integral de toda la infraestructura de servicio existente. Estos aspectos descritos determinan que el desarrollo de la planificación de SED empleado sea del tipo Greenfield, en la cual se requiere como datos de entrada a la carga eléctrica del usuario final y su distribución geográfica en el área de estudio [3].

METODOLOGÍA DE PLANIFICACIÓN PROPUESTA

Para el desarrollo de una metodología de planificación de SEDS que permita encontrar la configuración óptima de los circuitos primarios considerando la configuración topológica OL, se aborda la resolución del problema mediante el empleo de la técnica de Programación Dinámica (PD), es decir dividiendo el problema de optimización en subproblemas cuya resolución secuencial produce una solución integral [4]. A continuación, se presentan los subproblemas considerados en la metodología propuesta y los algoritmos heurísticos empleados en la solución respectiva.

Determinación del número de equipos de maniobra y/o protección (EM&P).

Se plantea un problema de optimización de costos cuya función objetivo es:

Sujeto a la siguiente restricción:

Dónde:

Debido a que se configura un problema de optimización del tipo No lineal Entero Mixto, para su resolución se emplea el Algoritmo Genético (AG). Este algoritmo ha sido desarrollado para resolver problemas lineales y no lineales, explorando las regiones del espacio de búsqueda a través de la mutación, cruzamiento y la selección de operaciones aplicadas a los individuos en una población.

En el proceso del desarrollo del algoritmo, las poblaciones con mejores soluciones evolucionan hasta que se satisface un criterio de terminación [5].

Sectorización espacial de los circuitos primarios

Dado un grupo de cargas eléctricas L 𝒊,𝒋 (CT MV/BV) con su ubicación geográfica determinada mediante un sistema de coordenadas cartesiano 𝒑 𝒋 =( 𝒙 𝒋 , 𝒚 𝒋 ), se plantea el siguiente problema de minimización [6]:

Función Objetivo:

Dónde:

Para la solución de este problema se emplea el algoritmo K-Medoids, el cual es un método de agrupamiento (clustering), que se deriva del algoritmo K-Means que fue propuesto por Kaufman, L., and Rousseeuw, P. J en 1987 y actualizado en 1990 como algoritmo PAM (Partitioning Around Medoids) [7]. Este método basa su agrupamiento en función de encontrar el costo mínimo entre una observación (coordenadas) con cada uno los medoides previamente determinados.

Determinación de la ruta óptima de los circuitos primarios en configuración OL en cada sector

La formulación de este problema mediante el modelo matemático de programación lineal entera mixta se presenta en [5] y se detalla a continuación:

Función Objetivo:

Sujeto a las siguientes restricciones:

Dónde:

Para la resolución de este problema se emplea el algoritmo de optimización de colonia de hormigas (Ant Colony Optimization - ACO). Este algoritmo está basado en el comportamiento de las hormigas cuando buscan su alimento y retornan a su colonia luego de que lo han encontrado. Las hormigas exploran por diferentes caminos aleatorios, el momento que alguna encuentra una fuente de alimento, regresa a su colonia dejando un rastro de feromonas que se disipa con el tiempo, este rastro es percibido por otras hormigas las cuales siguen por ese camino. Si es que alguna otra hormiga ha encontrado una ruta más corta regresará en un menor tiempo por esta nueva vía, permitiendo que las feromonas se disipen más lentamente, esto indica a las otras hormigas que este nuevo camino es el más óptimo, haciendo que ellas prefieran recorrer esta nueva ruta. Al haber una mayor cantidad de hormigas por la nueva ruta, se refuerza el rastro de feromonas llegando a un punto en que todas las hormigas preferirán recorrer únicamente este camino.

Este algoritmo fue desarrollado por Marco Dorigo en 1997 como una mejora del algoritmo de Sistema de Hormiga presentado en 1996 por el mismo Dorigo [8].

La aplicación de este algoritmo de optimización se realiza especialmente en problemas de grafos, en ellos cada hormiga artificial tiene la misión de construir una solución del problema, cada adición a la solución parcial construida, se realiza a través de una regla de decisión estocástica, que incluye información heurística e información del resto de las hormigas. Luego de la construcción o durante el proceso, las hormigas evalúan la solución y depositan feromona en las conexiones utilizadas, que servirá de información para el resto de las hormigas artificiales.

Además, se realiza la evaporación, es decir la eliminación de feromona en cada iteración del problema, de manera de favorecer la exploración en nuevas zonas de búsqueda.

DESARROLLO COMPUTACIONAL

Para la implementación de la metodología descrita se desarrolló un programa en lenguaje M de MATLAB, que utiliza como datos de entrada: la información de la ubicación geográfica junto con la potencia de los CT MV/BV, y el grafo con las coordenadas georreferenciadas de las vías y calles que conforman el área de estudio. La fuente de esta información proviene de la base de datos GIS, sistema de información geográfica de redes de distribución, de las empresas eléctricas, y de un análisis previo realizado para determinar la ubicación óptima de los CT MV/BV.

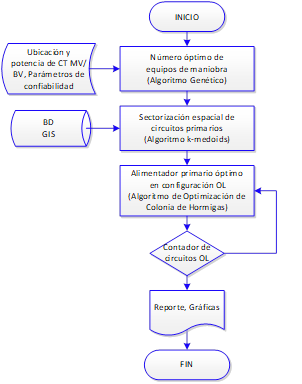
El diagrama de flujo, que describe el proceso metodológico y su implementación computacional, se presenta en la Fig. 2.

Figura 2: Diagrama de flujo de la metodología de planificación desarrollada 

EJEMPLO DE APLICACIÓN METODOLÓGICA

Como aplicación práctica de la metodología desarrollada se realizó el análisis en un sector urbano de la ciudad de Ambato con una superficie de 2.97 km², que cuenta con 11.276 clientes y un consumo promedio mensual de 113 kWh/usuario. Esta información, conjuntamente con el grafo de las vías y calles de la zona de estudio, fueron obtenidas de la base de datos (BD) del sistema GIS de la Empresa Eléctrica Ambato S.A. (EEASA).

El tiempo de procesamiento computacional que tomó este ejemplo fue de 81,22s (1min, 21s) empleando una PC con las siguientes características: procesador INTEL Core i7 8th Gen 1.99Ghz 64 bits, 8 Gbytes de RAM.

Datos de entrada

En las Tablas 1 y 2 se muestran los parámetros financieros de entrada para la función objetivo; y, los parámetros de confiabilidad se muestran en la Tabla 3 [10]. La tasa de crecimiento de la carga se determinó de un estudio previo de pronóstico de la demanda.

Tabla 1. Parámetros financieros de entrada 

Tabla 2. Otros parámetros de entrada 

Tasa de descuento (%)	Tiempo de vida útil (años)	Tasa de crecimiento de la carga (%)	Potencia máxima por OL (MW)
3,00	25,00	1,50	1,50

Tabla 3. Parámetros de entrada de confiabilidad [10] 

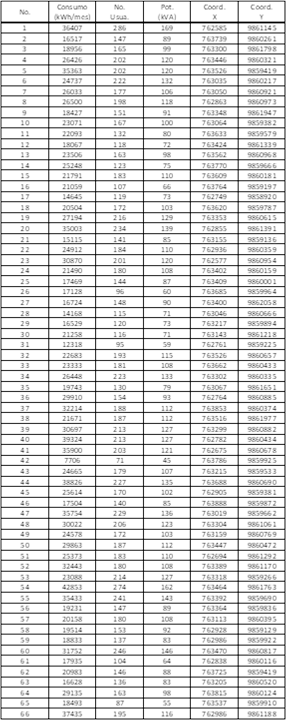
La ubicación georreferenciada y la potencia de los CT MV/BV proyectados en el área de estudio, se obtuvieron mediante la aplicación de una herramienta informática desarrollada para el efecto [11], que a su vez requiere como entrada las coordenadas geográficas y el consumo mensual de los medidores de energía de cada abonado, información recabada de la base de datos GIS de la EEASA. En la Tabla 4 se presentan los datos de los centros de transformación en el área bajo análisis.

Tabla 4. Ubicación geográfica y potencia de los CT MV/BV 

Resultados

Los resultados que entrega la aplicación computacional desarrollada se presentan tanto de forma numérica como gráfica. En la Tabla 5 se muestra el cuadro general de resultados obtenidos mediante la aplicación del AG en la determinación del número de equipos de maniobra y/o protección (EM&P).

Tabla 5. Resultados obtenidos mediante la aplicación de AG 

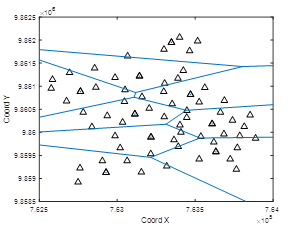
Para la sectorización espacial de los anillos primarios, realizada mediante el algoritmo de clustering K-Medoids, se necesitó de 4 iteraciones para obtener el agrupamiento óptimo para los 9 circuitos OL determinados en la etapa previa. En la Fig. 4 se presentan los correspondientes diagramas de Voronoi.

Figura 4: Diagrama de Voronoi de agrupamiento de CT MV/BV 

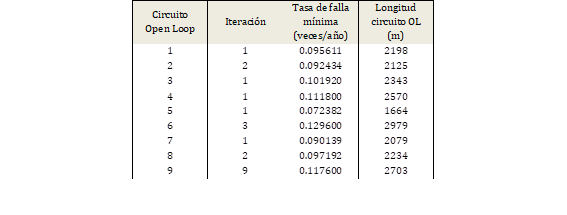
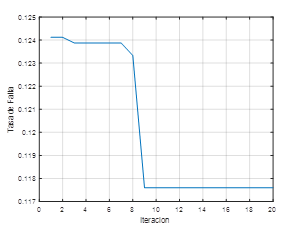
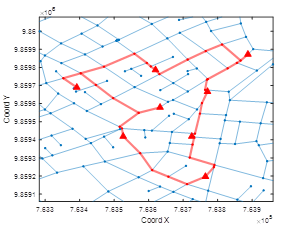
En la Tabla 6 se presentan los resultados obtenidos por cada circuito OL generado y el número de iteraciones necesarios que el algoritmo ACO requirió para minimizar la tasa de falla. En las Figuras 5 y 6 se presentan el número de iteraciones que se requirió para la optimización de la tasa de falla del circuito OL No. 9 y su implantación en el grafo georreferenciado de las calles, respectivamente.

Tabla 6. Resultados obtenidos por circuito OL 

En total se requirió 21 iteraciones con el algoritmo ACO para la determinación del recorrido óptimo de la totalidad de los anillos primarios.

Figura 5: Iteraciones requeridas para optimizar la Tasa de Falla en circuito Open Loop No. 9 

Figura 6: Implantación en grafo de calles del circuito Open Loop No. 9 

Finalmente, en la Fig. 7 se muestra el recorrido de todos los primarios en configuración OL, lo que constituye una propuesta de planificación para la implementación de un sistema eléctrico de distribución subterráneo en una importante superficie urbana.

CONCLUSIONES Y RECOMENDACIONES

En el presente trabajo se desarrolla una metodología que permite realizar la planificación tipo Greenfield de redes de distribución subterránea en amplias zonas urbanas consolidadas. La aplicación de la metodología requiere como datos de entrada las coordenadas geográficas y la potencia de los CT MV/BV y el grafo georreferenciado de las calles y avenidas del área de estudio. Esta información se encuentra disponible en las bases de datos de los sistemas de información georreferenciados (GIS) de las empresas de distribución del país.

La metodología planteada y su desarrollo computacional, permiten generar una propuesta de planificación óptima de un sistema eléctrico de distribución subterráneo en una amplia superficie urbana, considerando criterios muy importantes como la disminución de costos de inversión, la minimización de las pérdidas técnicas de energía y la maximización de la confiabilidad del sistema.

Figura 7:  Propuesta de planificación de circuitos primarios en configuración OL 

Si bien, el empleo de algoritmos heurísticos y de teoría de grafos permiten obtener soluciones óptimas locales, a través del enfoque de programación dinámica se consiguió desarrollar una aplicación computacional que logra obtener, en un tiempo muy reducido, una alternativa de planificación de un sistema de distribución subterránea aplicable a áreas extensas, ahorrando ingentes recursos económicos y humanos en las etapas de planificación y diseño de un proyecto de soterramiento eléctrico.

La determinación del número de equipos de maniobra y/o protección, que la propuesta metodológica entrega como parte de sus resultados, permite reducir sustancialmente el costo total de inversión en la implementación de una red subterránea. Esto se debe a que optimiza la cantidad de estos elementos, los cuales tienen un costo elevado, que representa un porcentaje significativo dentro del valor total del proyecto de soterramiento.

Con una planificación de la topología y las protecciones eléctricas de la red, además del empleo de equipos y materiales adecuados para el medio ambiente bajo el cual opera una red eléctrica subterránea de distribución, se mejora notablemente la calidad del servicio técnico (confiabilidad) y se reduce las pérdidas técnicas de energía; consiguiendo así, volver atractivo el desarrollo de proyectos de soterramiento eléctrico en nuestro medio.