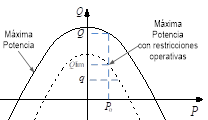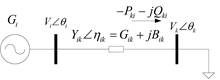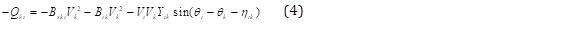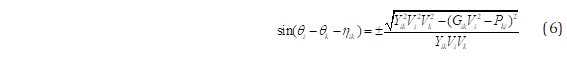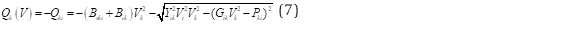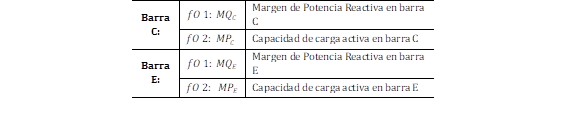Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
Los sistemas eléctricos de potencia se caracterizan por operar cerca de sus límites operacionales, bajo condiciones de alto estrés, cubriendo una demanda que incrementa cada año con una infraestructura cada vez más ajustada.
Desde hace varios años, la asignación de recurso de potencia reactiva en los sistemas eléctricos, para mantener la estabilidad de voltaje, tiene un papel relevante dentro de las perturbaciones que ponen en riesgo la seguridad del SEP [1]-[4]. En este contexto, diversos trabajos han mostrado las ventajas de disponer herramientas o metodologías que determinen márgenes de potencia o cargabilidad del sistema y que permitan gestionar dichos recursos evitando llevar al sistema al colapso de voltaje [5]-[7]. La potencia activa (P), potencia reactiva (Q), voltaje de las barras, están relacionadas en el comportamiento del sistema y en los márgenes de potencia en las barras. En ese marco, los investigadores a lo largo de los años han relacionado estas variables en la curva nariz PV, curva QV y la proyección en la curva PQ para evaluar la estabilidad del sistema o la cercanía al punto del colapso.
Una revisión del estado del arte en relación con los márgenes de potencia activa y reactiva, muestran varias metodologías y softwares para crear las curvas PV, curvas QV, pero existen escasos trabajos relacionados a la curva PQ, para evaluar la cargabilidad en barras del SEP. Algunos autores usan técnicas de modelamiento con problemas multi-objetivo para crear la frontera de Pareto para representar la potencia reactiva versus el voltaje o las pérdidas del sistema[8]. Así por ejemplo, en [9] los autores proponen tres funciones objetivo: recurso de potencia reactiva, pérdidas del sistema y potencia activa; y por medio de un optimizador a dos niveles, usando el algoritmo: Non-dominated Sorting Genetic Algorithm (NSGA-II) y el algoritmo de punto interior, obtienen la frontera de Pareto y se planifica el recurso de potencia reactiva.
Los autores en [10] realizan una optimización multi-objetivo para abordar la compensación de potencia reactiva al sistema eléctrico Paraguayo, considerando restricciones operativas. El método optimiza independientemente varias características relacionadas con la operación de los sistemas de energía: cantidad de equipos compensadores de energía reactiva, pérdidas de transmisión, desviación de voltaje promedio, desviación de voltaje máximo y seguridad de voltaje medida por un índice de margen de carga. Sin embargo, no se grafica la frontera de Pareto en relación con los márgenes de potencia.
En [11] utilizan un problema multi-objetivo para planificar la potencia reactiva, basado en el dominio de Pareto, y usando Particle Swarm Optimization (PSO) para establecer un problema multi-objetivo, en el cual minimizan pérdidas de potencia activa (MW) y el costo total de ubicación de recurso de potencia reactiva.
Los artículos [12]-[18] obtienen la frontera de Pareto de un problema multi-objetivo, minimizando pérdidas de potencia, y la desviación en el perfil de voltaje, aplicando algoritmos como (NSGA-II), Normal Boundary Intersection (NBI), Strength Pareto Multi-group Search Optimizer (SPMGSO), PSO, Tabu Search y herramientas computacionales como GAMS (General Algebraic Modeling System), Matlab, CPLEX, entre otros.
En [19] la frontera de Pareto es formada con funciones objetivo que minimizan pérdidas de potencia activa (MW) y potencia reactiva (MVARs).
En [20] proponen un problema multi-objetivo que dispone como funciones objetivo maximizar la generación de potencia activa, y minimizan el consumo de potencia reactiva en un despacho centralizado en una red de distribución con sistemas fotovoltaicos.
Los trabajos descritos han estimulado a que, en los últimos años, el OPF podría cambiar de un problema de optimización de un solo objetivo a múltiples objetivos; y como resultado se podría obtener varios indicadores para el operador del SEP o herramientas de planificación para la toma de decisiones. Sin embargo, en los trabajos revisados en el no existe problemas multi-objetivo que relacionen la potencia activa y reactiva en la frontera de Pareto.
Por otra parte, la evaluación de estabilidad de voltaje, usando la curva PV, en la punta de la curva de la nariz (punto del colapso) pueden llevar a determinar márgenes de potencia elevados, ya este es el punto de máxima transferencia de potencia y los niveles de voltaje llegan a valores muy inferiores a los límites operacionales reales de los sistemas de potencia [21]. Adicional, las curvas PV y QV analizan los márgenes de potencia considerando únicamente la capacidad de la red, sin considerar las reservas y límites del recurso de generadores. En tal sentido, es necesario evaluar los márgenes de potencia activa y reactiva en las barras del sistema considerando restricciones operativas y límites operacionales reales de los SEP, obteniendo márgenes más conservadores.
El presente trabajo propone una metodología basada en un problema de optimización multi-objetivo para condiciones normales de operación, considerando como objetivo 1: el margen de potencia reactiva, y como objetivo 2: la capacidad de potencia activa en la barra de carga, con el fin de graficar la frontera de Pareto, que representa la curva PQ. La metodología considera los límites reales de operación del sistema incluyendo reservas de potencia reactiva, restricciones de flujos de potencia, límites de las unidades generadoras y límites superiores e inferiores de voltaje en barras. El problema multi-objetivo propuesto usa el algoritmo Multiobjective Genetic Algorithm Solver, del software MATLAB.
En la Sección II se analiza el uso del margen de potencia activa y reactiva en los sistemas eléctricos de potencia. En la Sección III se presenta la metodología propuesta para la obtención de la frontera de Pareto. La Sección IV muestra el desempeño de la metodología propuesta en base a un sistema eléctrico de 5 barras. Finalmente, las conclusiones son presentadas en la Sección V.
MARGEN DE POTENCIA ACTIVA Y REACTIVA EN LOS SEP
El margen de potencia reactiva refleja el stress del sistema establecido por las transferencias de potencia activa [5][22] [23]; por tal razón, es necesario relacionar estas variables en el problema de optimización.
Relación entre voltaje y potencia activa
El margen de potencia reactiva se define como la diferencia entre la carga máxima reactiva que puede ser consumida en una zona determinada (respetando los límites de operación normal), y la carga correspondiente al punto de operación. La Fig. 1 muestra en línea punteada la potencia máxima de una barra de carga considerando las restricciones operativas del sistema, mientras que la línea continua representa el límite teórico sin considerar dichas restricciones.
La ecuación (1) corresponde a la parábola en el Plano PQ, mostrada en la Figura 1 [23].
En donde, “E” es el voltaje de la fuente, “X” es la reactancia de la línea, y “V” es el voltaje en la carga, considerando la Fig. 2.
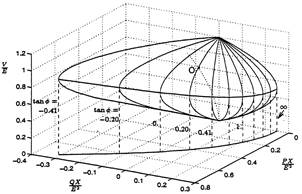
En la Fig. 3 se muestra una gráfica en 3 dimensiones que representa el voltaje en función de la carga activa (P) y carga reactiva (Q) en la barra del sistema eléctrico, considerando diferentes factores de potencia y diferentes puntos de operación. En el plano PX 𝐸 2 , 𝑄𝑋 𝐸 2 se proyecta la curva PQ (proyección de la curva PV y QV sobre el plano PQ) que indica la capacidad de carga [23]. La curva de la Fig. 3 se representa con la ecuación (2) [23]:
Para plantear el modelo propuesto, se requiere relacionar la potencia reactiva y activa en una sola ecuación para ser considerado en el modelo de optimización propuesto.
Relación entre potencia activa y reactiva en una única ecuación
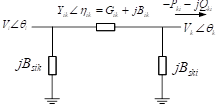
Para relacionar la potencia activa y reactiva en una única expresión matemática, que contemple todos los parámetros y variables de las ecuaciones de flujo de potencia que intervienen en el fenómeno de colapso de tensión, se usa la formulación del artículo [24] y aplicada en [21] en un problema de optimización de una sola función objetivo. Considérese el sistema de la Fig. 4, y su equivalente π mostrado en Fig. 5.
Mediante las ecuaciones de flujo de potencia se define la potencia activa inyectada a la barra “k” (3) y potencia reactiva transmitida (4).
A partir de la identidad:
y usando las ecuaciones (3) y (4) se obtiene:
Al sustituir (6) en (4), se obtiene la potencia reactiva en la barra “k” en función de la potencia activa inyectada en dicha barra “k”, 𝑃 𝑘𝑖 y el voltaje en la misma barra [24]:
PROBLEMA DE OPTIMIZACIÓN MULTI-OBJETIVO
Estructura del Problema de Optimización Multi-objetivo
El problema de optimización multi-objetivo se establece con la Función Objetivo 1: Margen de potencia reactiva ( 𝑀𝑄 𝑘 ) de la carga conectada a la barra "𝑘", definida por la ecuación (8); y la Función Objetivo 2: capacidad de potencia activa (𝑀 𝑃 𝑘 ) de la carga conectada a la barra "𝑘", definida por la ecuación (9); que al maximizar estas dos variables representa el margen de cargabilidad de potencia en diferentes puntos de operación. El proceso de optimización multi-objetivo en cada barra de carga se realiza secuencialmente de forma independiente.
Función Multi-objetivo:
Sujeto a:
La ecuación (10) establece las restricciones de igualdad considerando el balance de potencia reactiva en la barra, considerando en cada ramal el flujo la potencia activa dentro de Q k 𝑉 . Adicional, en dicho balance se considera la carga activa ( 𝑞 𝑘 ) y el margen de potencia reactiva ( 𝑀𝑄 𝑘 ) en la barra. Las restricciones de igualdad definidas en la ecuación (11) expresan el balance de reactivos que debe cumplirse en barras intermedias, sin carga, utilizando la ecuación (7) para los flujos entrantes y salientes (en barras con más ramales, se tendrá: Q k V =− 𝑖=1 𝑛 𝑘 𝑄 𝑘𝑖 donde 𝑛 𝑘 representa el número de elementos). La ecuación (12) establece la restricción de igualdad de flujo de potencia activa en las barras. Los límites de potencia reactiva de los generadores están definidos en la ecuación (13), donde “g” es el número de generador. La ecuación (14) establece los límites de voltajes (V) en barras del sistema eléctrico.
Procedimiento para el cálculo
El procedimiento de resolución se presenta en la Tabla 1, en la cual se utiliza Digsilent Power Factory, Optimizador KNITRO de Artelys [25] y MATLAB. Se utiliza el software Digsilent para validar el modelo eléctrico del sistema mediante un flujo de potencia. Se usa KNITRO con MATLAB para desarrollar el OPF con una sola función objetivo y obtener soluciones factibles para posterior validación del problema multiobjetivo. Para la resolusión del problema de optimización multiobjetivo propuesto se usa el algoritmo Multiobjective Genetic Algorithm Solver, de MATLAB.
SISTEMA DE PRUEBA
Datos del Sistema Eléctrico
Para probar el modelo de optimización multiobjetivo, se modela el sistema de cinco barras que es utilizado en [21], del cual, se muestra los datos y detalles del sistema eléctrico en la Fig. 6. El sistema dispone de 2 barras de carga, 2 barras con control de tensión (barras PV) y una barra intermedia. Las restricciones del problema de optimización se detallan en la Tabla 2.
Las funciones objetivo del problema de optimización se plantea en cada una de las barras de carga (barra C y barra E), definidas en la Tabla 3.
El proceso de optimización multi-objetivo en la barra C y E se realiza de forma independiente.
Resultados
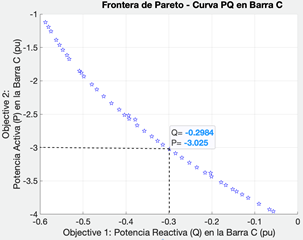
La curva PQ de la Fig. 7 representa la capacidad de carga en la barra C, tanto en potencia activa como en potencia reactiva en “pu”.
En la Fig. 8 se muestra la curva PQ que representa la capacidad de carga en la barra E, tanto en potencia activa como en potencia reactiva en “pu”.
Observación: Los valores obtenidos en los ejes de la frontera de Pareto disponen signos opuestos a los valores de las variables, debido a que el algoritmo requiere anteponer el signo negativo para maximizar las variables de la función objetivo.
Para validar el modelo, se verifica que los márgenes de potencia reactiva en la barra C y barra E obtenidos mediante OPF en el mismo sistema de 5 barras, en [21], se encuentren dentro de la región o espacio de la frontera de Pareto en un punto de operación. Los márgenes de potencia obtenidos para un punto de operación en el OPF con el optimizador KNITRO de Artelys se muestran en la Tabla 4:
Se verifica estos valores de la Tabla 4 en la frotera de Pareto de la Fig. 7 y Fig. 8, y se puede validar que dichos puntos de operación (líneas entrecortadas de las Fig. 7 y Fig. 8), pertenecen a las soluciones factibles de la frontera de Pareto.
Los márgenes definidos por la frontera de Pareto son capaces de identificar la cargabilidad en cada barra considerando las restricciones operativas del SEP.
CONCLUSIONES Y RECOMENDACIONES
En este trabajo se presenta una metodología basada en un problema de optimización multi-objetivo para generar la frontera de Pareto que representa la curva PQ de la barra sujeta a análisis del SEP. La metodología propuesta considera límites operacionales tales como reserva de potencia activa y reactiva del sistema, capacidad de los generadores, así como límites inferiores y superiores de los niveles de voltaje.
Las fronteras de Pareto de cada barra representan los márgenes operativos tanto en potencia activa como en potencia reactiva, el cual puede ser usado como una herramienta complementaria de análisis a las curvas PV y curvas QV, cuando se considere límites y restricciones del sistema en dichas curvas. Los resultados del modelo de optimización multi-objetivo indican que la metodología propuesta cumple con el objetivo planteado, permitiendo identificar la capacidad de carga activa y reactiva con base a los límites del sistema. Se concluye, que con la metodología propuesta se posee una herramienta que le permite a los analistas de los SEP gestionar recursos de potencia reactiva con base a la potencia activa.
AGRADECIMIENTOS
Se agradece a la Campus Beauchef - Universidad de Chile, por los conocimientos impartidos durante los estudios de Magister en Ciencias de la Ingeniería, mención Eléctrica (2010-2012), y a la Universidad Tecnológica Centroamericana (UNITEC) de San Pedro Sula - Honduras por la apertura a las cátedras y al desarrollo a la investigación.
