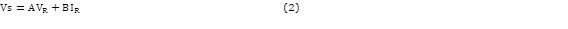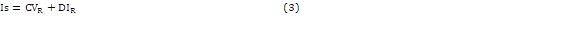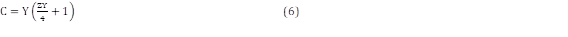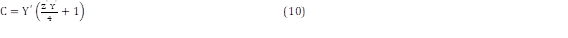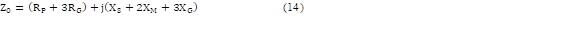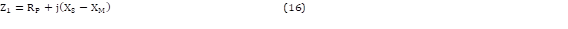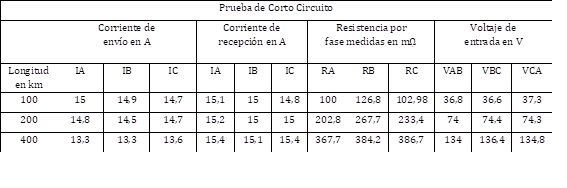INTRODUCCIÓN
En la solución de los problemas asociados a los estudios con líneas de transmisión se asume que los parámetros de la línea se conocen. La determinación más acertada de sus parámetros depende del objetivo del análisis que se realizará en el sistema eléctrico de potencia, el modelo de una línea de transmisión no será el mismo para un estudio del sistema en estado estable que para un estudio de coordinación de aislamiento y el conocimiento de las condiciones transitorias y posibles sobrevoltajes en la línea [1], [2], [3].
Los parámetros eléctricos de una línea de transmisión pueden ser calculados a partir de su geometría y sus componentes, pero la determinación de este modelo basado en los métodos de las funciones de Bessel y Carson producen ciertas imprecisiones debido a las aproximaciones que se utilizan para las condiciones ambientales variantes, la conductividad no homogénea del suelo y la geometría de la torre [2], [4].
Los parámetros de la línea pueden estimarse a partir de mediciones de voltaje y corriente en sus terminales. Quizá uno de los limitantes en la práctica es el instrumento que permita obtener esta medición, se puede utilizar unidades de medición fasorial PMUs o registros de fallas obtenidos de los relés de protecciones de la línea [1], [5]. Si bien es cierto existen diversos métodos para la estimación de parámetros, se debe tener en cuenta que la efectividad de los mismos difiere dependiendo de las características del sistema eléctrico, la geometría de la línea y la dinámica del sistema, de todas formas, cada método de estimación es efectivo para un punto de operación específico del sistema eléctrico y típicamente son pocos los parámetros de las matrices de admitancia e impedancia que se pueden estimar con precisión [6], [7].
Cuando el modelo de la línea se va a utilizar para realizar estudios eléctricos en estado transitorio, se ha reconocido ampliamente que los modelos clásicos de parámetros concentrados constantes no producen resultados satisfactorios pues tienen una independencia de la frecuencia que en el estado transitorio puede tomar un rango amplio de valores. Para afrontar este aspecto se han desarrollado con el paso de los años modelos dependientes de la frecuencia que permiten obtener de mejor manera los resultados de las simulaciones en estado transitorio conocidos como modelos de parámetros distribuidos que son de utilidad para el análisis de fallas o la coordinación del aislamiento en el sistema eléctrico [8].
Teniendo en cuenta los aspectos mencionados, este estudio se enfoca en obtener el modelo de parámetros distribuidos de una línea de transmisión a partir de la medición de un sobrevoltaje transitorio de maniobra. La ejecución del experimento en el sistema eléctrico conlleva muchas limitaciones y riesgos debido a los sobrevoltajes generados y la desconexión y reconexión de las líneas de transmisión, y por ello, se recurrió a un modelo de línea de transmisión a escala que funciona con 220 V en un laboratorio. De manera que en el modelo se pueden ejecutar varias veces el experimento para producir el sobrevoltaje necesario y poder determinar los parámetros de la línea en estudio.
De esta manera, este artículo técnico provee un ejemplo de la obtención de los parámetros de una línea de transmisión para que pueda ser empleado como un método alternativo para obtener los parámetros de una línea real en el sistema eléctrico cuando se obtenga un registro de un sobrevoltaje de maniobra, de manera que se mejore el modelo de aquella línea y pueda ser más acertado para los estudios en estado transitorio del sistema eléctrico al que pertenezca.
Este artículo contiene la parte práctica en la que se consiguieron los valores de entrada y salida utilizando un prototipo de laboratorio de línea de transmisión de 230 kV que tiene longitudes de línea de 100 km, 200 km y 400 km; sus valores fueron comparados con los valores teóricos y después de un estudio minucioso se sintonizan los modelos mediante algoritmos de optimización de la Herramienta Parameter Estimation de MATLAB.
PARÁMETROS DE LA LÍNEA DE TRANSMISIÓN
Para la facilidad en los cálculos de los parámetros eléctricos de cualquier línea de transmisión se efectúan simplificaciones que van a depender de la longitud de la línea; por tal motivo las líneas se clasifican en: línea corta con una longitud de hasta 80 km, línea media con una longitud comprendida entre 80 km y 240 km y línea larga con una longitud superior a 240 km [9].
Las líneas de transmisión están conformadas esencialmente por cuatro parámetros principales, los que están conectados tanto en serie como en paralelo, los parámetros que se encuentran conectados en serie son la resistencia y la inductancia formando una impedancia en serie al momento de dividirse de manera uniforme a lo largo de la línea; y los parámetros que se encuentran conectados en paralelo son la capacitancia y la conductancia. Cabe hacer mención que en las líneas de disposición aérea la conductancia en gran parte de los casos es despreciada [10], [11].
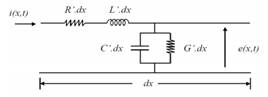
La línea de transmisión con sus respectivos parámetros eléctricos queda modelada como se representa en la Fig.1.
Siendo:
R': Resistencia en Ω/km.
L': Inductancia en H/km.
C': Capacitancia en F/km.
G': Conductancia en µS/km.
Modelos de la línea de transmisión
Dentro de los diferentes modelos existentes en la bibliografía se pueden encontrar los modelos de parámetros concentrados constantes como el modelo PI nominal y los modelos de parámetros distribuidos como el de Bergeron, estos modelos fueron los utilizados en este artículo [3].
Modelo PI nominal
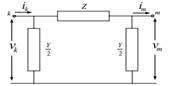
Este modelo es el que está destinado a utilizarse en simulaciones de estado estacionario de las líneas cortas a una frecuencia nominal o frecuencia de la red. El circuito PI nominal para la línea de transmisión se representa en la Fig. 2. Las ecuaciones que hacen relación a las corrientes y voltajes en cada extremo de la línea se presentan en [3].
l = Longitud de la línea en km.
Z= Impedancia de la línea de transmisión.
Y= Admitancia de la línea de transmisión.
Este modelo presentado no suele tener tanta veracidad para fenómenos determinados por sobrevoltajes por maniobra y por descargas atmosféricas [3].
Modelo de Bergeron
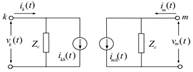
Es un modelo elaborado por Hermann Dommel, se fundamenta en fenómenos de difusión de ondas viajeras presentes en la línea de transmisión, usando parámetros constantes y distribuidos a lo largo de la línea L’ y C'. En la Fig. 3 se presenta el modelo mencionado y las ecuaciones que hacen relación a las corrientes y voltajes en cada extremo de la línea se presentan en [3].
Métodos de optimización no lineales en MATLAB-Simulink usados para optimizar
En la actualidad existen muchos tipos de métodos que proporcionan la optimización de funciones establecidas mediante un ajuste de curvas. En este artículo para la optimización de las respectivas funciones se tomó como base la utilización de los métodos que facilita el software MATLAB-Simulink en su herramienta Parameter Estimation, los mismos que se pueden referir con mayor detalle en [13].
METODOLOGÍA
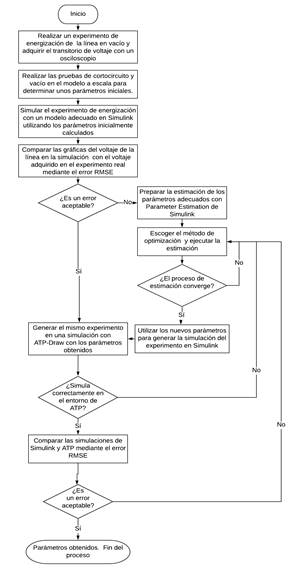
Para realizar la estimación de los parámetros del modelo a escala de línea de transmisión se procedió según el diagrama de flujo de la Fig. 4.
Los componentes necesarios para este procedimiento se describen a continuación.
Modelo de simulación
Se utilizó el modelo de parámetros distribuidos existente en la biblioteca de MATLAB-Simulink, porque ha sido comprobado con validez tanto teórica como práctica, además se adecúa al modelos a escala de línea de transmisión trifásica que se tiene en el laboratorio y consigue tratar la mayoría de parámetros eléctricos encontrados en las pruebas de laboratorio, el modelo denominado como “Distributed Parameters Line”, que considera a la línea trifásica con parámetros distribuidos [14].
Modelo a escala de laboratorio
Se utilizó un prototipo de línea de transmisión trifásica de 230 kV con la que se puede trabajar con diferentes longitudes para el análisis; específicamente se usó para 100 km, 200 km y 400 km y está disponible en el Laboratorio de Máquinas Eléctricas de la Escuela Politécnica Nacional.
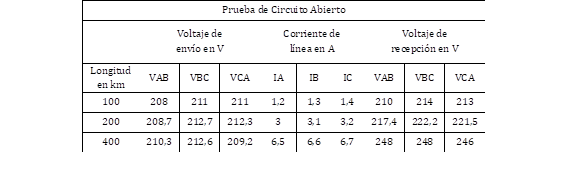
Se efectuaron pruebas de corto circuito y circuito abierto en donde se tomaron datos de voltajes de envío y de recepción, además de corrientes de envío y de recepción para cada longitud de la línea. Esta información era necesaria para poder obtener los valores de los parámetros eléctricos de la línea de transmisión y compararlos con los parámetros que corresponden a una línea de transmisión de 200 km, que se encuentran en el documento en el que se detalla la construcción de dicha línea en [15].
Para las líneas de transmisión de 100 km y 200 km se utilizan las ecuaciones (1), (2), (3), (4), (5), (6) y (7), siendo VS, IS los voltajes y corrientes de envío y VR, IR los voltajes y corrientes de recepción.
Para la línea de transmisión de 400 km se utilizan las ecuaciones (1), (2), (3), (8), (9), (10) y (11).
Para obtener los parámetros de secuencia cero se hace uso de las ecuaciones (12), (13), (14), (15), (16), (17) y (18) según [16].
Generación del evento transitorio de voltaje
El evento transitorio de voltaje que se efectúa es el de energización en vacío de la línea de transmisión trifásica, para lo cual se hace uso de un interruptor trifásico. Este elemento es conectado entre la fuente de alimentación y la línea de transmisión y para efectuar el evento se cierra de manera manual energizando el circuito y produciendo en ese instante de energización el transitorio de voltaje. El circuito implementado se presenta en la Fig. 5.
Se escogió una maniobra de energización de una línea por la sencillez en su ejecución. La forma de la onda de sobrevoltaje depende del instante de tiempo en el que se cierra el interruptor que energiza la línea; la maniobra no posee un control de tiempo de cierre del interruptor ya que es manual, y en general mientras más cercano sea el tiempo de cierre del interruptor al tiempo de cruce por cero de la onda de voltaje de la fuente se produce un sobrevoltaje menor en la línea de transmisión. Observando una serie de experimentos se consideró que mientras más cercano sea el tiempo de cierre al tiempo de un pico de la onda de voltaje de la fuente el sobrevoltaje en la línea era mayor y más evidente, y en la simulación que se realizaría posteriormente se podía modificar fácilmente el tiempo del cierre del interruptor hasta que el sobrevoltaje simulado tenga la misma fase que el sobrevoltaje medido en el experimento, al ser más pronunciado el transitorio de voltaje se podría estimar de mejor manera los valores de los parámetros del modelo de la línea que tienen mayor influencia en la forma de la onda, por ello se proceden a realizar varios de estos eventos hasta conseguir un transitorio pronunciado que tenga una forma de onda que sea evidente para poder realizar el trabajo propuesto. Las maniobras de energización se las realiza para las tres longitudes de línea que son: 100 km, 200 km y 400 km.
La adquisición de datos se realizó mediante la obtención de las formas de onda de las curvas de entrada y curvas de salida usando un osciloscopio digital por medio de dos de sus canales, estos datos se recopilaron digitalmente para su posterior utilización.
Estimación de parámetros
Las pruebas efectuadas de circuito abierto y de corto circuito correspondientes, sirvieron para calcular los parámetros eléctricos iniciales de las líneas de transmisión según lo indicado en la sección 3.2 y así conseguir las señales de las curvas de voltaje a las salidas de cada línea con la asistencia del osciloscopio digital.
Los datos fueron procesados usando MATLAB-Simulink, y se modeló la línea de transmisión con su respectiva perturbación, el modelo está conformado por una fuente de voltaje trifásico alterno que proporciona el voltaje adecuado, la línea de transmisión trifásica de parámetros distribuidos, un interruptor que servirá para realizar los eventos transitorios de voltaje por maniobra en el sistema, y un medidor de voltaje de salida que indicará la cantidad de voltaje que se obtiene y la forma de la señal.
Una vez inicializados los parámetros eléctricos de la línea de transmisión se procede con la simulación y se obtienen como resultado dos curvas; una que representa a la curva obtenida mediante la simulación con las condiciones iniciales, la misma que se utilizará en una optimización para la estimación de los parámetros eléctricos y la otra que es la curva obtenida de forma experimental en el laboratorio, mediante las mediciones descritas en 3.3.
La sintonización de parámetros se efectúa con la ayuda de la herramienta de Estimación de Parámetros de Simulink. Para detalles de cómo usar esta herramienta de estimación y los diferentes métodos de optimización no lineales que existen referirse a [17].
RESULTADOS Y DISCUSIÓN
Cálculo de los parámetros eléctricos de secuencia positiva en base a las pruebas de circuito abierto y de corto circuito
En este caso se dispone de dos líneas medias de longitudes correspondientes a 100 km y 200 km; y una línea larga de 400 km. Los resultados de las pruebas de vacío efectuadas se presentan en la Tabla 1 y de las pruebas de cortocircuito, en la Tabla 2. Para obtener los parámetros de la línea se procede según la Sección 3.2 y se obtienen los resultados iniciales presentados en la Tabla 3.
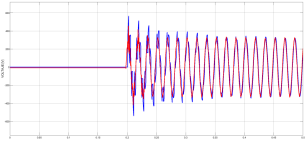
Se ejecuta la simulación del evento transitorio de voltaje y la Fig. 6 representa los resultados iniciales de las curvas experimental (roja) y simulada (azul) en el caso de la línea de 400 km para poder aplicar a estas señales los diferentes métodos de optimización mediante la herramienta Parameter Estimation.
Sintonización de los parámetros eléctricos de la línea de transmisión trifásica mediante el evento transitorio de voltaje
En la herramienta Parameter Estimation de MATLAB se realizan las sintonizaciones de los parámetros con los diversos métodos de optimización que posee que son: Levenberg-Marquardt, Región De Confianza Reflectivo, Búsqueda Simple, Programación Cuadrática Secuencial y Conjunto Activo. En la Fig. 7 se observa como ejemplo el ajuste realizado por el método Levenberg-Marquardt para que la señal simulada sea similar a la señal experimental para el caso de la línea de 400 km.
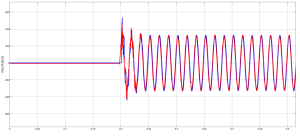
Figura 7: Voltaje en la línea de transmisión trifásica de 400 km después de la estimación de parámetros por el método Levenberg-Marquardt, Experimental (roja) vs Simulación (azul)
En la Tabla 4 se encuentran los resultados de parámetros sintonizados al aplicar los diferentes métodos de optimización. Los resultados del método Levenberg Marquardt indican que existe en general una variación muy pequeña en gran parte de los parámetros eléctricos de secuencia positiva y cero lo que produce un porcentaje de diferencia muy pequeña, siendo la excepción la resistencia de secuencia positiva la cual posee un porcentaje de diferencia grande.
En los resultados obtenidos al aplicar el método Región de Confianza Reflectivo se evidencia que existe una variación de los parámetros eléctricos de secuencia positiva con un porcentaje de diferencia pequeño, siendo la más considerable de la resistencia de secuencia positiva, para los parámetros eléctricos de secuencia cero no existe variación por lo que posee un porcentaje de diferencia nula en todos los casos.
El método de Búsqueda Simple expresa los resultados con un porcentaje de diferencia elevado tanto para los parámetros de secuencia positiva y cero, siendo la más llamativa para la inductancia de secuencia positiva ya que tiene un valor considerable de variación.
Para el algoritmo Programación Cuadrática Secuencial se tienen variaciones para los parámetros eléctricos de secuencia positiva siendo estas las de mayor porcentaje de diferencia, teniendo para la inductancia un valor muy elevado. En mención a los parámetros eléctricos de secuencia cero las variaciones son prácticamente nulas por lo cual no existe porcentaje de diferencia en estos casos.
El método Conjunto Activo presenta los resultados con un porcentaje de diferencia nulo, prácticamente en todos los parámetros eléctricos debido a que dicho método no ejecuta muchas iteraciones haciendo que la inductancia, resistencia y capacitancia tanto para secuencia positiva y cero no sufran gran variación.
Selección del método más apropiado para la sintonización de parámetros eléctricos de líneas de transmisión trifásicas de diferentes longitudes según el error cuadrático medio
En las pruebas realizadas para la obtención de los parámetros eléctricos originales de la línea de transmisión se presentan errores ya sea por apreciación humana o por los errores de los equipos de medición.
Para escoger el método de optimización no lineal adecuado, en primera instancia se procedió a tomar como base el error cuadrático medio entre las curvas simuladas y reales de voltaje de las líneas de transmisión propuestas. Luego, con la ayuda del software ATP/ATPDraw se puede corroborar si los parámetros seleccionados son los adecuados, ya que este programa proporciona mayor confiabilidad al momento de simular transitorios electromagnéticos, en este caso de la línea de transmisión con los parámetros estimados; teniendo así los siguientes resultados.
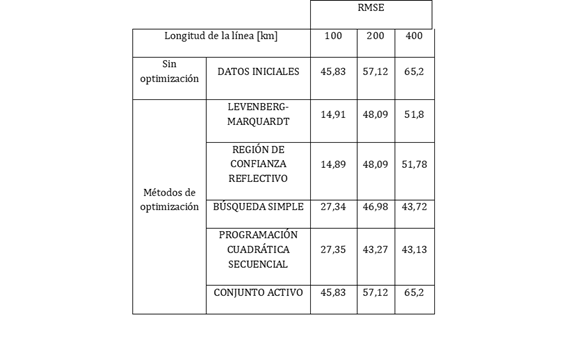
En la Tabla 5 se presenta el error cuadrático medio RMSE de la señal simulada.
Tabla 4: Parámetros eléctricos estimados con diferentes métodos para la línea de transmisión trifásica
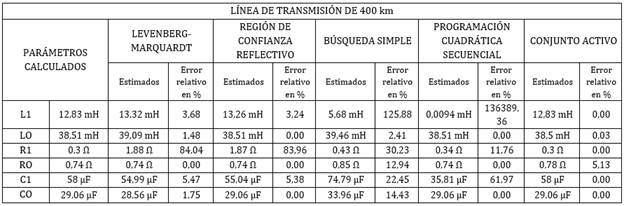


Tomando como ejemplo la línea de 400 km, se observa que con los parámetros calculados inicialmente el valor RMSE es de 65,2. Una vez calculado este error en cada uno los métodos aplicados para la estimación de parámetros se pueden evidenciar que existe un algoritmo que logra reducirlo a un valor mínimo de 43,13 siendo este el de Programación Cuadrática Secuencial. Sin embargo, al utilizar los parámetros obtenidos por el método de Programación Cuadrática Secuencial y simularlos en el modelo de Bergeron de ATP la simulación no pudo ser ejecutada mientras que en Simulink la simulación funcionaba correctamente.
En la Tabla 4 se puede apreciar que el método de Programación Cuadrática Secuencial difiere en gran medida en el valor de la inductancia de secuencia positiva L1, el método obtiene un valor de L1 muy pequeño comparado con los otros métodos y al usar este valor en ATP se producen errores debido a que el valor del parámetro es irreal. Se puede apreciar entonces que a pesar de que Simulink realice esta simulación con ese valor no necesariamente es una simulación correcta, también se aprecia que el método con el menor RMSE no necesariamente es el mejor método para obtener los parámetros de esta línea. Se puede decir que para la sintonización de parámetros eléctricos de una línea de transmisión trifásica de 400 km no es recomendable aplicar el método Programación Cuadrática Secuencial. Y para comprobar que los parámetros obtenidos en Simulink pueden utilizarse se ponen a prueba en una simulación similar en el software ATP en todos los casos analizados.
Las simulaciones realizadas en ATP de las líneas de transmisión trifásicas con parámetros eléctricos sintonizados a diferentes longitudes sirven para poder llegar a la conclusión que no es siempre aconsejable aplicar métodos de optimización no lineal con el criterio de selección del menor error cuadrático medio, ya que estos algoritmos proporcionan ciertos valores de parámetros eléctricos muy pequeños lo que significaría que físicamente no son muy reales. En efecto, para poder seleccionar el método de optimización no lineal adecuado para la sintonización de los parámetros eléctricos de las líneas de transmisión analizadas se debería escoger parámetros sintonizados que no estén muy lejos de los parámetros calculados y esto se logra identificar con la ayuda del error relativo obtenido entre los parámetros calculados y los parámetros estimados; evidenciando si estos son correctos o no con la respectiva simulación en el programa ATP. El procedimiento para las líneas de 100 km y 200 km es el mismo que se encuentra detallado para la línea de 400 km. Se puede decir que, para la sintonización de parámetros eléctricos de una línea de las líneas de transmisión trifásica de 100, 200 y 400 km según la Tabla 4 donde se analiza y escoge el método de optimización con menor porcentaje de diferencia para la sintonización de parámetros eléctricos; se sugiere aplicar los algoritmos Levenberg Marquardt y Región de Confianza Reflectivo.
Las simulaciones efectuadas en ATP con los parámetros eléctricos ya sintonizados según los algoritmos Levenberg Marquardt y Región de Confianza Reflectivo ayudan a concluir que para la sintonización de parámetros eléctricos de las diferentes líneas de transmisión es muy recomendable aplicar los métodos señalados, ya que se ha verificado cada uno de estos con las simulaciones efectuadas en el ATP.
Haciendo referencia al método Conjunto Activo que evidentemente posee el menor porcentaje de diferencia no es considerado como muy aplicable para la sintonización de parámetros ya que este algoritmo realiza muy pocas iteraciones lo que produce que los parámetros no se ajusten del mismo modo como lo hacen los métodos ya expuestos que son el Levenberg Marquardt y Región de Confianza Reflectivo.
El procedimiento para las líneas de 100 km y 200 km es el mismo como se encuentra detallado para la línea de 400 km. La comparación se realiza para evidenciar si las señales simuladas tanto en MATLAB como en ATP son parecidas o si a su vez tienen alguna variación. Se presenta un ejemplo para la línea de transmisión trifásica de 400 km en las Fig. 8 y Fig. 9.
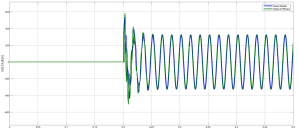
Figura 8: Voltaje en la línea de transmisión trifásica de 400 km después de la estimación de parámetros por el método Levenberg Marquardt, ATP (verde) vs MATLAB (azul)
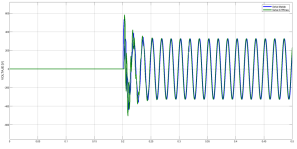
Figura 9: Voltaje en la línea de transmisión trifásica de 400 km después de la estimación de parámetros por el método Región de Confianza Reflectivo, ATP (verde) vs MATLAB (azul)
Finalmente; al realizar las simulaciones en los dos paquetes computacionales mencionados se puede observar que las señales obtenidas a las salidas de las líneas de transmisión trifásicas estudiadas son semejantes por lo que se puede aseverar que la sintonización de los parámetros eléctricos mediante la herramienta Parameter Estimation del Simulink es aplicable, especialmente con el uso de los métodos Levenberg Marquardt y Región de Confianza Reflectivo.
CONCLUSIONES Y RECOMENDACIONES
Para la simulación de la línea de transmisión se utilizó el modelo de parámetros distribuidos, ya que se lo consideró adecuado porque éste responde a perturbaciones como fenómenos transitorios producidos en la apertura y cierre de una línea de transmisión, dicha aseveración fue comprobada al efectuar las simulaciones en las cuales proporcionó resultados muy cercanos a la realidad. El modelo detallado es fundamental ya que ayudó a cumplir con uno de los objetivos del estudio que era estimar los parámetros de la línea ante la presencia de un transitorio de voltaje.
Al revisar los resultados obtenidos se puede decir que se cumple con el objetivo de estimar los parámetros de líneas de transmisión de una manera no tradicional, pudiendo tener una aplicación directa en las líneas de transmisión del Sistema Nacional de Transmisión en donde seria óptimo disponer de instrumentos que proporcionen información de las curvas de fenómenos transitorios, y así aprovechar estas señales y realizar la respectiva estimación de los parámetros.
El error cuadrático medio no siempre va a ser un indicador adecuado para poder seleccionar qué tipo de método de optimización no lineal es el mejor para realizar estimación de parámetros; ya que se pudo comprobar que el método de Programación Cuadrática Secuencial que tenía el menor error cuadrático medio en la línea de 400 km obtenía unos parámetros que no generan las simulaciones en otro programa que no sea Simulink como en el caso de ATP que se utiliza mucho para la simulación de transitorios de voltaje; ya que estos parámetros pueden ser muy pequeños por lo que se les considera inexistentes. Por ello en este trabajo se escogió los métodos que no generaban conflictos en las simulaciones con ATP junto a la observación de que su error RMSE y error relativo de parámetros sea aceptable.