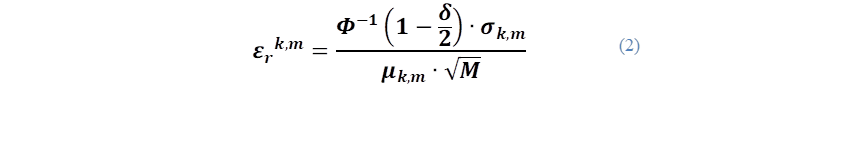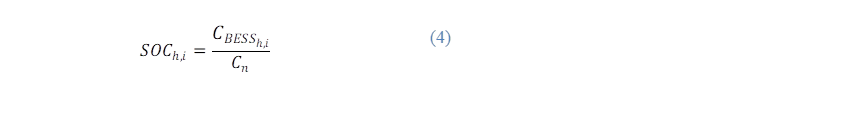INTRODUCCIÓN
La instalación de sistemas de almacenamiento de energía (SAE) de gran capacidad e integrados en la red pone de relieve el surgimiento de un nuevo segmento de investigación, en el cual es necesario contar con soluciones específicas y apropiadas para gestionar y controlar estos sistemas, de forma optimizada para cada una de las funcionalidades requeridas.
La característica fundamental de la energía, para que pueda ser de utilidad, es que se encuentre a disposición del usuario cuando sea requerida. Así, la necesidad de almacenamiento de energía viene dada por el desfase natural que existe entre la generación basada en fuentes renovables intermitentes (e.g. fotovoltaica PV) y el consumo de la energía, cuyo desfase se debe a la aleatoriedad de producción de estas fuentes y a los ciclos de consumo de energía, los cuales, en general, son de carácter estocástico. Además, la existencia de picos de consumo de energía que deben ser cubiertos a lo largo del día podrían provocar un sobredimensionado enorme e innecesario de plantas de generación para producir toda la energía, perdiendo la eficiencia en la producción. Este aspecto es de peculiar importancia en las microrredes.
Actualmente, los SAE basados en sistemas de almacenamiento de energía usando baterías (BESS) están tomando gran importancia por su variedad de aplicaciones, muchas más que cualquier otro tipo de sistema de almacenamiento, debido en parte, a que son el método más antiguo para almacenar energía. Las baterías son células recargables que almacenan y devuelven energía eléctrica gracias a reacciones químicas en su interior. Son sus componentes los que determinan sus cualidades, tales como: capacidad de carga y descarga, capacidad de almacenamiento, estado de carga (SOC), densidad de energía o ciclabilidad. Entre sus principales inconvenientes se encuentra su coste de almacenamiento, el volumen que ocupan (y su peso), su baja ciclabilidad y su vida útil. Existen algunos estudios que consideran las características anteriormente mencionadas, los cuales, de forma general, se describen a continuación.
En [1] se analizan diferentes aplicaciones de los SAE, los cuales, por ejemplo, pueden usarse dentro de un mercado de energía para obtener ganancias al cargar las baterías durante períodos de precios bajos de energía y descargar cuando los precios son altos. Además, los sistemas de almacenamiento de energía pueden usarse para mantener el voltaje en la red de distribución, para reducir el pico de la curva de demanda y reducir la potencia máxima en las líneas de transmisión. Sin embargo, una de las aplicaciones más prometedoras es el control primario de frecuencia [1], correspondiente al primer nivel de respuesta de frecuencia después de un desbalance de generación-carga. Los sistemas de almacenamiento pueden cambiar su potencia despachada más rápido que las plantas de generación, como, por ejemplo, las centrales hidroeléctricas que necesitan primero estabilizar la presión del agua antes de aumentar la potencia [2]. Dado que los sistemas de almacenamiento se pueden cargar o descargar por completo en cortos períodos de tiempo, es necesario que los algoritmos de control mantengan el estado de carga (SOC) entre ciertos límites para garantizar la disponibilidad total del control de frecuencia primaria.
En [3], se presenta un método para dimensionar sistemas de almacenamiento de energía para regulación primaria de frecuencia, considerando los límites de los estados de carga de las baterías y las resistencias de emergencia para disipar el exceso de energía. En cambio, en [4] se propone una nueva metodología para corregir el punto de trabajo de los sistemas de almacenamiento; mientras que, en [5] y [6] se desarrolla el modelo de control incluyendo la rentabilidad y degradación. En estas referencias, se sugiere un enfoque multinivel para limitar óptimamente los estados de carga de los SAE. Un sistema similar se describe en [7], donde también se muestran las mediciones de eficiencia y auxiliares.
Un aspecto importante a considerar dentro de la gestión de BESS es su potencial contribución para incrementar la energía firme de microrredes donde existe considerable penetración de fuentes intermitentes de energía, como por ejemplo generación fotovoltaica (sistemas PV-BESS) [8]. En estos casos, el BESS tiene como propósitos: i) incrementar la capacidad de generación del sistema PV (mejorar la energía firme de la microrred) y ii) mejorar la regulación de frecuencia. En este tipo de configuración, es necesario evaluar el impacto del PV-BESS, tanto en operación de estado estacionario como en estado dinámico. En el primer caso, se vuelve indispensable considerar la estocasticidad de los estados operativos causada por la naturaleza intermitente del recurso primario, la cual puede ser evaluada mediante flujos de potencia probabilísticos (PPF por sus siglas en inglés) [9]. En este tipo de evaluación, la definición de los modelos estocásticos de las variables de entrada (funciones de distribución de probabilidad - PDF por sus siglas en inglés) constituye un aspecto fundamental que debe ser adecuadamente determinado.
A este respecto, se requiere incluir (a más de los modelos estocásticos asociados con los recursos intermitentes: irradiación solar, velocidad del viento, temperatura, etc.) un modelo estocástico apropiado del SOC del BESS, el cual deberá interactuar con su requerimiento de carga y descarga. En este sentido, es posible encontrar en la literatura varias propuestas para estimar el SOC de una batería, las cuales se pueden clasificar en cuatro tipos generales: i) mediciones directas, ii) conteo de Coulombs o sistemas “book-keeping”, iii) sistemas adaptivos y iv) métodos híbridos [10] [11] [12]. No obstante, todas estas propuestas están orientadas a determinar un indicativo del estado de carga actual de la batería, más no brindan un modelo estocástico capaz de ser incluido en una simulación de PPF.
Sobre la base de lo mencionado, el presente trabajo presenta una novedosa propuesta metodológica que permite determinar el modelo estocástico del SOC de un BESS implementado con un generador fotovoltaico (sistema PV-BESS) que podrá ser usado en la evaluación horaria de PPF de una microrred. Esta metodología se basa en los resultados estocásticos de generación horaria del PV sin considerar la interacción con el BESS, los cuales son usados para definir las PDF del SOC del BESS considerando diferentes escenarios probabilísticos. Posteriormente, se aplica el modelo determinado en la solución de un PPF de una microrred, cuya estructura también es presentada.
El resto de este documento está organizado de la siguiente manera. En primer lugar, se presenta un marco conceptual sobre microrredes, baterías y flujos probabilísticos. Posteriormente se despliega la propuesta metodológica para evaluar PPF en microgrids y para determinar el modelo estocástico del SOC de un sistema PV-BESS, luego se muestra la aplicación a una red de prueba formada por una red de potencia principal y una microrred funcionando en modo “conectada a la red”. Finalmente se presentan las conclusiones y recomendaciones.
MARCO CONCEPTUAL
Microrredes
Las microrredes son sistemas eléctricos de medio y bajo voltaje que genera energía eléctrica usando, en su mayoría, fuentes renovables no convencionales (eólico, fotovoltaico, biomasa, etc.); además, se componen de motores de combustión interna (energía complementaria) y equipos de almacenamiento (baterías de ion litio, supercondensadores, pilas de hidrógeno, etc.).
Estas microrredes se ubican cerca de la demanda con la finalidad de reducir la distancia física/eléctrica entre la generación y carga, mejorando la confiabilidad, disminuyendo las pérdidas por transmisión y reduciendo las emisiones de carbono [13]. Otra de las principales ventajas es su capacidad de operar de forma aislada o conectada al sistema eléctrico de potencia (SEP).
La microrred debe ser capaz de desconectarse y reconectarse de la red, tanto en estados operativos normales como en emergencia. La capacidad de operación aislada y autónoma repercute favorablemente en la calidad y la fiabilidad de suministro eléctrico, dado que el consumidor final tendrá garantizada la continuidad de suministro, a pesar de discontinuidades en el suministro eléctrico asociadas a fallas y mantenimiento [13]. La reconexión de la microrred y SEP se realiza, siempre que se cumpla con los rangos de voltaje, frecuencia y ángulo de fase establecido por las regulaciones de operación de cada sistema o lo especificado en el estándar ANSI C84.1-2006 [14].
Dentro de las tecnologías más utilizadas en las microrredes se encuentran la fotovoltaica y la eólica, que se caracterizan por no proporcionar energía firme debido a la intermitencia del recurso primario. Estas intermitencias pueden ser complementadas con BESS.
Baterías (BESS)
La batería eléctrica es un dispositivo que consta celdas electroquímicas, las cuales tienen la capacidad de convertir la energía química en energía eléctrica y viceversa [15]. En el contexto de microrredes, la función principal del BESS es almacenar energía cuando haya excedentes (bajos costos) y utilizarla cuando las fuentes renovables no generen lo suficiente.
La planificación de la expansión y operación de microrredes definen el coste, la capacidad de almacenamiento, vida útil y tamaño de las tecnologías de almacenamiento. Para ello, se definen variables de diseño que determinan las condiciones de operación de las baterías, cuyos valores se caracterizan por un comportamiento estocástico producto de la aleatoriedad de las fuentes renovables no convencionales y demandas conectadas a la microrred. A continuación, se describe las principales variables de diseño que caracterizan los valores nominales y máximos de la batería [16]:
Capacidad nominal (Amperios-hora): es el total de Amperios-horas disponibles cuando la batería se descarga. La capacidad se calcula multiplicando la corriente de descarga (en amperios) por el tiempo de descarga (en horas).
Profundidad de descarga (Depth of Discharge - DOD) (%): es el porcentaje de la capacidad total de la batería que es utilizada en el proceso de descarga. Cuanto mayor es la profundidad de descarga, menor es el número de ciclos que se puede obtener de ella.
Energía nominal (Wh): es la capacidad total de energía disponible cuando la batería se descarga, desde 100 % hasta la tensión de corte. La energía se calcula multiplicando la potencia de descarga (en vatios) por el tiempo de descarga (en horas). La energía disminuye al aumentar la tasa de descarga.
Tensión de corte (Cut-off Voltage): es la tensión mínima permitida, cuyo valor, generalmente, define el estado “vacío” de la batería.
Estado de carga (State of Charge - SOC) (%): es la capacidad actual de la batería representada como porcentaje de la capacidad máxima. El SOC de una batería se define como la relación entre su capacidad actual (C(t)) y la capacidad nominal ( 𝑪 𝒏 ). La capacidad nominal representa la cantidad máxima de carga que se puede almacenar en la batería [11].
A continuación, se describen la clasificación de los métodos matemáticos de estimación del SOC [11] [12]:
Mediciones directas: este método utiliza las propiedades físicas de la batería como el voltaje y la impedancia de la batería. Se han empleado muchos métodos directos diferentes, como: el método de voltaje de circuito abierto, el método del voltaje terminal, el método de medición de impedancia y el método de espectroscopia de impedancia.
Conteo de Coulombs o sistemas “book-keeping”: este método utiliza la corriente de descarga como entrada y la integra a lo largo del tiempo para calcular el SOC. Se han empleado dos tipos de métodos: 1) conteo de Coulomb y, 2) conteo de Coulomb modificado.
Sistemas adaptivos: son métodos que pueden ajustar automáticamente el SOC para diferentes condiciones de descarga. Los métodos desarrollados incluyen redes neuronales, métodos de lógica difusa, minería de datos (support vector machine) y filtros de Kalman.
Métodos Híbridos: los modelos híbridos se benefician de las ventajas de cada método de estimación de SOC y permiten un rendimiento de estimación globalmente óptimo. La literatura muestra que los métodos híbridos generalmente producen una buena estimación de SOC, en comparación con los métodos individuales.
Todas estas metodologías están orientadas a determinar un indicativo del estado de carga actual de la batería, más no brindan un modelo estocástico capaz de ser incluido en una simulación de PPF.
Flujos de Potencia Probabilísticos (PPF)
El problema de flujo de potencia consiste en determinar las condiciones de operación en estado estacionario del sistema de potencia. Con los valores de la carga (demanda) en las barras de consumo y la potencia suministrada por las unidades de generación, el objetivo es obtener los voltajes (magnitud y ángulo) de todos los nodos del sistema y la potencia activa y reactiva que fluye a través de cada vínculo de la red. Matemáticamente, el problema de flujo de potencia puede ser representado como una función vectorial en donde el vector de las variables de entrada consiste en la inyección de potencia en cada barra, excepto en la barra oscilante o slack; y el vector de variables de salida se compone de todos los voltajes de las barras (excepto el voltaje en la barra oscilante) y de todos los flujos de potencia complejos.
El concepto de flujo de potencia probabilístico viene dado desde la consideración de la incertidumbre intrínseca de conocer el vector de entrada. Esta incertidumbre se transfiere a la solución del vector de las variables de salida a través de la función del vector. El objetivo del análisis del flujo de potencia probabilístico es caracterizar el comportamiento aleatorio de la solución a partir de la información estadística sobre cada factor o variable de entrada modelada de forma estocástica como, por ejemplo, la velocidad del viento, la irradiación solar, la temperatura, entre otros factores que afectan a la energía generada por las centrales de generación de naturaleza intermitente a cada instante del día [9] [17].
El método de Monte Carlo puede ser usado para evaluar, de forma probabilística, los flujos de potencia, tomando en cuenta la variabilidad de los datos de entrada (i.e. carga, recurso primario, entre otros). Es un proceso repetitivo, en el cual se perturban aleatoriamente los datos de entrada alrededor de un punto medio y dentro de un intervalo de varianza que probablemente contiene el valor más esperado. Para esto, las variables de entrada deben ser representadas con un adecuado modelo estocástico.
Los resultados de cada flujo son almacenados para el posterior análisis, luego de cumplir con un número suficiente de iteraciones mediante los cuales el problema se encuentre bien representado. Así, este número de iteraciones puede ser definido, por ejemplo, a través del criterio de parada presentado en (2), el cual usa un concepto de error relativo ((r) probabilístico que depende de los resultados estadísticos obtenidos en la(s) variable(s) de salida [18].
donde 𝜱 −𝟏 es la función inversa de distribución normal estándar, 𝝁 𝒌,𝒎 es la media de la variable k de salida simulada con m datos, 𝝈 𝒌,𝒎 es la desviación estándar de la variable k simulada con m datos, M es el número de iteraciones y 𝜹 es el nivel de confianza (que suele ser de 1% o 5%).
Finalmente, las variables de salida son representadas mediante distribuciones o histogramas y pueden ser usadas para interpretar de forma estadística o probabilística el comportamiento del sistema en análisis.
PROPUESTA METODOLÓGICA
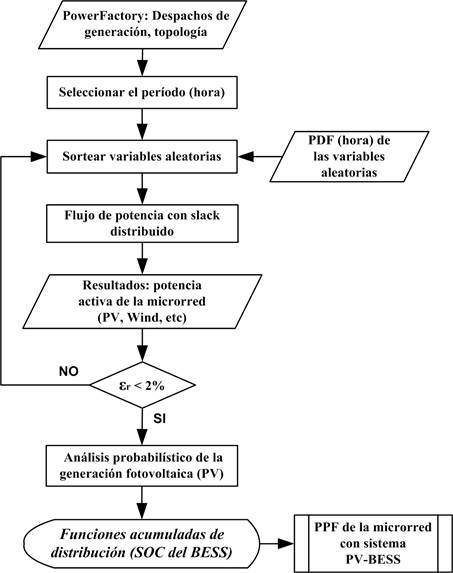
En la Fig. 1 se presenta el esquema de la metodología propuesta, la cual permite el análisis probabilístico del SOC de un BESS que opera de forma conjunta con un sistema PV (PV-BESS). Para ello, se desarrolla una herramienta computacional que enlaza los programas de DIgSILENT PowerFactory y Python con el propósito de potenciar las ventajas de simulación, análisis matemático y scripting de estos aplicativos.
A continuación, se describen los principales pasos de la propuesta metodológica:
En DIgSILENT PowerFactory se modela el sistema eléctrico de potencia incluyendo topología de la red de transmisión y disponibilidad de las unidades de generación.
Se selecciona el periodo de tiempo (hora). En este estudio se consideran escenarios operativos diarios para las 24 horas.
Se sortean las variables aleatorias a partir de PDFs ingresadas como dato. Específicamente, se sortean las variables primarias estocásticas de las fuentes de energía renovables intermitentes, tales como: velocidad del viento, temperatura ambiente e irradiación solar. Además, se considera la aleatoriedad de la demanda de la microrred por medio de PDFs Normales. En esta etapa se deben especificar las premisas operativas de despacho y preventa de energía entre el SEP y la microrred.
Se simula un flujo de potencia (PF) con slack distribuido con la finalidad de despachar la potencia activa y reactiva entre los generadores con capacidad de regulación. En este caso, estos generadores absorben las variaciones de carga e intermitencia de las fuentes de energía renovables mediante una matriz de sensibilidad de flujos, permitiendo simular una operación más real del sistema. Es importante destacar que, este paso también podría ser realizado por un flujo óptimo de potencia considerando los costos variables de producción.
Se obtienen los resultados correspondientes a la generación de potencia activa de la microrred (de forma particular es necesario obtener la potencia inyectada por el sistema PV que operará en conjunto con el BESS, 𝑃 𝑃𝑉 ), el voltaje en el punto de conexión principal y la generación de la red principal.
Se determina el criterio de parada de la simulación de Montecarlo correspondiente al Error Relativo ((r) para un nivel de confianza del 1%. En caso de que este valor no sea menor al 2%, se sortean nuevamente las variables aleatorias (Paso 3).
Cuando (r<2%, se realiza el análisis probabilístico de la generación fotovoltaica mediante la determinación de 100 escenarios de probabilidad de la potencia inyectada por PV para cada hora, a partir de los datos almacenados en el paso 5. Esto permite estructurar una matriz 𝑃 𝑃𝑉 ℎ,𝑖 , donde i representa el i-ésimo escenario probabilístico relacionado con la probabilidad 𝑝 𝑖 ; mientras que, h representa la hora del día. Posteriormente, se determina la matriz de carga probabilística del BESS ( 𝐶 𝐵𝐸𝑆𝑆 ℎ,𝑖 ) considerando el criterio operativo de carga del BESS y sus limitaciones operativas (mínimo estado de carga, 𝐶 𝑆𝑂𝐶 𝑚𝑖𝑛 ). Para este caso de estudio, se consideran las siguientes premisas operativas del sistema PV-BESS:
Con el propósito de maximizar los ingresos por venta de energía, el BESS es operado de tal forma que pueda generar entre las 19:00 y las 22:59. Este período representa las 4 horas de consumo pico (T), luego de la pérdida de generación fotovoltaica (donde la tarifa es la más alta).
Sobre la base de la premisa anterior, la generación del PV se usa, en primera instancia, para cargar el BESS y los posibles excedentes se venden a la red.
A partir de estas premisas, la matriz 𝐶 𝐵𝐸𝑆𝑆 ℎ,𝑖 se determina con la siguientes expresiones:
Nota: ∆𝑡 representa el intervalo entre cada período de tiempo, en este caso 1 hora.
El SOC queda determinado de la siguiente manera:
Finalmente, se determinan las PDFs acumuladas (CDF, por sus siglas en inglés) del SOC, que definen el comportamiento de carga del BESS, como una función discreta de la siguiente manera:
Las 𝐶𝐷𝐹 𝑆𝑂𝐶 ℎ sirven como datos de entrada para realizar PPF considerando dentro de la microrred el sistema híbrido fotovoltaico con baterías (PV-BESS).
RESULTADOS DE SIMULACIONES
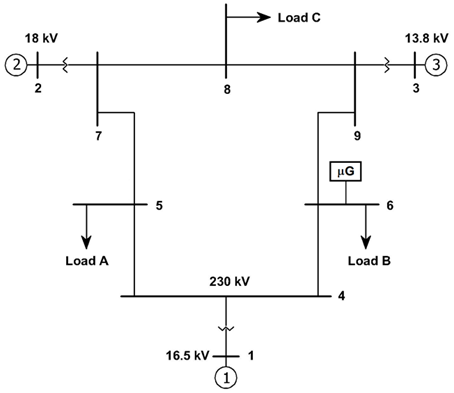
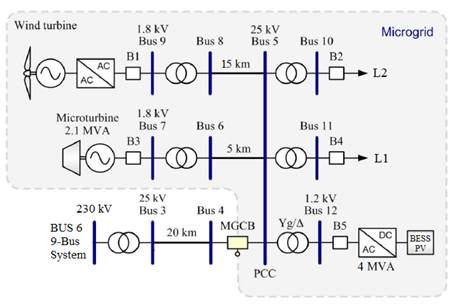
La metodología propuesta se aplica a un sistema de potencia de prueba estructurado por una red principal (la Red de Prueba WSCC de tres máquinas y nueve barras [19]) y una microrred que se conecta en la “Barra 6” de la red principal, como se muestra en la Fig. 2 y en la Fig. 3, respectivamente. Este sistema es implementado en DIgSILENT PowerFactory.
En la microrred existen tres generadores, de los cuales uno es térmico sincrónico (micro-turbina de gas) de 2.1 MVA y factor de potencia 0.96 nominales, y los otros dos son renovables de generación intermitente (un fotovoltaico de 4 MW y un eólico de 2 MW). Junto al fotovoltaico se instala un BESS (sistema PV-BESS) de 3.5 MW de capacidad máxima y 14 MWh de energía (con una autonomía de 4 horas), con un SOC mínimo del 30%.
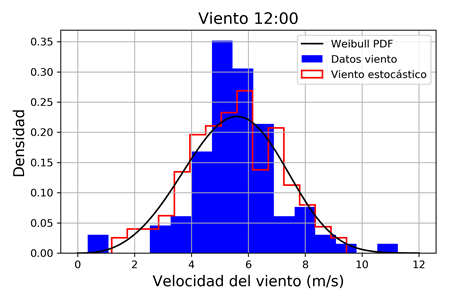
Primero se modelan las variables estocásticas de entrada (considerando que el BESS está desconectado) para cada hora del día. Para el caso de las variables climáticas, se han usado datos de velocidad de viento, irradiación solar y temperatura de Galápagos, obtenidos de [20], asumiendo que éstos le corresponden al área donde está instalada la microrred de prueba.
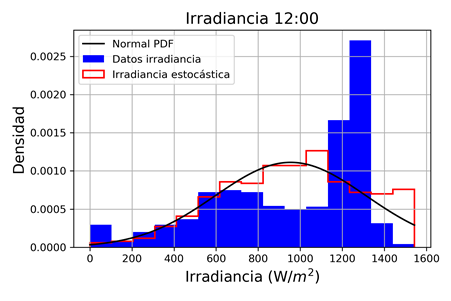
Las Fig. 4, 5 y 6 presentan los modelos estocásticos obtenidos para las 12:00. Para la velocidad del viento se ha usado la función de densidad de probabilidad (PDF) Weibull, en tanto que, para la irradiación solar y la temperatura, los datos se han ajustado a la PDF Normal.
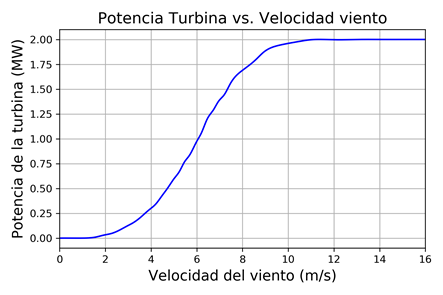
Para el caso del generador eólico, la velocidad del viento debe transformarse en potencia eléctrica, utilizando la curva “potencia vs. velocidad del viento”, la cual suele ser característica de los aerogeneradores. Para el caso del aerogenerador que forma parte de la microrred de prueba, se considera la curva presentada en la Fig. 7.
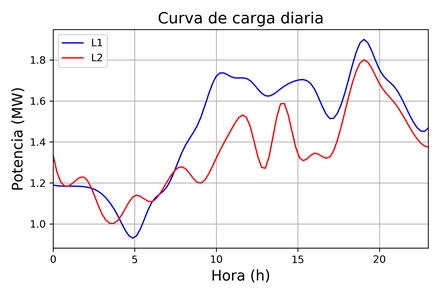
Para el generador PV se emplea la relación entre potencia generada, irradiación solar y temperatura presentada en [21]. Por otro lado, las cargas obedecen a una PDF Normal con desviación típica (() de 10% respecto de su valor esperado (medio µ). Se asume que el valor esperado de cada carga corresponde al dato del caso base para el sistema principal [19] y que para la microrred (L1 y L2) corresponde a los datos horarios que se presentan en la Fig. 8. La potencia reactiva se determina considerando que el factor de potencia puede ser representado por una PDF Normal con ( de 3%.
Usando estos datos se ejecutan simulaciones de Montecarlo para determinar los PPF horarios del sistema de prueba. Para esto, se parte de las siguientes consideraciones operativas: i) la microrred opera en modo “conectada a la red”, ii) el criterio de despacho de los generadores de la microrred está orientado a propender a un autoabastecimiento, considerando un despacho preferente de la energía renovable (esto hace que la microturbina sincrónica se despache en segunda prelación hasta que la demanda interna sea cubierta o hasta que se llegue al máximo de su capacidad), iii) en el caso que la microrred no sea capaz de autoabastecerse, se comprará energía de la red principal y en el caso que la microrred tenga exceso de generación renovable, ésta podrá ser vendida a la red externa, iv) los generadores de la red principal serán despachados considerando barras slack distribuidas, usando para el efecto el elemento “Power-Frequency Controller” *.ElmSecctrl disponible en PowerFactory.
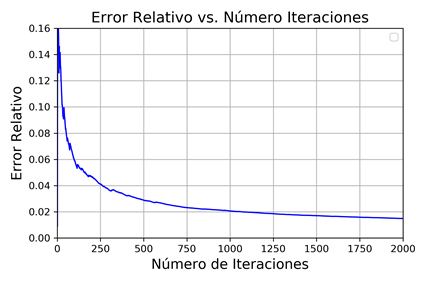
Antes de simular los PPF para cada una de las 24 horas del día, se realiza un análisis preliminar para determinar el número adecuado de iteraciones para cada Montecarlo. Para esto, se define como criterio de parada que el Error Relativo ((r) de la simulación de Montecarlo, para un nivel de confianza del 1%, sea menor al 2%. La Fig. 9 presenta la convergencia del Error Relativo de la “generación total renovable” (eólico más fotovoltaico) correspondiente a las 12:00 para diferente número de iteraciones. En esta figura, es posible apreciar que aproximadamente sobre las 1250 iteraciones se logra un error relativo menor al 2%. Por tanto, se escogen 2000 iteraciones para las simulaciones de Montecarlo de los 24 PPF.
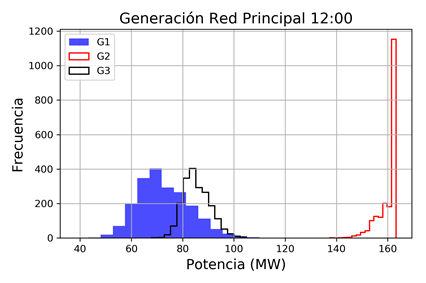
Las Fig. 10, 11 y 12 presentan histogramas de los resultados de la simulación de Montecarlo para las 12:00, correspondientes a la generación de potencia activa de la microrred, su voltaje en el punto de conexión principal (Barra PCC) y los resultados de la generación de la red principal, respectivamente.
A partir de los resultados para las 24 h del día, es posible analizar el comportamiento probabilístico de la generación fotovoltaica (PV). Con estos resultados probabilísticos (para 100 escenarios de probabilidad) se podrá definir el comportamiento de carga y descarga de una batería a instalarse junto con el generador fotovoltaico (PV-BESS) en cada escenario. Esta definición permitirá determinar el modelo estocástico del estado de carga del BESS para cada una de las 24 h. Para esto, se usan los valores de diseño del BESS (3.5 MW, 14 MWh) como referencias para el análisis de carga y descarga y se consideran las premisas operativas detalladas en el paso 7 de la sección 3.
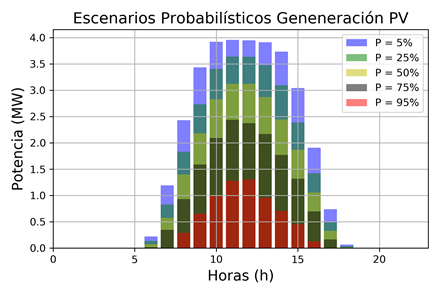
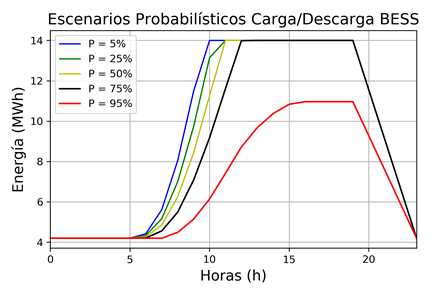
La Fig. 13 presenta 5 (de los 100) escenarios probabilísticos de generación del PV (para probabilidades del 5%, 25%, 50%, 75% y 95%), en donde es posible apreciar diferentes probabilidades de generación del PV, las cuales están asociadas a la carga de la batería. A partir de estos valores, y considerando las premisas operativas del sistema PV-BESS, es posible determinar 100 escenarios de estados probables de carga y descarga del BESS. La Fig. 14 muestra los 5 escenarios de estados de carga y descarga del BESS obtenidos para los mismos escenarios presentados en la Fig. 13.
Considerando que cada hora presenta 100 valores diferentes de estado de carga/descarga (asociados a cada uno de los escenarios probabilísticos definidos), es posible determinar una CDF de estado de carga (SOC) para cada hora (24 CDFs en total), los cuales se convierten en el modelo estocástico buscado. La Fig. 15 presenta los resultados de las CDFs del SOC del BESS para 5 horas diferentes: 7:00, 9:00, 12:00, 20:00 y 23:00.
Una vez definidas las CDF del SOC del BESS es posible realizar la simulación de Montecarlo para cada hora, considerando el sistema completo PV-BESS.
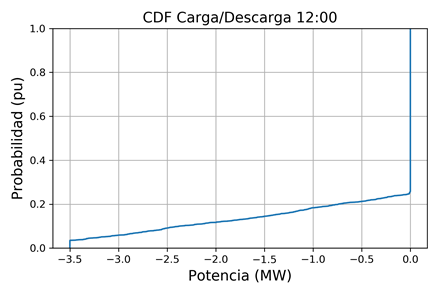
Las Fig. 16 y 17 presentan los resultados de la simulación de PPF para las 12:00, correspondientes a la generación de potencia activa de la microrred y la curva de distribución de probabilidad acumulada de carga y descarga del BESS. Es posible apreciar cómo la carga de batería (color magenta) modifica la generación de la microrred, causando un incremento en el despacho de la microturbina de gas (comparado con la Fig. 10), además que aparecen más escenarios en los que es necesario comprar energía desde la red principal.
Las Fig. 18 y 19 presentan los resultados de la simulación de PPF para las 20:00, correspondientes a la generación de potencia activa de la microrred y la curva de distribución de probabilidad acumulada de carga y descarga del BESS. En este caso, en cambio, es posible apreciar (color magenta) cómo la descarga de batería permite al sistema PV-BESS continuar abasteciendo de energía a la microrred, de acuerdo a la premisa operativa definida.
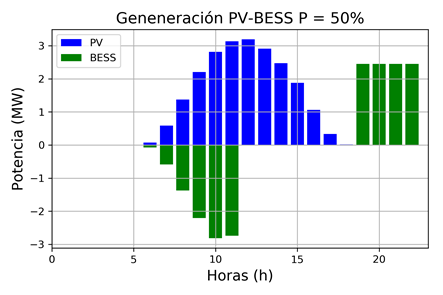
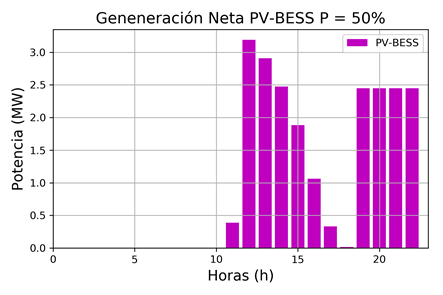
Finalmente, con el propósito de apreciar la operación del sistema PV-BESS (afectado por la carga y descarga de la batería), se realiza un análisis para un escenario probabilístico que representa el valor esperado (P=50%). Las Fig. 20 y 21 presentan los resultados de la operación del sistema PV-BESS, tanto en su operación independiente (generación del PV y carga/descarga del BESS), como en su producción neta (que es inyectada a la red), respectivamente.
CONCLUSIONES Y RECOMENDACIONES
Actualmente, los sistemas eléctricos de potencia están sujetos a varios desafíos operacionales que pueden satisfacerse mediante una efectiva integración y coordinación de microrredes, las cuales facilitan la explotación de los recursos renovables incluyendo alternativas de almacenamiento de energía (baterías).
Debido a la intermitencia del recurso primario de las energías renovables (irradiación solar, velocidad del viento, etc.) es necesario incluir en las metodologías de planificación los modelos estocásticos apropiados que simulen el comportamiento aleatorio de las variables. El comportamiento aleatorio del recurso renovable y de la demanda incide en el comportamiento estocástico de otros elementos de las microrredes, como es el estado de carga (SOC por sus siglas en inglés) de los sistemas de almacenamiento de energía a base de baterías (BESS). La estimación apropiada del SOC resulta de suma importancia en la planificación y gestión de baterías.
Este documento propone una novedosa metodología para la determinación del modelo estocástico del SOC basada en la probabilidad de carga y descarga de la batería, según el comportamiento de la generación PV. Para ello, se estructura un script en Python que permite evaluar, de forma probabilística, la operación de la microrred considerando la disponibilidad del recurso primario intermitente y la variabilidad de la demanda eléctrica. Como resultado, se determinan los modelos estocásticos del SOC del BESS para cada período de tiempo. La metodología propuesta a una microrred de prueba operando en modo “conectada a la red”, obteniéndose resultados prometedores. Posteriormente, estos modelos serán usados para definir un diseño óptimo del sistema PV-BESS de tal manera que se maximice el aprovechamiento del recurso primario.