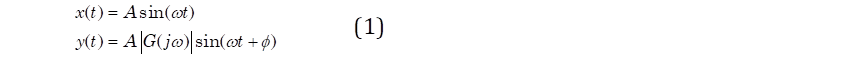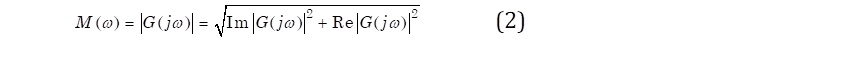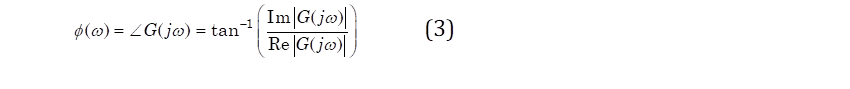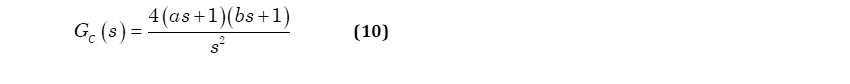Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El diseño de sistemas de control puede ser efectuado tanto en el dominio del tiempo como en el de frecuencia. La selección de uno u otro método generalmente se basa en las preferencias del diseñador, sin embargo, el método de análisis de la respuesta en frecuencia, además de aparentar ser el de mayor uso, tiene la ventaja de ayudar en gran medida a determinar las funciones de transferencia o en su defecto establecer el espacio de estados de un sistema a partir de mediciones o toma de datos en una planta [1], lo que en diversas ocasiones resulta crucial para el análisis del controlador [2].
Diversas aplicaciones basadas del análisis en el dominio frecuencial han sido planteadas en la literatura. En [3], se realiza un estudio numérico en el dominio frecuencial para problemas electromagnéticos basados en el cálculo exterior discreto. Incluso en diseño de filtros, como en [4], donde se propone un algoritmo para la selección automática del filtros que permitan suprimir el ruido generado naturalmente por trenes de pulsos. El análisis en el dominio frecuencial ha sido también aplicado en procesamiento de señales [5], [6], estudio de vibración de estructuras [7], respuestas sísmicas [8], medición de índices de refracción [9], espectroscopia [10], análisis de los sonidos producidos durante perforaciones [11], entre otros [12]-[14]. También, en el campo eléctrico se han desarrollado estudios encaminadas a la implementación de sistemas de conversión de energía mareomotriz usando una turbina regulada por pitch y un generador de inducción, el análisis en el dominio frecuencial en dicha investigación es empleada a la hora de considerar estrategias de control de velocidad que permitan operar al sistema al máximo de su potencia [15]. En [16], se presenta un método de análisis del acople rotor-estator para detección de campos inestables de flujo dentro de turbo máquinas mediante el método de dominio de frecuencial.
En el diseño de controladores se usan además representaciones gráficas tales como diagramas de Bode, diagramas de Nyquist o diagramas de Nichols, cuyo uso se justifica en la posibilidad de representar un amplio espectro de frecuencias en un solo gráfico, o la aparición de parámetros como margen de fase o margen de ganancia, mismos que resultan cruciales para la búsqueda de soluciones óptimas que lleven a los sistemas a la estabilidad o a su vez ayuden a sintonizar diferentes controladores [17], [18], [19] .
En el presente estudio se abarca el análisis de la respuesta en frecuencia empleando diagramas de Bode para su representación gráfica. En la sección II se presenta la formulación matemática ligada al análisis de la respuesta en frecuencia y los diagramas de bode, en la sección III se aborda el diseño de controladores mediante la respuesta en frecuencia incluyendo el concepto de criterios de margen de ganancia y margen de fase, con la intención de analizar la importancia de estos en cuanto a evaluar la estabilidad de un sistema y con ello identificar los posibles escenarios y estrategias a llevarse a cabo para de ser el caso, llevar al sistema a la estabilidad, finalmente en la sección IV se plantean las conclusiones sobre el estudio realizado.
FORMULACIÓN MATEMÁTICA
Dada una función de entrada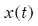 
de carácter sinusoidal, la salida de dicha señal 
vendrá dada por (1).
Para realizar el análisis frecuencial es importante recabar varios aspectos de importancia en el dominio frecuencial tales como magnitud (2) y fase (3).
De cara a la implementación de diagramas de bode, también es necesario conocer la expresión que permite transformar una magnitud a decibelios (4).
DISEÑO MEDIANTE RESPUESTA EN FRECUENCIA
La ventaja del diseño de controladores en el dominio frecuencial se debe a que los factores producto y cociente de las funciones de transferencia se convierten en sumas o restas [18].
De la mano al análisis frecuencial, se emplean herramientas gráficas, siendo la de mayor los diagramas de Bode, que permiten representar la respuesta de un sistema en dos gráficas. Un diagrama de magnitud en donde se grafica la relación de amplitud en decibelios contra el logaritmo de la frecuencia. El valor de amplitud expresado en decibelios se obtiene mediante la expresión (4) citada anteriormente. El diagrama de fase por su parte, presenta una gráfica del ángulo de fase de la función de transferencia contra el logaritmo de la frecuencia [17], [18].
El análisis del margen de ganancia y margen de fase para el diseño de controladores supone una estrategia interesante e información crucial sobre las posibles medidas que se pueden tomar frente a la aparición de respuestas inestables, esto ya que son medidas de estabilidad relativa. Así pues, todo sistema es estable cuando cumple con el criterio (5).
Los conceptos de margen de ganancia y fase no solo indican la estabilidad en términos absolutos, también permiten dar un margen sobre qué tan lejos está en sistema de la estabilidad o inestabilidad, esto ya que mientras más pequeños se hagan los valores del margen de ganancia y de fase más tenderá el sistema hacia la inestabilidad y viceversa [18].
Casos de Estudio
A continuación, se proponen varias funciones de transferencia en las que se determinará el margen de ganancia y fase para posteriormente corroborar el comportamiento del sistema de forma que sea posible definir si el mismo es estable o inestable. De ser inestables se aplicarán diversos controladores hasta llegar a la estabilidad.
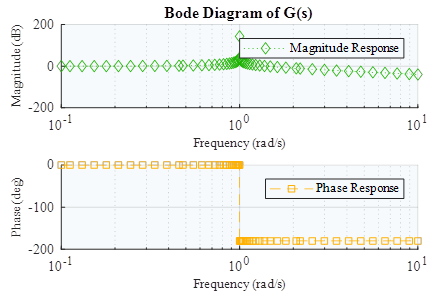
Dada la función de transferencia (6), se obtiene el diagrama de Bode mostrado en la figura 2.
La respuesta en magnitud del sistema para una frecuencia unitaria tiene a infinito, mientras que la respuesta en fase para la misma frecuencia cambia de 0 a -180 grados de forma abrupta.
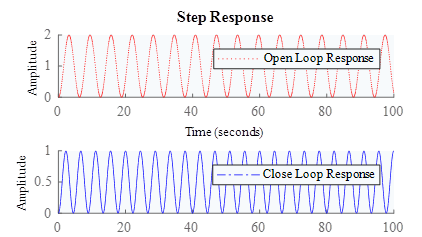
Al dotar al sistema de una entrada del tipo escalón unitario, se obtiene la respuesta mostrada en la figura 3. Dicha gráfica presenta dos señales correspondientes a la respuesta en lazo abierto y lazo cerrado. Para la respuesta en lazo abierto simplemente se incluyó a la planta la entrada escalón y como resultado se obtiene una señal no amortiguada, haciendo el sistema inestable, dicha señal posee un valor pico de dos. En cambio, para la respuesta en lazo cerrado, se realizó una realimentación unitaria a la planta obteniendo una señal no amortiguada que provoca que de igual forma el sistema sea inestable, a diferencia de la respuesta en lazo abierto, la amplitud de la respuesta de lazo cerrado es unitaria y la señal periódica tiene una mayor frecuencia de oscilación.
Con la intención de llevar al sistema más cerca de la estabilidad, se coloca en serie un controlador proporcional integral cuya función de transferencia responde a (7).
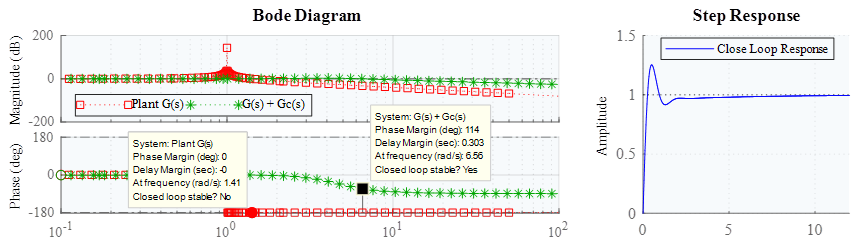
En la figura 4 se puede apreciar el diagrama de bode para la planta el controlador y la implementación del controlador en serie a la planta. Para cada uno de ellos se especifica su margen de fase obteniendo como resultado que solamente el controlador presenta una respuesta estable. De esta forma, aún después de haber incluido el controlador a la planta la totalidad del sistema sigue siendo inestable, por lo que se debe considerar otro tipo de control que acerque aún más al sistema a la estabilidad.
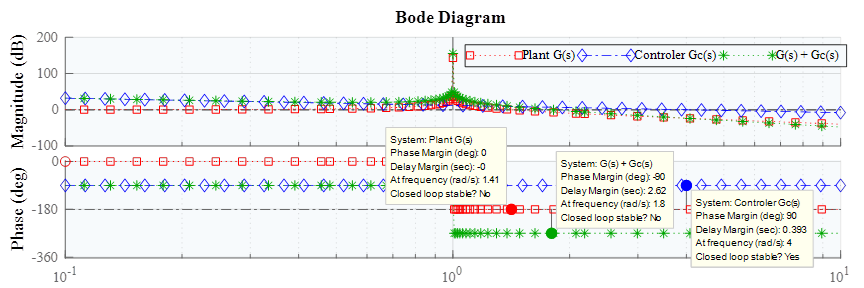
Figura 4: Diagrama de Bode de la planta G(s), controlador proporcional integral Gc(s) y Gc(s) + G(s)
El controlador proporcional integral causa una atenuación y el desplazamiento de la respuesta en fase de -90 grados. La ganancia contenida en el controlador contribuye con una amplificación de 12.04 decibelios y el integrados con una atenuación de 20 decibelios por década. Estas implicaciones ligadas al controlador influyen directamente a la planta provocando un cambio en su respuesta en magnitud y fase.
Para corroborar la inestabilidad del sistema se implemente nuevamente una realimentación unitaria al mismo y como entrada se incluye una señal escalón unitario, el resultado obtenido se presenta en la figura 5.
Como se puede apreciar la salida del sistema aproximadamente a los noventa segundos converge, lo que indica que efectivamente el sistema es inestable, sin embargo, en contraste a la respuesta inicial, en la que no se incluía ningún tipo de control esta respuesta no posee el comportamiento no amortiguado y parte de la estabilidad.
El nuevo controlador por considerar será del tipo proporcional, integrativo y derivativo (PID) con función de transferencia (8).
Los valores calculados para que el sistema en lazo cerrado no salga de control se establecen los valores para a y b son 5 y 0.25 respectivamente. El diagrama de bode de la planta, el nuevo controlador y la inclusión del controlador en serie a la planta se presenta en la figura 6.
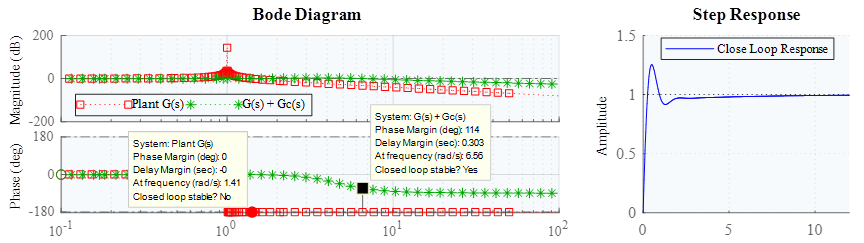
Figura 6: Diagrama de Bode de la planta y el sistema con controlador PID con la respuesta debido a una entrada escalón en lazo cerrado.
Con la inclusión del controlador PID se lograr que el sistema sea estable, como se puede apreciar en la figura, el margen de fase ahora se ubica en 114 grados, y al ser mayor a cero implica que el sistema alcanzó la estabilidad.
Al efectuar una realimentación unitaria del sistema y dotarlo de una entrada escalón unitario se obtiene la respuesta también mostrada en la figura 5. La señal obtenida presenta un comportamiento estable fijándose en uno luego de experimentar un pico en su amplitud.
El valor a contribuye con hasta noventa grados de adelanto de fase en la región de altas frecuencias. Mientras que el valor de b proporciona un margen de fase de al menos cincuenta grados y un margen de ganancia infinito. En conjunto los datos ligados al controlador hacen que el sistema diseñado satisfaga los criterios de estabilidad haciendo que el sistema adquiera un comportamiento aceptable.
El análisis del lugar de las raíces del sistema también puede suponer un método satisfactorio que permita comprobar la estabilidad de la planta al haber sido incluido un controlador en serie a la misma. En la figura 7 se muestra el diagrama de polos y ceros del sistema, en la misma se puede apreciar que los polos se ubican a la izquierda del eje imaginario, dos de los polos son complejos conjugados y uno real, por otra parte, los ceros ad- quieren valores reales negativos y también se ubican a la izquierda del eje imaginario.
En la figura 8 se muestra el diagrama de Bode de la función de transferencia de la planta en serie al controlador en lazo abierto. Como se puede apreciar el margen de fase se ubica en 55 grados, al ser positiva el sistema es estable aun en lazo abierto.
Ahora, se propone centrar el análisis de sistemas de control al aplicarlos a un generador eléctrico síncrono, cuya función de transferencia está definida por (9); el modelo se obtuvo a través del método de identificación dinámico por medio del test escalón, que busca, frente a variaciones abruptas en la magnitud del escalón, reconocer variaciones de la tensión en el generador.
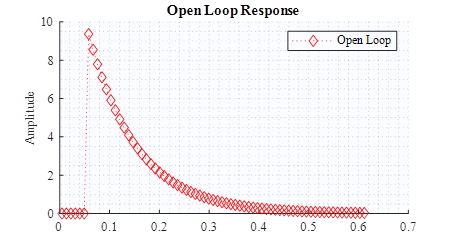
Además de lo anterior es importante considerar que la planta sin consideraciones adicionales se comporta de forma inestable, esto se puede observar en la figura 10, que muestra la respuesta en lazo abierto del sistema.
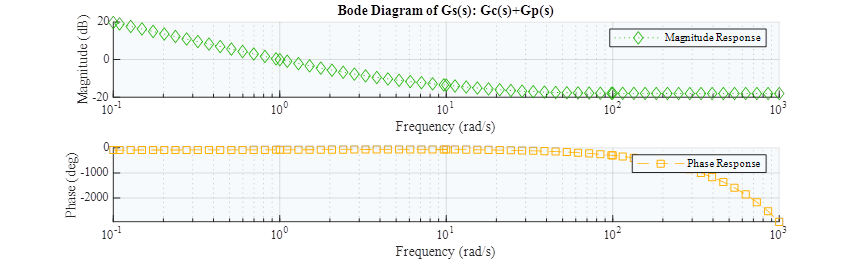
El diagrama de bode de la función de transferencia que representa la implementación del controlador acoplado al generador se puede observar en la figura 10. La respuesta en magnitud experimenta una variación constante de diez decibelios por década, en frecuencias menores a diez; para frecuencias mayores la magnitud permanece constante fijándose en cincuenta decibelios. En la respuesta en fase, para frecuencias menores a cien rad/segundo el ángulo se mantiene en cero, mientras que frecuencias mayores provocan un decremento progresivo del ángulo a medida que aumenta la frecuencia tendiendo a menos infinito.
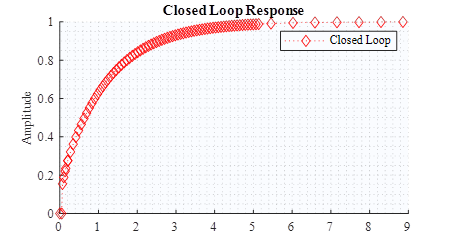
El controlador propuesto consta de dos ceros y dos polos ubicados en el origen, tal y como se aprecia en la ecuación (10). En cuanto a valores de las constantes a y b se consideraron como 0.05 y 0.25 respectivamente, logrando en conjunto a todo el controlador, alcanzar la compensación del sistema y con ello su estabilidad. Los valores empleados, se obtuvieron a través de pruebas iterativas en las que se verifico de forma continua la estabilidad o inestabilidad del sistema. El resultado de aplicar el controlador a la planta arroja la respuesta mostrada en la figura 11, con sistema en lazo cerrado.
La inserción de procedimientos de control al sistema eléctrico de potencia se sustenta en la necesidad de garantizar la estabilidad del sistema eléctrico, por lo que es indispensable establecer estrategias de control que permitan encontrar los parámetros idóneos con los que se asegure un correcto funcionamiento de generadores, logrando con ello preservar la estabilidad del sistema.
Los problemas de estabilidad en sistemas eléctricos de potencia pueden darse por ángulo o tensión, y se estudian considerando la capacidad de las máquinas de recobrar el sincronismo tras perturbaciones como variaciones en la demanda de potencia. Allí, los sistemas de control cumplen un rol esencial, pues evitan que las máquinas en un momento dado operen en regímenes inestables y atenten contra el resto del sistema eléctrico. De ahí que se requiera el estudio de mecanismos de control como el aplicado en el presente estudio sobre el generador, pues sirven de punto de partida para identificar aquellos controladores que pueden presentar una solución interesante antes los problemas que generan inestabilidad en un sistema eléctrico, y no solo eso, también se pueden incluir controladores a la hora de buscar garantizar aspectos como una correcta sincronización de un generador a la red, control sobre temperatura o vibración, que permitan efectuar un mantenimiento oportuno sobre los equipos, entre otros.
CONCLUSIONES Y RECOMENDACIONES
El diseño de sistemas de control basados en la respuesta en frecuencia supone la ventaja de permitir predecir él comportamiento de un sistema al incluir un controlador, ya que juntamente con las herramientas gráficas tanto la respuesta en frecuencia de la planta y el controlador pueden ser sumadas permitiendo de forma clara implementar mecanismos de control para garantizar la estabilidad del sistema.
La respuesta en frecuencia de un sistema presenta ventajas interesantes puesto que se basa en el análisis del comportamiento de cualquier señal periódica, de forma que, para calcular la salida de un sistema lineal ante cualquier señal periódica, sólo es necesario conocer la respuesta de este ante un conjunto de señales sinusoidales de frecuencias múltiplos de la señal original.
Los criterios de margen de ganancia y fase representan un criterio útil y apropiado para determinar la estabilidad de un sistema, para los casos propuestos se pudo verificar como este concepto era válido ya que a medida que el sistema propuesto por acción de controladores se acerca al margen de ganancia, la respuesta va tendiendo a la inestabilidad.
La metodología propuesta se aplicará a trabajos futuros en el control, operación en sistemas eléctricos de potencia y control de convertidores de potencia destinados a generadores distribuidos utilizando energía renovable.
Se plantea como trabajos futuros experimentos de identificación de algunas máquinas eléctricas en el tiempo continuo y discreto. Aplicar el controlador diseñado en un sistema real y presentar los resultados alcanzados. Implementar el control en un sistema en tiempo real, con esto verificar el funcionamiento del procedimiento de diseño planteado.
