Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
En la actualidad, el factor de rendimiento teórico de un parque eólico es de suma importancia para impulsar la construcción de nuevos proyectos que aprovechen este tipo de recurso. Según Hernández-Escobedo et al, el análisis del potencial eólico con fines de generación eléctrica incluye: la selección de la potencia del aerogenerador a instalar, los datos de velocidad de viento y las estimaciones de la densidad del aire, la misma que depende de variables como la presión atmosférica y la temperatura [1].
La presión atmosférica se define como la presión ejercida por la atmosfera en un punto o unidad de área. Al medir la presión a nivel del mar con una temperatura ambiente de 20 (°C) y una densidad de aire de 1.22 (kg/m3), se obtiene un valor aproximado a 1010 (hPa) [2].
Debido a que la densidad del aire disminuye a medida que la altura (con relación al nivel del mar) de un emplazamiento aumenta se espera que la presión también varié. En este contexto, cabe mencionar que para realizar estudios de potencial eólico en una zona se debe considerar que no todos los posibles emplazamientos se encuentran a nivel del mar, por lo que es fundamental el cálculo de la presión en cada lugar, misma que disminuye de forma logarítmica al aumentar la altitud. En el desarrollo de este cálculo se toma en cuenta la relación de la presión con la altura, la ley del gas ideal y la energía potencial gravitacional [3-5].
Por otro lado, existe una diversidad de estudios para la caracterización de las curvas de potencia de las turbinas, las cuales se encuentran citadas en la bibliografía. Estas curvas permiten caracterizar la producción de energía de la turbina, dependen de la velocidad del viento, y esta a su vez se ve influenciada por la densidad de aire [6-12].
En este trabajo, se ajustó la función sigmoide para la curva de potencia de un aerogenerador de 2 MW [13-17] y se la interpoló con el mapa de densidad de aire junto con los mapas de velocidad de viento, altura y presión atmosférica para obtener el mapa de potencial eléctrico del Ecuador dadas las condiciones propias de cada zona del país. Se construyó la curva de potencia teórica para los datos de velocidad del viento y potencia para el aerogenerador, y de esta forma, se construyeron las bases para realizar las simulaciones en dinámica de fluidos con WindSim [18].
METODOLOGÍA
El desarrollo del presente artículo se basa en dos etapas, la primera que consiste en a) la recopilación de información; y la segunda en b) el cálculo del potencial eolo-eléctrico.
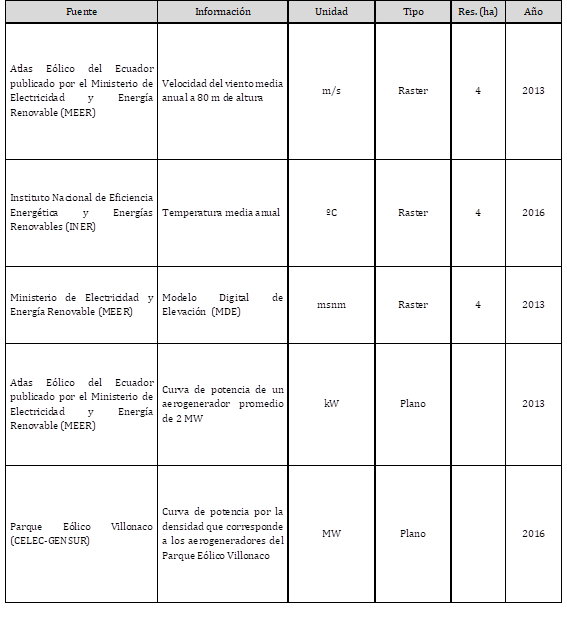
Recopilación de información: La información recolectada es procedente de fuentes oficiales gubernamentales y se encuentra en formatos planos y espaciales que permiten su interoperabilidad y procesamiento conjunto. En el caso de información espacial, su resolución es de 200 x 200 (m). En la Tabla 1, se observa las fuentes de datos y el tipo de información recolectada.
En cuanto a la velocidad del viento anual simulada a 80 metros de altura sobre el suelo, las velocidades medias más altas se encuentran en la cordillera y muchas zonas superan los 11 (m/s). Mientras, que la región costa y oriente tienen velocidades medias cercanas a los 6 (m/s) en los mejores casos. Por otro lado, la cobertura de temperatura media anual proveniente del INER, se obtuvo a partir de datos meteorológicos medios mensuales de estaciones administradas por el Instituto Nacional de Meteorología e Hidrología (INAMHI).
Finalmente, se utilizaron los datos de una curva de potencia de un aerogenerador promedio de 2 (MW) para la estimación del potencial eléctrico. Estos datos corresponden a los propuestos en el Atlas Eólico del Ecuador y se encuentran en la Tabla 2.
Tabla 2: Valores de la curva de potencia para un aerogenerador promedio de 2 (MW) para una densidad del aire de 1.225 (kg/m3).
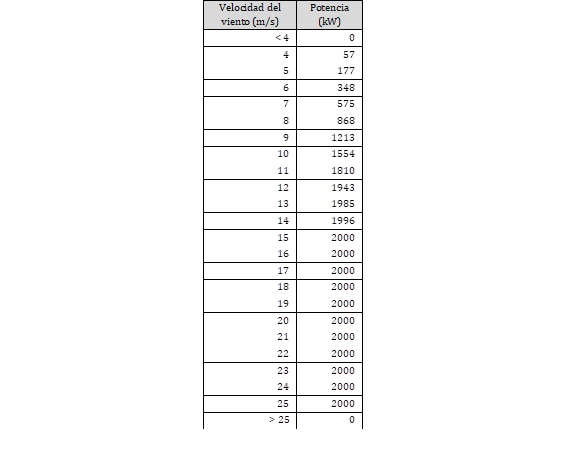
Los datos utilizados para aproximar la corrección de la curva de potencia por la densidad corresponden a los aerogeneradores del Parque Eólico Villonaco, los cuales fueron provistos por la Corporación Eléctrica del Ecuador - GENSUR [19]. La curva de potencia de los aerogeneradores de Villonaco a nivel del mar comparado con la curva a una densidad de 0.89 (kg/m3) se presenta en la Fig. 1.
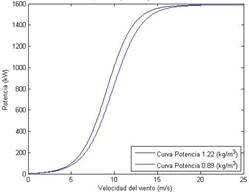
Figura 1: Curva de potencia para aerogeneradores de 2 (MW) para las densidades del aire a 1.225 (kg/m3) y 0.89 (kg/m3).
Cálculo del potencial Eolo-eléctrico
La determinación del potencial eléctrico basado en un aerogenerador promedio de 2 (MW), se lo realizó aproximando la curva de potencia de la Tabla 2 a una función continua; se hallaron los mapas de presión atmosférica y densidad del aire; y se estimaron los valores de potencia media a los que los aerogeneradores promedio estarían funcionando en base a las velocidades del viento media anual a 80 metros sobre el suelo.
Se tomó una sigmoide para ajustar la curva de potencia del aerogenerador con los datos de la Tabla 2, la cual se encuentra expresada en la Ecuación (1).
Donde,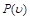 
es la potencia sigmoidal aproximada a la curva de potencia, 
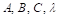y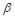 
son las constantes de la interpolación no lineal, y 
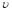es la velocidad del viento observada para una resolución temporal de 10 minutos. La primera derivada de la Ecuación (1) se demuestra a continuación.
En base a la Ecuación (2) se encuentra el punto de inflexión de la curva derivando una vez más para la variable de velocidad del viento, e igualando a cero toda la expresión, Ver Ecuación (3).
La constante de decaimiento de la exponencial de la Ecuación (1) varía en relación a las densidades que se desea calcular, como se demuestra en la Ecuación (4). Esto se estimó a partir de la corrección de la potencia para diferentes densidades de aire, como recomienda la norma ISO 2533:1975 y los datos de las curvas de potencia de los aerogeneradores de Villonaco [21].
La corrección de densidad del aire para los aerogeneradores de Villonaco se realizó a partir de la aproximación de la Ecuación (1) para las dos densidades de la Figura 1. Por tanto, la constante de decaimiento exponencial es la única que cambia, obteniendo una relación lineal para aproximar las constantes en función de la densidad del aire.
Donde,
En la Ecuación (5), se demuestra la relación lineal que se obtuvo de la variación de las constantes de decaimiento de la exponencial interna de la sigmoide.
Como se especificó en la Tabla 2, los datos de la curva de potencia corresponden a la densidad del aire a nivel del mar y condiciones estándar. Así, la Ecuación (1) estaría expresada de la siguiente manera.
Donde,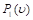 
es la potencia corregida para una densidad del aire menor a la estimada a nivel del mar. Para la estimación del mapa de densidad se determinó la presión atmosférica en función de la relación barométrica que existe entre la altitud y la presión [22]. Relación expresada en la Ecuación (5).
Donde,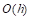 
es la presión atmosférica a una altura sobre el nivel del mar, 
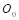es la presión atmosférica a nivel del mar, la cual se aproxima a 1010 (mb), 
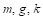son constantes correspondientes a la masa molar del aire, gravedad y Boltzmann, respectivamente. Por último, 
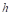y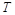 
son la altura correspondiente al mapa de elevación del modelo digital de elevación y la temperatura media anual.
La densidad del aire es estimada a partir de la relación de los gases ideales, así como lo recomienda la ISO 2533:1975. La densidad del aire se encuentra expresada en la Ecuación (8).
Donde,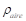 
es la densidad del aire, 
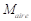es la masa molar del aire igual a 0,028963512440 (kg/mol), 
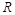es la constante universal de los gases igual a 8.314472 (Pa*m3/mol*K), 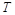es la temperatura y 
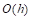es la presión atmosférica. Reemplazando la Ecuación (7) en la Ecuación (8) se obtiene la densidad del aire en relación a la altitud y la temperatura, la cual se muestra en la ecuación (9).
RESULTADOS
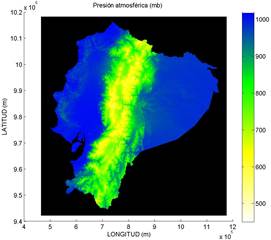
Como uno de los resultados se obtuvo el mapa de presión atmosférica. Se puede apreciar que la presión atmosférica en la cordillera es baja y puede llegar a valores de hasta 500 (mb). La presión a nivel del mar es aproximada a los 1010 (mb) en condiciones estándar. Por otro lado, la región oriente puede tener valores sobre los 900 (mb), ver Fig. 2.
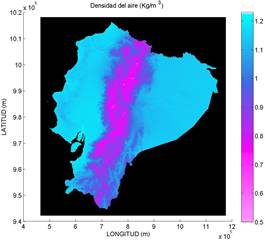
En base al mapa de presión atmosférica determinado para el Ecuador continental y según la cobertura de temperatura media anual se pudo obtener la densidad de aire, que se encuentra simplificada según la Ecuación (8). En la Fig. 3 se observa este resultado mapeado. Donde, la densidad del aire para la región costa se aproxima a 1.225 (kg/m3), en el oriente pueden llegar a 1 (kg/m3) y en la región de la cordillera pueden tener valores hasta 0.7 (kg/m3).
La curva de potencia para un aerogenerador promedio de 2 (MW) y densidad del aire de 1.225 (kg/m3) fue ajustada a la sigmoide de la Ecuación (1), la cual se expresa a continuación.
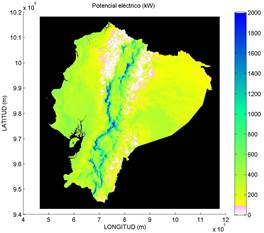
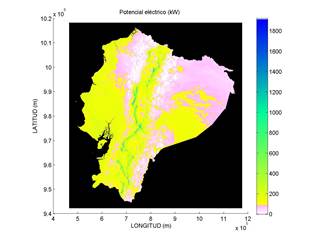
En base a la interpolación para la curva de potencia de 2 (MW) para una densidad del aire de 1.22 (kg/m3), se estimó el potencial eléctrico, que corresponde a la potencia media aproximada con la que el aerogenerador funcionaría anualmente para cada pixel del mapa de velocidad del viento del Ecuador, a 80 metros sobre el suelo. En la Fig. 4, se presenta el mapa de potencial eolo-eléctrico para el Ecuador en base al aerogenerador promedio de 2 (MW).
Por otro lado, la corrección de densidad se realizó en base a la Ecuación (4), y se pudo aproximar las curvas de potencia para densidades del aire inferiores a la del nivel del mar o 1.22 (kg/m3). En la Fig. 5, se comparan dos curvas de potencia para dos diferentes densidades de aire, las cuales toman valores característicos al comportamiento de la sigmoide.
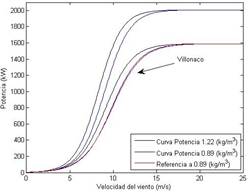
Figura 5: Curva de potencia referencial a una densidad del aire de 1.22 (kg/m3), comparada a una curva de 0.89 (kg/m3).
En la Figura 5, es posible apreciar el cambio en el comportamiento de la curva de potencia para la densidad del aire a 0.89 (kg/m3), esto se debe al factor exponencial en la ecuación de la sigmoide, el cual cambia la constante de decaimiento en relación a ambas densidades, como fue demostrado en la metodología. La curva de potencia de color azul corresponde a la aproximación obtenida a partir de la Ecuación (6), la cual presenta un error pequeño en el ajuste a los aerogeneradores de Villonaco. El coeficiente cuadrado de correlación entre la curva de potencia de los aerogeneradores de Villonaco y la aproximación es de 0.99 y el error medio es de 5.61 (kW).
En la Fig. 6, se observa el mapa de potencial eléctrico del Ecuador, el cual entrega información cada una de las regiones, donde la densidad del aire constante corresponde a los valores cercanos a 1.225 (kg/m3) o máximos.
Finalmente, las correcciones de densidad del aire para el potencial eléctrico de todo el Ecuador, en base a las Ecuaciones (4) y (6) de la sección de Metodología, dan como resultado la Figura 6, donde los valores del potencial eléctrico para el Ecuador se encuentran en el rango de los 200 a los 1200 (kW). Además, este mapa entrega información de lugares donde se puede construir un emplazamiento eólico en un área de 200 x 200 (m), considerando que en estas áreas se puede instalar un aerogenerador de 2 (MW). Se puede estimar un factor de rendimiento del aerogenerador en estudio dividiendo la potencia estimada para la potencia nominal, el cual deberá ser validado con el factor estimado a partir de torres de medición en la zona.
CONCLUSIONES
Todos los datos de la curva de potencia correspondiente a un aerogenerador de 2 (MW), se acoplaron a una función sigmoide que permitió calcular la potencia aproximada de un emplazamiento en base a la velocidad del viento para una resolución temporal de 10 minutos.
Debido a que la densidad del aire en todo el Ecuador no es la estimada a nivel del mar, la corrección de la curva de potencia con la densidad del aire para cada zona del país en base a las recomendaciones de la norma IEC 61400-1 y los datos de los aerogeneradores de Villonaco (Curvas corregidas a una densidad de 0.89 kg/m3), fue de vital importancia para asemejar las condiciones operacionales de las turbinas en cada emplazamiento del país. El error medio que se obtuvo en la comparación de ambas curvas de potencia es de 5.61 (kW), el cual es bajo y no representa pérdidas sobre los 5 (m/s).
Para realizar el cálculo del potencial eléctrico de una zona a condiciones reales y no ideales es indispensable relacionar tres aspectos importantes: la relación barométrica entre la altitud y la presión, la altitud y la densidad del aire, la temperatura y velocidad del viento.
Estas variables se ven claramente reflejadas en el mapa de potencial eléctrico obtenido de este estudio, el cual permitirá estimar las zonas con mayor potencial eólico para su aprovechamiento y contribución al cambio de la matriz energética.
El mapa de potencial Eolo-Eléctrico entrega información de la potencia media con la que un aerogenerador de 2 (MW) trabajaría en una zona de interés en una resolución de 200 metros. El factor de rendimiento se aproxima al de planta del aerogenerador en funcionamiento, esto debe ser validado en estudios de prefactibilidad con torres de medición siguiendo la norma IEC 61400-1.
