INTRODUCCIÓN

La comprensión lectora, proceso fundamental del aprendizaje, permite comprender e interpretar lo que se lee. Para ^{Molina (2020}) resulta la capacidad de interpretar el significado de un texto. Esta habilidad implica no solo reconocer las palabras, sino relacionar ideas y conceptos para sintetizar la información. Es crucial que los estudiantes desarrollen esta habilidad para poder extraer y construir el significado de los textos, lo que requiere buenos hábitos de lectura y actividades que fortalezcan el análisis crítico.

En el contexto de las matemáticas, la comprensión lectora juega un papel crucial, debido a que los estudiantes deben ser capaces de decodificar y entender los enunciados de los ejercicios para resolverlos de manera efectiva, “

En América Latina y el Caribe han experimentado un índice pronunciado referente a los niños de educación primaria que no pueden comprender un texto simple

” (^{Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura [UNESCO], 2023, p. 45}). A menudo los estudiantes enfrentan dificultades, no por carecer de habilidades numéricas, sino por no poder codificar el lenguaje utilizados en los problemas.

Las matemáticas es una de las áreas esenciales dentro del aprendizaje, porque otras ciencias como biología, química, física o economía dependen de ellas. Según ^{Gómez y Reyes (2022}) las matemáticas son una ciencia exacta que puede aplicarse en diversas situaciones cotidianas. El currículo en esta asignatura busca desarrollar habilidades de pensamiento lógico y crítico que permitan a los estudiantes interpretar y resolver problemas relacionados con su vida diaria.

La educación en América Latina enfrenta retos debido al bajo rendimiento de los estudiantes. La ^{UNESCO (2024)} manifiesta que “América Latina y el Caribe están por debajo del ranking global porque tiene puntales inferiores en las tres evaluaciones: Matemáticas, Lectura y Ciencias, esto significa que no alcanzan las competencias básicas” (p. 23). Existe una alta inequidad en el aprendizaje, en consecuencia, muchos estudiantes tienden a un desempeño deficiente.

La comprensión lectora en matemáticas facilita a los estudiantes comprender, analizar y resolver los problemas planteados en los textos. ^{Benavides y Zambrano (2023}) destacan que esta habilidad permite entender y procesar la información de los enunciados. Por lo tanto, fortalecer la lectura, mejora el análisis reflexivo y, a su vez, el rendimiento académico en esta asignatura.

Las pruebas del Regional Comparativo y Explicativo (ERCE) son de gran relevancia, porque evalúan el conocimiento de los estudiantes en diversas asignaturas. Según la ^{UNESCO (2022)}:

Ecuador ha sido partícipe en las pruebas del Regional Comparativo y Explicativo (ERCE), el séptimo grado de Educación General Básica obtuvo un total de 684 puntos de 1000 puntos, y se encuentra muy por debajo del promedio regional de 689 puntos. (p. 56)

Estos datos confirman que el conocimiento y el rendimiento académico de los estudiantes se encuentran asociados con la comprensión lectora.

Los problemas matemáticos requieren que el estudiante lea y comprenda el enunciado antes de resolverlo. Si no cuenta con habilidades de lectura y comprensión para identificar las palabras clave, no podrá resolver el ejercicio propuesto. Por ende, el objetivo de la investigación realizada fue determinar la relación entre la comprensión lectora y el aprendizaje de las matemáticas. Para abordar esta problemática, se plantearon las siguientes hipótesis:

H₀: No existe correlación entre la comprensión lectora y el aprendizaje de las matemáticas.

H₁: Existe correlación entre la comprensión lectora y el aprendizaje de las matemáticas.

METODOLOGÍA

El presente artículo de investigación se desarrolló bajo un enfoque cuantitativo de tipo descriptivo y correlacional, sustentado en una investigación de campo. Este diseño metodológico se fundamenta en los postulados de ^{Muñoz y Solís (2021}), quienes destacan que el enfoque cuantitativo es ideal para medir variables, analizar datos numéricos y establecer relaciones entre fenómenos.

La elección del diseño descriptivo se basa en ^{Ramos (2020}), quien señala que el diseño descriptivo permite identificar y caracterizar aspectos relevantes de una población. Asimismo, el diseño correlacional sigue los lineamientos planteados por este autor, en cuanto a establecer relaciones entre dos variables de interés.

Para el desarrollo de la investigación se ejecutaron 6 pasos:

La población estuvo constituida por 38 estudiantes del subnivel superior de Educación General Básica (EGB) (octavo, noveno y décimo) de la Escuela Océano Pacífico. Se empleó un muestreo no probabilístico por conveniencia, fundamentado en la facilidad de acceso y participación voluntaria de los estudiantes, además, el subnivel superior comprendido entre octavo y décimo es una etapa en la que se consolidan los conocimientos y se fortalecen las capacidades cognitivas.

Según ^{Hernández (2021}) el muestreo no probabilístico por conveniencia permite al investigador seleccionar a los participantes que formaran parte del estudio según criterios específicos preestablecidos. En la investigación ejecutada, estos criterios se relacionaron con la accesibilidad, disponibilidad o disposición de los individuos para participar, garantizando que la selección respondiera a las necesidades del estudio y mantuviera rigor científico, credibilidad y calidad de los resultados.

Por lo tanto, la muestra estuvo compuesta por 20 estudiantes del noveno grado de EGB pertenecientes al subnivel superior de la institución mencionada. Este hecho se atribuye a la accesibilidad directa a los estudiantes y características que permiten abordar la relación entre la comprensión lectora y el aprendizaje de las matemáticas.

Sin embargo, el estudio presentó limitaciones relacionados con el tamaño de la muestra, su alcance y diversidad tanto en términos de ubicación geográfica como de características socioeconómicas que limita la generalización de los resultados a otros contextos o niveles educativos. Además, el uso de un muestreo no probabilístico por conveniencia, aunque práctico, puede inducir sesgos al seleccionar participantes según su accesibilidad y disponibilidad, en lugar de su representatividad.

En cuarto lugar, se aplicó dos instrumentos para la recolección de datos (test de conocimientos y un cuestionario).

En primera instancia se aplicó un test de conocimientos adaptado del banco de datos del Libro de noveno grado de Educación General Básica, unidad 3 del bloque curricular de álgebra y funciones, constó de un total de 12 reactivos con respuestas de selección múltiple. Seguidamente, se empleó un cuestionario adaptado a una escala de Likert del 1 al 4 para el análisis de resultados, para determinar el nivel de comprensión lectora de los estudiantes.

El contenido de los dos instrumentos fue sometido a evaluación por un profesional docente de la Universidad Técnica de Cotopaxi y dos profesionales docentes de la Escuela Océano Pacífico con una larga trayectoria laboral. Tras la revisión, se realizaron ajustes en la redacción y estructura de los ítems para garantizar su claridad y pertinencia; se obtuvo una fiabilidad Alpha de Cronbach de 0,846.

Además, se solicitó el consentimiento informado de los participantes, con el propósito de garantizar el respeto a los principios éticos relacionados con la confidencialidad, el anonimato y el uso responsable de la información proporcionada. Se elaboró un documento de consentimiento informado, el cual incluyó una explicación clara y comprensible del propósito del estudio, la descripción de las actividades que los participantes deberían realizar (test de conocimientos y un cuestionario), la garantía de que la participación era completamente voluntaria y que los participantes podían retirarse en cualquier momento sin preocupaciones; la declaración de confidencialidad donde se aseguraba que los datos recopilados serían utilizados únicamente con fines académicos y tratados de manera anónima para proteger la identidad de los participantes.

El consentimiento informado fue firmado por los representantes legales de los estudiantes y, en caso de los participantes, se incluyó una sección en la que manifestaron su conformidad para participar en la investigación.

En quinto lugar, procesamiento y análisis de la información obtenida con el software estadístico SPSS.

Para el análisis e interpretación de los datos recopilados se utilizó el software estadístico SPSS v25, herramienta estadística que facilitó el procesamiento, análisis y representación de los datos obtenidos.

En sexto lugar, y como colofón del proceso investigativo, se procedió a la elaboración de conclusiones, con evaluación de la influencia de la comprensión lectora en el proceso de aprendizaje de las matemáticas.

RESULTADOS Y DISCUSIÓN

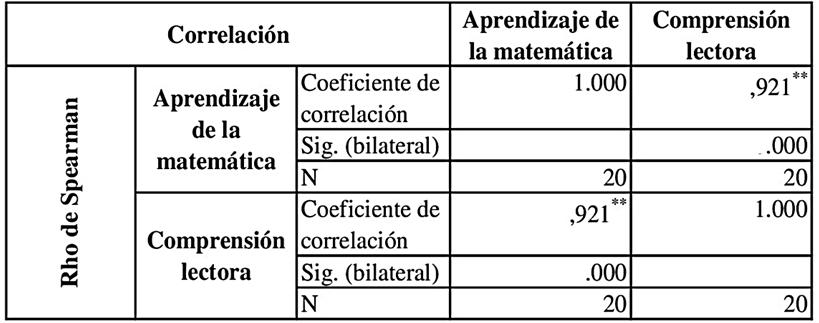
Se establecieron dos hipótesis para determinar la relación entre las variables, con un nivel de significancia del 0.05, el criterio para tomar una decisión se basa en el valor p (p-value), si el valor p ≤ 0.05, se rechaza la hipótesis nula (H₀) y se acepta la hipótesis alternativa (H₁), si el valor p > 0.05, no se rechaza la hipótesis nula (H₀). Previamente, se realizó un control de calidad de los datos para verificar su completitud. En función de determinar la distribución de los datos entre las variables se aplicó la prueba de Kolmogorov-Smirnov para la muestra, los resultados mostraron que los datos no seguían una distribución normal, por lo tanto, el análisis de las variables se realizó bajo la prueba de correlación Rho de Spearman para determinar la relación entre la comprensión lectora y el aprendizaje de la matemática en los estudiantes del subnivel superior (noveno) de la Escuela Océano Pacífico.

En la Tabla 1 se aprecia que la relación entre la comprensión lectora y el aprendizaje de las matemáticas reportada por el software estadístico SPSS es de 0,921. Al ser un valor cercano a 1 se afirma que existe una correlación positiva fuerte entre las dos variables. Dado que el valor p es menor a 0.05, se rechaza la hipótesis nula (H0) y se acepta la hipótesis alternativa (H1); es decir, existe correlación entre la comprensión lectora y el aprendizaje de las matemáticas.

Evaluaciones como las pruebas PISA que evalúa las habilidades y conocimientos de los estudiantes en lectura, matemáticas y ciencias, han demostrado la relación entre la comprensión lectora y las matemáticas. Según la ^{UNESCO (2023)}:

Las pruebas PISA han demostrado que Singapur se ha destacado en la comprensión lectora, matemáticas y ciencias. De igual manera, se ha evidenciado que otros países asiáticos como: Japón, Corea del Sur y Hong Kong ocupan posiciones altas dentro de estos procesos. Sin embargo, debido a la pandemia del COVID-19 se ha notado una disminución del promedio de matemáticas referente a 15 puntos a nivel mundial. (p. 34)

La comprensión lectora y el aprendizaje de las matemáticas se encuentran estrechamente relacionados; mientras mayor sea la comprensión lectora, mayor será el nivel de aprendizaje de las matemáticas. Sin embargo, la limitada muestra podría generar sesgos en la interpretación de los datos, por tanto, se recomienda ampliar el tamaño de la muestra e incluir instituciones educativas de diferentes contextos socioeconómicos y geográficos para mejorar la representatividad.

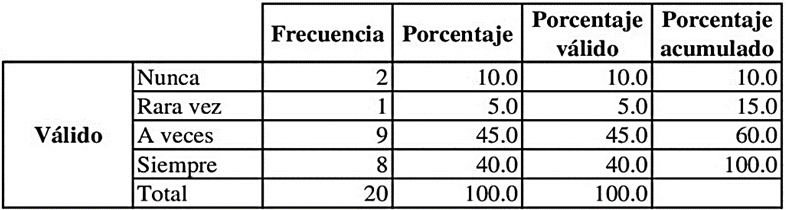
La comprensión lectora se asocia con la capacidad de lectura que los estudiantes desarrollan en etapas tempranas. Para ^{Carballo (2024}) la comprensión lectora resulta un factor clave para resolver problemas matemáticos. La Tabla 2 muestra la frecuencia en que los estudiantes necesitan leer más de una vez para comprender la acción a ejecutarse en los enunciados de los ejercicios matemáticos.

El 90 % de los participantes manifestó que necesita leer más de una vez para comprender el enunciado del ejercicio propuesto y solo un 10 % mostró un nivel de comprensión alta. Para ^{Montero y Mahecha (2020}) la mayoría de los estudiantes seleccionan datos numéricos sin tener presente la categoría a la que pertenecen. Existen palabras que se escriben de forma diferente, pero ejecutan la misma acción, como, por ejemplo: a la suma también se la conoce como adición, a la resta como sustracción o diferencia, a la multiplicación como producto y a la división como cociente.

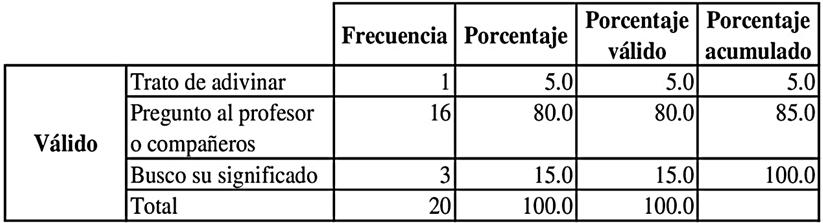
El análisis revela que el 40 % de los estudiantes requiere realizar múltiples lecturas en cada enunciado, debido a la terminología utilizada en las matemáticas para designar la acción del ejercicio. Este hecho resulta especialmente crítico dado que las matemáticas presentan un carácter acumulativo, lo que da como resultado que la comprensión de conceptos básicos se relaciona directamente con el aprendizaje. En la Tabla 3 se ilustran las acciones que realizan los estudiantes cuando se encuentran con palabras o conceptos poco conocidos.

De acuerdo con el análisis, el 80 % de los estudiantes optó por solventar sus dudas con el docente responsable de la asignatura y solo el 15 % fortaleció sus conocimientos con el aprendizaje autónomo. Este comportamiento coincide con lo señalado por ^{Alvarado (2023}), quien destaca que el aprendizaje independiente facilita la identificación de palabras clave, pero está limitado por los conocimientos previos del estudiante. ^{Balopiños y Ucang (2025}) revelan que, de un total de 50 estudiantes filipinos, el 48 % se clasifica como lectores independientes. Sin embargo, el 38 % requiere orientación para fortalecer su comprensión lectora, mientas que el 14 % se encuentra en un nivel de frustración, enfrentando desafíos que pueden derivar en su desconexión con el entorno educativo.

Por su parte, un rendimiento inferior en la comprensión lectora resalta la necesidad de implementar estrategias educativas efectivas para potenciarla y fomentar la participación de los estudiantes.

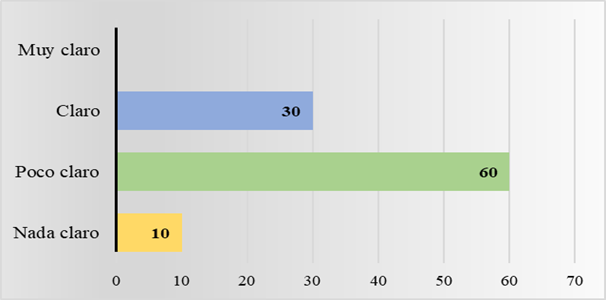
Para comprender las acciones realizadas por los estudiantes se realizó la siguiente pregunta: ¿Te resulta claro comprender las instrucciones de los problemas matemáticos? En la Figura 1, el 10 % de los estudiantes menciona que no comprende los enunciados de los ejercicios (Nada claro) y el 60 % poseyó una comprensión básica del contenido (Poco Claro), mientras que el 30 % mostró un nivel de comprensión alta (Claro). Es decir, el 70 % presentó dificultades para comprender los enunciados de los ejercicios matemáticos. ^{Alvarado (2023}) resalta que el 21 % de estudiantes colombianos posee una comprensión alta para resolver problemas matemáticos y solo un 3 % interpreta representaciones simbólicas.

Este hallazgo coincide con la investigación de ^{Mirondo et al. (2024}), quien manifiesta que solo el 4,24 % de un total de 118 estudiantes mostró una comprensión lectora alta; por otra parte, el nivel de resolución de problemas matemáticos se encontró por debajo del nivel intermedio, es decir, el 65,25 % de los estudiantes indicó un nivel principiante, por lo que solo pueden resolver problemas sencillos.

El desarrollo del pensamiento lógico y reflexivo constituye un elemento esencial para la resolución de problemas matemáticos. Para ^{Patiño et al. (2021}) “la resolución de problemas permite no sólo aprender Matemáticas, sino también desarrollar el pensamiento lógico de los estudiantes” (p. 461). Actualmente, la práctica de los ejercicios matemáticos se limita a la repetición continua de algoritmos y fórmulas para desarrollar capacidades y destrezas esenciales en torno a la resolución de problemas matemáticos.

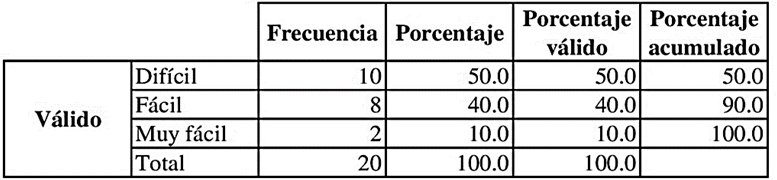
La Tabla 4 presenta el nivel de dificultad de los estudiantes para comprender y desarrollar ejercicios matemáticos, el 10 % no presentó mayor dificultad en comprender y desarrollar los ejercicios planteados, mientras que el 50 % mostró dificultades en la ejecución de los problemas matemáticos y el 40 % se situó dentro del rango normal, es decir, poseen un nivel de comprensión aceptable de la asignatura de la matemática. ^{Bustamante y Cabrera (2022}) resaltan que el 31 % de un total de 26 estudiantes presentaron dificultades para concentrase o se les dificultó hacer las tareas encomendadas. De acuerdo con ^{Balopiños y Ucang (2025}) hacer que las clases sean más interesantes y ayudar a los estudiantes cuando enfrentan dificultades es fundamental para desarrollar su perseverancia.

Investigaciones como las de ^{Akin (2022}) han demostrado que incluso los niños con habilidades matemáticas presentan dificultades para resolver ejercicios debido a la comprensión incorrecta del contenido del texto. La relación entre la comprensión lectora y el aprendizaje de las matemáticas difiere según el contenido matemático y la capacidad del estudiante para asimilar la información proporcionada.

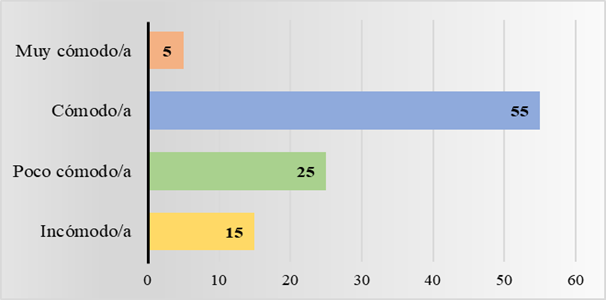
Al plantear la pregunta ¿Cómo te sientes al resolver problemas matemáticos?, en la Figura 2 se determinó que solo el 5 % se siente (Muy cómodo/a) al resolver los ejercicios y 55 % se siente (Cómodo/a), mientras que el 15 % se siente (Incómodo/a) y el 25 % se siente (Poco cómodo/a). Este hecho resalta que el nivel de comprensión de la matemática se encuentra influenciado por la actitud del alumno durante el proceso de aprendizaje. De acuerdo con ^{Bustamante y Cabrera (2022}) los factores emocionales conectados al rendimiento académico -motivación, aptitudes, ambiente escolar, capacidad de concentración, autoestima, estrés académico-, afectan el rendimiento académico de un 38 % de estudiantes de una clase. ^{Nahdi et al. (2024}) argumentan que los estudiantes que disfrutan de las matemáticas son más propensos a investigar nuevos enfoques o estrategias para resolver ejercicios, lo que contribuye al desarrollo de habilidades para analizar, formular y resolver de forma más eficiente.

El subrayado y las notas aclaratorias resultan estrategias para identificar aspectos claves dentro de un texto. De acuerdo con ^{Jara et al. (2022}) el subrayado es una técnica para resaltar ideas fundamentales, se realiza mediante de trazos, líneas o anotaciones en cualquier medio convencional para comprender de manera práctica el contenido de un texto.

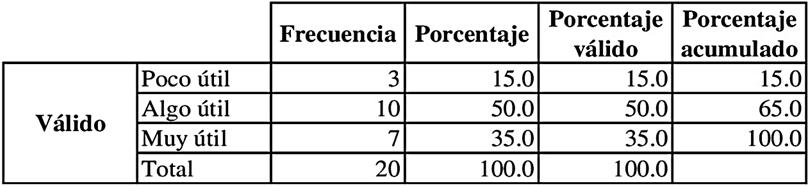
En la Tabla 5 se aprecia que estrategias como resaltar o subrayar las palabras clave dentro del texto son consideradas por el 15 % de los estudiantes como (Poco útiles) y el 50 % como (Algo útil). ^{Alvarado (2023}) en su investigación ejecutada en 42 escuelas demuestra que resaltar o subrayar las palabras no garantiza una mejor lectura y comprensión del contenido textual. Sin embargo, permite marcar aspectos importantes para tener en cuenta durante la resolución de un ejercicio, por ende, el 35 % de los estudiantes lo consideran como un factor (Muy útil) en el proceso de resolución de ejercicios matemáticos.

Para determinar si las estrategias de subrayado y anotaciones ayudan en la comprensión lectora y la resolución de ejercicios, se planteó la siguiente pregunta: ¿Crees que tu comprensión lectora se relaciona con la rapidez con la que resuelves los problemas matemáticos?

Como se visualiza en la Figura 3, el 65 % de los estudiantes menciona que la comprensión lectora se relaciona con la rapidez con la que desarrollan los ejercicios matemáticos, mientras que el 35 % restante considera que no es significativo. Estudios como el de ^{Karacaoğlu y Kasap (2023}) sustentan que la comprensión lectora es la variable más eficaz para predecir el rendimiento matemático de los estudiantes. Para ^{Malagón (2024}) 10 de 14 estudiantes muestran poco interés por la lectura debido a que se interesan en actividades extracurriculares.

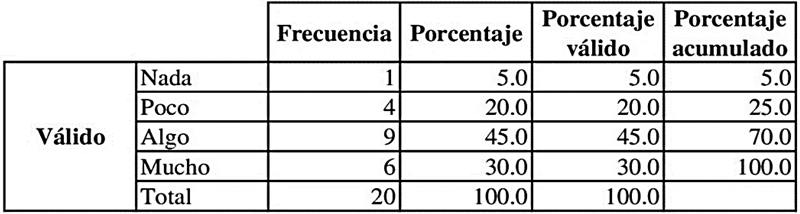
Considerar la capacidad del estudiante para resolver problemas matemáticos estableció la necesidad de plantear la siguiente pregunta: ¿Consideras que tu capacidad para interpretar problemas matemáticos es adecuada?

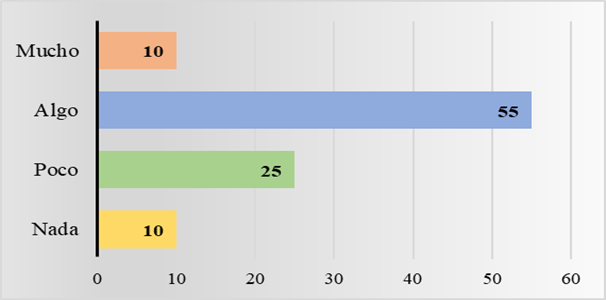
Según la Tabla 6, el 30 % de los estudiantes considera que su capacidad para interpretar problemas matemáticos es alta (Mucho), mientras que el 45 % mencionan que tiene una capacidad promedio (Algo). El 25 % de los estudiantes hacen referencia que su capacidad es bajo (Poco) y el 5 % considera que su capacidad para interpretar problemas matemáticos es deficiente (Nada). En concordancia con los hallazgos de ^{Bustamante y Cabrera (2022}), los autores mencionan que el 58 % de 26 estudiantes consideran que tienen una comprensión razonable de la asignatura. Por tal motivo, se planteó la siguiente pregunta: ¿Te sientes capaz de identificar correctamente los datos necesarios en un problema matemático?

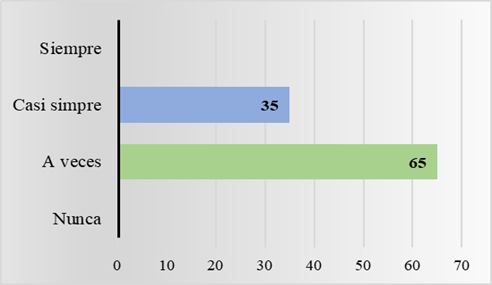
En la Figura 4, el 35% de los estudiantes muestran una seguridad de (Casi siempre) y el 65% (A veces), es decir, más de la mitad de los estudiantes siente inseguridad de su capacidad para interpretar y resolver problemas matemáticos, este factor hace referencia a la tabla 3 en relación con la recurrencia con la que los estudiantes realizan preguntas al docente a la hora de resolver los ejercicios propuestos. Estudios como el de ^{Supontawanit y Lertlit (2021}) demuestran que la comprensión lectora es un aspecto esencial en la resolución de problemas matemáticos, además, factores como el estado socioeconómico se relacionan con la capacidad de aprendizaje y la resolución de problemas matemáticos.

CONCLUSIONES

La relación entre la comprensión lectora y el aprendizaje de las matemáticas evidencia una correlación positiva fuerte entre las dos variables estudiadas al reportar un valor de 0,921. Este resultado indica que a medida que aumenta la comprensión lectora, se incrementa también el nivel de aprendizaje de las matemáticas.

El análisis de los datos refleja que el 40 % de los participantes requiere realizar múltiples lecturas para comprender la acción solicitada. Además, el 80 % de los participantes recurre al docente como principal fuente para solventar dudas, lo que evidencia una alta dependencia del apoyo externo durante el proceso de aprendizaje.

En relación con el nivel de dificultad en la resolución de ejercicios matemáticos, el 50 % presenta dificultades para resolver problemas matemáticos, mientras que el 40 % se encuentra en un rango aceptable de comprensión y desarrollo de ejercicios. Por otra parte, las estrategias de comprensión lectora como el subrayado y las notas aclaratorias son consideradas como (Muy útiles) por el 35 % de los estudiantes, mientras que el 50 % las encuentra (Algo útiles). Estos resultados destacan que un aumento de la comprensión lectora favorece el aprendizaje de las matemáticas.

Por ende, el 75 % de los encuestados percibe que su capacidad para interpretar problemas matemáticos es adecuada, sin embargo, un 25 % manifiesta que su capacidad de interpretación es deficiente.

Las técnicas del subrayado e identificación de palabras clave durante la resolución de ejercicios matemáticos promueven el estudio independiente del estudiante, además, reducen la dependencia del docente. Sin embargo, es importante reconocer las limitaciones del estudio, como el uso de una muestra limitada y su alcance, hecho que resalta la necesidad de aplicar otros métodos de estudio para profundizar la relación entre comprensión lectora y aprendizaje de las matemáticas