INTRODUCCIÓN
La Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCO), organismo encargado de guiar los esfuerzos globales hacia la paz y la seguridad mundial desde la educación, la ciencia y la cultura, elaboró un programa con objetivos para ser cumplidos hasta el año 2030 para el Desarrollo Sostenible. En ese programa se plantea como objetivo número 4, garantizar una educación inclusiva y equitativa de calidad y promover oportunidades de aprendizaje permanente para todos.
El programa se encuentra vinculado directamente con la necesidad de fomentar los procesos educativos a nivel mundial, en dos direcciones fundamentales: la primera aumentar el acceso y la segunda incrementar la calidad de estos procesos. Dentro del marco de acción propuesto para su consecución, Declaración de Incheón, UNESCO (2016) se reconoce la necesidad de fortalecer la educación en las ciencias y en particular la matemática.
A partir de esta necesidad a nivel mundial existe un creciente interés por el perfeccionamiento del proceso de enseñanza aprendizaje (PEA) de la Matemática. Otro elemento impulsor de este interés es la creciente matematización del mundo actual, en el que se pretende que el ciudadano del siglo XXI sea capaz de:
• tomar decisiones comparando y analizando datos estadísticos;
• interpretar el significado de proposiciones con contenido matemático y sus implicaciones para la supervivencia humana; y de
• resolver problemas donde tenga que emplear conocimientos matemáticos
El PEA de la asignatura Matemática debe preparar a los estudiantes para que al egresar de las escuelas se inserten como ciudadanos en la llamada sociedad de la información. Además, como asignatura en el currículo del preuniversitario debe contribuir a hacer evidente sus implicaciones en la vida, elemento fundamental de la competencia matemática. En Cuba se reordenan los contenidos de la asignatura y se perfeccionan los métodos, pero el cambio fundamental radica en que la formulación y solución de problemas se convierte en el eje central de trabajo con sus contenidos y debe contribuir a hacer evidente las implicaciones de la matemática en la vida.
Como resultado de indagaciones empíricas realizadas por los autores en su práctica pedagógica, se observa que los estudiantes de preuniversitario presentan dificultades con los contenidos matemáticos y con su utilización en situaciones reales.
En la búsqueda de las causas fundamentales se evidencia que en el proceso de enseñanza aprendizaje no se logra una comprensión por los estudiantes de los conceptos matemáticos y su relación con situaciones de la vida. La bibliografía utilizada en el proceso carece de problemas con situaciones reales y no se es sistemático al proponer problemas en clases relacionados con las mismas. De ahí que, se hace necesario proponer problemas con aplicaciones de las funciones numéricas que desarrollen la competencia matemática de los estudiantes, para ello se selecciona la Unidad 2: Ecuaciones y funciones exponenciales y logarítmicas del undécimo grado en Cuba.
METODOLOGÍA
El presente artículo de investigación responde al enfoque de investigación cuantitativo, Hernández, Fernández y Baptista (2010), aunque se combina con lo cualitativo. En su desarrollo se utilizan métodos del nivel teórico, del nivel empírico y del nivel estadístico. Se utilizó el análisis de documentos, la observación, la entrevista, la encuesta, el experimento, la triangulación de fuentes, el criterio de especialista, la estadística descriptiva y la prueba de hipótesis Wilcoxon de los rangos con signos para muestras relacionadas.
En correspondencia con los métodos se elaboraron y aplicaron instrumentos para la recolección de datos tales como: guía para el análisis de documentos, guía de observación, guía de entrevista, cuestionario, guía para la valoración de la propuesta por especialistas y la prueba pedagógica.
En un primer momento, se determinan los referentes teóricos esenciales para lo que se realiza fundamentalmente el análisis de documentos y la triangulación de fuentes. Luego, se determinan las necesidades y potencialidades de la muestra y se elabora una primera versión de los problemas con aplicaciones de las funciones numéricas, la que es sometida a criterio de especialistas y, en correspondencia, se perfecciona.
Posteriormente, se utilizan los problemas en la asignatura Matemática en la Unidad 2: Ecuaciones y funciones exponenciales y logarítmicas, en un grupo de 30 estudiantes de undécimo grado de preuniversitario del municipio de Santa Clara, que se toma como muestra intencional de una población de 132 estudiantes de ese grado.
Para constatar los resultados, se utiliza el experimento, con un diseño preexperimental de tipo O1 X O2, en el que se evalúa el desarrollo de habilidades que constituyen indicadores de la competencia matemática. Finalmente, se aplica la Prueba de Wilcoxon de los rangos con signos para muestras relacionadas para el análisis comparativo de las transformaciones experimentadas.
RESULTADOS Y DISCUSIÓN
Delors et al. (1996) plantean el aprendizaje a lo largo de toda la vida como una necesidad para la sociedad actual, donde se aprovechen las potencialidades educativas de cada uno de los contextos en los que se desarrolla el individuo. Para el logro de este objetivo las Comunidades Europeas (2007) seleccionan las competencias claves, dentro de las cuales se encuentra la competencia matemática definida como:
(…)
. (Comunidades Europeas 2007:6)la habilidad para desarrollar y aplicar el razonamiento matemático con el fin de resolver diversos problemas en situaciones cotidianas. Basándose en un buen dominio del cálculo, el énfasis se sitúa en el proceso y la actividad, aunque también en los conocimientos. La competencia matemática entraña -en distintos grados- la capacidad y la voluntad de utilizar modos matemáticos de pensamiento (pensamiento lógico y espacial) y representación (fórmulas, modelos, construcciones, gráficos y diagramas)
Dicha competencia también ha sido definida por Godino, Giacomone, Batanero y Font (2017) como la habilidad para entender, juzgar, hacer y usar las Matemáticas en una variedad de contextos y situaciones intra y extra‐matemáticas en los que las Matemáticas juegan o podrían jugar su papel.
Ambas definiciones parten del concepto habilidad y se centran en el uso de la Matemática. La primera menciona las habilidades para calcular y representar, utilizar el pensamiento lógico y las diferentes formas de representación. La segunda se centra en los contextos y situaciones en las que se puede desarrollar la competencia matemática.
La definición dada por OCDE (2017) sobre esta competencia la identifica como una capacidad y extiende su significado hacia otros elementos más allá del uso de la Matemática en el mundo, tales como identificar y comprender el papel de la Matemática y emitir juicios bien fundados. Esta definición destaca el papel de dicha competencia en la vida personal del ciudadano constructivo, comprometido y reflexivo.
Estas definiciones a criterio de los autores no satisfacen los presupuestos de la presente investigación, pues entendemos que la competencia no es ni habilidad ni capacidad, sino configuración psicológica compleja. Por lo que se realiza una definición de competencia matemática como: configuración psicológica compleja integrada por conocimientos matemáticos, habilidades, procedimientos y estrategias matemáticas, que -de conjunto con componentes metacognitivos, motivacionales y cualidades de la personalidad- autorregulan el desempeño real y eficiente al resolver problemas cotidianos, entender el mundo, y tomar decisiones como un ciudadano constructivo, comprometido y reflexivo.
Dentro de las principales transformaciones realizadas a la Matemática como asignatura en Cuba se encuentra el establecimiento de lineamientos o ideas claves para el trabajo de la asignatura a partir del curso escolar 2004-2005. Dentro de los mismos se encuentra un punto fundamental:
. (Álvarez, Almeida & Villegas 2014:1)Plantear el estudio de los nuevos contenidos matemáticos en función de resolver nuevas clases de problemas, de modo que la resolución de problemas no sea solo un medio para fijar, sino también para adquirir nuevos conocimientos sobre la base de un concepto amplio de problema
Esto convierte a la formulación y resolución de problemas tanto intra como extra matemáticas, en el eje central del trabajo con los contenidos de la asignatura Álvarez et al. (2014). Estos deben contribuir a la formación integral de los estudiantes y como forma para adquirir y consolidar el saber y el saber hacer matemáticos.
Para poder desarrollar adecuadamente el proceso de enseñanza aprendizaje de la Matemática es necesario contar con docentes preparados. Relacionado con esto, Giné de Lera y Deulofeu (2014) analizan el papel que tiene la formación y la experiencia del profesorado de matemática sobre el conocimiento y las creencias en la solución de problemas.
El papel de la solución de problemas como método para la enseñanza de la Matemática es importante pues (…) “
.” (Defaz 2017:17)sirve para el desarrollo de procesos didácticos con múltiples formas de ejercitar y reflexionar sobre procesos, como son, la inducción, la deducción, la generalización y la particularización que son las claves del pensamiento Heurístico
Es importante mantener la curiosidad y el entusiasmo de los estudiantes por la solución de problemas matemáticos, por lo que se debe garantizar que estos se le presenten ordenados según su complejidad. (…) “
” (Meza-Cascante, Suárez-Valdés-Ayala & Agüero-Calvo 2015:67).parece recomendable que los docentes propongan problemas matemáticos a sus estudiantes con una dificultad incremental, iniciando con problemas de fácil comprensión que les ofrezcan una mayor probabilidad de ser resueltos exitosamente
Una dificultad presente en el proceso de enseñanza-aprendizaje de la Matemática radica en la ansiedad de los estudiantes en este proceso, demostrada en los estudios de Ramirez, Chang, Maloney, Levine & Beilock (2016). A criterio de los autores, una vía para enfrentarse a ella es precisamente utilizar problemas en orden creciente de dificultad y que estén vinculados con las motivaciones del estudiante.
“
” (Santos 2016:337) .El proceso de resolver problemas o comprender un concepto matemático involucra ciclos iterativos de discusión y colaboración en los que los estudiantes deben tener la oportunidad de expresar, revisar, contrastar, interpretar y refinar sus ideas y métodos de solución
Estos ciclos permiten que, mediante este proceso, se adquieran y fijen conocimientos y se desarrolle la competencia matemática. Al enfrentarse a la solución de un problema, este se puede considerar un desafío en el que los estudiantes desarrollan sus habilidades matemáticas y su creatividad, esto “conlleva mejoras en el comportamiento, en las habilidades sociales, la motivación, la autoestima y el rendimiento en todos los aspectos” (Ayllón, Gómez & Ballesta-Claver 2016:186).
Además, según Berenguer, Sánchez y Noguerol (2017) tiene potencialidades para formar el valor perseverancia en los estudiantes, para lo cual proponen una estrategia didáctica. La solución de problemas según Cruz (2002) facilita la asimilación de nuevos conocimientos, y desarrolla formas peculiares de interrelación con la sociedad y el ambiente.
La solución de problemas matemáticos ha sido investigada con profundidad por Polya (1945), quien propone un modelo dividido en cuatro etapas que constituye la base de varios modelos actuales. Ballester et al. (1992) en su libro Metodología de la Enseñanza de la Matemática realizan un estudio de cómo enseñar a resolver problemas y a insertar este proceso en el PEA de la asignatura Matemática. Pozo y Postigo (1994) explican la solución de problemas como contenido procedimental, generalizable a la asignatura Matemática.
Por su parte, Campistrous Pérez y Rizo Cabrera (2013) discuten cómo puede lograrse el trabajo con verdaderos problemas en las condiciones del aula. Por su parte, Parra y Breda (2017) evidencian las concepciones que poseen los profesores de matemática en formación de una universidad chilena, sobre la resolución de problemas y cómo la implementan en el desarrollo de sus clases. Celi, Hinojosa y Marín (2017) proponen una metodología basada en la de Polya (1945) para la resolución de problemas matemáticos.
También Liljedahl, Santos-Trigo, Malaspina y Bruder (2016) explican la relevancia de la heurística en los enfoques de resolución de problemas, la importancia de que los alumnos formulen y resuelvan sus propios problemas y el papel desempeñado por el uso de las TIC en este proceso. Binotto (2019) propone la utilización de una metodología de solución de problemas para la enseñanza de la estadística.
Mientras que Avvisati y Borgonovi (2020) realizan un estudio sobre el papel de los test en la educación, principalmente en el aprendizaje de la solución de problemas mediante test, demostrando que durante la realización de los mismos también los estudiantes aprenden sobre la solución de problemas.
El concepto de problema matemático no es el mismo para todos los investigadores. Un problema matemático “(...)
” (Ballester et al. 1992:447).es un ejercicio que refleja, determinadas situaciones a través de elementos y relaciones del dominio de las ciencias o la práctica, en el lenguaje común y exige medios matemáticos para su solución
Esta definición tiene como limitante que no toma en cuenta la necesidad de que la vía de solución debe ser desconocida y el papel del interés del solucionador al enfrentarse al problema.
Para resolver la limitante anterior y generalizar el concepto se define problema como “Toda situación en la que hay un planteamiento inicial y una exigencia que obliga a transformarla. La vía de solución tiene que ser desconocida y la persona quiere realmente realizar la transformación” (Rizo & Campistrous 1999:32), esta definición es aplicable a cualquier clase de problema.
La definición a la que se adscribe García-García (2019) es bastante similar a las anteriores al coincidir con la existencia de una demanda o acción a realizar, una persona que quiere o necesita satisfacer esa demanda y un proceso desconocido para cumplir con la misma, y a diferencia de los anteriores sí menciona el resultado al explicitar que puede tener uno, varios o ningún resultado. Atendiendo a los objetivos de esta investigación, los autores asumen la concepción de Rizo y Campistrous (1999) antes mencionada.
También existen diversos puntos de vista para clasificar los problemas. Cruz (2002) clasifica los problemas escolares de Matemática en problemas de aplicación y problemas puramente matemáticos, que se subdividen a su vez en problemas aritméticos, algebraicos y geométricos en dependencia de a cuál de los campos anteriores pertenecen los recursos empleados para su solución.
Para Cruz (2002) los problemas de aplicación son aquellos que surgen o pueden producirse en la práctica cotidiana, al constituir una simulación de la realidad o de una esfera de la misma y para su solución es necesaria la aplicación de herramientas o medios matemáticos. Esta tipología de problemas se adecua a los preceptos de esta investigación, ya que la competencia matemática implica aplicación de la matemática en diversas esferas.
Entre los contenidos matemáticos de amplia aplicación se encuentran las funciones y dentro de ellas las exponenciales y logarítmicas; ambas se imparten en el undécimo grado del preuniversitario cubano. Estas tienen grandes aplicaciones pues sirven de modelo para el análisis del crecimiento poblacional de los seres vivos, la expansión de una enfermedad en una población y para calcular la velocidad de caída de cuerpos considerando la resistencia del aire. Otras aplicaciones son los modelos de decaimiento radioactivo y para la determinación de la concentración másica de algunas sustancias. Además, se utilizan en la medicina, la astronomía, entre otras.
Según todo lo antes expuesto se defiende la idea de que es necesario que el proceso de enseñanza aprendizaje de las funciones numéricas se realice desde la solución y formulación de problemas, donde se vea de forma explícita sus múltiples aplicaciones para contribuir al desarrollo de la competencia matemática de los estudiantes.
NECESIDADES Y POTENCIALIDADES DE LA APLICACIÓN DE FUNCIONES NUMÉRICAS
La determinación de necesidades y potencialidades de la aplicación de las funciones numéricas en el undécimo grado se realiza a partir del análisis de documentos, la observación y la encuesta a docentes, directivos y a estudiantes.
El análisis de documentos incluye el programa director de Matemática, los programas de Matemática vigentes en el curso 2016-2017, las Resoluciones del Ministerio de Educación que norman el trabajo en el Preuniversitario y el libro de Matemática undécimo grado. Para la aplicación de la encuesta se selecciona una muestra de 30 estudiantes de undécimo grado de un preuniversitario de Santa Clara, 10 profesores de Matemática de undécimo grado del nivel preuniversitario de Santa Clara y 3 directivos de este nivel. La observación se realiza a cinco turnos de clases de Matemática.
Para el estudio de los documentos normativos se procede a determinar dos indicadores a tener en cuenta para su análisis: la orientación de la aplicación de las funciones numéricas en la asignatura Matemática en el nivel medio superior y la presencia de la solución de problemas con aplicaciones de las funciones numéricas.
El programa director de Matemática vigente desde el curso 1997-1998, orienta en los objetivos solucionar problemas en los que se apliquen los conocimientos y habilidades adquiridos sobre el significado de las operaciones de cálculo, la proporcionalidad y el tanto por ciento. También indica identificar relaciones funcionales y sus propiedades, a partir de tablas, diagramas, ecuaciones, gráficas u otras formas de representación, y utilizarlas en la modelación de situaciones prácticas.
Los programas de Matemática de Preuniversitario (MINED 2005, 2006a, 2006b), tienen entre sus objetivos resolver problemas relacionados con el desarrollo económico, político y social, local, nacional, regional y mundial y con fenómenos y procesos científicos-ambientales, que requieran conocimientos y habilidades relativos, entre otros, a las funciones y las funciones elementales.
El análisis del Programa de la asignatura en el undécimo grado permite constatar que en la Unidad 2 se orienta
Transferir de una representación a otra de las funciones exponenciales y logarítmicas, es decir, de sus propiedades a su representación analítica, gráfica o descriptiva (en el lenguaje común) y viceversa, aplicando estos conocimientos a situaciones sencillas de la práctica y otras ciencias. (MINED 2005:18)
Las orientaciones metodológicas tienen poca información sobre su tratamiento.
Al analizar el libro de Matemática de undécimo grado, elaborado por Campistrous et al. (1990), se observa que no existen problemas con aplicaciones de las funciones exponenciales y logarítmicas, solamente se hace referencia a las aplicaciones de los logaritmos a partir de los ejemplos 8 y 9 (Campistrous et al. 1990:32-33), en contradicción con los objetivos generales de la asignatura para el nivel, el grado y la unidad.
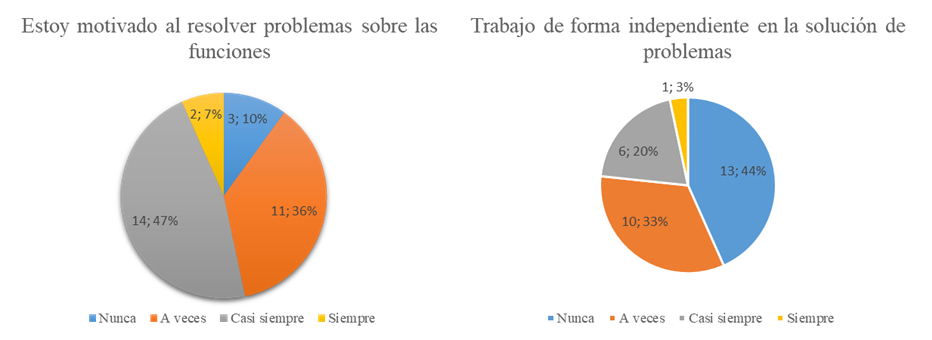
La encuesta se realiza a 30 estudiantes de undécimo grado de Santa Clara. En la pregunta sobre la motivación durante las clases de Matemática para la realización de los problemas sobre las funciones, se constató que un 6,7% de los estudiantes siempre resultaron motivados, el 46,7% casi siempre, el 36,7% a veces y un 10,0% nunca se sintió motivado (Figura 1). Estos resultados indican que se debe trabajar en este sentido pues un 46,7% de los estudiantes expresaron que se sienten motivados hacia la solución de los problemas sobre funciones con baja frecuencia.
Sobre la posibilidad de responder de forma independiente los problemas sobre funciones en las clases, se constató que siempre solo el 3,3% de los estudiantes son capaces de responder por sí solos, el 20% casi siempre, un 33,3% a veces y un 43,3% nunca. Esta información ofrece datos sobre las habilidades que traen los estudiantes y los hábitos de trabajo independiente, donde hay carencias en un 76,7% de los estudiantes, que se ubican en las categorías nunca y a veces.
En la pregunta sobre las aplicaciones de las funciones numéricas en la vida se constató que el 26,7% conoce alguna de ellas y el 73,3% no las conoce. Este aspecto influye en el desarrollo de la investigación profundizando el interés del investigador.
A la interrogante sobre la frecuencia de solución en clases de problemas con aplicaciones de las funciones el 3,3% respondió frecuentemente, el 86,7% responde ocasionalmente y el 10,0% nunca (Figura 2).
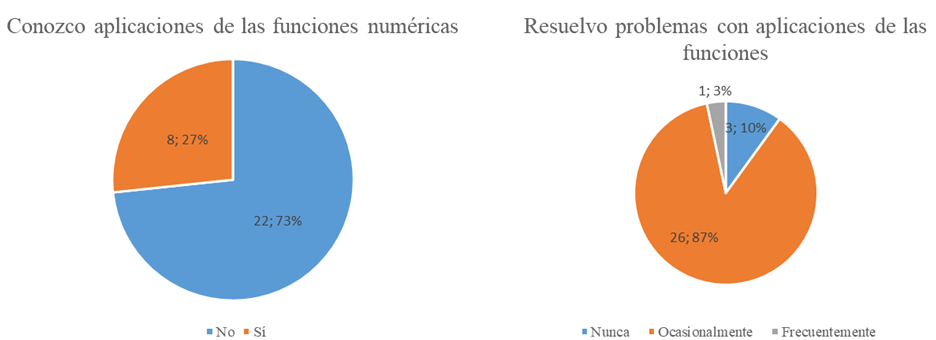
Fuente: Elaboración propia
Figura 2: Resultados sobre la frecuencia de solución de problemas y el conocimiento de las aplicaciones de las funciones numéricas
Sobre las principales limitaciones (Figura 3) que a criterio de los estudiantes afectaron la realización de problemas sobre funciones, el 43,3% de los estudiantes contestó que no entendían claramente el concepto de función, el 70,0% planteó contar con pocos problemas en el libro de Matemática de undécimo grado, el 40,0% coincidió en que los problemas están dirigidos para todos los estudiantes por igual, un 70,0% se refirió a la poca sistematización y el 73,3% destacó la carencia de una colección de problemas. Además, el 60 % reconoció dificultades al comprender el problema y modelar la situación.
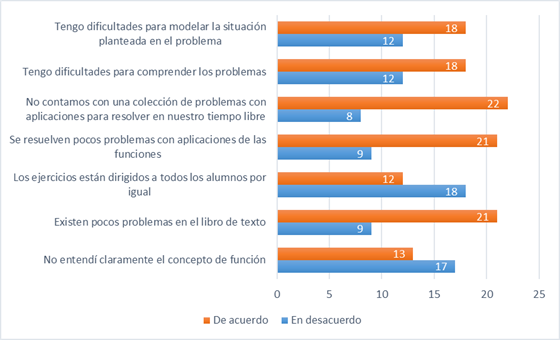
Fuente: Elaboración propia
Figura 3: Principales limitaciones que afectan la solución de problemas con aplicaciones de las funciones a criterio de los estudiantes
En la encuesta a docentes participan un total de 10 y ofrece como resultados los siguientes.
La primera interrogante en la que se le pide que escriban aplicaciones de varias funciones, el 90% conoce aplicaciones de las funciones lineales, cuadráticas, logarítmicas y trigonométricas y el 70% conoce aplicaciones de la función exponencial.
En la segunda interrogante sobre las orientaciones metodológicas de la asignatura sobre el tema, el 80% plantea que existen, el 10% que no existen y el resto (10%) no responde. El 50% de los encuestados plantea que son insuficientes en todos los grados.
A la interrogante relacionada con la preparación sobre el tema, el 50% plantea que sí recibió preparación y el resto que no la ha recibido. El 60% plantea que considera su preparación insuficiente y que necesitan profundizar en el tema.
El 40% afirma que utiliza frecuentemente problemas con aplicaciones en sus clases y el 60% que lo hace ocasionalmente. El 70% plantea que propone a sus estudiantes que investiguen sobre las aplicaciones de las funciones, para que profundicen y comprendan mejor la temática y el 20% no lo hace.
El 100% considera pertinente que los estudiantes conozcan sobre el tema como una necesidad para la vida, para una mayor comprensión de la naturaleza y la vida práctica. Aunque plantean como principal dificultad la falta de bibliografía en la que se analice con profundidad la aplicación de las funciones numéricas.
La observación realizada en un total de cinco clases en las que asistieron todos los estudiantes ofrece los siguientes resultados (Tabla 1):
En el aspecto relacionado con la participación de los estudiantes en la clase de Matemática, se observa que el 40% participa activamente en las clases, el 53,3% lo hace esporádicamente, fundamentalmente cuando les interesa la temática de la clase, y el resto (6,7%) de los estudiantes no participa a menos que el profesor le pida que lo haga.
Atendiendo al uso o no por el profesor de problemas con aplicaciones de las funciones en las clases observadas, el profesor no utiliza ningún problema con aplicaciones de las funciones. Al no usar las aplicaciones de las funciones, los estudiantes no manifiestan interés por las mismas.
El 23,3% de los estudiantes abandonan la solución de los problemas luego de un primer intento fallido esperando a que los demás estudiantes respondan por ellos. El 6,7% de los estudiantes llega a la solución tras un primer intento. El resto (70,0%) lo intenta varias veces. El 36,7% del grupo llega al resultado final.
Los directivos expresan en las entrevistas realizadas la pertinencia de un trabajo encaminado a la solución de problemas con aplicaciones de las funciones numéricas; argumentan que el mismo contribuye de manera significativa al cumplimento de los objetivos del nivel, ya que permite que los estudiantes aprendan las propiedades de las funciones numéricas desde sus aplicaciones al ver las implicaciones de estas a la realidad.
La triangulación de las fuentes permite plantear que en los programas de la asignatura se expresa como uno de sus objetivos el estudio de los contenidos matemáticos, específicamente las funciones numéricas, a partir de sus aplicaciones en la vida. En los libros de texto son insuficientes los problemas con estas características, particularmente en el libro de texto de undécimo grado, donde solo aparecen problemas relacionados con la función logarítmica.
Por otra parte, el uso de estos problemas es poco frecuente en el proceso de enseñanza aprendizaje de las funciones numéricas. Aunque los profesores consideran pertinente la preparación de los estudiantes sobre el tema, plantean como una dificultad la falta de bibliografía.
PROBLEMAS CON APLICACIONES DE LAS FUNCIONES NUMÉRICAS
La propuesta consiste en problemas que evidencian la aplicación de las funciones numéricas, que responden a los contenidos de la Unidad 2 “Ecuaciones y funciones exponenciales y logarítmicas” del undécimo grado y que complementan el libro de texto de ese grado. A continuación, se presentan cinco ejemplos de estos problemas.
Al iniciar el año 2017 un cuentapropista deposita 5000,00 CUP en un banco, con una tasa de interés del 6%. Si los intereses se acumulan anualmente y esta situación se modela a partir de la siguiente función C F =5000 1+ 6 100 t donde C F es el capital final y t es el tiempo medido en años.
¿Cuántos CUP tendrá al cabo de 1 año?
Al cabo de 2 años el cuentapropista extrae las ganancias y cambia el tipo de cuenta. Ahora acumula interés cada seis meses y el modelo es el siguiente C F =5000 1+ 6 200 2t . ¿Cuántos CUP tendrá un año después del cambio?
La edad de un objeto antiguo se puede determinar por la cantidad de carbono 14 radiactivo que permanece en él. Si D 0 es la cantidad original de carbono 14 y D es la cantidad restante, entonces la edad A del objeto (en años) se determina por A D =−3580log D D 0 .
Calcule la edad de un objeto si la cantidad D de carbono 14 que permanece en el objeto es 75% de la cantidad original D 0 .
Cierto cultivo de bacteria Bacillus anthracis inicialmente tiene una bacteria y se observa que se duplica cada media hora.
Determine un modelo exponencial n t = n 0 2 t α para el número de bacterias en el cultivo después de t horas
Antes de concluir la jornada laboral (8 horas) un investigador quiere saber cuántas bacterias tenía en el cultivo.
Represente esta función gráficamente utilizando el software “Geogebra”.
Cierta cepa de bacterias se divide cada tres horas. Si una colonia comienza con 50 bacterias, entonces el tiempo t (en horas) requerido para que la colonia crezca a N bacterias se expresa como t N =10log N 50 .
¿Qué tiempo demoraría la colonia en llegar a un millón de bacterias?
La escala de Richter es utilizada para determinar la magnitud de los terremotos. En el año 2016 se produjo un terremoto de gran intensidad en Ecuador con una magnitud de 7,8 en la escala de Richter. En ese propio año se registró un sismo perceptible, en Santiago de Cuba de magnitud 4,5, en la propia escala. Esta escala está dada por la función I x =log x S donde I es el valor en la escala, x es la intensidad del terremoto y S es una constante ¿Cuántas veces fue mayor la intensidad del registrado en Ecuador comparado con el registrado en Santiago de Cuba?
Esta propuesta se encuentra ordenada en un grado creciente de dificultad. En ella se reflejan situaciones relacionadas con el contexto en el que viven los estudiantes y su orientación profesional. Durante la realización de estos problemas el profesor debe explicar las implicaciones del contenido matemático en las situaciones dadas.
En particular, la propuesta desarrolla la competencia matemática de los estudiantes atendiendo al desarrollo de habilidades tales como identificar, calcular, evaluar y comparar, y la adquisición de conocimientos matemáticos y de otras ciencias.
VALORACIÓN DE LA PROPUESTA DE PROBLEMAS POR ESPECIALISTAS
La propuesta se somete a criterios de especialistas para evaluar la pertinencia y la factibilidad de su puesta en práctica. Para ello se tuvo en consideración: la determinación de los aspectos esenciales a evaluar y la selección de los especialistas. Se seleccionan diez según su experiencia como profesores de Matemática (más de 10 años), su nivel profesional y académico.
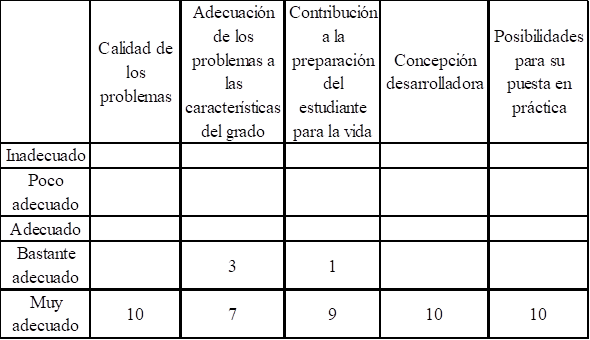
Una vez recopilada y analizada la información ofrecida por estos, se precisan aspectos importantes que permitieron el perfeccionamiento de los problemas elaborados a partir del rigor científico de los señalamientos realizados. En la valoración de la propuesta de los problemas para la aplicación de las funciones numéricas, los especialistas consideran (Table 2):
El aspecto 1, sobre la calidad de los problemas, fue evaluado como muy adecuado por el 100% de los especialistas. No se realizan argumentaciones, ni observaciones al respecto.
La evaluación a la adecuación de los problemas a las características del grado, aspecto 2, fue considerada de muy adecuado por el 70% de los especialistas consultados. El resto lo evaluó como bastante adecuado (30%). Dos señalan las dificultades que pueden presentar los estudiantes en el trabajo algebraico y las propiedades de las potencias. El aspecto 3, en el que se solicitaban valoraciones sobre la contribución a la preparación del estudiante para la vida, recibió la categoría muy adecuado por el 90% de los especialistas, el resto lo evaluó como bastante adecuado (10%). La concepción desarrolladora de la propuesta, aspecto 4, recibió valoraciones de muy adecuado por los 10 especialistas (100 %). Finalmente, el aspecto 5 referido a las posibilidades para su puesta en práctica, fue evaluado como muy adecuado por el 100% de los especialistas.
Los especialistas señalaron elementos como posibles dificultades para su empleo en el PEA de la Matemática los relacionados con el trabajo algebraico por los estudiantes. Recomiendan el uso de la notación científica y mayor empleo de las TIC para racionalizar el trabajo mental. Estos aspectos fueron mejorados en la propuesta final.
Además, como elemento positivo valoran que los problemas en cuestión pueden mejorar el aprendizaje del tema, pues acercan las funciones numéricas a elementos que los estudiantes conocen del estudio de otras ciencias y son de su interés, y promueven un aprendizaje significativo.
El análisis integrador de los aspectos sometidos al criterio de los especialistas permite determinar la aceptación de los problemas propuestos como tendencia, pues las opiniones emitidas se ubican en las categorías de adecuado y muy adecuado, lo que ratifica las posibilidades de aplicación de la propuesta y su factibilidad en el contexto pedagógico para el que ha sido concebida.
DESARROLLO DE LA COMPETENCIA MATEMÁTICA EN UN GRUPO DE ESTUDIANTES DE PREUNIVERSITARIO
Con vistas a evaluar el desarrollo alcanzado en indicadores de la competencia matemática, se realiza un pre-experimento en un grupo de treinta estudiantes de undécimo grado de un preuniversitario de Santa Clara. Durante el pre-experimento también se recogen opiniones de los estudiantes. Se aplica una prueba pedagógica en dos momentos: al comenzar a recibir la Unidad 2, y al concluir la misma (Figura 4).
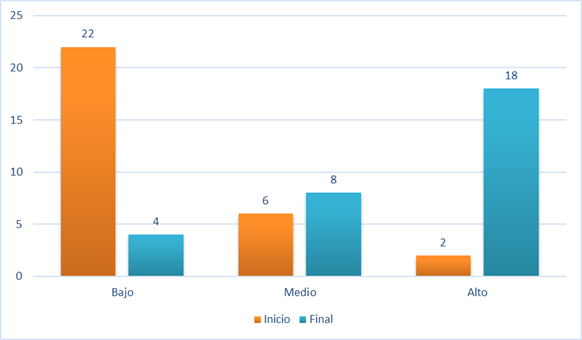
Al inicio del proceso, la habilidad más afectada es resolver problemas, pues un 93,3% de los estudiantes presentan dificultades y la menos afectada es la habilidad identificar con un 36,7% de estudiantes afectados. Según el desarrollo alcanzado en las habilidades evaluadas, se clasifican a los estudiantes en las categorías de alto, medio y bajo, obteniéndose como resultados los siguientes: bajo 73,3% de los estudiantes, medio 20,0% y alto 6,7%.
Al concluir la unidad, se manifiesta una tendencia ascendente en el desarrollo de habilidades que constituyen indicadores de la competencia matemática. Sin embargo, a pesar del avance, formular pasa a ser la más afectada con un 20,0% de estudiantes desaprobados. La mayor mejoría se encuentra en la habilidad resolver problemas y los mejores resultados se logran nuevamente en la habilidad identificar con solo un 3,3 % de los estudiantes afectados. En cuanto al desarrollo general en las habilidades un 13,3% estudiantes se ubica en el nivel bajo, 26,7% en medio y 60% en alto.
Si bien al inicio la mayor cantidad de estudiantes presentaba dificultades al identificar, enunciar, calcular, formular, esbozar y resolver problemas, con el desarrollo del proceso de enseñanza aprendizaje de las funciones numéricas mediante problemas donde se explicitan sus múltiples aplicaciones, se produce un movimiento que conlleva a que disminuya el número de estudiantes con dificultades en las habilidades que constituyen indicadores de la competencia matemática. Como consecuencia de este movimiento disminuye el porcentaje del nivel bajo y aumenta el de los niveles medio y alto (Figura 5).
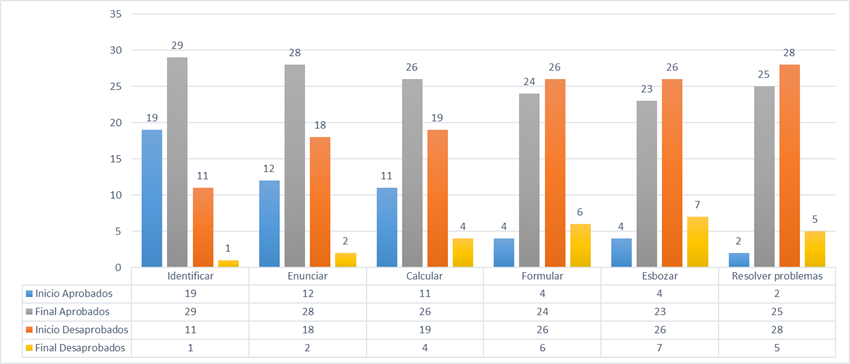
Fuente: Elaboración propia
Figura 4: Resultados del pre experimento: comportamiento por habilidades.
Para el análisis comparativo de las transformaciones experimentadas en el desarrollo de habilidades que constituyen indicadores de la competencia matemática, al finalizar el pre-experimento se aplica la Prueba de Wilcoxon de los rangos con signos para muestras relacionadas. En su aplicación se tuvo en cuenta que se trata de muestras dependientes, el mismo grupo antes y después, y que los datos son discretos.
En la prueba se comparan los valores obtenidos en las evaluaciones inicial y final, y se determina si los cambios ocurridos en relación con el desarrollo de habilidades son significativos o no. Para su aplicación se consideró el nivel de significación 0,05.
Como p = 0,000 < 0,05 se rechaza la hipótesis nula, por lo tanto, se puede afirmar que hay diferencias entre los resultados al inicio y al final en cuanto al desarrollo de habilidades, lo que se ha venido evidenciando descriptivamente: los resultados finales son mejores que los iniciales.
CONCLUSIONES
La solución de problemas matemáticos contribuye al desarrollo de la creatividad, la perseverancia y la adquisición y fijación de los conocimientos matemáticos, por tanto, la referida solución de problemas debería constituir el eje central de trabajo de la Matemática en el preuniversitario.
La tipología de los problemas propuestos en esta investigación contribuye al desarrollo de la competencia matemática de los estudiantes, constituye un importante complemento del libro de texto y está encaminada a desarrollar el proceso de enseñanza aprendizaje de las funciones exponenciales y logarítmicas al seguir una metodología de solución de problemas.
Acorde con lo planteado en el proceso de perfeccionamiento del sistema educativo, la tipología de problemas propuestos hace evidente las aplicaciones que tienen las funciones exponenciales y logarítmicas en diferentes esferas de la vida