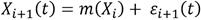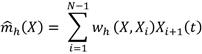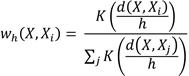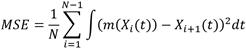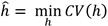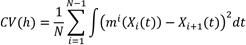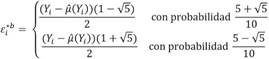Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El estudio del comportamiento de las variables meteorológicas ha sido un tema de significativa importancia a lo largo de la historia debido a que son netamente aleatorias por muchos factores. Desde hace mucho tiempo se han ajustado modelos de regresión de series de tiempo con buenos resultados, sobre todo para predecir valores a mediano plazo, y cuando se trata de ampliar este tiempo las predicciones se alejan de la realidad 21,22,23. En esta investigación se desarrolló una aplicación de un modelo no paramétrico funcional de series de tiempo funcionales que tiene un buen ajuste de la variable meteorológica de velocidad del viento y propone predicciones no a corto tiempo, debido a que predice uno o más datos funcionales (curvas) correspondientes a series de tiempo de velocidades del viento. El modelo antes mencionado tiene una forma no paramétrica adaptada a datos funcionales, como se detallará más adelante 5,24,25.
Modelo no paramétrico de series de tiempo funcionales.
Uno de los métodos más utilizados en las series de tiempo es el modelo de regresión no paramétrico. El modelo no paramétrico puede extenderse a las series de tiempo funcionales de la siguiente manera 14), (15), (16), (17), (18), (20.
()1
donde:
Xi(t) es el i-ésimo dato funcional en el instante t, con t que varía en un intervalo de tiempo. La Ecuación (1), representa una serie de tiempo para cada instante t que se ajusta con un modelo no paramétrico, más un término de error,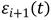 
.
El presente trabajo de investigación utilizó el estimador de Nadaraya-Watson de m(X), basado en las ideas de Aneiros-Perez et al. (2011), presentes en la Ecuación (2),
()2
donde el parámetro h es la ventana de suavizado, N es el tamaño de la muestra, y,
()3
En la Ecuación (3), K es una función tipo núcleo y d es una distancia que puede ser una métrica o la semimétric.pca 9,26.
En este estudio, K es el núcleo Gaussiano, la distancia d es la semimetrica que calcula la distancia entre curvas según el método de análisis de componentes principales funcionales, además el presente trabajo se consideró en el espacio L2 de funciones módulo al cuadrado integrables (1), (4), (5), (6).
Para el ajuste del modelo se minimizó el error cuadrático medio de la Ecuación (4), usando una ventana estimada ĥ de suavizado obtenida mediante validación cruzada (CV) en la ecuación (5).
()4
()5
donde,
()6
siendo:
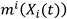(7) el estimador de Nadaraya- Watson estimado con todos los datos salvo la observación i-ésima.
MATERIALES Y MÉTODOS
Metodología.
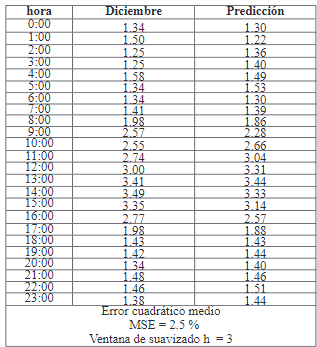
La investigación se centró en la aplicación del modelo no paramétrico de series de tiempo funcionales de la ecuación (1), a la variable meteorológica velocidad del viento, que contiene velocidades en cada hora de los días del año 2019. Una vez ajustado el modelo con las velocidades en los meses desde enero a noviembre, y a la vez se consideró a diciembre como mes testigo, posteriormente se establecieron las 24 predicciones y luego se compararon con las velocidades reales del mes de diciembre, obteniendo un error cuadrático medio menor al 3%.
Muestra
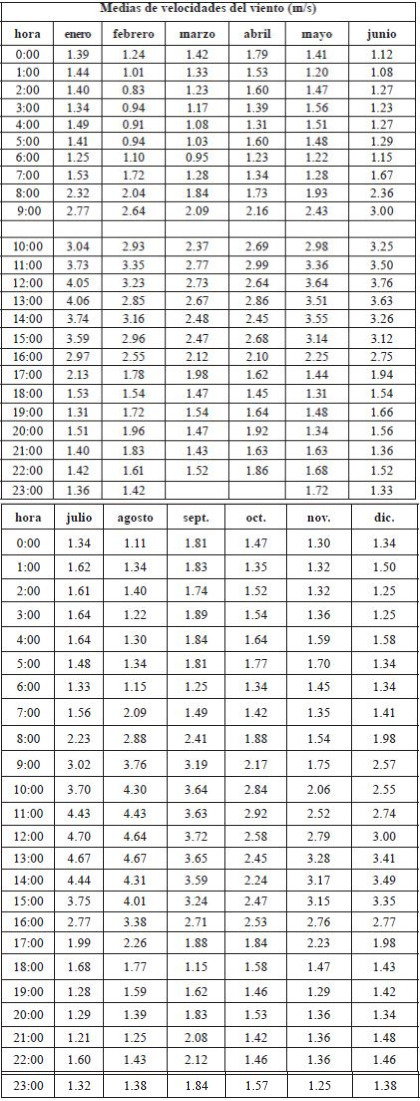
La muestra de tamaño 8760 corresponde a las velocidades del viento en metro por segundo de cada hora en los meses del año 2019, descargadas de la estación meteorológica de la Escuela Superior Politécnica de Chimborazo, ubicada en la Parroquia San Juan a una altitud de 4350 msnm en el kilómetro 30 vía Calpi - Guaranda en la provincia de Chimborazo - Ecuador.
Procesamiento de la información
Los datos de la variable de las velocidades del viento se procesaron mediante la utilización del software estadístico R 9,10,11,12,13, los cálculos de las medias de las velocidades por cada hora del día y en cada mes del año 2019 se convirtieron en una variable funcional con valores que determinaron 12 curvas con 24 datos cada una, (correspondientes a las horas), para los meses de enero a diciembre.
Preparación del código
Se realizó la programación de un script con una codificación destinada a establecer el modelo no paramétrico de series de tiempo funcionales, tomando en cuenta el lenguaje de código correspondiente y la teoría estadística inherente a este tipo de modelo 2), (3), (7), (8.
Ajuste del modelo
El modelo no paramétrico, se ajustó a los datos funcionales de medias de velocidades del viento por cada hora de los meses de enero a noviembre. Con este modelo ajustado se realizaron las predicciones de 24 valores, mismos que se compararon con los valores reales de las medias de las velocidades del viento del mes de diciembre.
Con los datos procesados se obtuvieron 2 gráficas: Gráfica de la serie de tiempo de las medias de las velocidades del viento de los meses, de enero a diciembre, junto con las 24 predicciones del modelo no paramétrico funcional.
Gráfica de la serie de tiempo de las medias de las velocidades del viento del mes de diciembre, junto con las 24 predicciones del modelo no paramétrico funcional.
Adicionalmente, se procedió al calculó el error cuadrático medio, MSE, para medir el porcentaje de error entre las predicciones del modelo con los valores correspondientes al mes testigo (diciembre), lo que permitió obtener una nueva gráfica de las medias de las velocidades del viento de diciembre con intervalos de confianza wild bootstrap al 95%, junto a las predicciones del modelo no paramétrico.
RESULTADOS
Los resultados se presentan en tablas y gráficas, que detallan la información de la variable funcional con valores de medias de las velocidades del viento de cada mes, y además, contienen las predicciones del modelo junto con los valores del mes testigo y el valor calculado del error cuadrático medio en porcentaje.
En la Tabla 1 se observan los valores de las medias de las velocidades del viento por cada hora en cada mes del año 2019, calculados con el software R.
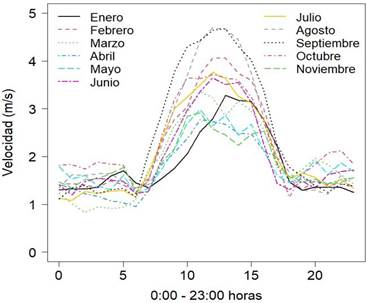
Figura 1 Serie de tiempo funcional de medias de las velocidades del viento de los meses de enero a noviembre de 2019.
La serie de tiempo funcional de la Figura 1, de 11 curvas de medias de velocidades de viento pertenecen al espacio L² de funciones módulo al cuadrado integrables sobre el intervalo de tiempo de 0 a 24 horas, condición necesaria y suficiente para realizar el ajuste del modelo no paramétrico funcional.
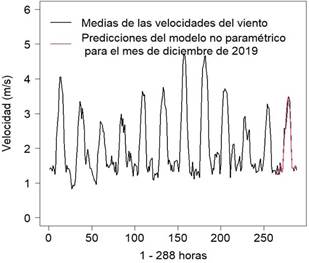
En la Figura 2, se presentan las medias de las velocidades del viento versus las 288 horas correspondientes a los meses de enero a diciembre del año 2019, donde a cada mes corresponde 24 horas (ver Tabla 1). Además, se muestran las predicciones del modelo no paramétrico funcional (curva de color rojo), junto a la curva correspondiente al mes de diciembre (curva de color negro).
DISCUSIÓN
Los 24 pares ordenados con las horas desde 0:00 a 23:00, y los valores de las medias de las velocidades del viento que corresponden a cada mes, constituyen un dato de la serie de tiempo funcional de la velocidad del viento. En total se tienen 12 datos funcionales correspondientes a los meses del año 2019.
Por consiguiente, al unir estos 12 datos funcionales (curvas) uno a continuación de otro se obtiene una serie de tiempo que contiene 288 pares ordenados, como se observa la curva en la Figura 2.
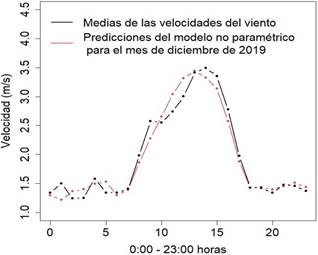
Figura 3 Medias de las velocidades del viento de diciembre junto a las predicciones del modelo no paramétrico.
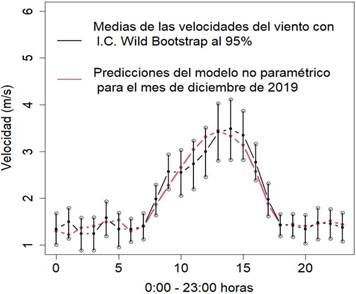
Figura 4 Medias de las velocidades del viento de diciembre con intervalos de confianza wild bootstrap al 95%, junto a las predicciones del modelo no paramétrico (19).
Los intervalos de confianza wild boostrap son generados mediante las b réplicas:
()8
Donde,
()9
Yi en cada hora i del día, es un vector de valores de las velocidades del viento de los días de diciembre.
en cada hora i del día, es la media de las velocidades del viento.
CONCLUSIONES
Los modelos estadísticos de regresión no paramétricos funcionales de series de tiempo funcionales tienen amplia aplicación en la actualidad. La predicción de la serie de tiempo de las medias de velocidades del viento correspondientes a un mes, y a cada hora de las 24 del día, hace notar la gran potencia de ajuste y predicción de este tipo de modelo en esta variable climática a diferencia de los comúnmente utilizados.
En esta investigación, tras el estudio realizado de modelos no paramétricos funcionales de series de tiempo funcionales, se evidenció que los datos funcionales correspondientes a las medias de las velocidades del viento en cada hora del año 2019 cumplen las condiciones necesarias para la correcta aplicación de este tipo de modelos.
El buen ajuste del modelo antes mencionado, de las medias de velocidades del viento en cada hora de los meses de enero a noviembre de 2019, evidenció que, con su predicción correspondiente a un mes, y la serie de velocidades del viento del mes testigo, diciembre, permitió obtener un excelente acercamiento al observar que cada una de dichas predicciones se encontraban dentro de los intervalos puntuales de confianza wild bootstrap al 95% de dicha serie del mes testigo, y además de muy buena precisión con el error cuadrático medio menor al 3%.
Además, con esta investigación se abre la posibilidad de realizar predicciones de series de tiempo utilizando datos funcionales (curvas), de otras variables meteorológicas en la zona centro de Ecuador.
