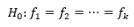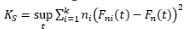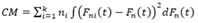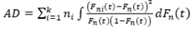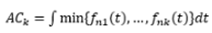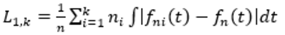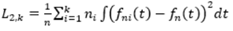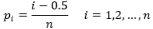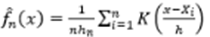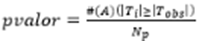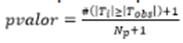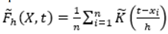Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El análisis de la distribución del ingreso personal permite visualizar los cambios en la misma a lo largo del tiempo. En la presente investigación se analiza lo sucedido con la distribución del ingreso personal del país, de las provincias, considerando que se aprecia un desarrollo desigual a este nivel. Además, es importante conocer qué ha sucedido a nivel de las actividades económicas dada la segmentación del mercado laboral en actividades de alta y baja productividad1, lo que se traduce en desigualdades de ingresos en los hogares.
Sea N el número de unidades de análisis (hogares o personas) y sean los ingresos x_1,x_2,...,x_N donde x_1<x_2<...<x_N de cada unidad de análisis, respectivamente. Una forma de representar la distribución del ingreso es la función de densidad de frecuencias f(x). Para cualquier nivel de ingresos x, f(x) dx es la proporción de receptores de ingresos cuyos ingresos se encuentran en el rango [x, x+dx], f(x) es independiente de la can tidad de unidades perceptoras de ingresos, o tamaño poblacional (N) y, por otro lado, es análoga a una función de densidad de probabilidad.
Para modelizar la distribución del ingreso, las formas funcionales dependen de las propiedades que se supone deben cumplir. En Dagum 1 se encuentra una lista de once propiedades que guían la selección del modelo entre las que se encuentran: interpretación económica de los parámetros, parsimonia, buen ajuste a lo largo de todos los niveles de ingresos, entre otros.
Hasta los años setenta los modelos más utilizados fueron el de Pareto y el Lognormal, que satisfacen pocas de las propiedades descritas anteriormente y que son deseables. La distribución de Pareto de acuerdo con su bondad de ajuste, simplicidad funcional y la interpretación económica de sus parámetros, continúa siendo considerada para la distribución de los grupos de ingresos muy altos, mientras que la Lognormal se ajusta a toda la distribución del ingreso, pero es bastante pobre en describir las colas de la distribución. Luego estos modelos fueron superados por aquellas distribuciones que toman en cuenta la propiedad de parsimonia 1,2. Con el tiempo, con el fin de tener en cuenta varias regularidades empíricas observadas y debido al aumento de la capacidad computacional, se han desarrollado y adoptado modelos estadísticos más generales.
Una forma alternativa de obtener estimadores de la densidad de los ingresos es mediante métodos no paramétricos. La gran ventaja es que en el enfoque no paramétrico se libera de las especificaciones paramétricas y se permite que los datos hablen por sí mismos. Se imponen supuestos mínimos sobre los datos, como que la densidad de ingresos debe existir y se debe satisfacer algunas propiedades de suavizamiento.
De acuerdo con Pittau 3, un enfoque no paramétrico basado en la estimación de la densidad de núcleo tiene mejores resultados, además se pueden capturar incrementos absolutos en los niveles de ingresos a la derecha o izquierda por medio de cambios en la función de densidad. Este método provee una imagen completa de la distribución de ingresos en términos de la función de densidad de frecuencia del ingreso, con la que se puede observar el nivel de distribución, modalidad y extensión, simultáneamente 4.
Para establecer si ha habido cambios estadísticamente significativos en la distribución del ingreso personal en el presente trabajo se aplican contrastes no paramétricos de bondad de ajuste para medir la igualdad de k distribuciones. Los que se utilizan basados en la función de distribución empírica (FDE) son las generalizaciones de las pruebas de Kolmogorov - Smirnov (KS) y Anderson, Darling (AD) discutidos en Kiefer 5.
Además, bajo el supuesto de que las distribuciones son totalmente continuas se presentan cuatro estadísticos basados en la comparación de la función de densidad núcleo (KDE). Los principales supuestos para la construcción de estos estadísticos, son que las k muestras observadas en realidad se generaron de la misma función de densidad; y que, para cada muestra es posible tener una KDE. Por lo que se podría diseñar y utilizar diferentes medidas de similitud para cuantificar las semejanzas entre los k diferentes KDE. Estas medidas son: AC o área común, Norma L1, Distancia L2 o Euclidiana y Distancia Sk. Esta clase de pruebas son prácticamente nuevas y recientemente investigadas. Los resultados obtenidos 6, a partir de simulación sugieren que las pruebas basadas en KDE son más potentes cuando las po blaciones subyacentes difieren en su forma.
En este contexto y tomando en cuenta que en muchos casos la función de densidad proporciona una información más intuitiva y directa que la función de distribución, además que la estimación de densidades proporciona métodos para abordar otros problemas como la discriminación, simulación, estimación de la moda, entre otros, el presente trabajo de investigación es un aporte ya que propicia el uso de otros estadísticos para pruebas de k poblaciones basados en la función de densidad (KDE) en especial en variables como el ingreso que presentan asimetría en su distribución. A partir de los resultados obtenidos se tendrán criterios para identificar el desempeño de las pruebas aplicadas para k muestras.
En la Sección 2 se desarrolla los aspectos más importantes del marco teórico tanto los relacionados con la distribución del ingreso como los estadísticos utilizados para probar la igualdad entre k muestras. También se describe la fuente de información, la base de datos y el proceso de tratamiento de los datos utilizados para este trabajo; de igual manera se describe la metodología empleada y la aplicación de las pruebas de hipótesis para k muestras basadas en la función de distribución empírica (FDE) y la función de densidad (KDE). Finalmente, se hace la validación de los resultados a partir del análisis de los estudios de simulación realizados por los autores que han aplicado estas pruebas.
En la Sección 3 se exponen los resultados obtenidos. En un primer momento, se realiza el análisis gráfico de la distribución de los ingresos personales tanto a nivel nacional como territorial y por actividad económica, para estudiar si estas siguen una distribución normal por lo que se aplican varias pruebas que permitan conocer si se rechaza o acepta la hipótesis de normalidad de las distribuciones de los ingresos. A continuación, se realiza un análisis gráfico de las funciones de densidad de los ingresos, y en un tercer momento, se presentan los resultados de la aplicación de los estadísticos propuestos con su nivel de significancia en cada caso y por cada método.
Finalmente, en la Sección 4 se incluyen las conclusiones derivadas del desarrollo del presente trabajo, enfocándose en hallazgos encontrados en cuanto a las diferencias en la distribución de los ingresos y en los resultados sobre la aplicación de las pruebas basadas en KDE y FDE, que indican que las basadas en la FDE son mejores cuando las distribuciones presentan cambios en la localización más que en la forma, como sucede en algunas de las desagregaciones analizadas.
MATERIALES Y MÉTODOS
La literatura distributiva utiliza el término distribución del ingreso “para hacer referencia a la lista completa de ingresos en una comunidad y no a alguna medida de disparidad de esos valores entre las personas” 7.
En el presente trabajo la discusión está enmarcada en el análisis de la función de distribución empírica del ingreso2, se hace referencia a aquel recibido de manera personal por un individuo en su mayoría, una persona con empleo; por lo que no se hacen ajustes para obtener un ingreso per cápita familiar u otra medida que dé cuenta de ajustes por factores demográficos o arreglos intrahogar.
El uso del enfoque paramétrico para el análisis distributivo se aplica ampliamente en la literatura estadística ya que algunas formas funcionales son idóneas para modelar algunas características de muchas distribuciones empíricas de los ingresos 8.
Como se señaló anteriormente existe la posibilidad de no predeterminar ningún modelo para la distribución de probabilidad de la variable y dejar que la función de densidad pueda adoptar cualquier forma. A este enfoque se lo denomina estimación no paramétrica de la densidad y tiene entre sus orígenes los trabajos de Fix y Hodges 9.
Varios han sido los autores que han utilizado este enfoque para analizar la distribución del ingreso 10. Burkhauser, Crews, Daly y Jenkins 11, utilizaron la estimación de densidad de núcleo / kernel para examinar los cambios en la distribución de los ingresos de los hogares de Estados Unidos en los años 80. Liu y Zou 12 estudian la creciente desigualdad de ingresos en China en las últimas tres décadas con énfasis en la migración urbana-rural, el progreso económico y tecnológico. Nenovsky y Tochkov 13 examinan el proceso de convergencia entre Europa Central y Oriental (CEE) y la Unión Europea (UE) durante todo el período de transición. Para ello se construyen las distribuciones de densidad de núcleo /kernel y analizan la evolución de su forma para determinar tendencias de convergencia.
Estadísticos basados en la Función de Distribución Empírica (FDE)
Con estas pruebas se realiza la comparación entre Fn(X) (la FDE) y F(X) la función de distribución acumulada (FDA) para ver si coinciden.
Esto lleva al desarrollo de los estadísticos basados en FDE que utilizan las diferencias entre Fn(x) y F(x) para determinar si la muestra proviene de F(x).
Cuando se analizan varias muestras, es de interés conocer si proceden de la misma población. Se supone que se tiene ni observaciones generadas de una función de densidad de probabilidad k, fi,i=1,2,...,k, y el interés es probar la hipótesis nula.
()1
Distancia de Kolmogorov-Smirnov
()2
Para t Є ℝ, y donde Fn es la función de distribución empírica que corresponde a la muestra conjunta y Fnt es la función de distribución empírica acumulada relacionada con la i-ésima muestra.
Cramér-Von Mises: La generalización de este estadístico para el problema de comparación de k-muestras independientes fue propuesta por 5 y está definida como:
()3
Donde dadas k-muestras independientes de tamaños n1,...,nk, Fni (t), representa la FDE asociada a la i-ésima muestra (1≤i≤k) y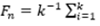 
7
Anderson-Darling: La prueba para k-muestras de Anderson-Darling es una prueba de rango y, por lo tanto, no hace las suposiciones restrictivas de los modelos paramétricos. Suponiendo que la i-ésima muestra tiene una función de distribución continua Fni y la finalidad es probar la hipótesis H0=F1= ... =Fk sin hacer especificaciones sobre la distribución conjunta F.
Se denota la función de distribución empírica de la i-ésima muestra como Fni (t) y la de la muestra agrupada de todas las N=n1+...+nk observaciones por Fn (t). El estadístico de la prueba Ander-son-Darling para k-muestras se define como:
()4
Estadísticos basados en la Función de Densidad de Núcleo (KDE)
Suponiendo que se quiere probar si k diferentes muestras observadas se generaron de la misma función de densidad de probabilidad subyacente, y suponiendo que, para cada muestra, es posible obtener una estimación de densidad de núcleo (Kernel), KDE. Intuitivamente, si todas las k-muestras han sido generadas desde la misma función de densidad de probabilidad, entonces los k diferentes KDE obtenidos deberían ser muy similares. Esto sugiere que uno podría diseñar y usar diferentes medidas de similitud para cuantificar las semejanzas entre los k diferentes KDE, en la forma de un único valor escalar, un estadístico.
Área Común, AC: Este nuevo concepto fue introducido por Martinez-Camblor 7, está definido cómo:
()5
Donde fni, es el estimador de la densidad de núcleo perteneciente a la i-ésima muestra. AC es el área común donde las k densidades se superponen. Si el valor es cercano a uno, las funciones de densidad de probabilidad son casi idénticas, y la hipótesis H0 nula que formula que f1=f2= ... =fk no puede ser rechazada. Por otro lado, un valor pequeño de AC significa que las muestras probablemente son generadas a partir de diferentes distribuciones.
Norma L1: Si se denota fni como el estimador de la densidad de núcleo, KDE, perteneciente a la i-ésima muestra de tamaño ni, i=(1,2,...,k), siendo k el número de muestras y fn la KDE de la muestra conjunta con n=n1+n2+...+nk. Así la generalización de la distancia L1 puede ser escrita de la siguiente manera:
()6
De acuerdo a la definición del Área Común, se puede observar que para el caso k=2, el área común puede ser considerada como una generalización de la distancia L1.
Distancia L2 o Euclidiana. De acuerdo a Baranzano 1;, se define como:
()7
Para fni,fn,ni y n definidos de la misma forma que para L1. Nótese que si se reemplaza f(∙) por F(∙), se obtiene esencialmente la generalización de las pruebas para k muestras de Cramér-von Mises.
()8
De acuerdo a esta expresión se puede ver la analogía con la distancia de Kolmogorov-Smirnov en este caso la diferencia está, que en el contraste con la distancia KS que utiliza la función de distribución empírica acumulada FDEA, el cálculo de la distancia S se basa en las KDE 14.De acuerdo a los objetivos planteados, se aplican estas pruebas para identificar los cambios en la distribución del ingreso en el país a nivel de provincia y actividad económica.
El procedimiento metodológico aplicado consiste en las siguientes fases: en un primer momento se realiza la descripción de las bases de datos a utilizar, luego se define la variable de interés, a continuación se realiza el análisis exploratorio de esta variable a partir de las bases de datos de las encuestas de empleo para el período 2006-2016, el siguiente paso consiste en la estimación de las funciones de densidad y de distribución para la aplicación de las pruebas propuestas, finalmente, se analizan e interpretan los resultados.
La principal fuente de información será el Instituto Nacional de Estadísticas y Censos -INEC-, entidad encargada de proveer la estadística oficial del país. Puntualmente se hará uso de los datos levantados en la Encuesta Nacional de Empleo, Desempleo y Subempleo ENEMDU. Uno de los propósitos de la encuesta es, conocer la actividad económica y las fuentes de ingresos de la población.
Para los fines de este trabajo el análisis se realizará en función del ingreso personal total, no solo refleja la capacidad de obtener ingresos de un individuo, sino que también mide su potencial sobre el bienestar 15.
Además, se adoptó la transformación logarítmica de los ingresos, con el fin de capturar adecuadamente la estructura subyacente de las densidades en el rango de ingresos más bajos 16.
Debido a que la forma de la distribución del ingreso es sensible a las fluctuaciones de los precios y que se realizarán comparaciones de los cambios reales en el ingreso promedio y en el movimiento de la distribución a través de los años, los ingresos utilizados han sido ajustados por el Índice de Precios al Consumidor (IPC)3 de diciembre de 2016. Ya que se realizará un análisis temporal entre el año 2006 y 2016, solo se tomaron en cuenta las provincias que tienen información para todos los años. En el caso de las provincias de la Amazonía de acuerdo al INEC, estas solo son representativas en la ENEMDU a partir del 2014 por lo que se dispone de tres años de análisis, por esta razón se ha agrupado a estas provincias en un solo dominio. Se analiza un total de 16 dominios.
Para el análisis de los ingresos por actividad económica se utilizará la Clasificación Industrial Internacional Uniforme de Actividades Económicas (CIIU Revisión 4.0) que sirve para clasificar uniformemente las actividades o unidades económicas de producción, dentro de un sector de la economía, según la actividad económica principal que desarrolle. Fue necesario efectuar una correlación de la “Clasificación Nacional de Actividades Económicas” (CIIU Rev. 4.0), con la versión anterior “Clasificación Nacional de las Actividades Económicas de acuerdo a la CIIU - Rev. 3.1”. De acuerdo a la clasificación CIIU Rev. 4 se cuenta con 22 actividades, sin embargo, por la baja participación en algunas de ellas se optó por realizar el análisis de la distribución del ingreso para 7 ramas de actividad que comprenden en promedio el 75% de las personas ocupadas.
Procedimiento para el análisis de la forma de la distribución del ingreso a partir de métodos no paramétricos.
Las representaciones gráficas, como histogramas, curvas de Lorenz, gráficos de probabilidad normal o Q-Q Plot Normal y desfiles de enanos de Pen, se han utilizado con frecuencia como herramientas alternativas o complementarias para resumir las distribuciones de ingresos. Estos gráficos no se centran simplemente en una característica específica de la distribución, como lo hacen las diversas medidas puntuales, sino que resumen varias características de la distribución completa.
En este marco, el gráfico de probabilidad normal nos permite comparar la distribución empírica de un conjunto de datos con la distribución Normal. Supongamos que disponemos de un con-junto de observaciones xi,(i=1,2,...,n).
Sea F(x) la función de distribución de una distribución especificada. El gráfico de probabilidad se construye de la siguiente manera:
1) Se ordena las observaciones de menor a mayor en la forma x(1)≤x(2)≤ ... ≤x(n)
2) Se determina los valores
()9
Si por Qx(p) notamos al cuantil de orden p(0<p<1) de las observaciones, tenemos que: xi=Qx(pi ) i=1,2,...,n
3)Determinar los cuantiles de orden pi,i=1,2,...,n de la distribución teórica representada por la función de distribución F, es decir:
Qt(pi )=F -1 (p i ) i=1,2,...,n
4) Representar el conjunto de puntos (Q t (p i ), Q x (p i )), i=1,2,...,n o ((F -1 )p i ,x i )
Si la distribución teórica constituye una buena aproximación de la distribución empírica, es de esperar que los cuantiles de los datos estén muy próximos a los de la distribución teórica y, por tanto, los puntos del gráfico estarán muy próximos a la bisectriz del primer cuadrante.
Por otra parte, la función de densidad de núcleo (Kernel) y sus gráficos correspondientes proporcionan una interpretación simple y directa de la distribución del ingreso. El mecanismo para el presente análisis será a través de la estimación de la densidad de núcleo.
Supongamos que queremos probar la igualdad de k poblaciones con densidades f_1,...,f_n, dadas k muestras aleatorias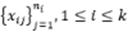 
, extraídas independientemente de sus respectivas densidades. El estimador de la densidad de núcleo está dado por:
()10
Donde K(x) es una función denominada función Núcleo, que cumple algunas condiciones de regularidad, generalmente es una función de densidad simétrica de media cero, {hn} es una secuencia de constantes positivas conocida como ancho de banda, parámetro de suavización o bandwith. Si h→∞, entonces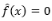 
para todo x.
El estimador de densidad de núcleo será obtenido a partir de la función density de R que tiene los siguientes argumentos:
density(x, bw = "nrd0", adjust = 1, kernel = c("-gaussian", "epanechnikov", "rectangular", "trian-gular", "biweight", "cosine", "optcosine"), weights = NULL, window = kernel, width, give.Rkern = FALSE, n = 512, from, to, cut = 3, na.rm = FAL-SE, ...)
Donde,
x son los datos a partir de los cuales se calculará la estimación,
bw, es el ancho de banda suavizado que será utilizado. El valor predeterminado, "nrd0", es 0.9 veces el mínimo de la desviación estándar y el rango intercuartil dividido por 1.34 veces el tamaño de la muestra a una potencia quinta negativa ('regla de oro' de Silverman) a menos que los cuartiles coincidan cuando se garantice un resultado positivo.
kernel, una cadena de caracteres que contiene la lista de núcleos que serán utilizados, tiene como predeterminado el núcleo gaussiano.
n, es el número de puntos igualmente espaciados en los que se debe estimar la densidad, si n>512, se redondea a una potencia de 2 durante los cálculos y el resultado es interpolado.
Para graficar la función de densidad de núcleo de los ingresos se utiliza la librería plotly y ggplot2 de R.
Procedimiento para la aplicación de las pruebas no paramétricas para k muestras
Se consideran las siguientes hipótesis nulas sobre la homogeneidad de k poblaciones (Xi,j): Basadas en la función de distribución:F1=F2=...Fk
Basadas en la función de densidad: f1=f2=...fk
Aplicación de la generalización de la prueba para k muestras de Kolmogorov - Smirnov (KS)
Para la implementación del algoritmo que permita obtener este estadístico se siguió lo desarrollado por Baranzano (14) en el que se aplica una prueba basada en permutaciones para probar la hipótesis nula H0 de igualdad de k poblaciones. Es importante indicar que en el trabajo mencionado solo se realiza una aplicación para tres muestras por lo que el algoritmo propuesto en este trabajo es un aporte al extender el procedimiento a k muestras.
El procedimiento se aplica de la siguiente manera:
Supongamos que se tienen dos muestras X y Y que pertenecen a la misma distribución y representan la hipótesis nula H0 siendo la hipótesis al ternativa que las muestras provienen de diferen tes distribuciones.
Denotamos KSkobs el estadístico observado y Tobs calculado de las muestras de datos simulados.
Los elementos de X y Y se juntan y permutan, luego de la permutación, los elementos se dividen en dos grupos X y Y, preservando el tamaño muestral original de estas muestras.
Luego el nuevo estadístico KSk=Tk es calculado de los datos permutados. Este procedimiento se re- pite 1000 veces, resultando en 1000 estadísticos
T1,…,T199, con lo que se construye la distribución del estadístico, conocida como distribución de permutación bajo la hipótesis nula.
El p valor se calcula como:
()11
Para 1≤i≤1000
Aquí #(A) representa el número de veces que el evento A se satisface y Np el número de permutaciones realizadas. Para incluir el estadístico observado se añade 1 al número total de cálculos, luego el pvalor se puede expresar como:
()12
Si el pvalor<α, la hipótesis nula H0 se rechaza, α representa el nivel de significancia, que es la cantidad de evidencia requerida para aceptar que es improbable que un evento haya surgido por casualidad (azar). En otras palabras, si es poco probable que se obtenga Tobs cuando se permuta (≤α), luego la hipótesis nula se rechaza. El valor seleccionado para α es 0.05.
Las variables de entrada para su aplicación son una lista que contiene la variable del logaritmo del ingreso personal total real por provincia y por año; así como una lista de la variable del logaritmo del ingreso personal total real por rama de actividad y por año. Para obtener el p valor se utilizaron 1,000 permutaciones, el desarrollo del código se encuentra en el Apéndice.
b)Aplicación de la generalización de la prueba para k muestras de Anderson Darling (AD)
Otra de las pruebas basadas en FDE es la genera lización para k muestras de la prueba de Ander son, Darling (AD) discutidos en (5).
Para la aplicación de esta prueba se utiliza el paquete kSamples desarrollado en R por Fritz Scholz y Angie Zhu en agosto de 20174. Este paquete tiene como objetivo comparar k muestras utilizando, entre otros, el estadístico de Anderson-Darling, así como el de Kruskal-Wallis con diferentes criterios de puntajes. Calcula p valores asintóticos y p valores exactos (simulados o limitados). Para obtener más detalles se puede acceder a la documentación del paquete disponible en el repositorio CRAN de R (17).
Aplicación de las pruebas basadas en la función de densidad - KDE
Las pruebas que serán desarrolladas en este trabajo son:
Generalización para k muestras de la norma L1
Generalización para k muestras de la norma L2
Generalización para k muestras de la distancia Sk
Generalización para k muestras del Área Común AC
El estadístico del Área Común es desarrollado por el método de permutaciones, siguiendo un procedimiento similar al detallado en el apartado anterior el código se encuentra en Apéndice.
Para la aplicación de las tres pruebas propuestas basadas en KDE, con los que se realiza el contraste de la hipótesis nula, se ha implementado un código en R siguiendo el trabajo desarrollado (4), en este trabajo solo se había implementado la función L1 para dos muestras, por lo que este trabajo aporta con el desarrollo del algoritmo de las generalizaciones para k muestras de las pruebas L1, L2, AC y Sk.
El código en R de las funciones se encuentra en el Apéndice.
Planteamiento Bootstrap
El estimador núcleo de la densidad fni (i=1,2,3) utiliza para el cálculo de los
estadísticos L1, L2 y Sk un ancho de ventana de la forma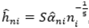 
donde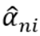 
, representa la desviación estándar en la i-ésima muestra y donde S varía en una determinada matriz de valores.
En todos los casos se utilizó el núcleo Gaussiano. En este contexto, en el que el supuesto es que las poblaciones de origen son continuas, el método con el que se obtiene mejores resultados para la aproximación del valor crítico de los estadísticos de prueba a un nivel α es el Bootstrap suavizado, que se basa en la generación de muestras desde la Función de Distribución Empírica Suavizada (FDES), dada una muestra aleatoria X=x1,...,xn, queda definida de la siguiente manera:
()13
Donde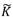 
es una función de distribución, usualmente elegida de modo que su derivada sea una función de densidad simétrica, de media cero y varianza finita; h=h(n) es una sucesión de números reales positivos, como parámetros ventana, que en general no son de la misma naturaleza que los utilizados en la estimación de núcleo para la función de densidad. Dadas k muestras aleatorias simples X=X1,...,Xk de tamaños n1,...,nk, respectivamente, se construye una región crítica para el contraste:
H0:fi=fj, j∈ 1,...,k;
H1=no se cumple H 0
Asumiendo que la hipótesis nula es cierta, y si las muestras son independientes, es razonable plantear el siguiente plan de remuestreo:
Desde la muestra conjunta X, se calcula la FDES definida en (60) y se calcula el estadístico F(X).
Aleatoriamente, se generan B remuestras Bootstrap (Xb) de tamaño n i (i=1,...,n) de la distribución calculada en el paso anterior. Para cada muestra Bootstrap se calcula el valor del estadístico F(Xb).
Se aproxima la distribución del estadístico F(X) a partir de los valores F(Xb) y se toma el 1-α percentil a lo largo de las remuestras Bootstrap como el valor crítico.
Las variables de entrada son: Una lista que contiene la variable del logaritmo del ingreso personal total real por provincia y por año; así como una lista de la variable del logaritmo del ingreso personal total real por rama de actividad y por año. Para la aplicación de estas pruebas se utilizaron 500 remuestras en la función de Bootstrap. En el Apéndice se encuentra el código desarrollado en R.
RESULTADOS
En América Latina la desigualdad de la distribución del ingreso se ha reducido desde principios de la década de 2000, gracias a un aumento más rápido de los ingresos en los quintiles más bajos que en el resto de la población. No obstante, el ritmo de reducción de la desigualdad se ha desacelerado y, de acuerdo con fuentes complementarias a las encuestas de hogares, no ha disminuido e incluso puede haber aumentado la participación de los grupos más ricos en el total de los ingresos 18.
Al analizar las cifras de pobreza por ingresos en el Ecuador para el período 2006-20165, a nivel nacional se encuentra que la incidencia de la pobreza extrema se redujo a la mitad en el período analizado y la incidencia de la pobreza se redujo en alrededor de 15 puntos porcentuales (19.
Esta tendencia de reducción se mantiene en este período para las provincias de la Sierra y la Costa. Sin embargo, las provincias de la Amazonía muestran un panorama diferente. Analizada como un solo dominio, entre 2006 y 2016 la Amazonía mantuvo constante su incidencia de pobreza extrema. Y más aún, en 2016 las provincias de Morona Santiago, Napo y Pastaza tuvieron tasas de pobreza extrema superiores al 30%.
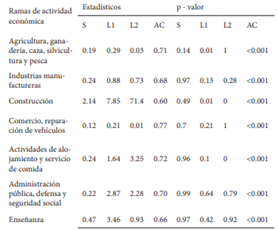
En cuanto a las ramas de actividad económica se aprecia que la Agricultura, ganadería, silvicultura y pesca es la que concentra la mayor cantidad de personas en situación de pobreza, a 2016 el 46% de la población ocupada en estas actividades es pobre.
En el período analizado todas las ramas de actividad han reducido la tasa. Siendo las que más la Agricultura y la Construcción con reducciones de 14 y 12 puntos porcentuales. Las que menos la Administración pública, defensa y seguridad social y Enseñanza que para 2016 prácticamente no registran población pobre por ingresos.
Los últimos veinticinco años, 1990-2014, muestran varios hechos que marcan la trayectoria de la economía ecuatoriana. Se pueden distinguir tres períodos de análisis: 1990-1999, 2000-2006, y 2007-2014 20.
El PIB de Ecuador, en el cuarto trimestre de 2016, a precios constantes, mostró una tasa de variación anual (t/t-4, respecto al cuarto trimestre de 2015) de -1.2%. Desde 2005, las tasas de crecimiento del PIB en Ecuador han sido altas, con excepción de 2009, 2015 y 2016. De acuerdo a las cifras del precio real del petróleo y los términos de intercambio, estos son precisamente los años en que las condiciones externas se volvieron desfavorables para Ecuador. De hecho, para el período 2005-2015, la correlación entre el crecimiento del precio real del petróleo y el crecimiento del PIB ha sido de 0,74 20. Durante este período, como ya se revisó, la pobreza y la desigualdad disminuyeron significativamente.
Análisis de la Normalidad de las Distribuciones del Ingreso en el Período 2006-2016
Se realiza el contraste de las siguientes hipótesis:
H0= La distribución de los ingresos personales proviene de una normal entre los años 2006 a 2016
H1= La distribución de los ingresos personales no proviene de una distribución normal entre los años 2006 a 2016
En primer lugar, se realiza un análisis a partir de gráficos de probabilidad normal o Q-Q Plot Normal
A continuación, para ilustrar este análisis solo se presentan los gráficos a nivel nacional, de las ramas de actividad Agricultura, ganadería, caza, silvicultura y pesca y Enseñanza y de las provincias de Chimborazo, Azuay y El Oro.
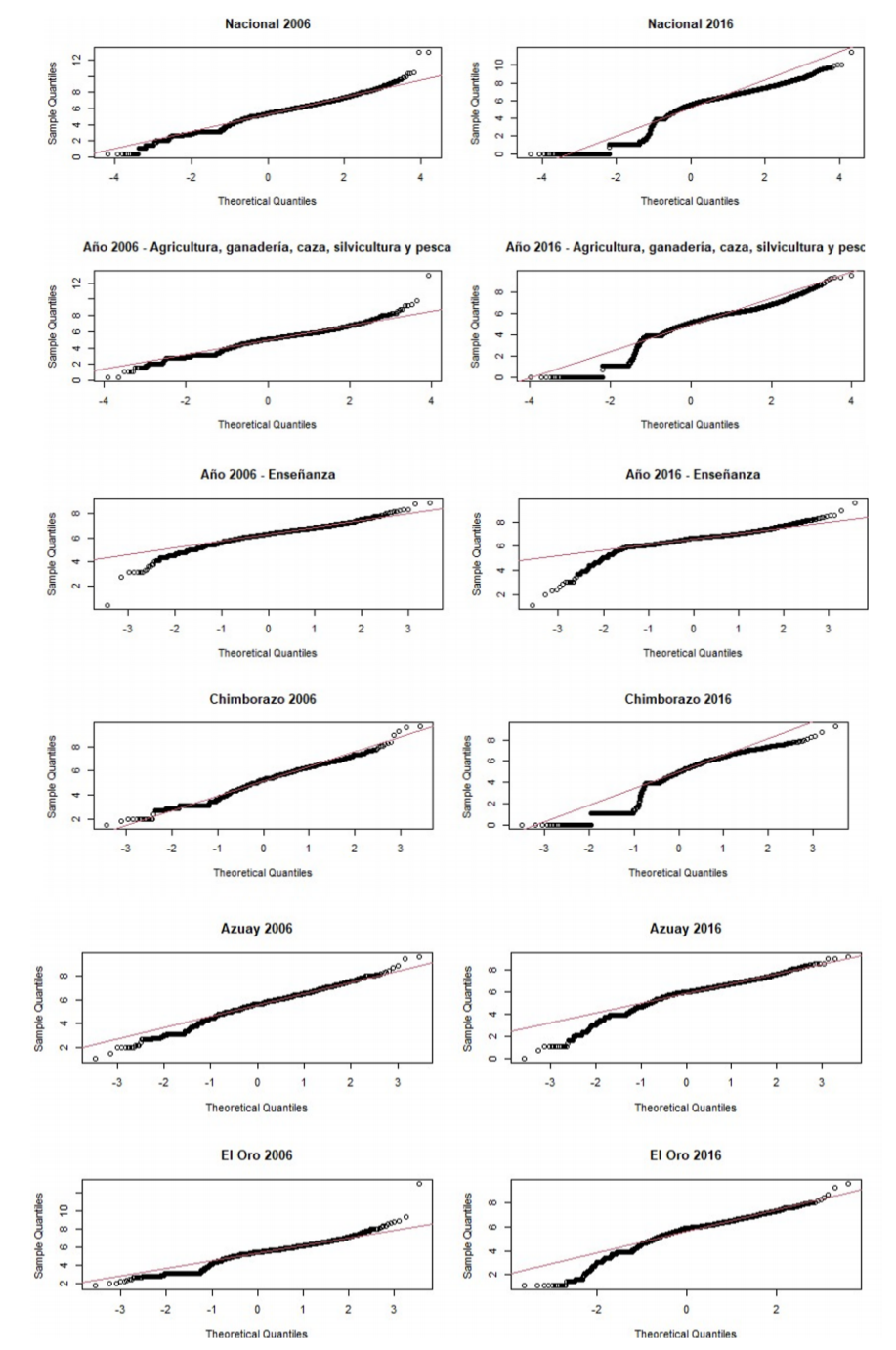
Figura 1 Gráfico de probabilidad normal o Q-Q Plot Normal de los ingresos totales personales reales período 2006-2016
Para inferir que la distribución de los ingresos personales en cada una de las desagregaciones proviene de una Normal las curvas deberían ajustarse a la línea roja, es decir que el valor del cuantil de la muestra coincide con el valor exacto del cuantil teórico correspondiente.
Sin embargo, de acuerdo a los resultados obtenidos, en la Figura 1 se puede apreciar que en todos los casos los datos no se distribuyen simétricamente y muestran un sesgo a la izquierda, con colas pesadas a la izquierda y en menor medida a la derecha. También, se observa que estas carac terísticas en la mayoría de los casos se acentúan en el 2016. Estas características dan indicios de la desigualdad de la distribución de los ingresos ya que las curvas no se asemejan a una curva Normal.
Para confirmar o rechazar la hipótesis nula de normalidad de los ingresos se aplican dos pruebas:
Prueba de Lilliefors (Kolmogorov-Smirnov) es una prueba ómnibus basada en la FDA para la hipótesis compuesta de normalidad. El estadísti co de la prueba es la máxima diferencia absoluta entre la función de distribución acumulativa em- pírica y la hipotética.
Puede calcularse como D=max{D+,D-}, para su aplicación se utiliza el paquete “nortest” de R 21.
Prueba de Jarque Bera, l procedimiento de esta prueba es bastante diferente al de las pruebas Kolmogorov-Smirnov y Shapiro-Wilk, esta prue ba se centra en la asimetría y la curtosis de los datos de la muestra y compara si coinciden con la asimetría y la curtosis de la distribución normal. Su aplicación se realiza con el paquete “nor mtest” de R 22.
Es importante indicar que se aplican estas pruebas como alternativa a las ya descritas en este estudio como son las pruebas de Kolmogorov-Smirnov, Anderson Darling y Cramer Von Mises.
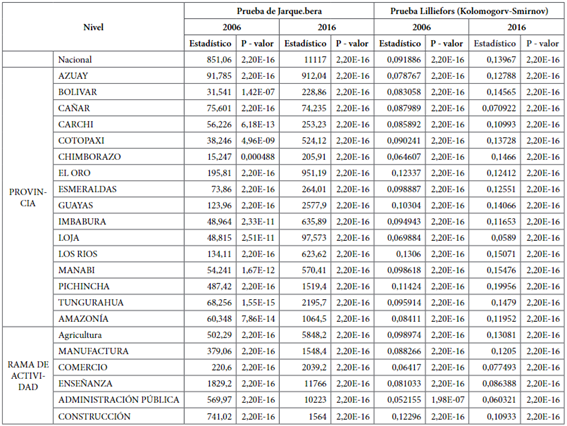
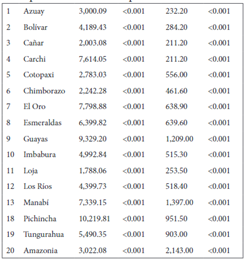
Se obtiene los siguientes resultados:
Los resultados obtenidos en la Tabla 1 muestran que en todos los casos no se puede aceptar la hipótesis nula y por el contrario se acepta la hipótesis alternativa que indica que la distribución de ingresos no sigue una Normal y por tanto se justifica el enfoque no paramétrico para medir los cambios en la distribución de los ingresos a través del tiempo y por distintos segmentos de la población
Análisis de la Homogeneidad de las Distribuciones del Ingreso en el Período 2006-2016
Se contrastó las siguientes hipótesis:
H 0 = No existen cambios en la distribución de los ingresos personales (función de densidad) entre los años 2006 a 2016
H 1 = Existen cambios en la distribución de los ingresos personales (función de densidad) entre los años 2006 a 2016
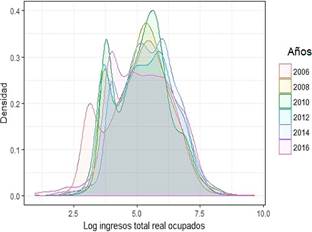
En primer lugar, se realiza un análisis gráfico de las funciones de densidad de los ingresos personales totales reales para el período de estudio.
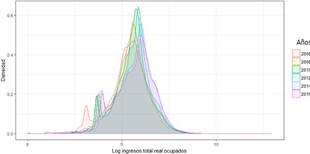
La Figura 2 de la función de densidad de núcleo para la distribución de los ingresos totales por año muestra en general la concentración de la población en cada nivel de ingresos, particularmente se aprecia:
Los cambios en la forma y localización de la distribución (respecto a la media o mediana) entre 2006 y 2016 con un movimiento hacia la de recha y aplastamiento de la función de densidad tiene implicancias en términos de crecimiento y desigualdad. El movimiento hacia la derecha es reflejo de un aumento del ingreso medio de la población, el aplastamiento de la función de densidad para 2016, sugiere un incremento de la desigualdad.
Un desplazamiento de la distribución de los ingresos a la derecha, el promedio de los ingresos entre 2006 a 2016 se incrementó en un 14%. Sin embargo, entre 2015 y 2016 el ingreso real decrece en un 4.82% (de una media de 531 a 506 dólares). Por su parte el salario básico unificado pasó de 160 a 366 dólares es decir se incrementó alrededor del 44%. Además, un traslado de las densidades hacia la derecha, explican la reducción de la pobreza, que para el caso del país en el período analizado se redujo en 15 puntos porcentuales 23.
La forma de la distribución tiene la característica de mostrar un grupo con una alta concentración alrededor de los valores de la moda y la media, lo que indicaría una menor desigualdad. Lo que también se refleja en las medidas puntua les del coeficiente de Gini, que ha permanecido estable en los últimos años (a partir de 2011). Se verifica que la desigualdad de ingresos ha dismi nuido a nivel nacional en el período analizado 2007-2015 24.
Se puede diferenciar tres períodos, el primero que es el salto de la distribución del 2006 al 2009, luego entre 2010-2012 se mantiene estable, alcanzando el mayor pico en 2012, para luego disminuir el nivel de la densidad, esto implica una movilización en la distribución que si bien sigue concentrada alrededor de la moda, es más dispersa respecto al año 2010 o 2012, por tanto el tercer período se aprecia entre 2013-2016, al mirar la gráfica parecería que esta dispersión fue hacia los niveles de menores ingresos, donde hay un mayor ensanchamiento de la curva. Esto podría estar relacionado con el aumento de la tasa de empleo inadecuado (de acuerdo al INEC pasa de 46.7% en 2014 a 53.4% en 2016).
Al revisar otras medidas puntuales del ingreso como la variación porcentual de los ingresos por cuantil 25. Al comparar cada año respecto al 2006 que es el año base para el análisis, se comprueba que hay una mejora en el nivel de los ingresos en general, pero sobre todo para los primeros 10 cuantiles. Por otro lado, al analizar la variación entre 2016 y 2014 se evidencia un decrecimiento de la media de los ingresos, sobre todo en primeros ocho cuartiles, mientras que los cuartiles con mayores ingresos permanecen prácticamente igual. Lo que también confirmaría la disminución de la densidad para 2016. Esto podría indicar una pérdida en el bienestar. Estos resultados en particular son consistentes con lo reportado por la CEPAL 26, en el que se indica que en hasta 2014 el incremento de los quintiles más pobres fue mayor que el de los quintiles más ricos, en tanto que para 2016 el ritmo de reducción de la desigualdad se ha desacelerado.
Resaltan dos protuberancias, la que se encuentra alrededor de la media y la mediana en cada año, que concentra la mayor cantidad de personas y una pequeña protuberancia que se encuentra en el intervalo 3.1,3.3; para 2006, 3.5,3.75; para 2008-2010, y 3.6,4,1; en 2015-2016, que corresponden a valores de USD 15 a USD 30, USD 35 y USD 50, respectivamente, lo que concuerda con los valores pagados por concepto de Bono de Desarrollo Humano, BDH en esos años; el grupo poblacional que se encuentra en esta agrupación está compuesta en su mayoría por mujeres, también predomina el empleo en la categoría de otro empleo no pleno y trabajo no remunerado (categoría que de acuerdo al INEC también forma parte de la población con empleo) y en vista que se analiza el ingreso total, se incluye también otras transferencias.
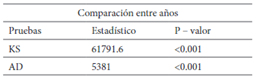
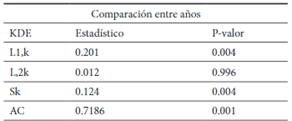
En cuanto al análisis de los estadísticos para pro bar la hipótesis nula, se obtuvieron los siguientes resultados:
De acuerdo a esto se rechaza la hipótesis nula de igualdad de la distribución de los ingresos en el período 2006 - 2016. A excepción de la norma L2 con la que se obtuvo un p valor de 0.99.
Análisis de la Homogeneidad de las Distribu ciones del Ingreso en el Período 2006-2016 por Provincia.
Se contrastó las siguientes hipótesis:
H 0 =No existen cambios en la distribución de los ingresos de la provincia i entre los años 2006 a 2016
H 1 = Existen cambios en la distribución de los in gresos de la provincia i entre los años 2006 a 2016
Donde i representa cada una de las provincias analizadas siendo: Azuay (1), Bolívar (2), Cañar (3), Carchi (4), Cotopaxi (5), Chimborazo (6), El Oro (7), Esmeraldas (8), Guayas (9), Imbabura (10), Loja (11), Los Ríos (12), Manabí (13), Pi- chincha (17), Tungurahua (18) y la Amazonía (30).
Para realizar un análisis gráfico más detallado se dividieron las provincias en dos grupos:
1: Azuay (1), Bolívar (2), Cañar (3), Carchi (4), Cotopaxi (5), Chimborazo (6), El Oro (7) y Esmeraldas (8).
2: Guayas (9), Imbabura (10), Loja (11), Los Ríos (12), Manabí (13), Pichincha (17), Tungurahua y Amazonía (30).
Respecto a la primera agrupación se puede decir que se aprecia la conformación de tres grupos. En el primer grupo de provincias se destacan El Oro y Azuay por ser las provincias que más concentración alrededor de la media presentan por tanto son las menos desiguales y con los ingresos más altos respecto al resto de provincias del grupo (una media de USD 500), el siguiente grupo lo conforman: Cañar, Esmeraldas, Carchi y Cotopaxi, que estarían un nivel medio, con ingresos más bajos, ya que las curvas se desplazan a la izquierda respecto al grupo anterior, finalmente se tiene a las provincias de Bolívar y Chimborazo que son las provincias que presentan mayor desigualdad e ingresos más bajos, el promedio de ingresos de Chimborazo para 2016 fue de USD 342 mientras que los de Azuay fueron de USD 511. En el gráfico a nivel de provincias, como en el nivel nacional también se observa una segunda protuberancia, en la que sobresale la provincia de Chimborazo, como se aprecia en la gráfica entre las provincias comparadas es la que mayor cantidad de personas se encuentran alrededor del logaritmo del 3.75; que representan alrededor de USD 50, esto implica que hay un buen número de personas en esta provincia que reciben trans ferencias monetarias distintas a los ingresos laborales.
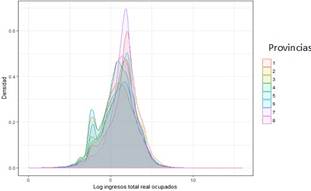
Figura 3 Función de densidad de los ingresos totales personales reales período 2006-2016 por provincia (Grupo 1).
En el segundo grupo de análisis las provincias con mayor concentración de personas alrededor de la media son: Pichincha, Guayas y los Ríos, de igual manera con el nivel más alto de ingresos respecto al resto del grupo. Seguido por las pro vincias de Manabí, Tungurahua e Imbabura en el medio, finalmente las provincias de la Amazo nía y Loja, que son las que presenta más dispersión y niveles de ingresos más bajos. La provincia que sobresale en la segunda protuberancia es la Amazonía, donde hay más concentración de personas que perciben ingresos de alrededor de USD 50 derivadas de transferencias monetarias condicionadas. El gráfico muestra las brechas en la distribución de los ingresos (vista a través de la diferencia de altura de las curvas), mientras el promedio de ingresos de Pichinchas es de USD 642 el de la Amazonía es de USD 469.
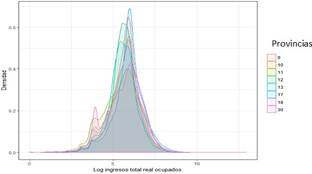
Figura 4 Función de densidad de los ingresos totales personales reales pe ríodo 2016 por provincia (Grupo 2).
Los cambios en la forma, dispersión, localización, aplastamiento de las curvas están de acuerdo a los resultados presentados por el INEC 27, se indica que al realizar un análisis por región natural en el año 2006 la región Sierra es la que más contribuye a la desigualdad (21,1 puntos o 55,8%), seguida de la región Costa (14,2 puntos o 37,5%), la Amazonía (1,4 puntos o 3,8%), el aporte de cada grupo a la desigualdad nacional se mantiene para el año 2014.
Chimborazo es la provincia que en lugar de haber mejorado la distribución de su ingreso a tenido un retroceso, ya que la distribución traslado su densidad hacia menores ingresos en 2016. La mayor parte de los ocupados tienen una condición de ocupación en otro empleo no pleno, en tercer lugar, se encuentran los trabajadores no remunerados. La media de los ingresos de la provincia en el período analizado es de USD 300 inferior al valor del salario básico unificado SBU de 2016 de USD 366.
Lo observado a través de las curvas de densidad del ingreso para las provincias del país está en sintonía con lo encontrado por varios autores que han realizado investigación a nivel territorial. Las provincias más competitivas son Guayas, Pichincha y Azuay y que concentran las tres cuartas partes de la actividad económica del país 28. En tanto que las menos competitivas son Bolívar y la Amazonia, dado que las diferencias competitivas no cambian en el corto plazo y en la ausencia de externalidades fuertes estas discrepancias se mantendrían en el corto y mediano plazo.
Pichincha presenta las condiciones más adecuadas para registrar menores niveles de desigualdad en el ingreso laboral ya que su estructura de empleo es adecuada, con los menores niveles de subempleo y desempleo y los retornos a la educación son crecientes de acuerdo a los niveles de escolaridad 29. Existe mayor concentración de capital humano en Pichincha, Napo, Galápagos, también resaltan Santa Elena y El Oro que son las ciudades que tienen mayor actividad económica, lo que les permite insertarse a mejores puestos laborales con mejores salarios 30.
Finalmente, las provincias con mayor contribución al índice de desigualdad de Theil fueron Pichincha por el lado de las ricas y Manabí por el lado de las pobres y que en general, la ubicación de las provincias en los diferentes rangos es bastante estable en el tiempo, por lo que a pesar que el índice a nivel nacional se ha reducido, las provincias siguen manteniendo su estructura de ricas y pobres a lo largo del tiempo 31.
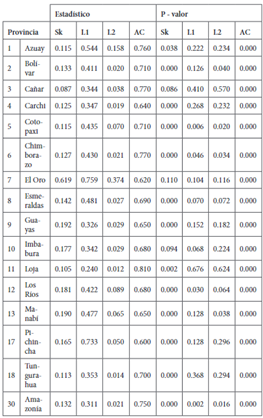
A continuación, se presentan los resultados de las pruebas aplicadas, basadas en FDE como KDE para contrastar la hipótesis nula.
De acuerdo a los resultados obtenidos, las pruebas basadas en FDE en todos los casos rechazan la hipótesis nula de la homogeneidad de las distribuciones, por su parte las pruebas basadas en la KDE, el que tuvo una tasa de rechazo de la hipótesis nula fue el estadístico AC, y el estadístico Sk, por su parte la norma L1, la L2, también rechazan la hipótesis nula las provincias cuya distribución varía en su forma, como son Chim borazo y Cotopaxi. Como se vio en el análisis gráfico muchas de las distribuciones mantienen la forma, pero presentan desplazamientos.
Análisis de la Homogeneidad de las Distribu ciones del Ingreso en el Período 2006-2016 por Actividad Económica
Se contrastó las siguientes hipótesis:
H 0 =No existen cambios en la distribución de los ingresos de la rama de actividad i entre los años 2006 a 2016
H 1 = Existen cambios en la distribución de los ingresos de la rama de actividad i entre los años 2006 a 2016
Donde i representa cada una de las ramas de actividad analizadas siendo: Agricultura, ganadería, caza, silvicultura y pesca (1), Industrias manufac tureras (2), Construcción (3), Comercio, reparación de vehículos (4), Actividades de alojamiento y servicio de comida (5), Administración pública, defensa y seguridad social (6), Enseñanza (7). Partiendo del análisis gráfico de la curva de densidad de núcleo. En cuanto a la distribución de la rama de Agricultura, ganadería, caza, silvicultura y pesca, en general no ha cambiado su forma, alcanza el pico más alto en 2008 (menor desigualdad) y en 2016 es el año con menor concentración de densidad alrededor de la media (aumento de la desigualdad), se visualizan dos modas. Apenas el 20% de la población ocupada en esta rama tiene empleo adecuado/pleno y el 36% se encuentra en otro empleo no pleno. Además, de acuerdo a la información reportada en la Enemdu de diciembre 2016 el 78.5% de la población ocupada en la Agricultura se encuentra en el área rural.
La dependencia de un sector agrícola poco productivo de parte de algunos territorios pobres y la polarización industrial en pocos cantones ricos (Quito, Guayaquil y Cuenca), estaría contri buyendo a sostener la divergencia a nivel territorial 32. Por otra parte, de acuerdo al Reporte de pobreza por consumo (2016), publicado por el INEC se concluye que la Agricultura sigue perdiendo participación en el valor agregado y en la ocupación y por ser una rama de baja productividad laboral, la disminución de empleo de este sector contribuye al aumento de la productividad laboral total 33.
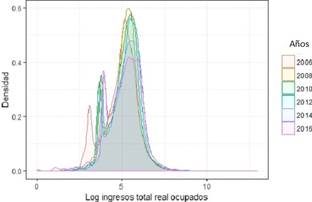
Figura 6 Función de densidad de los ingresos totales personales reales período 2006-2016 , Agricultura, ganadería, caza, silvicultura y pesca.
La industria de la Manufactura también mantiene una forma constante a lo largo de los once años con ligeros desplazamientos a la derecha, pero en general se mantiene estable. Para 2016 el 50.39% de los ocupados en la Manufactura tienen un empleo adecuado y el 62.35% se encuentra en el sector formal 34. Por otra parte, de acuerdo al Reporte de pobreza por consumo 27 del INEC, la manufactura, no ha sido de las actividades más relevantes para el país, más bien ha disminuido su importancia en el valor agregado bruto y no se ha alterado su contribución a la ocupación. Sin embargo, su contribución neta al crecimiento del PIB per cápita fue positiva debido fundamentalmente al crecimiento de la productividad dentro del sector.
La rama de la construcción es altamente concentrada alrededor de la media que no ha tenido mayores desplazamientos, ligeramente se aprecia una dispersión de la media de la distribución hacia la derecha en el año 2016. En esta rama de actividad mientras el 51% de personas ocupadas tiene una condición de empleo adecuado, el 57.7% se encuentra en el sector informal6. El INEC en su Reporte de pobreza por consumo (27 determina que la construcción fue el sector más dinámico en términos de su contribución neta al crecimiento del PIB per cápita, debido principalmente a un aumento de la productividad. Así también Larrea 34, concluye que el producto por habitante de la construcción muestra un comportamiento inestable con un perfil fuertemente procíclico. En las fases de disponi bilidad de divisas, la construcción crece tanto por la expansión de la inversión pública como por el aumento de la demanda doméstica, y disminuye fuertemente en períodos de crisis.
Al igual que las demás ramas de actividad el Comercio se ha desplazado a la derecha, para 2016 presenta un aplastamiento y se visualiza la formación de dos agrupaciones tanto hacia menores ingresos como hacia mayores ingresos, siendo esta última con mayor densidad, lo que sugiere concentración hacia los ingresos más altos. Para 2016 aportó el 10.4% del VAB, ubicándose en tercer lugar de importancia. La mayor parte de población ocupada en esta actividad se encuentra en el área urbana para 2016 representó cerca del 85%, solo el 37.9% se encuentra la ocupación plena 34. El Comercio es una de las actividades de menor productividad por debajo de la media Nacional 20.
En las actividades de alojamiento también se puede apreciar un desplazamiento a la derecha con un aplastamiento en 2016. Como porcentaje del VAB a 2016 representa el 2.3%. El 83% de los ocupados en esta rama de actividad se encuentran en el área urbana, el 87% se encuentra en el empleo inadecuado, los ocupados en esta rama se encuentra distribuidos en proporciones similares entre el sector formal (46%) e informal (48%) 29.
Desde 2001 la actividad turística es importante para el país, mediante Decreto Ejecutivo publicado en el Registro Oficial 309 de este año, se establece como Política Prioritaria de Estado el desarrollo del turismo en el país. El turismo en el Ecuador representa el tercer ingreso no petrolero para la economía.
En el proyecto del Ministerio de Turismo, Ecuador Potencia Turística se identifica como una de las deficiencias que tiene esta actividad, la falta de planificación estratégica en el área de marketing, tanto a nivel nacional como internacional 35. Los servicios de Alojamiento se encuentran dentro de los sectores de baja productividad 20. Por su parte, en el Boletín de Indicadores Turísticos del Ecuador de enero de 2017, se tiene que entre enero y diciembre de 2016 se tuvo un total de 1,412 millones de visitantes extranjeros, con un decrecimiento de 8.5% respecto a 2015. También para el cuarto trimestre de 2016 se tuvo un total de 484,884 empleados en el sector lo que representa un crecimiento de 11.7% respecto a 2015. Finalmente, el saldo de la balanza turística para el tercer trimestre de 2016 fue de 292 millones de dólares con un decrecimiento de 31.7% respecto también a 2015 36.
La rama de administración pública y defensa es la que tiene mayor concentración de la densidad en niveles de ingresos superiores al resto de ramas. Es una curva bastante simétrica lo que indica menor desigualdad al interior del grupo. Esto se puede explicar debido a que la mayoría de servidores públicos se rigen mediante la Ley Orgánica del Servicio Público, LOSEP, que norma sobre la escala de remuneraciones mensuales unificadas. En el Acuerdo Ministerial Nro. MDT-2017-0154 del 22 de septiembre de 2017 se establece un mínimo de USD 527 para el Servidor Público de Servicios 1 y un máximo de USD 4,500 para el Servidor Público 16, Grado 22. Es de las actividades que más registra ingresos altos a diciembre de 2016 el promedio de ingresos estuvo alrededor de los USD 1,123 el doble del promedio nacional.
Por otro lado, se evidencia un punto de quiebre en el número de instituciones públicas de 21.2% entre 2006 y 2007 (37). Los autores también indican que el gasto público (gasto corriente) entre 2007 y 2013 se ha incrementado en 194.9%. El componente con mayor peso en el gasto público corriente son los Sueldos, que se han incrementado en 140,9% en el período en mención. Sin embargo, los autores a partir de su análisis no pueden demostrar si el aumento se debe a un incremento de burocracia (número de empleados) o de incrementos en sueldos y salarios, o su proporción.
La actividad de la enseñanza es la que más cambios en la forma ha tenido, en 2006 esa una curva más simétrica mantiene el pico de la densidad alrededor de 0.7 hasta 2010, para 2014 y 2016 hay un desplazamiento a la derecha (incremento de los ingresos) y para 2016 es una curva con mayor concentración alrededor de la media (mayor igualdad), pero con una bimodalidad evidente. El promedio de ingresos de esta rama de actividad también está sobre el promedio nacional (USD 762 para 2016). La bimodalidad se puede explicar por cuanto es una rama de actividad heterogénea, si se analiza desde el punto de vista de la enseñanza para la educación inicial, general básica y bachillerato y para la educación superior.
A partir de la vigencia de la Constitución de 2008, aprobada mediante referendo, la Educación en el país ha tenido cambios, algunos de los cuales están relacionados o atados a temas normativos derivados de la aprobación tanto de la Ley Orgánica de Educación Superior, LOES en 20107 como de la Ley Orgánica de Educación In tercultural Bilingüe, LOEI en 20118. Dado que se está analizando los cambios en la distribución de los ingresos solo se hará mención a los aspectos relacionados con las escalas de remuneración de los docentes y sus cambios en el período analizado.
El escalafón docente para los profesores de educación inicial, básica general y bachillerato está normado en el Reglamento General a la LOEI vigente desde 2012 y sus posteriores reformas. En el Art. 301 de las Categorías del Escalafón docente se indica que está estructurado por 7 categorías con denominación alfabética desde la G hasta la A y tienen equiparación en relación a las escalas de la Ley Orgánica de Servicio Público. La categoría G es equivalente a Servidor Público 1 (USD 817) y la categoría A, a Servidor Público 7 (USD 1,676). Las remuneraciones de los docentes antes de la recategorización que se realizó luego de la expedición de la Ley y sus reglamentos eran menores, por ejemplo, un docente de hasta 14 años de experiencia podía ganar hasta USD 466,58, luego de 2012 hasta USD 817. Un docente de hasta 45 años de experiencia ganaba hasta USD 1,013.15, luego hasta USD 1,676, sin embargo, también se indica que el salario por hora disminuyó al cambiar de la jornada pedagógica a la jornada de 40 horas semanales.
Por otro lado, el escalafón y escala remunerativa del personal académico de las Universidades y Escuelas Politécnicas está normado por el Regla mento General a la LOES vigente desde octubre de 2012. En el Artículo 46.- Escalafón y escala remunerativa se expresan las categorías, niveles y grados escalafonarios. Por ejemplo, al personal académico titular principal /principal investigador a tiempo completo le corresponde en la escala de remuneraciones del sector público un Grado 19 (USD 2,670). De acuerdo a una publicación del Telégrafo antes un profesor principal ganaba USD 1,281 y después del reglamento USD 2,967, un auxiliar antes $481 y después USD 1,676 38.
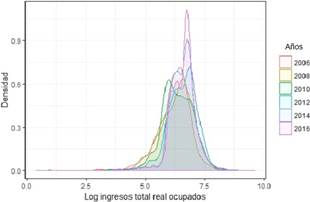
Figura 7 Función de densidad de los ingresos totales personales reales pe ríodo 2006-2016 , Enseñanza.
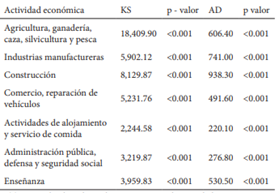
A continuación, en la Tabla 6 y Tabla 7 se presen tan los resultados de las pruebas para k muestras aplicadas.
CONCLUSIONES
Las hipótesis planteadas sobre verificar si existen diferencias en la distribución del ingreso a nivel de provincias y actividades económicas en el pe ríodo 2006-2016, con base en los resultados, se puede indicar que estas se han cumplido.
De acuerdo a la aplicación de pruebas para verificar la hipótesis de normalidad de la distribución de ingresos personales tanto por provincia como actividad económica, se obtuvo como resultado que se rechaza a hipótesis nula, en todos los casos el p valor es menor a 0.05, por tanto, la distribución de ingresos es diferente de la Normal.
La aplicación de métodos no paramétricos para el análisis de distribuciones que se alejan de los supuestos de la normal, es adecuada para el caso de la distribución de los ingresos personales ya que sus formas presentan asimetrías y en algunos casos más de una moda.
La experiencia de aplicación de pruebas de bon dad de ajuste basadas en la Función de Distribu ción Empírica que tradicionalmente se han utilizado así como la aplicación de pruebas basadas en la función de densidad KDE, como método alternativo y de desarrollo más reciente, han permitido verificar los hallazgos encontrados por Martínez y Baranzano 14, en cuanto a que las pruebas basados en KDE tienen más potencia cuando se trata de distribuciones que difieren en su forma en tanto que los basados en FDE fun cionan mejor cuando las distribuciones difieren en su localización. En el caso de Ecuador los cambios en el tiempo de la distribución del in greso corresponden a esta última característica. En este sentido se ha podido concluir que las pruebas basadas en FDE funcionan mejor para el caso de la distribución del ingreso del país. Y la prueba basada en KDE que mejor desempeño tuvo fue el estadístico AC y en menor medida la norma L1 lo que también se corrobora con la evidencia empírica.
En cuanto a la distribución de los ingresos se ha podido verificar tanto a partir del análisis gráfico como de los resultados de las pruebas implementadas que efectivamente durante el período 2006 - 2016 ha habido cambios en la distribución del ingreso, que si bien han tenido un desplazamiento sostenido hacia la derecha, en los dos últimos años se evidencia un cambio en la concentración de la densidad de niveles superiores a niveles inferiores, en los que mayoritariamente hay un aplas tamiento de la curva lo que implica aumento de la desigualdad y consecuentemente un aumento en los niveles de pobreza.
A partir de este análisis se ha podido confirmar que en el país persiste la desigualdad en el desarrollo territorial, las provincias que tradicionalmente presentan mayores niveles de pobreza y desigualdad, en los indicadores puntuales, son las mismas que tienen curvas de distribución más asimétricas y con concentraciones de población en los ingresos más bajos, siendo el caso de Chimborazo, el que más llama la atención por su marcado deterioro en la distribución del ingreso. En tanto que las provincias de Pichincha, Guayas y Azuay son las que presentan mejores niveles de ingresos y distribuciones menos concentradas. Por lo tanto, están en mejores condiciones que el resto del país en términos de la distribución del Ingreso. En cuanto a las ramas de actividad económica del análisis se desprende que, si bien se ha probado que hay cambios en la distribución en cuanto a su forma, esta se mantiene estable, igualmente se observaron cambios en la localización y la magnitud. El caso de la actividad de enseñanza es la que ha te nido el cambio más notorio, en parte se ha explicado que estos cambios están influenciados por la aplicación del escalafón docente que consta en los reglamentos de la LOEI y LOES. Por tanto, los patrones de especialización no han cambiado, al igual que los niveles de ingresos que siguen siendo bajos en el sector primario, han mejorado en el sector de la construcción que como se indi có es un sector procíclico y se mantienen en el rango más alto la enseñanza y las actividades de administración pública.
