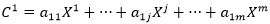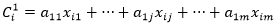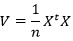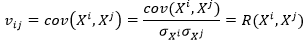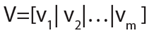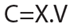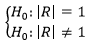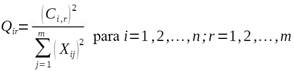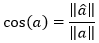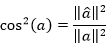I. INTRODUCCIÓN

La provincia de Chimborazo está ubicada en la región centro de Ecuador, por estar situada en la cordillera de los Andes presenta grandes elevaciones como el Chimborazo (6.310 m), tiene fértiles valles como los de Guano, Riobamba y Penipe. La provincia tiene importantes afluentes; entre los principales están: el Chambo, Chanchán y Chimbo. Debido a la presencia de masas de aire amazónicas y oceánicas; y sobre todo la altura, se presentan cuatro tipos de climas; a los 4.600 m.s.n.m. es de tipo glacial, entre los 3.000 y 4.000 m.s.n.m. es páramo, bajando; a los 2.000 m.s.n.m. el clima es mezotérmico seco; y en zonas cercanas a la costa el clima es mesotérmico húmedo y semi-húmedo. La provincia se caracteriza por ser ganadera y agrícola, por tal razón es importante analizar el comportamiento meteorológico de la velocidad de viento ¹.

El Análisis de componentes Principales (ACP) es una técnica multivariada que con frecuencia ha sido empleada en estudios meteorológicos, pues permiten identificar comportamientos en variables como: temperatura, presión, velocidad de viento; entre otras ². Se han realizado varios estudios empleando el ACP; es así que, en el trabajo: Caracterización de las sequías meteorológicas en la región central de Argentina ³, se aplicaron componentes principales para el ordenamiento de las estaciones pluviométricas; ⁴, Josué Polanco, realiza un análisis por componentes principales en la evaluación de redes de control de la calidad del aire; ⁵, Roldán emplea el ACP para determinar zonas isotérmicas y selección de estaciones meteorológicas representativas para estimar el impacto del cambio climático sobre la posible relación entre mortalidad y temperatura en la región de Argón-España; para identificar patrones de variabilidad climática; Rueda ⁶ aplica ACP, Fourier y clúster k-medias; ⁷, Ferrelli, desarrolla una regionalización climática a partir del análisis de las temperaturas y precipitaciones diarias en el sur de la Región Pampeana-Argentina; ⁸, Ramírez, en su investigación aplica un análisis multivariado de componentes principales para determinar la influencia de variables meteorológicas sobre el desarrollo fenológico de la caña de azúcar en Aguada de Pasajeros-Cuba; ⁹, Quesada, aplica un ACP con el fin de encontrar variabilidad en los datos; y así realizar una cuantificación estructural forestal según el uso de la tierra y reservas de carbono en Turrialba-Costa Rica; ¹⁰, Pineda, realiza una aplicación del índice de homogeneidad múltiples mediante el ACP a datos climatológicos de Venezuela; ¹¹, Sarricolea, con el objetivo de conocer patrones e intensidades de temperatura en la Isla de Calor Urbana en el área metropolitana de Santiago de Chile emplea mapas de intensidad y un ACP; ¹², Castillo, analizó la interacción entre los parámetros microclimáticos y variables geomorfológicas empleando un ACP para definir el comportamiento térmico de los espacios urbanos en Mendoza-Argentina; ¹³, Mejía, en su trabajo aplicó ACP para conocer el comportamiento del genotipo por ambiente de nueve variedades de algodón para los valles interandinos en Colombia, ¹⁴, Esquivel, emplea el ACP para determinar patrones húmedos y secos en la cuenca alta del río Nazas; con el fin de analizar la influencia del fenómeno climático El Niño-Oscilación del Sur; y ¹⁵, Rodríguez, realizó un análisis de deposición total en la zona protectora de los cerros de Escazú en Costa Rica utilizando un ACP para identificar las posibles fuentes de emisión.

El ACP se origina en el análisis exploratorio de datos, cuyo principal objetivo es la reducción del número de variables (dimensión), ¹⁶. Las componentes se determinan mediante combinación lineal de las variables originales mismas que deben ser linealmente independientes, ¹⁷.

Consideremos una tabla de datos X con n individuos, se busca un subespacio q-dimensional; generalmente un plano, tal que la proyección ortogonal de los n puntos sobre el subespacio tienen varianza máxima. El objetivo es conservar la información más importante reduciendo la tabla de datos en un conjunto pequeño de nuevas variables, mismo que toma el nombre de componentes principales, ¹⁸.

En primera instancia se encuentra la primera componente C¹, la cual es combinación lineal de las variables originales X^j, es decir:

()1

Donde X^j es la columna j de X, lo cual significa que el valor de C¹ para el i-ésimo individuo (mes del año) está dado por:

()2

La primera componente C¹, no engloba la información contenida en X; por lo que se construye una segunda componente principal C², luego una tercera C³; y así sucesivamente.

Las componentes principales se determinan a partir de la matriz de varianzas-covarianzas, misma que se define por:

()3

Ya que las variables están centradas y reducidas entonces V=R, por lo que la matriz de correlación será:

()4

Es decir, RЄM_mxm donde R=(1/n) X^t X. Los vectores y valores propios se calculan cuando se ha definido la matriz R, ¹⁹. Si denotamos por λ₁, λ₂,…,λ_m estos valores propios ordenados de mayor a menor; y por v₁,v₂,…,v_m los respectivos vectores propios, entonces se construye la matriz VЄMmxm como:

()5

Donde, la matriz V tiene como columnas los vectores v₁,v₂,…,v_m. El cálculo de la matriz de componentes principales CЄM_mxm se realiza como:

()6

El ACP es una primera técnica que se emplea para determinar variables ocultas que puede generar inconsistencia en el conjunto de datos ²⁰.

II. MATERIALES Y METODOS

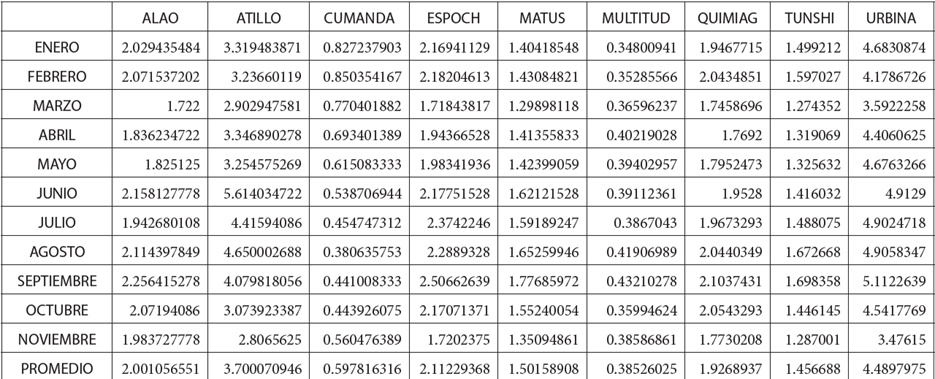
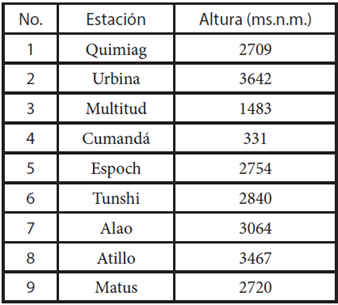
En la provincia de Chimborazo se han instalado estaciones meteorológicas con varios sensores que miden variables como: velocidad de viento (vv), radiación solar global, temperatura, precipitación, entre otras. Los datos empleados en el trabajo corresponden a los promedios por mes del año 2015 de la variable velocidad de viento (km/h), información obtenida de las estaciones meteorológicas: Alao, Atillo, Cumandá, Espoch, Matus, Multitud, Quimiag, Tunshi y Urbina; ubicadas en la provincia de Chimborazo. El equipo utilizado para la medición de la vv es un ultrasonic anemometer 85000, mismo que se encuentra ubicado a 9m del suelo; la información se registra en un dataloger y de forma automática migran a un servidor. Los datos se muestran en la Tabla 1:

Tabla 1 Base de datos, variable vv 

El análisis de componentes principales se realizó mediante la librería Factoshiny de R, y para ello se procedió a cargar el fichero y a seleccionar ACP.

Para comprobar que las correlaciones entre las variables son distintas de cero de modo significativo, se aplicó el test de Barlett; el cual verifica si el determinante de la matriz R es distinto de uno; para lo cual se contrasta:

()7

A valores altos, el test rechaza la hipótesis nula, lo que determina que el ACP no es adecuado; pues la matriz de correlaciones no es la matriz identidad, ²¹.

Para determinar si las correlaciones entre las variables son suficientemente pequeñas, se empleó la medida de la adecuación muestral de Kaiser-Meyer-Olkin (KMO), ²². Este estadístico varía entre 0 y 1, y considera que si 1 ≤ KMO ≤ 0.9 el modelo es muy bueno y conforme éste decrece el modelo es considerado como inaceptable.

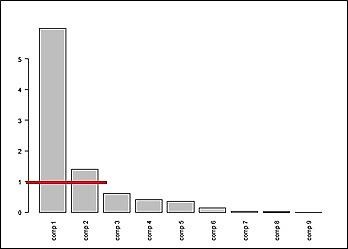
El número de componentes se determinó mediante el gráfico de sedimentación, mismo que muestra la cantidad de varianza explicada. El criterio empleado fue calcular el promedio de los autovalores y considerar la matriz de correlaciones; el cual debe ser 1 (KMO); ²³.

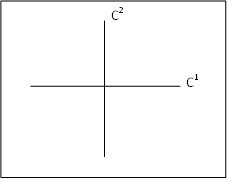
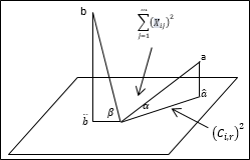
Dos gráficos utilizados en el ACP, son el plano principal y el círculo de correlación. El primero permitió identificar las similitudes entre los individuos (meses del año), conocidos como clústeres. El gráfico depende del número de componentes con los que se desea trabajar; la Figura 1, muestra un caso particular para dos componentes C¹ y C².

Figura 1 Plano principal 

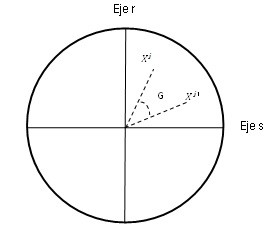
El círculo de correlaciones, Figura 2; muestra la correlación entre las variables (estaciones meteorológicas), para lo cual se analiza el ángulo que se forma entre éstas.

Figura 2 Círculo de Correlación 

Si X^j y X^j' están cercanas entre sí, entonces se presenta una correlación fuerte y positiva, si el ángulo es cercano a 90º no existe correlación entre las variables; y existe una correlación fuerte y negativa si X^j y X^j' están opuestas al vértice (origen).

La interpretación de las componentes se efectúa mediante la sobre posición de plano principal y el círculo de correlación, lo cual permite interpretar a que grupo pertenecen los individuos, ²⁴.

Una manera de determinar las calidades de los individuos y las variables; es calculando los cosenos cuadrados, ²⁵. Si QЄM_nxm, los cosenos están dados por la ecuación:

()8

Sean a y b dos individuos, con â y b̂ las proyecciones sobre un plano principal, Figura 3; se puede observar que representa mejor a a que lo que b̂ lo hace con respecto a b; pues se observa un vector más grande, por lo que podemos decir que a y b están mejor representados si α y β son pequeños. Sabemos que si un ángulo tiende a cero entonces su coseno tiende a 1, por lo que podemos calcular:

()9

Para evitar valores negativos se considera:

()10

Por lo que; si el cos²(a)es cercano a 1 la representación del individuo será muy buena y mientras más pequeño sea este valor la representación es mala (cercano a 0).

Figura 3 Proyección de individuos en plano principal 

III. RESULTADOS Y DISCUSIÓN

La prueba de Barlett Figura 4, muestra que con un nivel de significación del 0.05 rechazamos la hipótesis nula de esfericidad, esto ya que el p-valor < 0.05 por lo que el análisis de componentes principales se puede aplicar.

Figura 4 Test de Barlett, variable vv 

Figura 5 Gráfico de sedimentación, variable vv 

El gráfico de sedimentación, Figura 5 permitió identificar dos componentes principales, pues con éstas se alcanza un 82.291% de información en las variables; tal como muestra la Tabla 2.

Tabla 2 Varianza Explicada, variable vv 

Los gráficos obtenidos para esta variable se muestran en la figura:

Figura 6 Variable velocidad de viento: (a) Plano principal (b) Circulo de correlaciones 

El plano principal, Figura 6 (a); muestra que la velocidad de viento es similar en cuatro grupos, mismos que están conformados por: grupo 1 (azul); enero y febrero, grupo 2 (verde); marzo, abril, mayo y noviembre, el grupo 3 (naranja) por junio, julio, agosto y septiembre y en el cuarto octubre (rojo).

El círculo de correlación, Figura 6 (b), muestra que exite una correlación alta y positiva entre Quimiag y Tunshi; así como entre Alao y Espoch. No existe correlación entre Quimiag y Multitud; además, existe un correlación fuerte y negativa entre Cumandá y Multitud. Se puede observar que el eje uno (horizontal) contrapone las estaciones que se encuentran a una altura superior a los 1000 m.s.n.m. con aquella que presenta un valor inferior a este, Tabla 4.

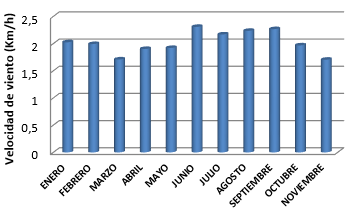
De acuerdo a la sobre posición del círculo y el plano principal podemos decir que la velocidad de viento en los meses de junio, julio, agosto y septiembre es predominante en las regiones donde se encuentran ubicadas las estaciones de Urbina, Matus, Atillo y Multitud; pero existe una relación negativa en los meses de marzo, abril, mayo y noviembre; sobre todo en marzo, pues es el más alejado; esto se debe a que durante esos meses la vv no superó los 2km/h, Figura 7.

La vv en la estación Cumandá es representativa en los meses de enero y febrero; cabe indicar que esta estación es la única que se encuentra ubicada a una altura inferiror a los 500 m.s.n.m., Tabla 4. En octubre la vv fue predominante en las estaciones de Quimiag, Tunshi, Alao y Espoch; las cuales se encuentran ubiadas a una altura comprendida entre los 2000 y 3100 m.s.n.m., Tabla 3.

Figura 7 Valores medios mensuales de velocidad de viento 

Tabla 3 Altura estaciones meteorológicas 

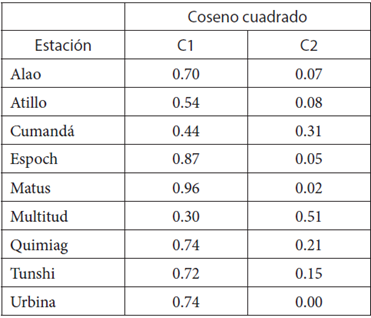
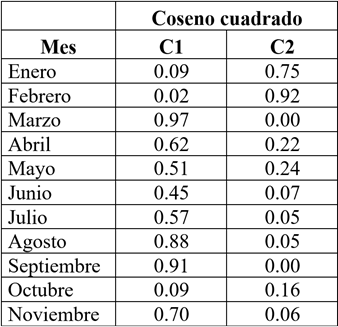
Los cosenos cuadrados mostraron que la variable con baja representación en la componente 1 (C1) es Multitud y la que mejor representa es Matus con valores de 0,30 y 0,96 respectivamente, Tabla 4. Para la componente 2 (C2), Multitud es la variable mejor representada con un coseno cuadrado igual a 0,51; mientras que Urbina y Atillo tienen una representación baja, Tabla 5.

Tabla 4 Cosenos cuadrados de variables, vv 

Tabla 5 Cosenos cuadrados de los individuos, vv 

IV. CONCLUSIONES

El análisis de componentes principales pudo identificar características comunes de velocidad de viento en la provincia de Chimborazo. Este estudio mostró dos tipos de comportamientos; el primero lo determina la región norte de la provincia, con zonas ubicadas a una altura superior que los 1.000 m.s.n.m.; y el segundo corresponde a la región del subtrópico; misma que posee mayor diversidad con fauna y flora totalmente diferente a la anterior. Cabe destacar que la región donde se encuentra ubicada la provincia, recibe influencia alternada de masas de aire oceánicas y amazónicas, haciendo que el aire húmedo y cálido se eleve y enfríe produciendo altas precipitaciones y ecosistemas húmedos. Los resultados del estudio pueden ser de utilidad para identificar zonas con velocidades de viento que pueden incidir en el ecosistema de la provincia de Chimborazo, además es un preámbulo a estudios relacionados con energía eólica.