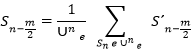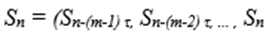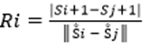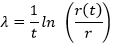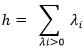I. INTRODUCCIÓN

El material particulado de 2.5 micras (PM2.5), conocido como polvo en suspensión es respirable debido a su dimensión aerodinámica y al ingresar al sistema respiratorio puede alojarse permanentemente en los alvéolos pulmonares con efectos adversos para la salud ¹. Este contaminante atmosférico se origina a partir de la combustión de combustibles fósiles, procesos industriales, agricultura, construcción de carreteras, procesos erosivos y la extracción de material pétreo ². En la atmósfera urbana el 70% y 80% de PM2.5, se origina por el tráfico vehicular ³. El valor fijado por la Organización de la Salud para concentraciones anuales de PM2.5 es de 10 μg/m3. El resultado del estudio de calidad del aire realizado entre el 2016 en el Distrito Metropolitano de Quito supera las normas nacionales y de la OMS ⁴.

El control de la contaminación por PM2.5 pasa por diferentes etapas, desde las normativas, políticas, educativas y técnico científicas, cuya efectividad de pende de su cumplimiento y avance tecnológico-científico, lamentablemente desde el punto de vista científico presenta grandes dificultades por ser un sistema complejo, impredecible y aparentemente caótico ⁵. Los especialistas en dinámica no lineal usan la palabra “caos” como un término técnico con un significado matemático preciso para definir un comportamiento irregular e impredecible de un sistema que es determinístico y no lineal ^6,7.

Desde el descubrimiento de la impredecibilidad en los sistemas determinísticos, los cuales conllevaron al estudio de sistemas dinámicos, muchos trabajos de investigación fueron desarrollados para encontrar las propiedades del caos con los cuales poder clasificar estos sistemas ^8,9. Por ejemplo, indicadores dinámicos como la sensibilidad a las condiciones iniciales, los exponentes de Lyapunov, la entropía de Kolmogorv-Sinai, entre otros, fueron desarrollados para hacer una caracterización más precisa de estos sistemas ^10,11.

Así, por ejemplo, aparecen los denominados “sistemas-K” que exhiben una propiedad matemática conocida como “mezcla”, es decir una entropía de Kolmogorv-Sinai positiva. Esto significa que los sistemas en cuestión son extremadamente sensibles a las condiciones iniciales, de modo que dos trayectorias inicialmente próximas divergen según una tasa exponencial. Esta tasa es medida por los exponentes de Lyapunov, que son equivalentes a la entropía de Kolmogorv-Sinai y pueden ser fácilmente calculados, para establecer el grado de coticidad y la factibilidad de que puedan ser predichos ¹².

Con estos antecedentes el objetivo de la investigación es analizar el grado de predictibilidad de las concentraciones de PM2.5 del período 2005-2016 monitoreados en Quito-Ecuador, mediante sistemas dinámicos no lineales en base a la entropía de Kolmogórov-Sinai ¹³.

II. MATERIALES Y MÉTODOS

Para el análisis de las concentraciones de material particulado PM2.5 del período 2005-2016 en Quito-Ecuador, se utilizaron los datos históricos de las registrados Red de Monitoreo Atmosférico Metropolitano de Quito. Para el análisis no lineal se aplicó los programas del modelo Tisean v.2.0 ¹³.

Para la reducción del ruido se utilizó el programa nrlazy, para calcular el Tiempo de Retardo se utilizó el programa mutual, para la dimensión de encaje el programa false neighbors y para los Exponentes de Lyapunov el programa lyap_spec. Para el análisis de la entropía Kolmogórov-Sinai se sumaron los exponentes positivos de Lyapunov de cada año.

Reducción del ruido

El estudio de series de datos puede llevar a sacar conclusiones erróneas ya que los datos que se toman como magnitud de la variable a analizar suelen estar influidas por varios factores que introducen distorsiones a las que se denomina ruido y por lo tanto no permiten observar con claridad los patrones dinámicos que se quiere analizar ¹⁴. El algoritmo no lineal más simple para la reducción de ruido consiste en reemplazar la coordenada central de cada vector de encaje, por un promedio local de esta coordenada, como se expresa en la Ecuación 1:

()1

Al escoger una m dimensión de encaje y un adecuado tiempo de retardo τ, por cada vector de encaje Sn se forma una vecindad Une, se forma en el espacio de fase que contiene todos los puntos Sn tal que ||Sn-S´|| < ε, donde ε es el radio de la vecindad, que debe ser lo suficientemente grande para cubrir la extensión de ruido y S´ el espacio de fase inicial ¹⁵. Por cada vector de encaje Sn = (Sn-(m-1),....Sn) con λ=1, la coordenada corregida es Sn-(m/2), se calcula como el promedio sobre la vecindad Une.

Tiempo de Retardo

El tiempo de retardo, es el paso más importante en el análisis del espacio de fases, es la técnica de reconstrucción del sistema, formando vectores y ejecutando una proyección en el espacio de fases, que es un espacio físico que permite detectar variables dinámicas, en este método se busca la relación biunívoca de los datos en el espacio de las fases ¹⁶.

El método de reconstrucción de espacio de fase más importante es el método de retardo. Los vectores en un nuevo espacio, el espacio de empotramiento, se forman a partir de los valores retardados de las mediciones escalares expresado en la Ecuación 2:

()2

El número m de elementos se denomina dimensión de retardo, el tiempo τ se denomina generalmente retardo. Los teoremas incorporados por Takens ¹⁷ y por Sauer, Yorke and Casdagli, concluyen que Sn son mediciones escalares del estado de un sistema dinámico, entonces bajo este criterio, la incorporación de retardo de tiempo proporciona una imagen uno a uno del conjunto original x siempre que m sea lo suficientemente grande. Si N mediciones escalares están disponibles, el número de vectores de inclusión se estima que será N-(m-1)τ ¹⁸.

Dimensión de Encaje

La idea del algoritmo del falso vecino es que para cada punto Ṧi en la serie de tiempo busque su vecino más cercano Ṧj en un espacio m-dimensional. Por lo tanto, calcula la distancia ||Ṧi - Ṧj||, que reincide en ambos puntos. Como se expresa en la Ecuación 3:

()3

Al exceder Si un umbral heurístico determinado St, este punto está marcado como un vecino falso vecino ¹⁸. El criterio de que la dimensión de encaje es lo suficientemente alta, es la fracción de puntos para la cual Si > St es cero, o al menos suficientemente pequeño. Si la relación de la distancia de la interacción y del vecino más cercano excede a un valor determinado, el punto se marca como un vecino equivocado ¹⁹.

Exponentes de Lyapunov

El cálculo del espectro completo de Lyapunov requiere considerablemente más esfuerzo que el exponente máximo ²⁰. El proceso consiste en una estimación de los Jacobianos locales, es decir, de la dinámica linealizada que gobierna el crecimiento de las perturbaciones infinitesimales. El caos surge del crecimiento exponencial de las perturbaciones infinitesimales es así que para garantizar el análisis de esta inestabilidad están los exponentes de Lyapunov, que cuantifican el momento que dos trayectorias se alejan, como se expresa en la Ecuación 4:

()4

Donde: r(t) es el semi-eje mayor de una elipse, r es el radio pequeño y t es el tiempo grande, en general se establece λ1 ≥ λ2………λd. En un sistema caótico al menos un exponente de Lypunov es positivo ²¹.

Entropía de Kolmogórov-Sinai

Este tipo de entropía también llamada métrica (h), mide la pérdida de información a lo largo de la evolución del sistema. Como se expresa en la Ecuación 5, este tipo de entropía es determinada por la suma de exponentes positivos de Lyapunov ^22,23. Tiene importante significado cuando se aplica a sistemas de los cuales no se dispone más que de series temporales de valores de determinada variable.

()5

Este tipo de entropía se relaciona con la previsibilidad que expresa una escala de tiempo promedio hasta la cual las predicciones pueden ser posibles ²⁴. Esta cantidad invariante intrínseca del sistema tiene una relevancia singular para la caracterización de la previsibilidad ²⁵. Los valores más altos de h implican valores más bajos de la predictibilidad 1/h, es decir, cuanto más caótico, menos predecible.

III. RESULTADOS

A continuación, se exponen los resultados del procesamiento las series de datos anuales de las concentraciones de PM2.5 dentro del período 2005-2016.

Tabla 1 Tiempo de Retardo y Dimensión de Encaje 

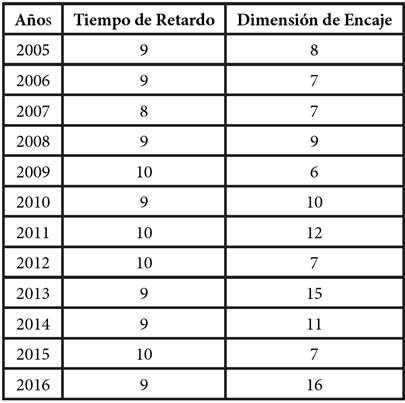
En la Tabla 1, se indican los valores del Tiempo de Retardo que representan los primeros mínimos de la función de correlación mutual informatión, en el espacio de las fases, además de los valores de la Dimensión de Encaje que usa la función false neighbors, en la cual debe ser cero su valor para tener el valor óptimo de dicha dimensión ¹¹, estos resultados permiten reconstruir la serie de datos en el espacio de las fases y determinar los coeficientes de Lyapunov.

Tabla 2 Exponentes positivos de Lyapuvov 

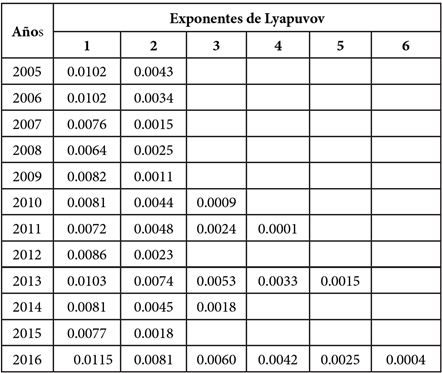
En la Tabla 2, se observan los resultados de los cálculos de los exponentes de Lyapunov positivos encontrados en la serie de datos, que permiten establecer que es un sistema hipercaótico.

Tabla 3 Entropía de Kolmogórov-Sinai 

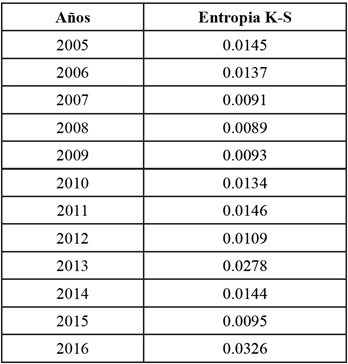
En la Tabla 3, se encuentran la sumatoria de los exponentes de Lyapunov positivos que conforman los valores de la Entropía Kolmogórov-Sinai (K-S).

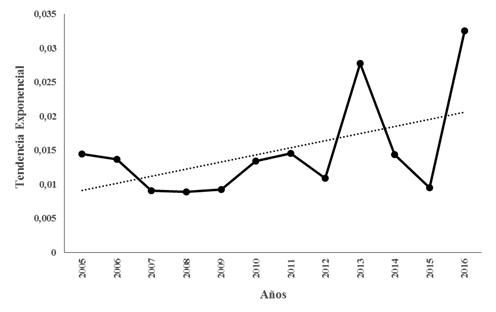
Figura 1 Entropía de Kolmogórov-Sinai para las concentraciones anuales de PM2.5 del período 2005 - 2016 

En la Figura 1 de la Tabla 3, se puede observar una tendencia aumentar de la entropía de Kolmogórov-Sinai.

IV. DISCUSIÓN

En el procesamiento de las series de datos anuales de las concentraciones de PM2.5 dentro del período 2005-2016, se identifican variaciones significativas a partir del año 2010 tanto en los valores que constituyen la reconstrucción de los datos en un espacio multidimensional que determinan el Tiempo de Retención como en la dimensión mínima en el espacio de las fases referentes a la Dimensión de Encaje.

El número de exponentes positivos de Lyapunov, demuestran que existen perturbaciones infinitesimales en las series de datos de las concentraciones anuales de PM2.5, cuya sumatoria establece una tendencia creciente a partir del año 2010 que se incrementa drásticamente en los años 2011, 2013 y 2016, dentro el principio de la entropía de Kolmogórov-Sinai estos valores se interpretan como la pérdida de información en la serie de datos, que a medida que se incrementan dificultan más la predictibilidad del sistema usando la teoría del caos.

V. CONCLUSIONES

El número de exponentes de Lyapunov, establecen en promedio una dinámica hipercaótica, al presentar más de un coeficiente positivo en los 12 años analizados.

La tendencia de los valores que representan la entropía de Kolmogórov-Sinai es creciente, por lo que se determinan que la predictibilidad para las concentraciones anuales de PM2.5 es cada vez menos probable usando la teoría del caos, debido a la pérdida de información del sistema en el tiempo.