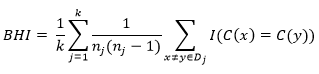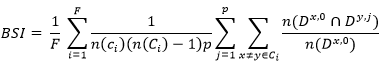I. INTRODUCTION

Cluster analysis is an important exploratory tool widely used in many areas such as biology, sociology, medicine and business, and the objective of cluster analysis is to assign objects in a group and establish in meaningful classes so that objects in the same class are more similar among themselves than to those of other classes ¹.

The world of science has changed, and there is no doubt about this. The new model consist of data is captured using instruments or generated through simulations before processing with software. The resulting information or knowledge are collected on computers. Scientists look at the data rather late in this sequence. Scientists only get to look at their data quite late in this sequence. The techniques and technologies for such data intensive science in data are so different that it is important distinguishing data intensive science from computational science as a new paradigm: the fourth paradigm for scientific exploration ².

In a clinical application of microarray- based cancer diagnosis, an important statistical problem associated with the classification of tumors, the identification of new classes of tumors using gene expression profiles ³, hence the importance of the analysis.

Database: The database consists of: using a combination of genetic marker / selective isolation of progenitor cells embryonic pluripotent and technology of micro arrays based on oligonucleotides to delineate and compare the "molecular fingerprint" of two populations into various lineages of mesenchymal cells in the developing embryonic orofacial region. The first branchial arches (bilateral tissue primordia that flank the primitive oral cavity) are populated by pluripotent mesenchymal cells of two different lineages: neural crest (neuroectoderm) and mesenchymal cells derived from the mesoderm. These cells give rise to all the elements of the connective tissue (bone, cartilage, smooth and skeletal muscle, dentin) of the orofacial region (maxillary and mandibular portion), as well as the neurons and glia associated with the cranial ganglia, among other tissues ⁴.

Microarray or Biochips: The genome of human beings is a set of genes which are distributed in chromosomes. Likewise, genes are DNA sequences that contain all information needed to synthesize proteins, molecules essential for life that perform virtually cell functions. When a gene is "activated" to give rise to corresponding protein, therefore this gene is being expressed in the cell ⁵.

Figure 1 The laser excites the fluorescence of the cDNA, generating signals for the encoding of a microarray ⁶  

A collection of gene expression data can be seen abstractly as a table with rows representing genes, columns that represent several samples and each position in the table that describe the measurement of a specific gene in a particular sample. This table is called a gene expression matrix. In addition to the matrix, a description of a microarray experiment should also contain information about the genes whose expression has been measured and the experimental conditions in which the samples were taken. The information required to describe a microarray experiment can be conceptually divided into three logical parts: genetic annotation, sample annotation and a gene expression matrix ⁷.

New techniques in biotechnology, such as microarrays of cDNA and oligonucleotide chips of high density, allow simultaneous monitoring of the expression of thousands of genes in any desired number of conditions ⁸.

Clustering methods

K-Means: The algorithm K-Means is a typical method of clustering based on division. Given a certain K value, the algorithm divides the data into K disjoint groups. The K-means algorithm is simple and fast. The complexity is O ( l * k * n ), where l is the number of iterations and k the number of clusters. Furthermore, this algorithm converges normally in a reduced number of iterations ⁹.

K-means is a very popular method for general grouping. In K-means the clusters are represented by mass centers of the members, and it can be shown that the K-means algorithm by switching between assigning membership to the cluster for each data vector to the nearest cluster center and calculate the center of each cluster as the centroid of its member data vectors is equivalent to finding the minimum of a sum of squares cost function using the coordinate offspring function ¹⁰.

The K-means algorithm is sensitive to outliers since an object with an extremely large value can substantially distort the data distribution. How could the algorithm be modified to decrease that sensitivity? Instead of taking the average value of the objects in a cluster as a reference point, a Medoid can be used, which is the most centrally located object in a cluster. Therefore, the partition method can be performed based on the principle of minimizing the sum of the differences between each object and the reference point corresponding. This forms the basis of the K- Medoids method ¹¹.

Hierarchical clustering with correlation (Hierarchical): This algorithm produces a hierarchy of clusters rather than a fixed set number of clusters in advance. At the basic or initial level, each observation forms its own group. At each subsequent level, the two "closest" groups combine to form a larger group. The "average" method is used, which means that “distance" between the groups is the average ¹².

Diana: At each step, a divisive method divides a group into two smaller ones, until; finally, all groups contain a single element. This means that the hierarchy is built again in n-1 steps when the data set contains n objects. A divisive analysis proceeds by a series of successive divisions. In step 0 (before starting the algorithm), all the objects are together in a single cluster. In each step, a group is divided, until in step n-1 all objects are separated (forming n groups, each with a single object) ¹³.

Agglomerative nesting: Agnes function: The Agnes function is of the hierarchical agglomerative type; therefore, it produces a sequence of clusters. In the first grouping, each of the n objects forms its own separate group. In later steps, the groups are merged, until (after n - 1 steps) there is only one large group 18. There are many of these methods. In Agnes, the group average method is taken as the default, based on robustness, monotonicity and consistency arguments ¹⁴.

Clustering Large Applications (Clara): It can deal with much larger data sets. Internally, this is achieved by considering subsets of fixed size (size) data so that time and storage requirements become linear is at n instead of quadratic ¹⁵.

Partition around the medoids (Pam): The pam algorithm is based on the search for k representative or medoid objects among the observations in the data set. These observations should represent the structure of the data. After finding a set of k medoids, k clusters are constructed by assigning each observation to the nearest medoid ¹⁵.

Biological Validation Measures: Biological validation evaluates the ability of a clustering algorithm to produce biologically significant clusters. A typical application of biological validation is in microarray data, where the observations correspond to genes (where "genes" could be open reading frames (ORF), expressed sequence tags (EST), analysis tags of expression of genes (SAGE), etc.). There are two measures available, the biological homogeneity index (BHI) and the biological stability index (BSI) ¹⁶.

These measurements can also be used for any other molecular expression data. The biological homogeneity index (BHI) and the biological stability index (BSI) both assess the performance of an algorithm to produce biologically similar groups. Internal validation measures provide guidelines on the statistical properties of clusters ¹⁷.

Biological Homogeneity Index (IHB): This simple measure is easy to interpret and put into practice once the reference collection of functional classes is in place. This also works with the superposition of functional classes. This measure can be thought of as an average proportion of gene pairs with matching functional classes that are statistically grouped together based on expression profiles.

Formula for calculating the index of biological homogeneity.

()1

Where k is the number of statistical clusters and for the cluster D_j, n_j = n(D_jÇC) is the number of annotated genes in D_j, and where for a set A, n(A) denotes size or cardinality ¹⁸.

Biological Stability Index (BSI): Next, the stability of a clustering algorithm is captured by inspecting the consistency of the biological results produced. When an observation unit reduces the expression profile:

Formula for calculating the biological stability index.

()2

The calculation of this index consists of 4 steps, but it is very flashy to perform manually, and this one is usually done in software, if someone want to know how to perform the calculation, review ¹⁸ “Biological stability index”.

II. MATERIALS AND METHODS

It is a quantitative, descriptive exploratory and non-experimental cross-sectional investigation.

The “R and R-Studio” software was used, as well as the “Package clValid” version 0.6-6 wich was published on March, 2008.

The package RV clValid contains functions, which allow the results validation of a cluster analysis. There are three main types of cluster validation measures available, "internal", "stability" and "biological" ¹⁶.

It was used data from an Affymetrix micro matrix experiment that compares the gene expression of mesenchymal cells of two different lineages, neural crest and mesoderm derivative. The data set consists of 147 genes and EST, which was determined a significant different expression between the two cell lines, with at least a 1.5-fold increase or decrease in the expression. There are three samples for each of the cells derived from the neural crest and the mesoderm, so the expression matrix dimension is147 6. For a more detailed description of the data set and experiments ¹⁶ originally presented in ⁴.

The objective of the study is that the biological stability index and the homogeneity index approach to the unit, indicating that they are the optimal clusters for this data set.

Grouping methods such as: Hierarchical, K-means, Agnes, Diana, Pam, and Clara were applied. Besides, for each one, it was calculated an index with different numbers of clusters, all the code used could be found on the Rpubs website: (http://rpubs.com/SenseiDewey7991/520472).

III. RESULTS

Biological Stability Index Results: As it has been mentioned in ¹⁹ that a cluster result can be considered as a partition of objects into groups. Using the “R Software” and the “ClValid Package” the calculation of the biological stability index for each grouping method was performed regarding the determined number of clusters or groupings. A cellular process of interest may involve a relatively small subset of the genes in the data set ²⁰, thus, it must be determined the best grouping method or clustering algorithm, to do so, a line - point graph was made in order to analyze the trend of the Biological stability index, it is observed that the tendency seems to have an exponential decay of the BSI in all the methods, that is to say that this index decreases as the number of clusters increases, it indicates that the stability index advise working with fewer clusters. For more consistent answers from this database, see (Figure 2).

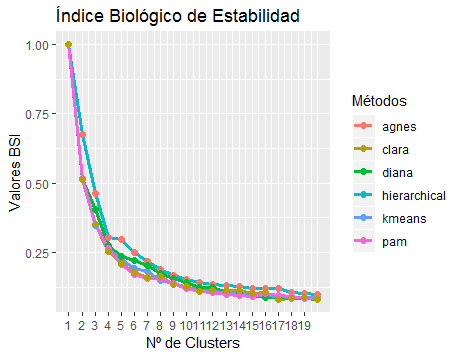
Figure 2 Graph of lines and points developed for the analysis of the trend of the BSI according to the number of groups and methods. 

Biological Homogeneity Index Results: It has been observed that as the number of clusters increases the values of the IHB also increase the opposite of the BSI, for 6 groups the Diana method stands out with a score of 0.2194 which remains a small value, for 8 groups it is obtained the highest score which is 0.2889 by the Hierarchical and Agnes methods, which represents a higher average proportion of gene pairs with matching functional classes that are statistically grouped together based on their expression profiles. BHI values are graphically represented in (Figure 3).

Figure 3 Graph of lines and points developed for the analysis of the trend of the IHB according to the number of groups and methods. 

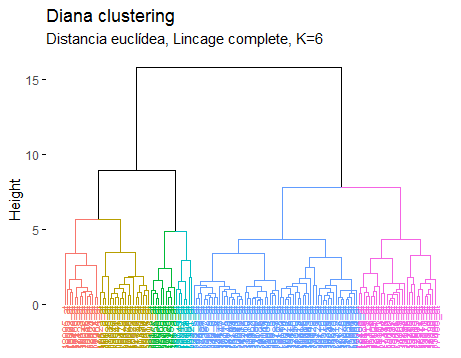
Choice of the appropriate number of clusters: One of the evaluation criteria for gene clustering methods is based on their ability to reconstruct the true underlying clustering structure ²¹, then once analyzed the trend of the indices based on the number of clusters, for this data base of The lowest number of clusters will be chosen as stated in the results presented by the stability index, but taking into account the IHB suggestion that it was 8 clusters with the Hierarchical method, and the Diana method will also be represented with 6 clusters, this is presented in Figure 4 and Figure 5:

Figure 4 Dendogram for k = 8 

Figure 5 Dendogram for k = 6 

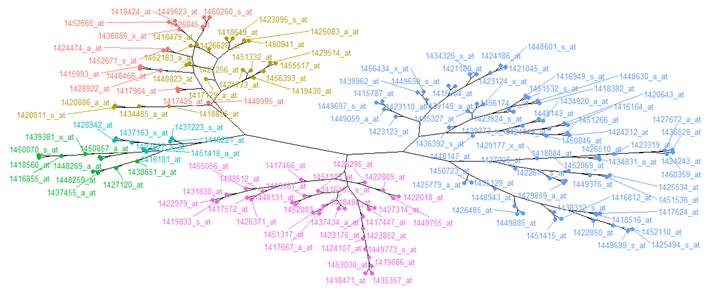
It has been observed in illustration 3 and 4, how the groupings are distributed do not vary significantly from one another, so the Diana method is chosen regarding a BSI of 0.221188 and a BHI of 0.219427 with 6 clusters due to it is the most reliable answer, indeed, it is also verified in the phylogenetic graph (Figure 6) that there could be a relation of genes according to the ramifications they present, therefore it is a possible grouping solution.

The capability to quantify the expression of thousands of genes at the same time has changed the biomedical research surface, besides it allows the analysis of the gene expression pattern at the whole genome scale ²² which makes that the result obtained be helpful for explaining the correct genes clustering.

Figure 6 Phylogenetic Graph for the Diana method with 6 clusters 

IV. DISCUSSION

In this study conducted with mesenchymal cells of two different lineages, neural crest and derived from the mesoderm, the conclusion could be established due to the phylogenetic graph (graph for the analysis of the genes) aid, and the biological indices, that the optimal number of clusters is six with the Diana Method, in article ¹⁸ it is concluded that the final result depends largely on the grouping method used.

Besides, this study allows proving once again that for different number of clusters and different methods the biological indices vary. In ²³ the results obtained show that all the methods mainly have clusters with an almost equal good performance, which in this investigation shows that there is a very similar performance in the clustering methods.

In other publications as in ²⁴ it is mentioned that genes of similar function are grouped together, furthermore, regarding the genes clusters developed in this investigation it could be stated that each gene cluster behaves similarly. It is very important to emphasize that the unsupervised methods based on existing clustering generally suffer from significantly high false alarms ²⁵ thus the results may not be completely accurate.

In the article published for the clValid package ¹⁶ there is an overview about usage analysis is also made, with the mouse database, but it was not possible to make a comparison with this study since in that investigation another method of annotating genetic expressions was used and also other grouping methods which were not considered in this study. There are limitations in this work since there are many publications with different techniques as in ²⁶ where other and more clustering techniques are used.

V. CONCLUSIONS

It could be evidenced that it is suitable to make a comparison between the different existing methods to group genes: the graphic method allows the researchers to have an idea about the grouping process the data tends to present; while the analytical method aids to determine the appropriate number of clusters; in addition to the method of grouping, which is seems as a great assistance for the analyst, the results found were compared with the phylogenetic graph which offers another perspective of the way in which the genes are grouped, therefore, a study should be carried out since these methods are supposed to be specific for the validation of genetic clusters and should coincide indeed.