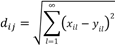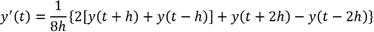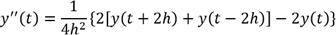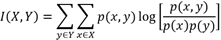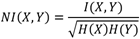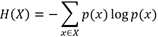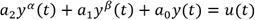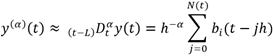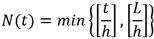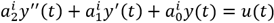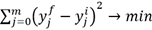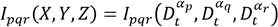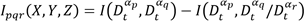I. INTRODUCCIÓN
El análisis de datos ha sido empleado como herramienta en la investigación científica para entender la dinámica de fenómenos complejos mediante el uso de herramientas matemáticas y estadísticas. El escalado multidimensional (MDS) permite visualizar el comportamiento de los sistemas y capturar la evolución espacio temporal1,2. El método permite identificar diferentes particularidades de datos, agrupando con parámetros apropiados3. Junto con la transformada de Fourier, MDS ha sido empleado para identificar patrones en variables económicas 4.
El cálculo fraccional (CF) amplía la perspectiva de las investigaciones, en donde se ha aplicado Fractional State Space Portrait (FSSP) para identificar clústeres en grupos de datos macroeconómicos y bursátiles 5. Sin embargo, la aplicación de estos métodos no se limita exclusivamente al campo económico, es aplicable en ciencias ambientales donde se requiera encontrar patrones que marquen trayectorias de comportamiento en sistemas dinámicos, tal es el caso de las variables meteorológicas como la temperatura, donde Machado sugiere adoptar la información mutua multivariante para proponer un orden de derivada óptima que ha dado como resultado una visualización mejorada del sistema dinámico de temperaturas en planeta Tierra. De manera análoga se ha podido aplicar el método para revelar patrones en otros sistemas dinámicos 6,7,8.
Ecuador es un país con gran potencial solar9, el cual se encuentra atravesado de norte a sur por la cordillera de Los Andes que divide al país en regiones naturales. En la región montañosa de la sierra central se encuentra la provincia de Chimborazo, en donde se ha instalado una red de estaciones meteorológicas automáticas, las cuales han medido y transmitido datos atmosféricos desde su instalación en 2013. Desde entonces se han desarrollado estudios10,11 en los cuales se han determinado las relaciones lineales empleando el coeficiente de Pearson y a la vez se han creado modelos para la estimación de otras variables meteorológicas 12. Sin embargo, el análisis de linealidad se vuelve insuficiente para comprender un sistema tan complejo como el meteorológico, para el cual se requiere estableces las relaciones ocultas entre sus diferentes variables.
Para tal propósito, los autores emplean el concepto de cálculo fraccional mediante el FSSP en una serie de temperaturas de 365 días del año 2015, procedente de 11 estaciones meteorológicas distribuidas en la provincia de estudio. Estos datos se interpretan como un sistema dinámico con evolución espaciotemporal correspondiente a cada estación durante el año de estudio, tales variables a su vez forman subsistemas relacionados entre ellos6. Una vez obtenido el orden óptimo de la derivada, se realizó la comparación entre FSSP y MDS para contrastar la representación visual del comportamiento dinámico del sistema.
II. MATERIALES Y MÉTODOS
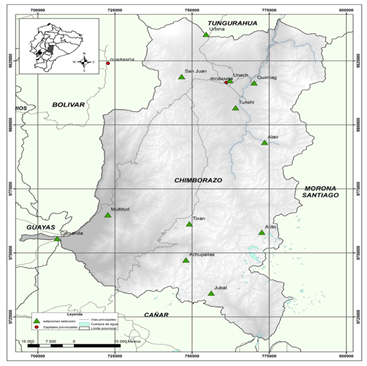
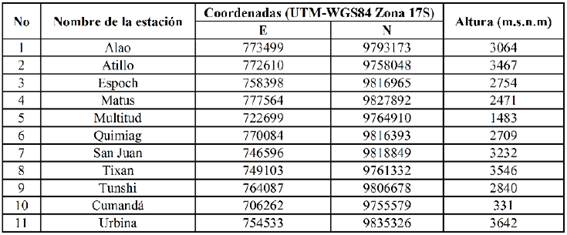
La provincia de Chimborazo está situada en la parte central de Ecuador. Su territorio se extiende en 6500 km2 desde la región trópica a 156 metros sobre el nivel del mar hasta la cima del volcán Chimborazo a 6268 m.s.n.m.13. Está atravesada por la Cordillera de los Andes y drenada por las subcuencas del río Guayas y el Pastaza. Una red de 11 estaciones meteorológicas automáticas ha sido instalada desde 2013 en toda la región. Las estaciones han medido datos como: temperatura del aire y suelo °C, humedad relativa %, presión atmosférica hPa, radiación global y difusa Wm-2, velocidad de viento ms-1. La provincia de Chimborazo posee una topografía muy variable que, en conjunto con su ubicación en el centro del país, permite la formación de 13 ecosistemas 14 y de una diversidad de microclimas en los sitios donde se encuentran distribuidas las estaciones meteorológicas, el detalle de la ubicación puede ser observado en la Figura 1.
Para este estudio se ha elegido manejar promedios diarios de temperatura del aire °C, para visualizar el comportamiento del clima en el año 2015. Esta selección tiene el 98.2% de los datos mientras que su complementario corresponde a datos faltantes. Se ha utilizado algunos modelos de transmitancia atmosférica y otros basados en imágenes satelitales creados para la zona Andina con el propósito de completar la información 10,11.
Los datos son interpretados como un sistema dinámico complejo de la evolución de las temperaturas a través del tiempo. Se considera la serie de tiempo de temperaturas en cada estación meteorológica i (i=1,2,…,n) como el estado de la variable yi (t) de un conjunto de n=11 subsistemas dinámicos posiblemente conectados, donde t representa el tiempo6. En este estudio se utiliza métodos numéricos, estadísticos y computacionales para representar el comportamiento dinámico de las temperaturas aplicando dos distintos métodos de visualización MDS y FSSP.
Análisis de escalado multidimensional (MDS)
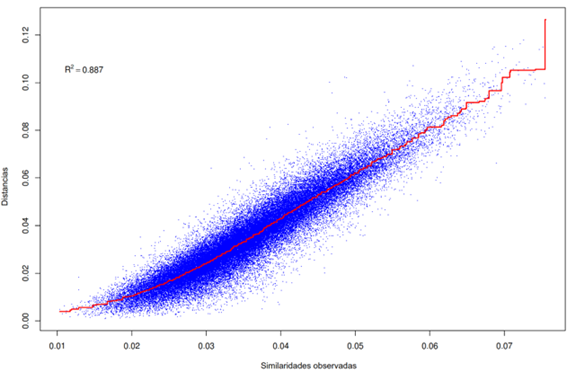
MDS es una técnica estadística utilizada para reducir la dimensión de datos multivariantes para obtener una representación espacial. Tiene una amplia aplicación en medicina, psicología, economía, geofísica y climatología 4,5,6. En este método las similitudes entre pares de objetos son representadas por las distancias Euclidianas Ecuación 1, también denominada solución clásica.
La interpretación de los resultados es la formación de conjuntos de acuerdo a la distancia entre los puntos en el mapa. Empleando software estadístico RStudio con paquetes adicionales se han generado gráficas interactivas en 2 y 3 dimensiones.
Un sistema k-dimensional se puede representar mediante un conjunto de ecuaciones diferenciales de primer orden que rigen las k variables del estado y1 (t),y2 (t),…,yk (t). Dichas ecuaciones se obtienen de la relación funcional entrada-salida del sistema para un conjunto dado de variables de estado. Conociendo y1 (t),y2 (t),…,yk (t) en el momento t≥t0 y las entradas del sistema para t≥t0. El espacio de estado consiste en el conjunto de todos los estados posibles, cada uno correspondiente a un punto único. A medida que evoluciona, obtenemos secuencias de puntos que describen trayectorias en el espacio de estados el conjunto de las trayectorias es el SSP. Para los sistemas de primero, segundo y tercer orden, se puede representar (SSP) y se puede inferir el comportamiento del sistema a partir de la correspondiente representación gráfica 5,6,15.
Se ha utilizado series de tiempo yi (t) con sus derivadas de orden entero (k-1), k Î ℝ con respecto al tiempo, que se pueden denominar variables de fase. A continuación, se puede construir el SSP. La representación k-dimensional es compleja porque el orden hipotético del modelo diferencial es desconocido. Se necesita determinar el orden óptimo de las derivadas con respecto al tiempo. Se conoce que los datos atípicos k-dimensionales son difíciles de separar en una base de datos16,17, lo cual conlleva a un trabajo exhaustivo para calcular las distancias entre cada par de variables y a la vez aplicar alguna técnica para detectar valores anómalos multivariantes. Para tal efecto, se ha aplicado diferencias numéricas para datos o funciones ruidosas, empleando el algoritmo propuesto por Holoborodko18 donde h es el periodo de muestra.
Medida de información mutua.
Como parte de la Teoría de Información se puede encontrar la definición de la Información Mutua de variables que mide la dependencia estadística mutua entre dos variables aleatorias. La Información mutua de dos variables aleatorias discretas X, Y se define como19:
Donde p(x), p(y) representan las probabilidades marginales de las variables aleatorias X,Y, además p(x,y), representa la distribución conjunta de las variables aleatorias X,Y. 6, 20. Para el presente artículo se utiliza la Información Mutua Normalizada en referencia a 21:
Donde H(X) y H(Y), representan la entropía.
La información mutua normalizada tiene la ventaja de simplificar la comparación entre diferentes condiciones y mejorar la sensibilidad.
Cálculo fraccional (CF)
El CF puede ser empleado como una extensión del Cálculo Diferencial e Integral. En la siguiente ecuación 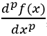 , p puede tomar cualquier valor, sea este positivo, negativo, real o imaginario; entonces se convierte en un poderoso recurso para el análisis de datos22.
, p puede tomar cualquier valor, sea este positivo, negativo, real o imaginario; entonces se convierte en un poderoso recurso para el análisis de datos22.
En este estudio se ha empleado cálculo numérico y analítico para resolver un sistema fraccional. Se menciona la ecuación diferencial de orden fraccionario en Ecuación 7.
Con condiciones iniciales yβ (0)=0 ; y(0)=0
Como una aproximación de las derivadas fraccionales de la Ecuación 5 se utiliza métodos numéricos en relación a la Ecuación 7 con el principio de “memoria a corto plazo” formulada por23
Donde L es la longitud de memoria y h es la frecuencia de tiempo.
El coeficiente binomial está dado por
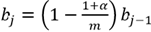 0
0Favorablemente, según23, también se puede calcular una aproximación de un sistema dinámico fraccional con sistemas de tipo entero de la siguiente manera en la Ecuación 7.
Los coeficientes de ai k del sistema dinámico de orden entero toman los siguientes valores
ai 2=0.7414; ai 1=0.2313; ai 0=1 que han sido calculados por el método de mínimos cuadrados.
Fractional state space portrait (FSSP)
Para la construcción del FSSP el orden de la derivada no se limita a un número entero, proporcionando una alternativa valiosa para obtener la representación de las relaciones entre las variables del sistema k-dimensional, visualizando características escondidas y no capturadas por otros métodos8.
Como primer paso para construir el FSSP se calcula el orden óptimo de la derivada, para el sistema dinámico6. Posteriormente se emplea las Ecuaciones 8 y 9 para obtener la representación del cambio de estado de cada variable.
Una vez obtenidas, las gráficas arrojadas por MDS y FSSP se comparan buscando la representación adecuada.
III. RESULTADOS
Análisis de Escalado Multidimensional
El conjunto de datos es representado por las mediciones de temperatura de 365 días en el año 2015 en una proyección de escalado multidimensional para u = 2 que se muestra en la Figura 2, donde cada punto representa las mediciones de la temperatura durante un tiempo t.
Las distancias cortas entre dos puntos en el mapa significan que las correspondientes mediciones son similares, mientras que las distancias largas entre los puntos representan menor similitud entre sí.
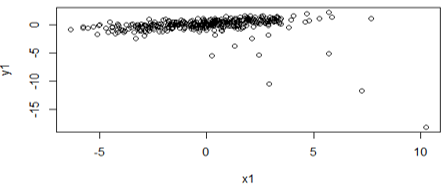
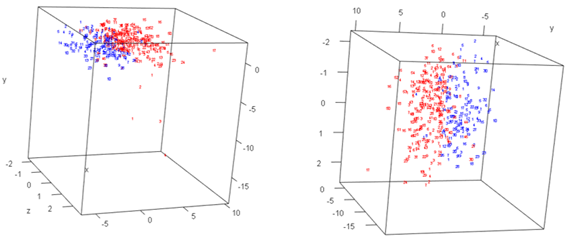
La Figura 3 muestra el escalado multidimensional para u = 3, donde se puede apreciar dos grupos semi definidos que representan las dos estaciones del año típicas de la zona ecuatorial: los días secos y lluviosos representados con puntos rojos y azules respectivamente.
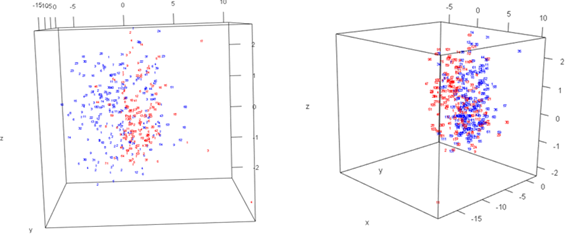
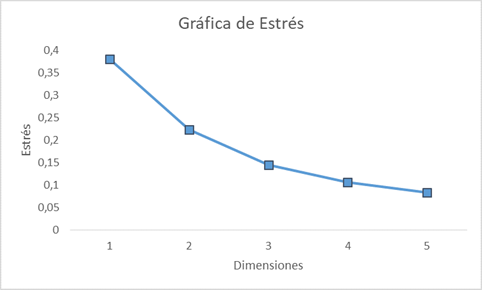
En la Figura 4 se observa el gráfico Sherpad en 2 dimensiones, donde se identifica que las similaridades y las distancias tienen una fuerte relación. El coeficiente de determinación R2=0.89, que significa que el 89% de la variabilidad de las distancias y las similaridades esta explicada. Se ha obtenido la estructura de mejor ajuste de los puntos de análisis MDS, el cual tiene el menor estrés a medida que las dimensiones aumentan como se observa en la Figura 5.
Análisis SSP
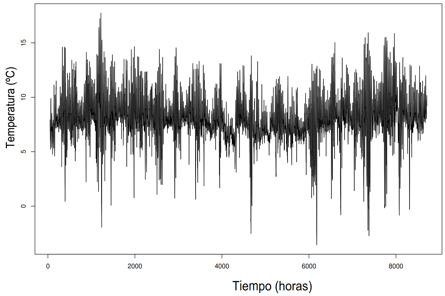
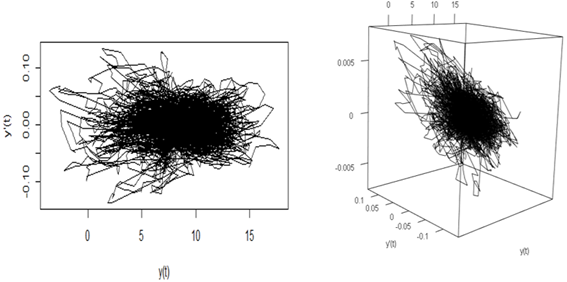
Se ha generado el SSP de la serie de tiempo de temperaturas, se observa en la Figura 6 que la variable es una serie estacionaria anual. Sin embargo utilizando las Ecuaciones 2 y 3 se puede observar el cambio de estados y(t), y'(t), y''(t) de las temperaturas plasmado en la Figura 7. La periodicidad no es evidente durante los cambios de estado representados en la gráfica.
Análisis FSSP
Para determinar el orden de las derivadas del FSSP para la ith estación meteorológica, se ha comparado s=72 valores de orden α de Dα t {yi(t)} que corresponden a discretizaciones numéricas en un intervalo de α∊0;2. Para llevar a cabo este procedimiento primero se ha calculado la Información mutua multivariante descrita por 24.
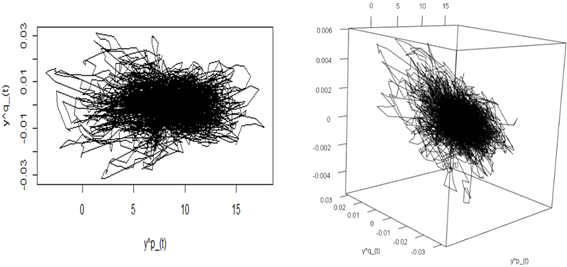
Como segundo paso se elige el orden óptimo de derivada que corresponde al mínimo valor de Ipqr(X,Y,Z), como lo sugiere Machado6. Se observa en la Figura 8 la gráfica para tres dimensiones del FSSP para el óptimo orden de derivada {αp,αq,αr }={0.02;0.70;1.52}. Los gráficos presentan una semejanza con los obtenidos empleando órdenes entero en la Figura 7.
Los grupos obtenidos por los dos métodos son aparentemente similares, sin embargo, la gráfica del FSSP (Figura 9) representa grupos de temperatura mejor definidos; de esta manera, el método FSSP se presenta como una buena alternativa para discretizar variables meteorológicas como temperaturas.
IV. DISCUSIÓN
Para la construcción del FSSP se ha obtenido el óptimo orden de derivada {αp,αq,αr} = {0.02; 0.70; 1.52} en comparación con Machado6 {αp,αq,αr} = {0.029; 0.53; 1.33}. Los valores no tienen una diferencia significativa entre sí, pero se obtiene un criterio de visualización de comportamiento de las Temperaturas.
En el mapa FSSP (Figura 9), se puede apreciar dos grupos que representan las dos estaciones del año definidas para la zona ecuatorial: los días secos en rojo y los días lluviosos en azul. Las temperaturas en climas tropicales se caracterizan por tener variaciones diarias más grandes que las variaciones anuales. Esto es típico en el Ecuador que no posee estaciones termales, además carece de un invierno largo en el cual la actividad biológica se reduzca por las temperaturas bajas. La cordillera de los Andes es el factor más influyente que genera complejos patrones espaciales de precipitación, afectadas por las cuencas del Pacífico y del Amazonas. Las masas de aire provenientes del Océano Pacífico ejercen su influencia en las laderas occidentales de la cordillera, mientras que las pendientes orientales están dominadas por corrientes de aire húmedo que provienen del Atlántico y la cuenca del Amazonas 25,26. En los valles interandinos las masas de aire oceánicas y continentales se encuentran, formando dos estaciones climáticas en la zona: días lluviosos de febrero a mayo y octubre y noviembre; días secos en el periodo de junio a septiembre, el cual es más pronunciado que el segundo periodo alrededor de diciembre 25.
La provincia de Chimborazo no se caracteriza por su uniformidad topográfica, altitudinal, ni climática. Su configuración biogeográfica hace posible la formación de 13 ecosistemas en su territorio14. La formación de microclimas con diferente precipitación y humedad relativa permite que no se observe una diferenciación muy marcada entre las estaciones, lo cual es visible en la Figura 9, donde los clústeres se encuentran muy cercanos entre sí.
V. CONCLUSIONES
Al aplicar el Análisis de Escalado Multidimiensional se ha podido identificar dos grupos no delimitados, los cuales se les ha asociado a días secos y lluviosos. La gráfica de Sherpad indica que el 89% de la variabilidad de los datos están explicados por el modelo en tres dimensiones.
Se compararon los 72 valores de orden α que corresponden a discretizaciones numéricas en un intervalo α ∊ 0,2. De la comparación se ha empleado los valores menores resultantes. Estos valores forman el orden de derivada óptimo para la construcción del FSSP. Se ha comparado con el orden de derivada entero y se ha determinado que no tienen una diferencia significativa.
La aplicación de FSSP funciona como una herramienta útil para discretizar el conjunto de datos y mejorar la representación visual del sistema dinámico. Al comparar la Figura 3 con la Figura 9, en esta última se puede observar con mayor claridad dos grupos: días secos y días lluviosos; el mejor método evaluado en el estudio para interpretar el sistema dinámico de las temperaturas de 11 estaciones meteorológicas en la provincia de Chimborazo en el año 2015 es el FSSP.