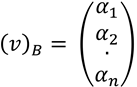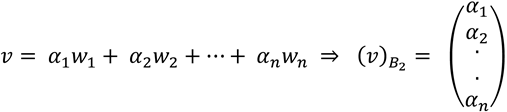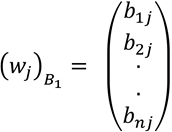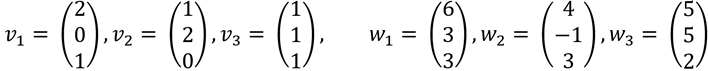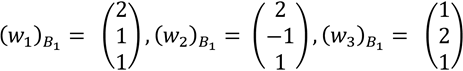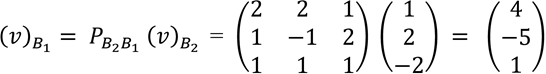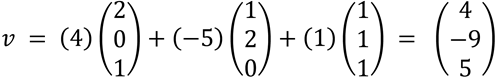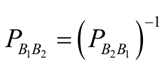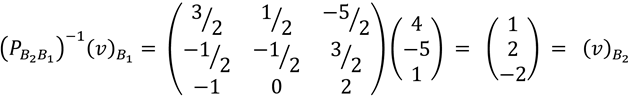LA ENSEÑANZA DEL ALGEBRA LINEAL

El Algebra Lineal actualmente es uno de los principales temas de estudio en los currículos de las Ingenierías, sin embargo, no se le presta el interés que el tema tiene. El Algebra Lineal es una rama de las matemáticas que estudia diferentes conceptos como vectores, matrices, sistemas de ecuaciones, transformaciones lineales, espacios vectoriales y las diversas propiedades que cada concepto comprenda. Dentro de los espacios vectoriales tenemos conceptos que son bastante abstractos como el de subespacio, las bases, las transformaciones lineales, los autovalores y los autovectores. El Algebra Lineal ha cobrado una mayor importancia con el desarrollo de las computadoras porque permiten hacer un número mayor de operaciones. Por lo general, la mayoría de las ciencias básicas y la computación requieren de los fundamentos que conforman el Algebra Lineal.

Una de las aplicaciones del Algebra Lineal la encontramos en el buscador Google ¹⁵, quien subraya que el éxito de Google se debe a un algoritmo llamado “Page Rank” que tiene mucho que ver con el Algebra Lineal. De igual forma el formato JPEG, de una imagen digital es una matriz, se indica en ¹⁵ que en el formato JPEG se divide la imagen en bloques 8x8 y se somete cada bloque a una transformación matricial ortogonal.

En 1997 Dubinsky ³ publicó un artículo donde advertía que las dificultades que tienen los estudiantes con los conceptos de Algebra Lineal no pueden y no deben evitarse concentrándose en los aspectos computacionales de esta materia y eludiendo la abstracción, sin embargo, es de hacer notar que el aligerar los cálculos que se deben realizar permite dedicar una mayor cantidad de tiempo al razonamiento abstracto de los problemas.

Un concepto difícil de enseñar es el de base de un Espacio Vectorial, para el cual la investigación en educación matemática le ha dedicado poca atención ³. Sin embargo, el aprendizaje de este concepto es fundamental en la estructura de los Espacios Vectoriales y se relaciona directamente con otros conceptos del Algebra Lineal como las Transformaciones Lineales.

Tratando de resaltar la dificultad que presenta el concepto de base, Oktac y Trigueros ¹¹ señalan que aun cuando los estudiantes intentan articular las propiedades del concepto de base, no son capaces de verificar cuando un conjunto es base de un Espacio Vectorial, ni de coordinar los elementos conceptuales involucrados en su construcción. Esto nos hace pensar que al introducir el concepto de cambio de base presentará una mayor complejidad la realización de los cálculos correspondientes.

Una gran cantidad de procedimientos de Algebra Lineal necesitan de cálculos largos y en algunos casos tediosos, tales como la inversa de una matriz para lo cual se usa el método de Gauss-Jordan, el cual también se puede utilizar para resolver un sistema de ecuaciones, sin embargo, para este último muchas veces, por la reducción de los cálculos, se usa el método de eliminación Gaussiana o método de Gauss. Otros procedimientos para los cual es difícil realizar las operaciones es el cálculo de autovalores y autovectores.

Por el motivo anterior es que se han desarrollado una serie de programas comerciales como MATLAB, MAPLE, DERIVE y de software libre como GEOGEBRA, SAGE, que se utilizan para aligerar los cálculos en la enseñanza de las matemáticas y que encuadran en los denominados Sistemas de Cálculo Algebraico (SCA). Sin embargo, aunque con algunos se puede reducir una matriz aplicando el método de Gauss-Jordan (DERIVE) y con otros se puede calcular el polinomio característico y los autovalores y autovectores (SAGE), ninguno de ellos tiene alguna función interna que permita el cambio de base de un Espacio Vectorial.

Las posibilidades simbólicas, numéricas y gráficas que ofrecen estos programas están provocando numerosos cambios en la enseñanza y aprendizaje de esta disciplina ⁸. Según Guzmán ⁵ el uso de los SCA en el aula permite prescindir del esfuerzo rutinario de cálculo y esto puede favorecer a que el estudiante se dedique más a la exploración y el razonamiento de los problemas matemáticos que se le presentan.

El uso de los SCA está basado en la metodología:

la construcción del conocimiento matemático por medio de la exploración y la experimentación

. Esta es una metodología basada en la adquisición de aprendizajes por medio de la experimentación, la exploración y la observación del alumno en base a unos conocimientos previos y denominada aprendizaje significativo ¹.

Una experiencia positiva ha tenido ¹² al utilizar el programa DERIVE en la enseñanza de Algebra Lineal, quien señala que el programa DERIVE ha permitido que los alumnos realicen con menos esfuerzo los cálculos repetitivos y rutinarios, así como no ha generado barreras adicionales para el aprendizaje de los principales contenidos de Algebra Lineal. Por otra parte, ¹² también señala que dicho programa ha sido un elemento motivador para el aprendizaje porque les ha facilitado el cálculo, lo cual les ha permitido llegar al final en la resolución de muchos problemas.

Nosotros hemos escogido MATLAB para el desarrollo de una función para el cálculo de la matriz del cambio de base, porque el mismo es un programa diseñado para el uso de vectores y matrices, y ha desarrollado algunos algoritmos internos que realizan los cálculos de algunos conceptos del Algebra Lineal, por ejemplo: el determinante de una matriz (det(A)), la inversa de una matriz (inv(A)), el cálculo de los autovalores y autovectores y otros.

Por otra parte, MATLAB es un programa versátil y fácil de aprender, también nos permite establecer un balance entre la teoría y la práctica. Los estudiantes pueden aprender los conceptos teóricos en el aula de clase y luego pueden implementar y probar con MATLAB los conocimientos adquiridos. Muchas de las funciones necesarias para implementar los conceptos son funciones internas del programa y pueden ser llamadas desde el script y no tienen que implementarlas ellos mismos, pero en este último caso también se pueden construir algunas funciones por la facilidad de su lenguaje dinámico de programación.

EL CONCEPTO DE CAMBIO DE BASE

El cambio de base es un concepto fundamental en la teoría de los espacios vectoriales, ya que involucra los conceptos de independencia lineal y combinación lineal. Comenzaremos viendo la definición de Espacio Vectorial , según ⁶

Sea (K,+, .) un cuerpo. Sea V un conjunto no vacío, sea “+” una operación en V y sea “.” una acción de K en V. Se dice que (V,+, .) es un K-espacio vectorial si se cumplen las siguientes condiciones:

Siguiendo al mismo autor ⁶ tenemos la definición del concepto de base

Sea V un K-espacio vectorial. Una familia 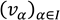se llama una base del espacio vectorial V si 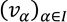es una familia linealmente independiente de V y que genera a V.

La propiedad fundamental del concepto de base es que cualquier vector del espacio vectorial se puede escribir como combinación lineal de los elementos de la base, así

Esta propiedad nos permite escribir cada uno de los vectores en función de los vectores de la base y el vector que se forma con los escalares de la combinación lineal se llama vector coordenado respecto a la base correspondiente.

De igual manera definimos lo que es la coordenada de un vector en una base determinada

Sea V un K-espacio vectorial de dimensión finita y sea 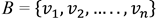una base de V. Dado v ϵ V, existen únicos tales que 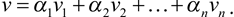. El vector 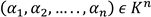se llama vector coordenadas de v en la base B y se denota por

Ejemplo 1

Sea la base 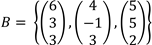y consideremos el vector 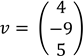al hacer la combinación lineal tenemos

Ya al saber cómo se escribe el vector coordenado respecto a una base podemos establecer la matriz del cambio de base o matriz de transición de una base a otra ⁷. Para ello supongamos que tenemos las bases 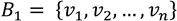y 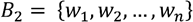del espacio n-dimensional V. Ahora consideremos un vector v ϵ V y escribimos el vector coordenado respecto a la base B₂

Entonces

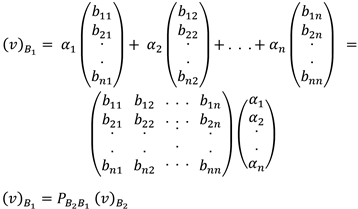
Ahora escribamos al vector w_j en las coordenadas respecto a la base B₁ como

Entonces

donde

es la matriz del cambio de la base B₂ a la base B₁.

Ejemplo 2

Sean 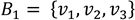y 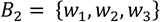bases del espacio vectorial R³, donde

Ahora calculamos la matriz de cambio de base 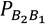, para ello buscamos el vector coordenado para cada uno de los vectores wi respecto de la base B1. Así, resolvemos el sistema de ecuaciones 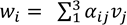para cada uno de los vectores.

Esto es

lo cual nos da los siguientes vectores coordenados

y formamos la matriz de cambio de base .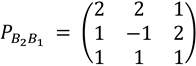

Consideremos el vector 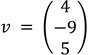, del ejemplo 1, donde sus coordenadas respecto a la base B2 es 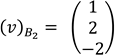y para determinar sus coordenadas respecto a la base B₁ aplicamos la ecuación señalada en (2), es decir,

Ahora podemos comprobar utilizando los vectores de la base 𝐵 1 que

De esta forma, podemos pasar de una base a la otra y viceversa, eso nos muestra que la matriz de cambio de base de la base B₁ a la base B₂ se puede construir de la misma forma o mediante la inversa de la matriz de cambo de base de la base B₂ a la base B₁. Así

Ejemplo 3

Sea la matriz de cambio de base de B₂ a B₁ del ejemplo anterior. Podemos comprobar que 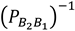es la matriz de cambio de base de B₁ a B₂, ya que

DESARROLLO DE LA FUNCIÓN CAMBIO DE BASE EN MATLAB

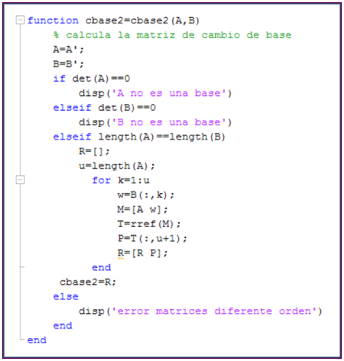
Para construir la función de cambio de base utilizamos el programa de MATLAB por la ventaja que tiene en sus funciones internas como, por ejemplo, la función “rref(A)” que permite escalonar la matriz A y la cual utilizamos para la obtención de las coordenadas de un vector respecto de una base cualquiera.

Primero veremos en la Figura 1, la rutina que presenta la función que creamos “cbase2(A,B)” que determina la matriz del cambio de base de la base A a la base B. Puesto que las matrices en MATLAB se introducen como vectores fila, debemos tener presente que las matrices que representan las bases serán introducidas en filas y en la rutina del programa se convierten a columna utilizando la transpuesta de una matriz.

Ahora utilizando las bases del ejemplo 2 establecimos la rutina correspondiente y mostramos los resultados en MATLAB, en donde introducimos la matriz 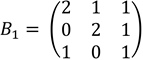denotada por B₁ y la matriz 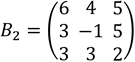denotada por B₂, calculamos la matriz del cambio de base de B₂ a B₁ denotada por P21, como se ve en la Figura 2.

Introducimos el vector 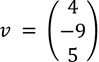y calculamos las componentes del vector v respecto a la base B₂, 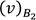que denotamos por C2 y las componentes del vector v respecto a la base B₁, 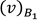que denotamos por E2. Luego multiplicamos la matriz P21 por el vector C2 y vemos que el resultado, indicado con W, es el vector E2, como debería de ser el resultado; de igual forma para comprobar el resultado multiplicamos la matriz de la base B₁ por el vector resultante W y obtenemos nuestro vector original v.

Para mostrar la utilidad con matrices de mayor orden, consideremos las bases B₁ y B₂ de R⁵ mostradas en la Figura 3 del ejemplo 4 y calculamos la matriz de cambio de base de B₁ a B₂ que denotamos con P12, utilizando la función desarrollada, y vemos que sin ningún problema MATLAB calcula una matriz de cambio de base P12 de dimensión 5x5.

Ejemplo 4

De igual forma, vemos que la función opera con bases de números complejos, ya que MATLAB permite las operaciones con dichos números dentro de su estructura matricial.

En el ejemplo 5 consideraremos dos bases C1 y C2 con elementos dentro del campo de los números complejos (₵). Calculamos la matriz de cambio de base de C2 a C1 y la denotamos por P21 y vemos que tenemos una matriz 3x3 con valores complejos. Para comprobar el resultado tomamos un vector A en la base C1 y aplicamos la matriz P21 para obtener el vector K en la base C2.

Luego buscamos la inversa de P21, según ³, que es la matriz del cambio de base de C1 a C2 y al multiplicar la inversa por el vector K obtenemos el vector L que es el mismo vector A. Con esto se comprueba que la función “cbase2” también trabaja dentro del campo de los números complejos.

Ejemplo 5