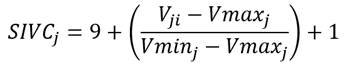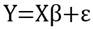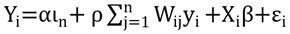Introducción
En la literatura sobre el desarrollo regional, la competitividad regional está asociada con el conjunto de capacidades y potencialidades internas y externas que poseen los territorios y que son utilizados como instrumentos públicos o privados de desarrollo territorial integral. En América Latina se han evidenciado avances significativos en la competitividad en los últimos años, sin embargo el desarrollo se ha concentrado en pocos países o regiones (Mortimore & Pérez, 2001). La transformación de los regímenes económicos iniciada en la década de 1980 en varios países latinoamericanos ha dejado en evidencia que la apertura de los mercados no ha bastado para fomentar la competitividad interna y producir un crecimiento económico con una mejora en la distribución del ingreso y los niveles de vida (Helmsing 2001). La necesidad de diseñar instrumentos y políticas encaminadas a aprovechar las potencialidades del territorio para fomentar el desarrollo regional basado en las características económicas regionales, requiere de mayor análisis a la luz de nuevos datos (Silva 2005).
En el caso de Ecuador, existe un comportamiento similar. Si bien el país ha presentado mejoras en sus niveles de competitividad nacional, existe un alto grado de desigualdad regional, los beneficios del desarrollo se han concentrado en pocos territorios y en los deciles de mayor ingreso (Alvarado, 2011; Mendieta-Muñoz y Pontarollo, 2018; Jiménez y Alvarado, 2018a). En este sentido, la competitividad ha sido analizada no únicamente a nivel nacional sino también con enfoque regional, puesto que las disparidades presentadas a nivel territorial no podrán ser enfrentadas si no se toman en cuenta las debilidades de las economías de sus regiones (Ochoa & Celi, 2012). La lógica subyacente de utilizar datos territoriales y no datos nacionales se debe a que el desarrollo económico y social no es homogéneo en el territorio, en particular, en el caso de Ecuador, las disparidades territoriales son muy significativas (Jiménez, & Alvarado, 2018a; Jiménez & Alvarado, 2018b; Huachizaca & Alvarado, 2018). En consecuencia, dichas disparidades o desigualdades deben ser consideradas en el diseño y aplicación de políticas públicas para integrar a todos los territorios al proceso de desarrollo. En consecuencia, en nuestra investigación, el desarrollo regional o territorial es una referencia a la incorporación del territorio al análisis económico, específicamente utilizamos la escala cantonal con datos para los 224 cantones de Ecuador.
Existe una diversidad de conceptos y técnicas que se han desarrollado para medir la competitividad. En el caso ecuatoriano se han calculado índices de competitividad provincial (Alvarado, 2011), y la literatura a nivel cantonal aún es escasa. La mayor disponibilidad de datos de las Cuentas Nacionales y los Censos Económico y de Población y Vivienda del 2010 facilitan la construcción del índice a escala más pequeña y con un mayor número de variables, que permita la modelación econométrica más consistente. Además, la creciente literatura teórica y empírica al respecto (Schwab, 2014; IMD, 2008; Huggins & Davies, 2006) constituye un marco referencial que facilita el análisis y comprensión de las causas del desarrollo regional, que en parte, puede tener diferentes causas que el desarrollo nacional.
El problema que investiga este trabajo tiene dos dimensiones. Primero, aborda la falta de investigaciones sobre la competitividad a escala cantonal. Segundo, analizamos la disparidad cantonal en cuanto a la competitividad como un indicador más amplio del desarrollo territorial. Bajo este contexto, es necesario analizar cuál es el nivel de competitividad de los cantones de Ecuador y cuál es la influencia de los niveles de competitividad en el desarrollo regional de los cantones del Ecuador. Nuestra hipótesis es que a nivel cantonal existe disparidad en cuanto a la competitividad y que la competitividad tiene un efecto positivo en la productividad, el ingreso per cápita y valor agregado, y una relación negativa con la pobreza. En resumen, esta investigación construye un índice de competitividad cantonal para Ecuador usando datos de fuentes secundarias. En la segunda etapa, se examina la correlación entre el desarrollo regional y el índice de competitividad cantonal usando modelos de econometría espacial.
El resto del artículo tiene la siguiente estructura: la segunda sección describe el sustento teórico y la evidencia empírica; la tercera describe los datos, la metodología del índice de competitividad regional y el planteamiento de los modelos econométricos; en la cuarta sección se discuten los resultados encontrados y finalmente, en la quinta sección constan las conclusiones e implicaciones de política derivados de la investigación.
Revisión de la literatura previa
La competitividad, en los diferentes niveles territoriales tiene sus raíces en los trabajos de la gestión estratégica, de economía industrial y la teoría del comercio. En este sentido, podemos citar a Schumpeter (1950) y Porter (1981), quienes han extendido la literatura de competitividad a nivel territorial y regional medida a partir de la ventaja competitiva estratégica de las empresas e industrias. Autores como Martin, Kitson & Tyler (2006) señalan que hay una diferencia importante entre la evolución de las empresas y las regiones, puesto que las empresas entran y salen de los mercados, en contraste con las regiones que son fijas. Bajo la misma línea de investigación, Asheim (1996), Cooke et al. (1998), Cooke (2001) y Storper (1997) indican que para alcanzar una competencia básica de los territorios es necesario que las regiones cuenten con factores de forma integral, tales como los factores sociales, culturales e institucionales, los cuales son relevantes para fomentar el desarrollo económico de forma integral y no de forma aislada. En este sentido, las inversiones públicas o privadas de forma aislada no necesariamente generan desarrollo debido a que su impacto positivo se diluye por las desventajas de los territorios o al menos, el efecto positivo de las inversiones aisladas es pequeño que se pierde con el paso del tiempo.
En la práctica, existen diferentes problemas teóricos y conceptuales en cuanto a la competitividad en sus distintos niveles espaciales, lo que a su vez dificulta la medición. Existen publicaciones de estudios con un fuerte componente cuantitativo que aplican métodos específicos para la medición del nivel de competitividad (Annoni & Kozovska, 2010). Uno de los aportes teóricos más utilizados es el realizado por el Foro Económico Mundial (Schwab, 2014), el cual considera en el cálculo del índice de competitividad 12 pilares, entre los cuales constan: instituciones, infraestructura, macroeconomía, salud y educación primaria, educación y formación superior, eficiencia del mercado de bienes, eficiencia del mercado de trabajo, sofisticación del mercado financiero, preparación tecnológica, tamaño del mercado, sofisticación de los negocios e innovación.
En la literatura empírica, Pastor (2014) realizó un estudio para medir la competitividad de 24 regiones del Perú, encontrando que las regiones más competitivas son aquellas que presentan un mayor crecimiento en las variables relacionadas con el entorno económico, laboral, educación, salud, infraestructura, e institucional. En este sentido, el progreso en las condiciones básicas podría aumentar la competitividad de la economía de los departamentos con un nivel de desarrollo relativamente bajo, y por el contrario, para los departamentos con un nivel de desarrollo relativamente alto, la estrategia se debería enfocar (sin descuidar los demás factores) en acciones que les permitan sofisticar y diversificar su economía. Un estudio realizado por Olivares (2012) en Chile, determinó que la variación en el índice de competitividad regional es el resultado de las diferencias en las condiciones estructurales de cada región. Asimismo, entre otros estudios desarrollados en la región, el Instituto Mexicano para la Competitividad (IMCO, 2012) demuestra que el nivel de competitividad de ese país está en deterioro debido a la caída de los indicadores relacionados con el aspecto institucional, ambiental, económico, y social, lo que a su vez no permite atraer ni talento ni inversión a las regiones periféricas.
Para el caso de Ecuador, Alvarado (2011) encontró que las provincias más competitivas son las que cuentan con mayor concentración económica, y que por el contrario los menos competitivos son los que cuentan con baja concentración económica. Este resultado encontrado a nivel provincial, confirma que la disparidad territorial es una realidad que puede estar limitando el desarrollo del país y que requiere mayor atención en el ámbito político y académico.
El Programa de las Naciones Unidas para el Desarrollo (PNUD, 2008) determinó que la competitividad en Croacia está determinada por las características del mercado empresarial, por lo que resulta fundamental analizar la heterogeneidad del ambiente empresarial para impulsar la competitividad del territorio. Bronisz, Heijman & Miszczuk (2008) realizaron una investigación en Polonia y llegaron a la conclusión de que el nivel de competitividad regional depende principalmente de la calidad del capital humano, innovación, el conocimiento y la eficiencia de la economía regional. So & Shen (2004) evaluaron la competitividad de las 215 ciudades chinas, utilizando indicadores económicos, sociales y ambientales; y muestran que la competitividad económica o social no asegura necesariamente la competitividad medioambiental. Mientras que Du et al. (2014), mediante la metodología del análisis espacial, evidenciaron que la desigualdad espacial en términos de competitividad urbana, disminuye cuando se controla las políticas de desarrollo urbano y planificación. La competitividad urbana ayuda al desarrollo regional mediante el mejoramiento de la productividad interna de los territorios.
Fuentes estadísticas y metodología
3.1 Índice de Competitividad Regional (ICR)
A pesar de que nuestra investigación utiliza una metodología propuesta por el Foro Económico Mundial-FEM, al conjunto de variables fueron incluidas 7 dimensiones debido a una limitación en los datos, en particular en lo relacionado con la estructura productiva nacional, aspectos macroeconómicos e institucionales que solo se dispone datos a nivel nacional. Esto implica que la estructura para el análisis del índice de competitividad regional (ICR) está basada en 7 de los 12 pilares sugeridos por el Foro Económico Mundial (Schwab, 2014), e incluye a 105 variables, las cuales se organizan de la siguiente forma:
Institucional: Comprende las variables relacionadas con los trabajadores estatales; seguro social; registros de los contribuyentes; empresas con deuda formal e informal, y con déficit de financiamiento; empresas que cuentan con registros contables y tienen naturaleza jurídica; e inscripciones en el registro civil.
Infraestructura: Incluye las variables de calidad de infraestructura de servicios básicos, viviendas y carreteras.
Agregados económicos: Toma en cuenta las variables de inversión y gasto de las entidades económicas, el consumo intermedio per cápita, así como también las personas desempleadas.
Salud y educación: Integra las variables de prevalencia de discapacidades, disponibilidad de programas de aprendizaje, educación primaria, personas con idioma extranjero, analfabetismo, asistencia a centros de enseñanza regular, educación secundaria y educación superior.
Empresas y Laboral: Contiene variables relacionadas con comercio al por mayor, existencias de las entidades económicas, participación de las entidades económicas en los distintos sectores del país, participación femenina en la fuerza laboral, personal remunerado, grandes empresas, establecimientos que cuentan con investigación de mercado y variables relacionadas con desarrollo empresarial.
Tecnología: Incorpora las variables relacionadas a disponibilidad de internet a nivel personal, de hogares y empresarial; gasto en I + D; disponibilidad de recursos humanos con capacidad para realizar innovación; presencia de laboratorios de I + D; y la absorción de tecnología a nivel de hogar.
Tamaño de mercado: Considera a las variables de ingresos de entidades económicas, empresas exportadoras, número de habitantes, y emigración.
Los datos de las variables utilizadas dentro del índice de competitividad regional están relativizados o normalizados, con el fin de hacer posible la comparación de los valores del índice entre los cantones. Este proceso es explicado en la metodología y datos. La información estadística es tomada del Censo de Población y Vivienda (2010), Censo Económico (2010), y Cuentas Nacionales, los cuales son elaborados y publicados por el Instituto Nacional de Estadísticas y Censos del Ecuador (INEC) y Banco Central del Ecuador, respectivamente. La falta de datos condiciona la selección de variables dentro de las dimensiones y de las variables dentro de las dimensiones. Resulta evidente que algunas variables solo se disponen a nivel nacional, tales como la tasa de interés, exportaciones, importaciones, entre otras. Sin embargo, en términos de cantidad de variables, el ICR incluye una cantidad mayor de variables que el índice a nivel nacional.
Definición de variables
La Tabla 1 presenta las variables, la descripción y la abreviatura. La variable dependiente es el desarrollo regional medido por cuatro indicadores tradicionales del desarrollo. Las variables: valor agregado bruto, productividad e ingreso per cápita son ampliamente utilizadas como medidas de desarrollo, tanto a nivel nacional como a escala regional. Mientras que los bajos niveles de pobreza también pueden ser utilizado como un indicador de desarrollo porque indica que la sociedad puede ofrecer las condiciones de vida elementales para que las personas tengan un nivel de vida básico. La variable independiente es el ICR. Finalmente, las variables de control capturan un conjunto de dotaciones de los territorios.
Tabla 1. Descripción de variables de los modelos
| Variables | Descripción | Abreviatura | ||
| Variables dependientes: | ||||
| Valor agregado bruto | Contiene la suma de los valores agregados de los sectores de agricultura, industrias y servicios. El valor agregado se obtiene de la diferencia entre lo producido por el PIB y los impuestos pagados por los mismos. | VAB | ||
| Pobreza por NBI | Número de personas que viven en condiciones de pobreza (no satisfacen sus necesidades básicas de: salud, educación, vivienda y empleo), expresadas como porcentaje del total de la población en un determinado año (SIISE, 2010). | PNBI | ||
| Productividad | Representa el ingreso de las entidades económicas en relación con el personal ocupado, en cada cantón. | PTD | ||
| Ingreso per cápita | Corresponde a los ingresos percibidos por las entidades económicas en referencia al total de población de cada cantón. | YPC | ||
| Variable independiente: | ||||
| Índice de competitividad regional | Representa la capacidad que tiene una región para competir con sus pares, calculado en base a la metodología propuesta por el Foro Económico Mundial (2014). | ICR | ||
| Variables de control | ||||
| Variables de capital humano | Porcentaje de la población que asisten a la educación primaria, secundaria, superior/postgrado, analfabetismo. | VC | ||
| Empleo | Personas con empleo formal. | |||
| Número de empresas | Número de empresas en cada cantón. | |||
| Gasto en I&D y Capacitación | Porcentaje del monto gastado en I&D y capacitación y formación. | |||
| Ruralidad | Porcentaje de población rural. | |||
| Urbanización | Tasa de urbanización cantonal. | |||
| Cercanía al mar | Variable dummy para los cantones con acceso al mar. | |||
| Polos de desarrollo | Variable dummy para Quito, Guayaquil y Cuenca. | |||
| Ingenieros, profesionales científicos e intelectuales. | Porcentaje de Ingenieros, profesionales científicos e intelectuales del total de la población cantonal. | |||
Estrategia econométrica
El índice de competitividad propuesto por Schwab (2014) del Foro Económico Mundial tiene algunas ventajas frente a los indicadores tradicionales de desarrollo. Primero, el ICR captura un conjunto de capacidades y potencialidades que incluye varias dimensiones que omiten los índices simples como el Producto Interno Bruto o Índice de Desarrollo Humano. Segundo, el ICR permite incorporar una gran cantidad de variables que capturan las capacidades de forma integral en función de la disponibilidad de datos. Finalmente, en el contexto ecuatoriano, la disponibilidad de datos generados en el Censo de Población, Censo Económico publicados por el Instituto Ecuatoriano de Estadísticas y Censos-INEC y las Cuentas Nacionales difundidas por el Banco Central facilita la disponibilidad de datos territoriales, lo cual permite obtener un ICR como un indicador adecuado de las capacidades de los cantones. Investigaciones similares recientes han ampliado la metodología del Foro Económico Mundial para incorporar la mayor cantidad posible de variables (Amate & Guarnido, 2011; Kosacoff, 2005; Pastor, 2014). La cantidad de variables en cada investigación difiere en función de la disponibilidad de datos. En el caso de Ecuador, el ICR estará compuesto por 7 sub índices (dimensiones) y estos a su vez, los índices contienen a las variables. Cada dimensión tiene el mismo peso en el indicador y cada variable tiene el mismo peso en las dimensiones. Si bien existen variables que pueden ser más importantes para generar desarrollo de los cantones, los pesos fueron estandarizados para que cada variable tenga el mismo peso relativo dentro de cada dimensión. Las razones de esta estandarización es que algunas variables pueden tener distintos niveles de importancia para los diferentes cantones, existen variables que no disponen todos los cantones (capital del país, cercanía al mar, polos de desarrollo…) y los pesos pueden ser subjetivos. De este modo, siguiendo la metodología propuesta por el Foro Económico Mundial (FEM), el cálculo del ICR parte de la siguiente fórmula:
En donde ICR i es el índice de competitividad del cantón i que captura cada dimensión de la competitividad, el término 𝑆𝐼𝐶𝑃 𝑓 es el sub índice del pilar f por cantón i. De igual manera, el sub índice de cada pilar se obtiene así:
Donde j representa las variables que contiene cada pilar. Por lo tanto, el ICR será el resultado del promedio de los sub índices de los pilares (2) y este último de los sub índices de las variables (4), de la siguiente manera:
Donde 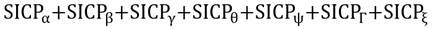 representa los sub índices de los pilares institucional, infraestructura, agregados macroeconómicos, salud y educación, empresa y laboral, tecnología y mercado, respectivamente. Y para el sub índice de competitividad de cada pilar (el cual vendría a ser el subíndice del cantón i en la variable j y este dividido para el total de variables contenidas en cada pilar), se obtiene el SIVC de las variables respectivas de la siguiente forma como lo formaliza la Ecuación 4:
representa los sub índices de los pilares institucional, infraestructura, agregados macroeconómicos, salud y educación, empresa y laboral, tecnología y mercado, respectivamente. Y para el sub índice de competitividad de cada pilar (el cual vendría a ser el subíndice del cantón i en la variable j y este dividido para el total de variables contenidas en cada pilar), se obtiene el SIVC de las variables respectivas de la siguiente forma como lo formaliza la Ecuación 4:
Donde  y
y 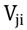 es el sub índice de la variable j del cantón i y variable j del cantón i respectivamente. Además
es el sub índice de la variable j del cantón i y variable j del cantón i respectivamente. Además 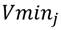 representa la variable con valor mínimo de los cantones 1, …, 221 de la variable j y Vmaxj representa la variable con valor máximo de los cantones 1, …, 221 de la variable j. Si SIVCj = 10, indica que el cantón i tiene la mayor competitividad en esa variable j y así continua de forma descendente hasta que si SIVCj = 1, el cual indica que el cantón i tiene la menor competitividad en esa variable j. Finalmente, para las variables donde el menor valor presentado indica una ventaja para el cantón, se aplica la Ecuación 5. Asimismo, existe una amplia literatura teórica y empírica que demuestra que los valores que toman las variables, dependen de los valores de las variables en los territorios vecinos (LeSage & Pace, 2009). En el caso de Ecuador, varias variables económicas y sociales siguen procesos de dependencia espacial (Jiménez & Alvarado, 2018a; Jiménez & Alvarado, 2018b). En la literatura sobre la competitividad regional no existen teorías consolidadas que fundamenten el rol de la competitividad y su efecto en el desarrollo regional. Sin embargo, los trabajos empíricos a escala regional se han incrementado como una forma de territorializar el enfoque nacional planteado por el Foro Económico Mundial. Para construir el modelo de dependencia espacial, en la formalización partimos de una ecuación tradicional (MCO) en forma matricial:
representa la variable con valor mínimo de los cantones 1, …, 221 de la variable j y Vmaxj representa la variable con valor máximo de los cantones 1, …, 221 de la variable j. Si SIVCj = 10, indica que el cantón i tiene la mayor competitividad en esa variable j y así continua de forma descendente hasta que si SIVCj = 1, el cual indica que el cantón i tiene la menor competitividad en esa variable j. Finalmente, para las variables donde el menor valor presentado indica una ventaja para el cantón, se aplica la Ecuación 5. Asimismo, existe una amplia literatura teórica y empírica que demuestra que los valores que toman las variables, dependen de los valores de las variables en los territorios vecinos (LeSage & Pace, 2009). En el caso de Ecuador, varias variables económicas y sociales siguen procesos de dependencia espacial (Jiménez & Alvarado, 2018a; Jiménez & Alvarado, 2018b). En la literatura sobre la competitividad regional no existen teorías consolidadas que fundamenten el rol de la competitividad y su efecto en el desarrollo regional. Sin embargo, los trabajos empíricos a escala regional se han incrementado como una forma de territorializar el enfoque nacional planteado por el Foro Económico Mundial. Para construir el modelo de dependencia espacial, en la formalización partimos de una ecuación tradicional (MCO) en forma matricial:
Donde 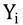 es la variable dependiente. En nuestra investigación, la variable dependiente que mide el desarrollo regional, está representado por cuatro variables que miden el desarrollo de cada cantón: Valor agregado bruto per cápita, productividad regional, ingreso per cápita y tasa de pobreza. En el caso de las tres primeras variables, mientras más altos sean los valores de las variables indican mayor desarrollo cantonal, mientras que, con respecto a la tasa de pobreza, mientras más baja, indica mayor desarrollo cantonal. De ahí el planteamiento de las hipótesis de la investigación. Los indicadores de desarrollo más utilizados son el producto per cápita o el índice de desarrollo regional. Con el fin de conseguir mayor generalidad de los resultados, incluimos otros indicadores alternativos del desarrollo regional, específicamente incluimos variables similares de desarrollo (valor agregado bruto per cápita y productividad regional). Además, a medida que una región se desarrolla, genera las condiciones para que la pobreza se reduzca. En este sentido, cuando la tasa de pobreza es baja, es un indicador de que la región a alcanzado un desarrollo alto. Asimismo, cada observación tiene una media de
es la variable dependiente. En nuestra investigación, la variable dependiente que mide el desarrollo regional, está representado por cuatro variables que miden el desarrollo de cada cantón: Valor agregado bruto per cápita, productividad regional, ingreso per cápita y tasa de pobreza. En el caso de las tres primeras variables, mientras más altos sean los valores de las variables indican mayor desarrollo cantonal, mientras que, con respecto a la tasa de pobreza, mientras más baja, indica mayor desarrollo cantonal. De ahí el planteamiento de las hipótesis de la investigación. Los indicadores de desarrollo más utilizados son el producto per cápita o el índice de desarrollo regional. Con el fin de conseguir mayor generalidad de los resultados, incluimos otros indicadores alternativos del desarrollo regional, específicamente incluimos variables similares de desarrollo (valor agregado bruto per cápita y productividad regional). Además, a medida que una región se desarrolla, genera las condiciones para que la pobreza se reduzca. En este sentido, cuando la tasa de pobreza es baja, es un indicador de que la región a alcanzado un desarrollo alto. Asimismo, cada observación tiene una media de  y un componente aleatorio
y un componente aleatorio  . El término
. El término 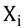 contiene al ICR y al conjunto de variables de control indicados en la Tabla 1. Sin embargo, este modelo no toma en cuenta la dependencia espacial, por lo que es necesario incluir la dependencia espacial para evitar el sesgo por omisión de variables relevantes. Para corregir el potencial sesgo que puede provocar la omisión de la dependencia espacial, Ord (1975) propuso una parametrización parsimoniosa para las relaciones de dependencia entre las variables, la cual se basa en principios de Whittle (1954). Esta estructura lleva a un proceso de generación de datos conocido como un proceso autorregresivo espacial. La Ecuación 7 captura el proceso autorregresivo, donde se incorpora el subíndice i para indicar a cada cantón:
contiene al ICR y al conjunto de variables de control indicados en la Tabla 1. Sin embargo, este modelo no toma en cuenta la dependencia espacial, por lo que es necesario incluir la dependencia espacial para evitar el sesgo por omisión de variables relevantes. Para corregir el potencial sesgo que puede provocar la omisión de la dependencia espacial, Ord (1975) propuso una parametrización parsimoniosa para las relaciones de dependencia entre las variables, la cual se basa en principios de Whittle (1954). Esta estructura lleva a un proceso de generación de datos conocido como un proceso autorregresivo espacial. La Ecuación 7 captura el proceso autorregresivo, donde se incorpora el subíndice i para indicar a cada cantón:
Dónde, 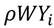 es el rezago espacial, construido a partir de observaciones de las regiones que son vecinas a las observaciones de la región i; W representa la matriz estandarizada de pesos espaciales de primer orden, donde cada vecino de un cantón tiene un peso idéntico. Los resultados no sufren alteraciones si la matriz de pesos espaciales generados mediante la contigüidad es reemplazada por una matriz de distancia por carretera. Incorporando el término constante, el modelo básico a estimar se formaliza en la Ecuación 8:
es el rezago espacial, construido a partir de observaciones de las regiones que son vecinas a las observaciones de la región i; W representa la matriz estandarizada de pesos espaciales de primer orden, donde cada vecino de un cantón tiene un peso idéntico. Los resultados no sufren alteraciones si la matriz de pesos espaciales generados mediante la contigüidad es reemplazada por una matriz de distancia por carretera. Incorporando el término constante, el modelo básico a estimar se formaliza en la Ecuación 8:
En la práctica, la Ecuación 8 puede cambiar si el diagnóstico de dependencia espacial indica que el error espacial puede contribuir a la explicación del desarrollo de los cantones. De ser el caso, se incluye el parámetro  y se asume que el parámetro
y se asume que el parámetro 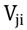 es igual a cero. La elección entre un modelo de rezago espacial (SAR), un modelo de error espacial (SEM) o un modelo mixto (SARMA), está condicionado a los resultados del test de dependencia espacial (Anselin & Bera 1998). El I-Moran señala la existencia de dependencia espacial, por lo que la inclusión del territorio en la comprensión del desarrollo cantonal está justificada por el comportamiento de los datos.
es igual a cero. La elección entre un modelo de rezago espacial (SAR), un modelo de error espacial (SEM) o un modelo mixto (SARMA), está condicionado a los resultados del test de dependencia espacial (Anselin & Bera 1998). El I-Moran señala la existencia de dependencia espacial, por lo que la inclusión del territorio en la comprensión del desarrollo cantonal está justificada por el comportamiento de los datos.
Resultados y discusión
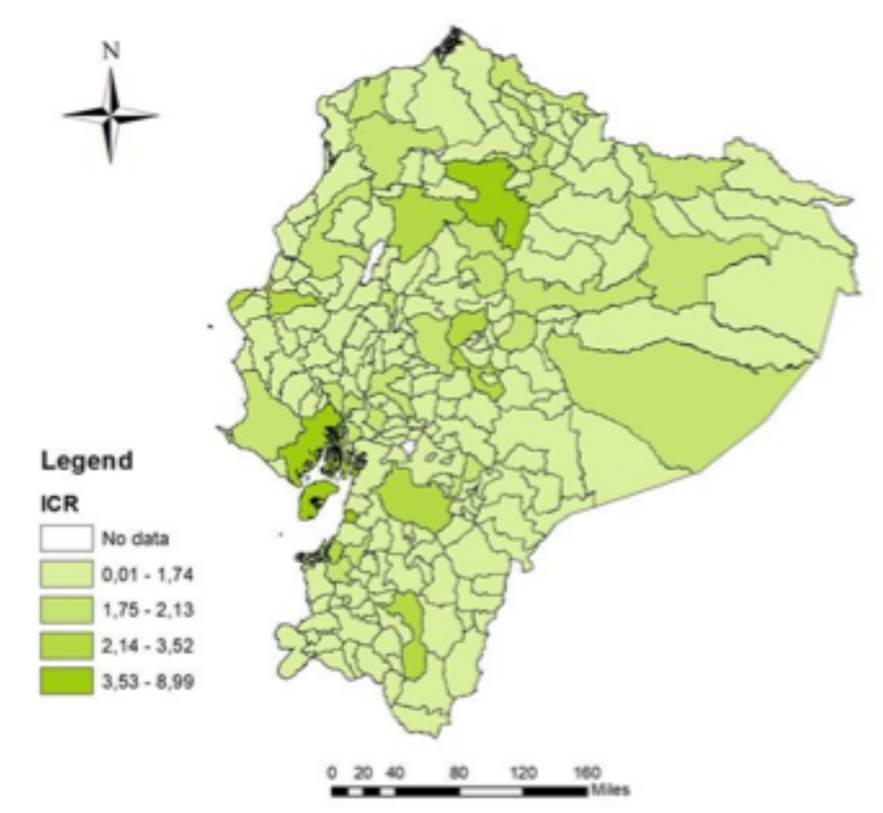
En este apartado presenta los índices de competitividad regional (ICR) de los 221 cantones del país usando un mapa degradado, donde los colores más intensos indican mayores valores del ICR y viceversa. Se puede observar que únicamente 8 cantones son los que presentan mayor competitividad, llegando a un valor del ICR de aproximadamente entre 5.7 y 6.0. Entre estos cantones están Quito, Rumiñahui, Samborondón, Guayaquil y Cuenca los cuales cuentan con mayor movimiento económico y con mejor estándar de calidad en infraestructura, salud y educación. El caso del cantón Rumiñahui puede estar explicado por la cercanía con Quito y su posible contagio espacial.
Estos resultados concuerdan con los resultados de Pastor (2014) y Alvarado (2011), los cuales establecen que las regiones con mayor competitividad son aquellas que han liderado en los pilares económicos, de infraestructura y de salud. De igual manera otros autores como Bronisz, Heijman & Miszczuk (2008), concluyen que para presentar mayores niveles de competitividad regional es necesario también contar con mayor calidad del capital humano, innovación y conocimiento. Asimismo, se tiene que los 3 cantones pertenecientes a la provincia de Galápagos: San Cristóbal, Santa Cruz e Isabela ocupan también los primeros puestos de competitividad; siendo casos especiales ya que, aunque no cuentan con el mayor subíndice en todos los 7 pilares o dimensiones.
En el siguiente rango se encuentran los cantones de Loja, Machala, Ibarra, Durán entre otros 37 cantones, los cuales están condicionados por los pilares de infraestructura, de salud y educación. Dentro de este grupo también se encuentran los cantones Salinas, Baños, La Libertad, Santo Domingo entre otros. Los factores como el turismo hacen que la mayor parte de su población se encuentre empleada y que por lo tanto se genere mayores ingresos para esos cantones. Y entre los menos competitivos, con un rango de entre 3.15 y 4.05, están los cantones de Yacuambi, Quinsaloma, Logroño entre otros 42 cantones; debido principalmente a que no cuentan con un buen estado de la infraestructura, el acceso a salud y educación es baja, y tienen un tamaño de mercado reducido.
Una vez obtenido el ICR, se determina la relación competitividad-desarrollo, para lo cual inicialmente se presenta las estimaciones mediante un modelo de Mínimos Cuadrados Ordinarios (MCO) en la Tabla 2. El efecto del índice de competitividad regional en las cuatro medidas del desarrollo regional tiene un efecto significativo al 5%. El cambio en el VAB y en el ingreso pe cápita cantonal es extremadamente similar cuando cambia el ICR, mientras que el cambio en la productividad es menor. Asimismo, el resultado obtenido en cuanto a la pobreza cantonal, se puede inferir que la competitividad cantonal es clave para reducir la pobreza.
Tabla 2. Resultados de la relación desarrollo cantonal-ICR mediante MCO
| VAB | PNBI | PTD | YPC | |
| Índice de competitividad regional | 1.600*** | -0.352*** | 0.709*** | 1.595*** |
| (8.95) | (-19.67) | (8.15) | (15.83) | |
| Constante | 3.249*** | 6.023*** | 6.529*** | -0.434 |
| (3.72) | (68.99) | (15.36) | (-0.88) | |
| Observaciones | 221 | 221 | 221 | 221 |
| R2 Ajustado | 0.264 | 0.637 | 0.229 | 0.532 |
A pesar de la coherencia de los resultados de correlación presentados en la Tabla 2, es posible que estén sesgados por la omisión de variable relevante, específicamente por la omisión del rol del espacio en la comprensión del desarrollo económico. En este sentido, es necesario utilizar una prueba formal de dependencia espacial y verificar si existen patrones de dependencia en las variables debido a la interacción entre los territorios (LeSage & Pace, 2009). La interacción entre los territorios pude ser mediante los flujos de comercio, capitales, conmutación, migración, transporte, u otras (Jiménez y Alvarado, 2018a; Jiménez y Alvarado, 2018b). La Tabla 3 reporta los resultados del diagnóstico de dependencia espacial del Multiplicador de Lagrange, el cual es utilizado para determinar el tipo de modelo que debe ser estimado. La prueba es estimada para las cuatro variables dependientes: VAB, pobreza, productividad e ingreso per cápita. Los resultados del Multiplicador de Lagrange sugieren que la variable pobreza tiene patrones espaciales, tanto con la prueba normal y robusta, específicamente, en el rezago espacial y de error espacial de forma combinada. En la práctica, los resultados sugieren que se debe estimar un modelo SARMA.
Tabla 3. Resultados del diagnóstico de dependencia espacial
| Prueba | VAB | Pobreza | Productividad | Ingresos per cápita |
| Lagrange Multiplier (lag) | 1.15 | 23.98*** | 0.89 | 0.33 |
| Robust LM (lag) | 0.73 | 12.63*** | 0.04 | 0.76 |
| Lagrange Multiplier (error) | 1.55 | 11.48*** | 0.86 | 0.07 |
| Robust LM (error) | 1.14 | 0.13 | 0.00 | 0.49 |
| Lagrange Multiplier (SARMA) | 2.29 | 24.12*** | 0.90 | 0.83 |
La Tabla 4 reporta los resultados de línea de base de la relación entre la pobreza regional y el índice de competitividad regional. Los resultados de las tres variables dependientes adicionales son omitidos debido a que los resultados del diagnóstico de dependencia espacial sugieren que, en estas variables, no existen patrones o regímenes espaciales con un nivel de significancia del 5%. Por lo tanto, el resto de regresiones estimadas y reportadas son usando la tasa de pobreza como medida de desarrollo regional. En este proceso, las variables de control son incorporadas de forma progresiva a los modelos econométricos.
En la Tabla 4, en las cinco regresiones, la variable dependiente es la tasa de pobreza. Encontramos que a medida que aumenta el ICR, disminuye la tasa de pobreza cantonal. El coeficiente obtenido entre las dos variables oscila entre -9.76 y -2.25; este coeficiente es estable y mantiene la significancia al 0.1% en todas las regresiones. Un resultado de interés, es que el número de empresas reduce de forma significativa la tasa de pobreza. Este resultado es consistente con los hallazgos de Alvarado, Peñarreta, Armas y Alvarado (2017) y Alvarado, Jiménez, Sánchez y Ponce (2019), quienes sugieren que la creación de empresas juega un rol clave en la reducción de la tasa de pobreza. Asimismo, al tratarse de datos de corte transversal, el ajuste del modelo es relativamente alto, ya que entre el 22-68% de las variaciones en el desarrollo regional están explicadas por el índice de competitividad regional y las variables de control.
Tabla 4 Resultados de la relación tasa de pobreza - ICR con dependencia espacial
| 1 | 2 | 3 | 4 | 5 | |
| ICR | -3.980* | -4.785 | -6.052* | -2.253 | -9.796 |
| (-2.48) | (1.63) | (-2.53) | (-1.15) | (1.09) | |
| Cercanía a mar | -1.206 | 1.651 | 4.657** | 4.322* | |
| (-0.40) | (0.84) | (2.70) | (2.52) | ||
| Polos de desarrollo | -60.44*** | 4.725 | -7.510 | -12.83 | |
| (-3.55) | (0.39) | (-0.76) | (-1.23) | ||
| Log (empleo) | 15.00*** | -23.77*** | -18.91*** | ||
| (9.77) | (-6.28) | (-4.03) | |||
| Log (Número de empresas) | -16.18*** | -11.48*** | -12.11*** | ||
| (-12.03) | (-7.82) | (-8.21) | |||
| Ruralidad | 9.828* | ||||
| (2.51) | |||||
| Educación primaria | 36.05*** | 35.65*** | |||
| (10.16) | (9.35) | ||||
| Educción secundaria | -4.433* | ||||
| (-2.61) | |||||
| Capacitación y formación | -0.475 | ||||
| (-1.86) | |||||
| Tasa de urbanización | -6.034 | ||||
| (-1.37) | |||||
| Ingenieros y profesionales | -0.0006 | ||||
| (-1.32) | |||||
| Constante | 2.04*** | 7.87*** | 2.31*** | 9.76** | 9.177 |
| (27.51) | (6.61) | (8.26) | (3.02) | (0.135) | |
| Rho | 0.398*** | 0.447* | 0.491*** | 0.520* | 0.657** |
| Lambda | 0.031*** | 0.037*** | 0.183*** | 0.610*** | 0.732*** |
| Observaciones | 224 | 224 | 221 | 221 | 221 |
| R2 Ajustado | 0.22 | 0.47 | 0.497 | 0.676 | 0.683 |
En general, los resultados obtenidos de la inclusión de la dependencia espacial son estadísticamente significativos en el modelo SARMA, tanto en rho como en lambda. Este resultado confirma la existencia de patrones espaciales en el proceso de desarrollo, en particular en la pobreza cantonal. En la práctica, la inclusión del espacio genera dos resultados. Primero, los estimadores sesgados de la Tabla 2 son corregidos con la inclusión de una variable relevante. Segundo, los valores que toma la pobreza en un cantón están condicionada por los valores que toma la pobreza en los cantones vecinos. Este resultado es coherente con las conclusiones de Jiménez & Alvarado (2018a). La particularidad de que el desarrollo de los territorios tiene dependencia espacial está justificado por los flujos entre unidades territoriales.
Conclusiones
Este trabajo construye un índice de competitividad cantonal para 221 cantones de Ecuador usando información censal, las Cuentas Nacionales del año 2010. Siguiendo la metodología del Foro Económico Mundial para medir la competitividad a nivel nacional, la metodología fue extrapolada a escala cantonal. Asimismo, se ha demostrado que el desarrollo cantonal está condicionado con la competitividad como un indicador más amplio e integral de desarrollo. Similar a otras investigaciones desarrolladas en países en desarrollo, el caso ecuatoriano muestra fuertes patrones de desigualdad del desarrollo económico y social que pudieron ser formalizados en el índice de competitividad regional.
La falta de datos temporales impide el análisis de la evolución de las disparidades del ICR. Sin embargo, a nivel cantonal no han existido cambios significativos en la estructura económica del país las últimas décadas como lo demuestran recientemente Torres-Gutiérrez, et al (2019). En consecuencia, el ICR se constituye en un indicador de desarrollo integral de los cantones. En general, el ICR demuestra que los cantones con mayor competitividad están más preparados para acelerar el desarrollo, mientras que en ellos, cantones con menor competitividad, requieren de políticas integrales, puesto que inversiones aisladas no tendrán la máxima efectividad.
En la segunda parte de la investigación demostramos que la competitividad cantonal tiene una fuerte capacidad explicativa del desarrollo de los territorios, en particular de la tasa de pobreza cantonal, donde existen patrones de dependencia espacial. A partir del diagnóstico de dependencia espacial, estimamos un modelo SARMA, mediante el cual demostramos que el desarrollo cantonal esta fuertemente asociado con el índice de competitividad regional y que el número de empresas juega un rol relevante en la determinación de la tasa de pobreza. Las posibles implicaciones de política derivados de esta investigación es que el estado debería fomentar el surgimiento de empresas estables en el tiempo, mejorar la inversión en infraestructura, educación y salud, e incluir la interacción de los territorios en el diseño y ejecución de políticas públicas. Futuras investigaciones pueden ofrecer una mayor profundización en los pesos de las variables y las dimensiones, puesto que existen variables que pueden ser más relevante que otras para alcanzar el desarrollo de los cantones.