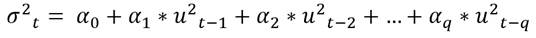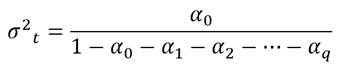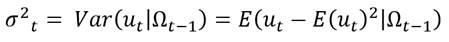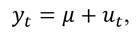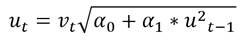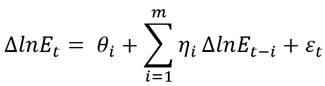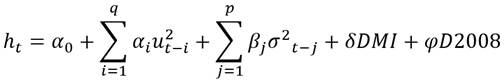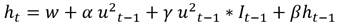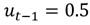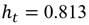Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introducción
Desde inicios de la década de 1990, las economías avanzadas y en desarrollo, comenzaron a adoptar el régimen de Metas de Inflación (MI) como el marco de política monetaria. El principio básico es ajustar la política de tasa de interés para mantener el pronóstico inflacionario lo más cercano posible a la meta de inflación y lograr así, la estabilidad de precios como el objetivo primario. El régimen envuelve algunos aspectos institucionales tales como: la independencia del banco central, la transparencia y la rendición de cuentas para mejorar la efectividad y credibilidad de la política monetaria.
Para el año 2018, existían 41 países desarrollados y en desarrollo, que oficialmente utilizaban este régimen. Para Rose (2007) el paradigma de MI con un tipo de cambio flotante provee un sistema monetario internacional estable.
Aunque el régimen de MI ha ganado amplia aceptación, la crisis financiera global (CFG) que comenzó en Estados Unidos en agosto de 2007, desencadenó un considerable debate respecto a la conducción de la política monetaria bajo este paradigma. En las dos décadas que antecedieron la crisis, se desarrolló un periodo de disminución en la inflación y el crecimiento económico en la economía mundial, denominado “la gran moderación” o “los años dorados de los bancos centrales” (Bernanke, 2004). Durante este periodo el esquema de MI fue ampliamente adoptado; sin embargo, una de las críticas es que este régimen fue introducido bajo condiciones macroeconómicas relativamente benignas, generando choques sobre la economía, relativamente moderados (Stock y Watson, 2003). Esto evitó que el régimen fuera probado con impactos mayores y en realidad, el adecuado desarrollo de los países se debió a la buena suerte traída por el periodo de la gran moderación, más no por una política sustentada en el paradigma de las MI (Ball y Sheridan, 2005).
Hasta principios del 2008, existía poco escepticismo sobre la eficacia de las MI y pocos pensaban que existieran razones para abandonar dicho marco de política monetaria. No obstante, la CFG marcó el final de la gran moderación y el régimen de MI propuesto por el Nuevo Consenso Macroeconómico comenzó a evidenciar falencias (Arestis y Sawyer, 2013). La principal crítica es que al requerir que los bancos centrales se enfocaran en la estabilidad de precios, se ignoró la estabilidad financiera y el crecimiento económico.
Los datos sobre los agregados económicos en la región latinoamericana y a escala nacional son difíciles de obtener; y más aún, si se trata de datos de alta frecuencia. Por esta razón, se ha privilegiado obtener la mayor cantidad de datos disponibles de la variable de estudio, para poder identificar el valor esperado, exclusivamente mediante su pasado; y a partir de esta estructura, determinar la varianza condicional, mediante su estructura autorregresiva, y el efecto que han tenido sobre ella dos de los principales eventos económicos de los últimos veinticinco años. Por un lado, la implementación del régimen de metas de inflación y por el otro, la crisis financiera global de 2008.
Los resultados indican que las depreciaciones cambiarias generan mayor volatilidad en el tipo de cambio, si se les compara con los impactos generados por apreciaciones de igual magnitud. También, se señala que el paradigma de MI, que requiere de un tipo de cambio flexible, ha desencadenado una mayor volatilidad en las divisas de la región, especialmente en Brasil, Chile y México. Respecto a los efectos de la CFG de 2008, se comprueba que en los años posteriores se ha presentado un incremento en la volatilidad cambiaria de la región, siendo México y Brasil las economías más afectadas.
En la siguiente sección se discute la literatura referente al efecto paralelo que ha generado la implementación del régimen de MI y la CFG de 2008 sobre la varianza condicional del tipo de cambio. La tercera sección presenta la metodología econométrica utilizada para estimar, de manera precisa, la volatilidad del tipo de cambio y su efecto asimétrico. La calibración se obtiene a través de su estructura autorregresiva, del impacto causado por la implementación del esquema de MI y del efecto provocado por la gran crisis financiera en los Estados Unidos de América. En la cuarta sección se muestran los resultados empíricos y en la quinta sección se concluye.
2. Revisión de la literatura
Las fuertes crisis que golpearon a las economías emergentes entre mediados de 1990 y principios de 2000, llevaron a la desvinculación de muchos regímenes cambiarios fijos y a la transición hacía una mayor flexibilidad cambiaria. Con esta adopción muchos países también se movieron hacia una conducción de su política monetaria anclada en el régimen de metas de inflación (Ouyang, et al., 2016).
2.1 El régimen de metas de inflación
De acuerdo con el Annual Report on Exchange Arrangements and Exchange Restriction, del Fondo Monetario Internacional, 41 países habían adoptado el régimen de MI para el año 20181. La adopción de este régimen implica el anuncio público de metas numéricas para la inflación, con un compromiso institucional por parte de la autoridad monetaria para lograr estas metas, generalmente en un horizonte de mediano plazo. De acuerdo con Perrotini (2007), el régimen de MI incluye los siguientes cinco aspectos: primero, provee un marco preciso de política monetaria, el banco central anuncia objetivos oficiales de la tasa de inflación; segundo, la política monetaria está sujeta a reglas , estrictas o flexibles; tercero, la tasa de interés es el único instrumento de la política, estabiliza la inflación y equilibra la oferta y demanda agregadas (ancla nominal de la economía); cuarto, el régimen es operado por un banco central independiente cuya única preocupación es la tasa de interés; y quinto, se considera que el impacto de la política monetaria en objetivos distintos a la estabilidad de precios no es relevante. Berganza y Broto (2012), establecen que los primeros países de la región latinoaméricana que implementaron este esquema son Brasil (1999), Chile (1999), Colombia (1999), México (2001) y el Perú (2002).
En América Latina la mayoría de los países manejan un esquema en su tipo de cambio denominado acuerdo de flotación (Brasil, Colombia y Perú); mientras que, el resto de los países de la muestra mantienen un acuerdo de libre flotación (Chile y México). En el primero, el tipo de cambio se determina en gran medida por el mercado, sin una trayectoria comprobable o predecible para el tipo de cambio. La intervención en el mercado cambiario puede ser directa o indirecta, y dicha intervención sirve para moderar el tipo de cambio y evitar fluctuaciones indebidas. En el segundo, el tipo de cambio se clasifica como de libre flotación si las intervenciones cambiarias2 ocurren excepcionalmente y tiene como objetivo abordar las condiciones desordenadas del mercado, y si las autoridades han proporcionado información o datos que confirman que la intervención se ha limitado a un máximo de tres casos en los seis meses anteriores, cada uno de los cuales dura no más de tres días hábiles (FMI, 2018).
Un tipo de cambio nominal flexible se constituye, al menos desde un punto de vista teórico, como un requerimiento para el buen funcionamiento de un régimen de MI. Su racionalidad se basa en el dilema de política económica denominado la “triada incompatible”; ya que, en un contexto de libre movilidad de capitales y una política monetaria independiente no puede ser combinada con un tipo de cambio fijo (Obstfeld et al., 2005). Sin embargo, se ha establecido que uno de los costos del régimen de MI es precisamente una mayor volatilidad de los tipos de cambio como resultado de la adopción de un régimen de tipo de cambio flotante (Cavoli, 2009).
2.2 La gran recesión de 2008
La teoría neoliberal alentó la liberalización en el comercio y en los flujos de capital. Sin embargo, la liberalización de los flujos de crédito, a menudo, no fue acompañada de una supervisión prudencial3, ni de una adecuada regulación, conduciendo a crisis financieras desde mediados de 1990 hasta la crisis de 2008 (Hsu, 2013). De esta manera, el quiebre de las políticas de consenso de Washington, dejó al descubierto la laguna existente en la teoría del paradigma neoliberal.
Durante el inicio de la CFG de 2008, los mercados bursátiles mundiales cayeron y los bancos globales experimentaron fallas a gran escala. Como es ampliamente conocido, la crisis comenzó en los Estados Unidos con la sobrevaloración de los activos hipotecarios de alto riesgo. Se otorgaron hipotecas muy volátiles a personas que carecían de ingresos suficientes. A medida que estas personas no contaban con la solvencia para enfrentar sus obligaciones, comenzaban a perder sus hogares; dando pie al surgimiento de nuevos activos sintéticos con garantía hipotecaria basados en estos préstamos de alto riesgo.
Estos activos se encontraban ampliamente distribuidos en todo el sistema financiero americano. A medida que los precios de las casas en los Estados Unidos comenzaron a caer, los activos hipotecarios se derrumbaron y amenazaron con derribar a las instituciones financieras más poderosas del orbe. El estrés generado dio lugar a una mayor volatilidad en el tipo de cambio de los mercados emergentes (Coudert et al., 2011).
En América Latina se implementaron diversas estrategias para absorber parte de los choques iniciales a través de la flexibilidad de sus tipos de cambio; todos ellos experimentaron, a su vez, una apreciación de sus monedas desde el segundo trimestre del 2009, cuando los mercados de capitales internacionales comenzaron a normalizarse (Cohen, 2012). Sin embargo, esta flexibilidad cambiaria, que es una característica inherente del régimen de MI; no resultó ser una panacea, ya que generó una significativa inestabilidad en el tipo de cambio nominal (Frenkel y Rapetti, 2010).
Se ha prestado mucha atención al impacto que ha generado el régimen de MI en varios indicadores del desarrollo económico. Sin embargo, existen pocos estudios que hayan investigado el efecto conjunto del esquema de MI y el impacto derivado de la crisis financiera global del 2008 sobre la volatilidad del tipo de cambio. En particular Rose (2014) centra su investigación en la CFG y su periodo posterior (2007-2012). Por su parte Edwards (2006) encuentra que el fenómeno del incremento de volatilidad con un régimen de MI se debe principalmente a la adopción de un tipo de cambio flotante. Es decir, la adopción del régimen de MI, per se no incrementa el grado de volatilidad en el tipo de cambio, sino que es el régimen cambiario que se adopta el que estimula la volatilidad. Rose (2007), encuentra que el régimen de MI tiende a disminuir la volatilidad del tipo de cambio respecto de aquellos países que no implementan las metas de inflación. Berganza y Broto (2012), establecen que aun cuando la adopción del régimen de MI podría llevar a una mayor inestabilidad del tipo de cambio, las intervenciones esterilizadas en el mercado cambiario en países con MI parecen ser más efectivas en la contención de la volatilidad del tipo de cambio si se les compara con aquellos países que no implementaron el régimen de MI.
3. Materiales y métodos
La volatilidad es la medida de riesgo más común en finanzas y se refiere al riesgo asociado con los movimientos alternados a la alza, así como a la baja del valor de una tasa de cambio. Se ha demostrado que la varianza no condicional es menos eficiente que la varianza condicional, ya que esta última considera la acumulación de volatilidad. El término condicional se refiere al hecho de que el modelo se encuentra sujeto al conocimiento de la volatilidad del periodo previo (Brooks, 2015).
Resulta ilustrativo realizar una explicación sobre los hechos estilizados más relevantes que experimentan las series de tiempo del tipo de cambio. Es bien sabido que la mayoría de las series financieras, presentan algunos patrones sintomáticos, que son esenciales para una correcta especificación, estimación y pronóstico de los modelos apropiados.
Varios investigadores han identificado estas regularidades empíricas, al grado de convertirse en hechos estilizados. Se puede listar entre los más comunes: 1) colas pesadas; 2) acumulación de volatilidad; 3) efecto apalancamiento (asimetría en los impactos); y 4) co-movimientos en la volatilidad (Mandelbrot ,1963).
Basado en el conocimiento sobre la existencia de la acumulación de volatilidad, Engle (1982) propone su modelo de Heteroscedasticidad Condicional Autorregresiva (ARCH). Este fue el primero de los modelos que permitió el pronóstico de la volatilidad condicional. La idea fundamental es que no asume una varianza constante (Engle 1982, Brooks, 2015). El modelo ARCH es estimado tomando los errores cuadráticos y permitiendo que el error dependa de los “q” rezagos. El modelo ARCH(q) se encuentra determinado como:
(1)En este esquema la varianza no condicional se representa por:
Mientras que la varianza condicional se determina por:
Donde Ω representa el conjunto de información. De esta manera si considere el modelo AR(1):
(2)Donde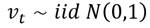 
, 
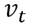es independiente de 
, 
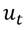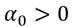y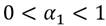 
. La curtosis de la distribución no condicional es igual a 
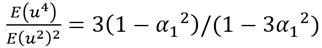. Y si esta es igual a 3 se considera una distribución normal; mientras que, si α 1 se aproxima a 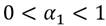, entonces la curtosis excederá a 3 y la distribución será leptocurtica.
Bollerslev (1986) y Taylor (1986) se encargaron de extender el modelo ARCH para permitir una estructura de rezagos que incorpora el término de varianza condicional cuadrática como una variable explicativa. Esto permite que la varianza condicional siga un proceso ARMA. Cabe señalar que los modelos GARCH son usualmente más parsimoniosos4. El modelo GARCH (q,p) se representa como:
(3)La principal restricción de este modelo es que todas las variables explicativas en un modelo GARCH (q,p), y por lo tanto de un modelo ARCH(q), deben ser positivas 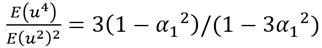, (restricción de no negatividad), además se debe cumplir la condición 
.
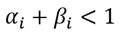3.1 Efecto asimétrico y prueba de sesgo en signo y magnitud
Una de las mayores limitaciones del modelo GARCH (q,p) es la suposición de que los impactos, tanto de los choques positivos como de los negativos, de la media condicional sobre la varianza condicional son de igual magnitud. Black (1976) fue el primero en notar que los cambios en los rendimientos de las acciones a menudo muestran una tendencia a estar negativamente correlacionados con los cambios en la volatilidad de los rendimientos, es decir, la volatilidad tiende a aumentar en respuesta a las malas noticias y a caer como resultado de las buenas noticias. Este fenómeno es denominado efecto apalancamiento.
Para identificar la presencia de un efecto asimétrico Engle y Ng (1993) propusieron una prueba diagnóstico, se trata de una estructura que permite descubrir la relación empírica entre los choques (noticias buenas y malas) y la volatilidad. La denominada prueba de sesgo, en signo y magnitud, sirve para determinar si se requiere de un modelo asimétrico para modelar la volatilidad o si el modelo simétrico GARCH es el adecuado. En la práctica, la prueba de Engle-Ng, usualmente es aplicada a los residuos cuadráticos estandarizados de un modelo GARCH de la tasa de crecimiento porcentual de la variable estimada. La prueba se explica de la siguiente manera:
(4)Donde ε 2 t residuos estandarizados elevados al cuadrado, ϕ 0 es el coeficiente de intersección, υ t es un término de error independiente e idénticamente distribuido, 𝜙 1 representa el posible sesgo respecto al signo, S - t-1 que se construye como una variable dummy que toma el valor de 1 cuando 𝑢 𝑡−1 es negativo y cero en otro caso y que además sirve para capturar tres efectos diferentes.
El sesgo en signo: Si 
El sesgo en magnitude debido a choques negativos: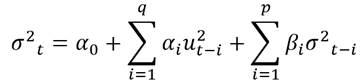
El sesgo en magnitude debido a choques positivos: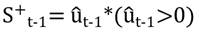 
Incorporando los tres diferentes efectos Engle y Ng (1993) derivaron una única ecuación que se representa como:
(5)En esta ecuación, la significancia estadística de ϕ 1 indica la presencia de un sesgo en el signo, donde choques positivos y negativos presentan un impacto diferenciado sobre la volatilidad futura. Y por otro lado, la significancia de 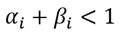y 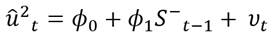sugieren la presencia de un sesgo de magnitud, donde no solamente el signo, sino la magnitud del choque, son importantes. Para su comprobación se realiza una prueba de hipótesis conjunta calculada como 
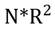(N es el tamaño de la muesta y 
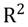el coeficiente de determinación), que sigue una distribución asintótica 
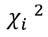con tres grados de libertad bajo la hipótesis nula de que no existen efectos asimétricos.
Existen formulaciones asimétricas que han ganado popularidad debido a su efectividad para capturar el efecto asimétrico de la volatilidad. Una de las más conocidas es el modelo GJR-GARCH, nombrados así en honor de Glosten, Jagannathan y Runkle (1993). Se trata de una extensión de los modelos GARCH, con la adición de un término que captura la posible asimetría. El modelo GJR-GARCH(q,p) tiene la siguiente representación:
(6)
En el modelo, el efecto de las buenas noticias muestra su impacto en el coeficiente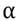 
, mientras que las malas noticias muestran su impacto a través de 
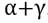. Además, si 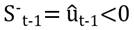el impacto de las noticias es asimétrico, y si 
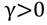es estadísticamente significativo esto sugiere que existe un efecto apalancamiento. El modelo incluso es aceptable cuando 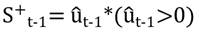, siempre y cuando 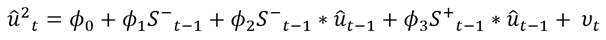(Brooks, 2015).
3.2 Las metas de inflación, la crisis financiera global y su efecto en la volatilidad cambiaria
En el presente estudio, se busca analizar el impacto de las innovaciones asimétricas sobre la volatilidad condicional del tipo de cambio. Los choques en la forma de noticias negativas traería como consecuencia un mayor impacto sobre la varianza condicional de del tipo de cambio si se le compara con sus contrapartes positivas. Adicionalmente, se busca identificar el efecto que ha generado la adopción del régimen de MI, así como las variaciones generadas en la volatilidad cambiaria como resultado de la CFG de 2008.
Con base en los trabajos de Edwards (2006), Rose (2007) y Berganza y Broto (2012), se especifica un modelo de volatilidad condicional asimétrico del tipo de cambio para cada una de las economías estudiadas. La estructura del modelo econométrico se describe como:
(7)
(8)Donde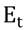 
es el tipo de cambio; 
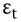es el termino de perturbación estocástica. Siguiendo el desarrollo de Edwards (2006), se incorpora la variable dummy DMI en la ecuación de la varianza condicional para capturar el efecto que ha tenido el régimen de MI, en el incremento o atenuación de la variabilidad del tipo de cambio. Adicionalmente, se agrega otra variable dummy D2008, que estima el efecto provocado por la crisis de 2008. El impacto de estas variables puede ser evaluado a través del signo de sus coeficientes. Un coeficiente positivo significa que el incremento de la volatilidad del tipo de cambio se encuentra asociado con la adopción del régimen de MI; mientras que, un coeficiente negativo implicaría que la política de MI ayuda a reducir la volatilidad del tipo de cambio (Mishkin y Sabastano 2001; Gali y Monacelli, 2005). De igual forma se interpretan los signos en la variable que captura el efecto de la CFG de 2008.
4. Resultados y Discusión
Se consideró una muestra de 5 países emergentes de la región latinoamericana. Estos países son Brasil, Chile, Colombia, México y Perú. La muestra de datos corresponde a las observaciones diarias del tipo de cambio de estas naciones (real brasileño, peso chileno, peso colombiano, peso mexicano y sol peruano), los datos fueron obtenidos del banco central de cada país. El periodo de muestra para el estudio abarca enero de 1995 a mayo de 2019, para Brasil, Chile, Colombia y México (más de seis mil observaciones); mientras que, para el caso de Perú el periodo corresponde a enero de 1997 a mayo de 2019 (5574 observaciones). La selección del periodo obedeció a la disponibilidad de los datos. El tipo de cambio utilizado es la moneda local por unidad de dólar estadounidense.
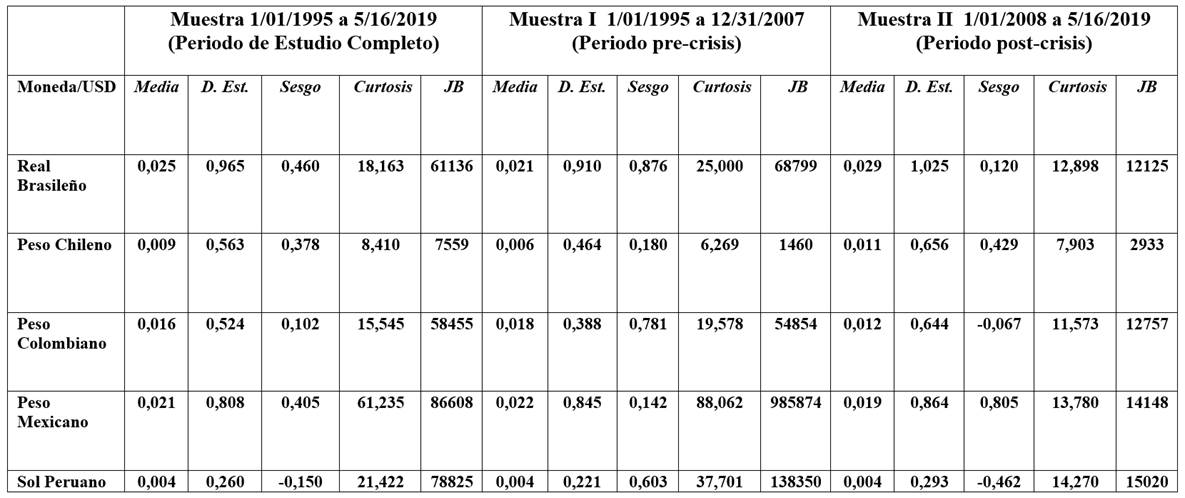
El estudio comienza con un análisis sobre las estadística descriptivas de las series de tiempo para la tasa de cambio porcentual del tipo de cambio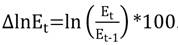 
. Las variables de los cinco países exhiben el fenómeno de colas pesadas, es decir, cuando la distribución de la tasa de cambio porcentual del tipo de cambio es comparada con la distribución normal, se observa el fenómeno, en términos de un exceso de curtosis (leptocurtosis). La tasa de cambio porcentual de la moneda mexicana es la más apuntalada.
En cuanto al segundo hecho estilizado, es evidente que las variables presentan una marcada acumulación de volatilidad en diferentes fechas; sin embargo, todas ellas coinciden en que el mayor incremento de su volatilidad se presentó en el año 2008. Este fenómeno muestra que cuando la volatilidad es alta, es probable que permanezca alta; y viceversa (Figura 1); además, parece que posterior a la CFG de 2008, la volatilidad se ha incrementado respecto a su periodo previo. Otra regularidad empírica que no es perceptible a simple vista es que, las buenas y malas noticias presentan impactos diferenciados sobre la volatilidad del tipo de cambio, es decir, existe un efecto asimétrico. Finalmente, se puede observar que la tasa de cambio porcentual de las cinco monedas parece acompañarse, es decir, presentan un co-movimiento, esto quiere decir que los mercados cambiarios exhiben fluctuaciones paralelas que parecen acompañarse.
En la tabla 1, se puede ver claramente como antes de la CFG de 2008, los movimientos en la variable son muy similares; y, después de la crisis, sus trayectorias son aún más parecidas. Destacan dos comportamientos, la desviación estándar se incrementó en el periodo post-crisis en todas las economías; mientras que, la curtosis se redujo considerablemente, en la mayoría de los países analizados.
Las estadísticas también muestran que la prueba de normalidad Jarque-Bera comprueba que no existe normalidad en su distribución. Por tanto, se deberá identificar una función de distribución condicional adecuada, que puede ser la distribución t-student, o la distribución de errores generalizados, cada una con sus respectivas variaciones (grados de libertad y parámetros fijos).
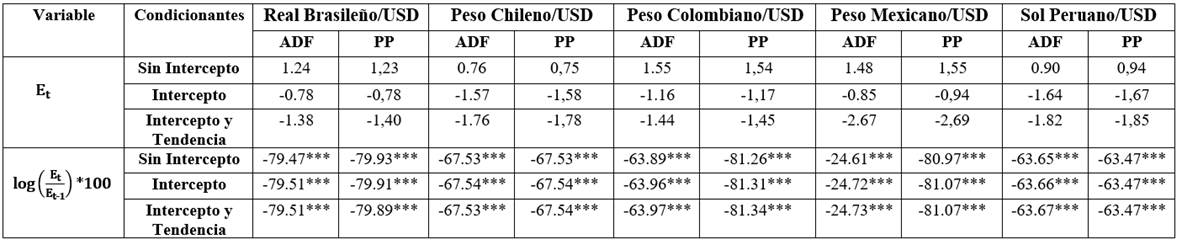
Nota: Los niveles de significancia son: * 10%, ** 5%, *** 1%. Los estadísticos tau de la prueba ADF y PP son: -3.12, -3.41 y -3.95 para su respectivo nivel de significancia. ADF significa prueba Dickey-Fuller Aumentada y PP significa Prueba Phillips Perron, π representa el tipo de cambio.
Las condiciones de estacionariedad de los tipos de cambio son verificadas mediante pruebas de hipótesis (tabla 2); para ello, se utilizaron dos especificaciones: 1) la prueba de raíz unitaria Dickey-Fuller Aumentada (ADF) y la prueba Phillips-Perron (PP). Ambas pruebas se realizaron a nivel y en primeras diferencias. Los resultados confirman la existencia de una raíz unitaria con la variable a nivel, para todas las divisas. Y por el contrario, cuando la prueba de raíz unitaria es aplicada sobre la tasa de cambio porcentual del tipo de cambio, se observa que todas las monedas presentan estacionariedad a un nivel de significancia del 1%. Adicionalmente, se aplicaron pruebas de raíz unitaria con cambio estructural y se identificó que la mayoría de los países presentaron su principal quiebre en el año 2008.
Los tipos de cambio de las economías latinoamericanas han experimentado varios choques a lo largo del periodo de estudio. Las gráficas de la figura 1 muestran que todas las divisas se han depreciado respecto al tipo de cambio de los Estados Unidos de América, si se compara el precio inicial contra el precio final. Otro efecto perceptible es la acumulación de volatilidad; en las gráficas de cada país se vislumbra que, a partir de mediados de la década de los noventa y hasta el 2008, un periodo inmerso en la época de la gran moderación5, la volatilidad de las diferentes divisas experimentó un periodo de estabilidad, mientras que, en los años posteriores a la CFG de 2008, se observa una mayor presencia de inestabilidad.
Las gráficas también muestran un claro efecto de acompañamiento (co-movimientos), esto es muestra de que los tipos de cambio han evolucionado con una tendencia muy similar, especialmente después de la crisis. Finalmente, las series de tiempo también presentan un evidente efecto asimétrico; lo anterior se fundamenta en que cuando se ha presentado una mayor depreciación de la moneda, también se identifica una mayor acumulación de volatilidad. Esto muestra que los impactos positivos y negativos, entendidos como apreciaciones y depreciaciones de la moneda, presentan un efecto diferenciado en la volatilidad del tipo de cambio.
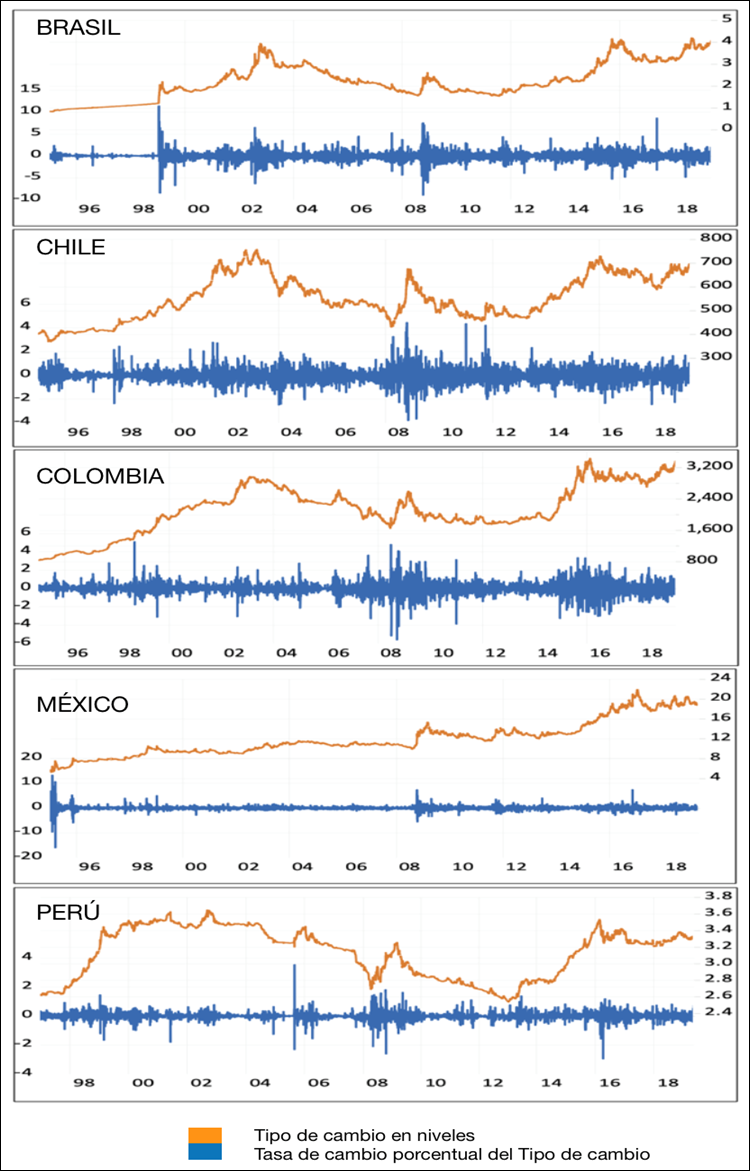
Fuente: Elaboración Propia
Figura 1 Gráficas de los tipos de cambio en niveles y en tasas de crecimiento
4.1 Modelos GARCH para la volatilidad cambiaria
Una vez identificados los principales hechos estilizados, se comprobó formalmente la existencia de un efecto GARCH, mediante la prueba de McLeod y Li (1983). Para ello se utilizó una muestra de residuos de tamaño N, bajo la hipótesis nula de que no existen errores GARCH; mientras que, el estadístico de prueba N*R2 converge a una distribución χ2. Si N*R2 es suficientemente grande utilizando los niveles de significancia correspondientes, rechazar la hipótesis nula sería muestra de la existencia de un efecto GARCH. Por otra parte, si N*R2 es suficientemente bajo, es posible concluir que no existe un efecto GARCH. En la tabla 3, se proporciona la evidencia.
Tabla 3 Prueba para determinar la existencia de efectos GARCH
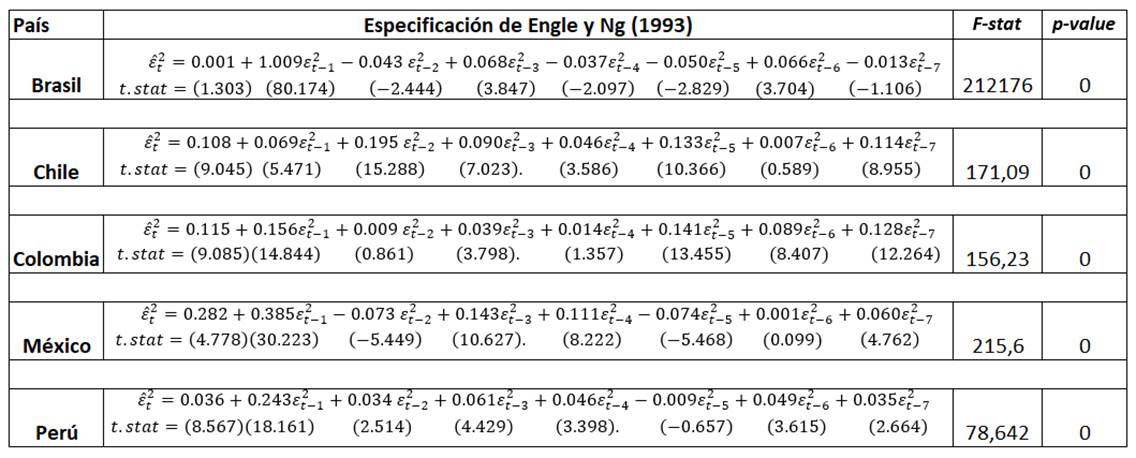
Fuente: Elaboración propia.
Nota: Los valores en paréntesis representan los valores estadísticos de la t de student
Estos resultados comprueban que en la mayoría de los rezagos se identifica una clara existencia de volatilidad condicional. Con base en ello, se busca estimar un modelo óptimo, tanto en media como en varianza, y que además, incluya el efecto individual que ha tenido; por un lado, la implementación del régimen de MI y por el otro, las repercusiones de la CFG de 2008 en la región latinoamericana. En la tabla 4, se muestra la estimación de los modelos desarrollados mediante el método de Cuasi Máxima Verosimilitud.
Tabla 4 Resultados de las regresiones ARMA-GARCH simétricos
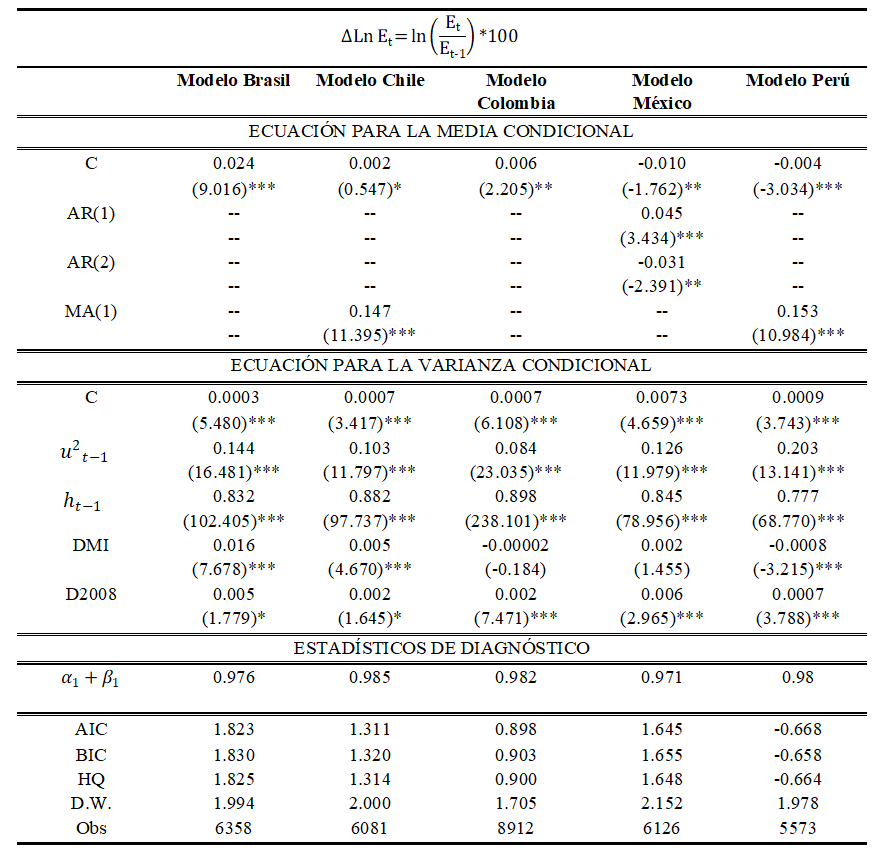
Fuente: Elaboración propia.
Nota: Los niveles de significancia son: * 10%, ** 5%, *** 1%
Los resultados muestran que la media condicional de Brasil y Colombia se comporta como un proceso ruido blanco; mientras que para Chile, México y Perú se encontró una estructura con componentes autorregresivos y de medias móviles, resultando todos ellos estadísticamente significativos, además de cumplirse las condiciones de estabilidad.
En la ecuación de la varianza condicional se pudo identificar claramente que los coeficientes cumplen con las condiciones de no negatividad en 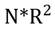y 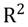(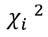, respectivamente) y con la condición de estabilidad 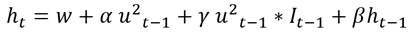. También se aprecia como la implementación del régimen de MI, capturado mediante la variable dummy (DMI), ha significado un aumento de la volatilidad para Brasil y Chile; mientras que, para Perú ha disminuido. En lo que respecta al impacto sufrido tras la CFG de 2008, los resultados son claros, pues se observa un incremento de la volatilidad en todas las economías, siendo México y Brasil los países en donde más se ha incrementado.
Una de las principales restricciones que imponen los modelos GARCH es que suponen una respuesta simétrica de la volatilidad ante choques positivos y negativos. Esto surge como consecuencia de que, la varianza condicional es una función de las magnitudes de los residuos rezagados y no de su signo, pues al elevar al cuadrado estos errores, el signo se pierde. Ante esta pesada restricción, se han propuesto modelos que permiten capturar el efecto asimétrico presente en las variables que exhiben un marcado apuntalamiento (leptocurtosis) en su distribución. Por tal motivo, se estima la prueba de sesgo en signo y magnitud desarrollada por Engle y Ng (1993), cuyos resultados se presentan en la tabla 5.
Tabla 5 Prueba de sesgo en signo y magnitud
Fuente: Elaboración propia.
Nota: Los valores en paréntesis representan los valores estadísticos de la t de student.
Los resultados muestran que el coeficiente de intersección, que representa los choques positivos, es estadísticamente significativo en la mayoría de las economías estudiadas, esto indica que los impactos de signo positivo tienen una mayor influencia que aquellos con signo negativo; respecto a la magnitud, Chile, Colombia, y México exhiben un mayor impacto por parte de los coeficiente positivos respecto a los negativos, siendo todos ellos estadísticamente significativos. Lo anterior presenta una clara tendencia a que los impactos positivos (depreciaciones) estimulan la presencia de volatilidad. Partiendo de estos hallazgos, se estima un modelo GJR-GARCH, que permite capturar la asimetría en los impactos.
4.2 El efecto asimétrico en el cambio porcentual de las divisas
Si los eventos positivos o negativos presentan un mayor efecto sobre la volatilidad estos serán medidos por el coeficiente γ de la ecuación (6). Los resultados del modelo hibrido, que incluyen la media y la varianza condicional, y que consideran innovaciones t-student, se muestran en la tabla 6.
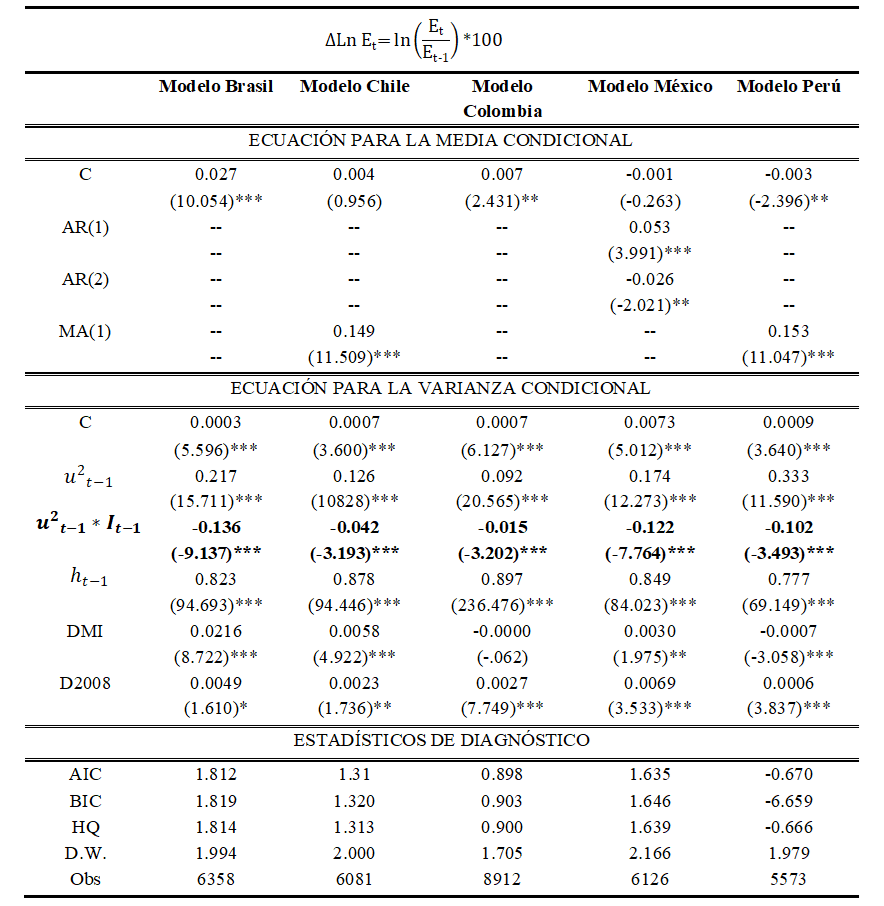
Tabla 6 Resultados de las regresiones ARMA-GJR-GARCH
Fuente: Elaboración propia.
Nota: Los niveles de significancia son: * 10%, ** 5%, *** 1%
Se puede inferir en la ecuación de la media condicional que tanto los coeficientes de intersección, como los coeficientes de los procesos autorregresivos y de medias móviles presentan una elevada significancia estadística. Sin embargo, la ecuación más importante en esta investigación es la varianza condicional, pues en ella podemos identificar los determinantes que supeditan la evolución de la volatilidad cambiaria. Se identifica una vez más que los coeficientes cumplen con las condiciones de no negatividad y que, si bien es cierto, el coeficiente γ es negativo en todas las ecuaciones; también es cierto que, se cumple la condición 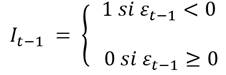, es decir que el modelo es aceptable. Lo anterior pone de manifiesto que son los choques positivos, es decir las depreciaciones, las que causan un mayor incremento en la volatilidad cambiaria. El impacto es más severo en Perú y Brasil6 con un 0.333 y un 0.217 respectivamente, le siguen México, Chile y Colombia con 0.174, 0.126 y 0.092. Si hablamos del impacto que generan los choques negativos (α+γ), es decir, las apreciaciones cambiarias, podemos identificar que los impactos para Brasil, Chile, Colombia, México y Perú son 0.081, 0.084, 0.077, 0.052 y 0.231 respectivamente, lo que comprueba que para todos los países, una política de apreciación de la moneda genera una menor inestabilidad en las divisas, si se le compara con el efecto que impone una política cambiaria que busque la depreciación.
Respecto al impacto que ha generado la implementación del régimen de MI sobre la volatilidad en las divisas, se advierte que esta ha provocado una mayor inestabilidad en Brasil, Chile y México; mientras que en Colombia el coeficiente es cero y no significativo, y en Perú el coeficiente es negativo y significativo. Adicionalmente, se infiere que Brasil es la economía en la que más se ha incrementado la volatilidad del tipo de cambio como consecuencia de la implementación del esquema neoliberal de MI.
Estos resultados son consistentes con los obtenidos por Berganza y Broto (2012) y Ouyang (2016). Por su parte, el coeficiente que captura el efecto que ha generado la CFG de 2008 en la varianza condicional, muestra que para las cinco economías los resultados son positivos y estadísticamente significativos y que las economías que más han sufrido los efectos de esta crisis son México y Brasil (0.006 y 0.004), seguidos por Chile y Colombia con 0.002; mientras que, Perú solo exhibe un efecto mínimo de 0.0006.
Todas las ecuaciones fueron seleccionadas en función de los criterios de información de Akaike (AIC), de Schwarz (BIC) y de Hannan y Quinn (HQ).
5. Conclusiones
En años recientes ha comenzado a crecer el interés académico de explorar el impacto macroeconómico del régimen de MI y de las crisis financieras que lo han acompañado. La CFG de 2008 comenzó a generar profundas dudas sobre la conducción de la política monetaria y cambiaria. De esta manera, el paradigma de MI, implementado por la corriente de pensamiento neoliberal se ha enfrentado a impactos económicos que han hecho tambalear sus cimientos.
Podría decirse que la principal crítica se refiere a la aparente incapacidad del esquema de MI para responder adecuadamente a los choques de oferta agregada, la inflación de los precios de los activos y las preocupaciones de estabilidad financiera (Walsh, 2009). Esta investigación busca contribuir a la literatura de una manera más específica, se examina el impacto generado por la implementación del régimen de MI y los efectos económicos negativos que le acompañan (CFG de 2008), en la volatilidad del tipo de cambio. El estudio considera una de las regiones del planeta que se ha visto más golpeada por las crisis financieras. Para ello, se buscó ser exhaustivo en el tratamiento de los datos, además de que se utilizó la mayor cantidad de observaciones disponibles (diarios); lo anterior, indudablemente posibilita una mejor interpretación del fenómeno de la volatilidad, que se encuentra implícita en los tipos de cambio, ya que permite identificar aspectos que no serían visibles en datos trimestrales o mensuales.
El documento presenta una serie de hipótesis sobre el impacto esperado del régimen de MI y del efecto generado por la CFG de 2008 en la volatilidad del tipo de cambio (utilizado la moneda local por unidad de dólar estadounidense). Sobre la base de una muestra de las principales divisas latinoamericanas (real brasileño, peso chileno, peso colombiano, peso mexicano y sol peruano), durante el periodo 1995 a 2019, se encuentran los siguientes resultados: 1) Se comprueba, para todas las economías analizadas, que existe un mayor impacto, estadísticamente significativo, de los choques positivos (depreciaciones cambiarias) sobre la varianza condicional, si se comparan con los impactos negativos (apreciaciones cambiarias) de igual magnitud; 2) La implementación del régimen de MI parece haber incrementado la volatilidad de los tipos de cambio en Brasil, Chile y México; mientras que, en Perú parece haberla atenuado; 3) Los datos estadísticos soportan la hipótesis de que la CFG del 2008 ha estimulado la generación de un periodo de mayor volatilidad en todas las economías de la región, siendo México y Brasil las economías que han experimentado un mayor aumento de inestabilidad en sus divisas.
