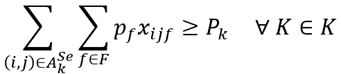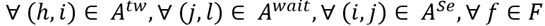1. INTRODUCTION
The vehicle scheduling problem (VSP) has become an extensively studied research area in the last decades; in this context, an ultimate overview of literature in planning and control of bus transport exists in (Ibarra-Rojas et al., 2015). However, the principal problem consists in the process of minimizing the assignment costs of vehicles to a given set of timetabled trips, including two main constraints as follows: (i) each trip is assigned exactly once; and (ii) each vehicle performs a feasible sequence of trips. Each selected vehicle starts and ends a trip in the depot with the travel time and stations fixed and previously defined. Different approaches to model the VSP have been developed, as well as solution methods and extensions for a better reality representation, e.g., the inclusion of multiple- depots and heterogeneous fleet (Bunte and Kliewer, 2009). The latter, however, has received little attention in the public transportation literature. The literature of vehicle scheduling covers usually one type of vehicle; however, in practice, more than one type is used (Ceder, 2011). In the context of heterogeneous fleet, the vehicle scheduling problem is known as the vehicle-type scheduling problem (VTSP). Compared to the VSP, VTSP increases the degrees of freedom for planning decisions, and therefore, the problem complexity.
By including time windows in the VTSP we allow to shift scheduled trips within defined interval, i.e., we introduce flexibility in the departure times of trips, increasing operational advantages on the number of required vehicles. When considering heterogeneous fleet, time windows become even more useful since the timetabling can be slightly redefined according to the demand and the bus type assigned to cover it.
Although some research considers timetable flexibility (Desfontaines and Desaulniers, 2017), the studies neglected the heterogeneous fleet issue. Desaulniers et al., (1998) and Hadjar and Soumis, (2009) studied the problem using column generation. A multi-commodity network flow model based on a time-space network, where each trip might be represented by multiple arcs if alternative start times create new possible connections between trips was introduced by (Kramkowski, 2009). Heuristic were developed to eliminate irrelevant alternative trips towards reducing the model size and speed up the solution by a commercial MIP solver. V. Schmid and J. F. Ehmke (Schmid, and Ehmke, 2015) developed a two-phase heuristic to integrate the timetabling and the VSP. First, the heuristic finds good vehicle schedules and then determines the best feasible timetable (with respect to headways only) considering these schedules. Ceder (2011) proposed a heuristic way to simultaneously construct vehicle schedules and a timetable with even headways or even load per vehicle. Subsequently, (Laporte, 2017) and (Lui and Ceder, 2017) took into account passenger assignment to the problem, considering transfer in some stations. However, to handle such a complex problem, they imposed very strong assumptions on the considered VSP (no interlining, no deadheading) which turn the problem in an unrealistic one.
In this paper, we address the VSP with trip shifting and limited alteration of the timetable quality for a bus company towards reducing fixed and variables costs. The main idea is to better utilize the resources, introducing small changes in the timetabling, allowing a smaller cost final scheduling. We present an integer linear programming model to integrate the timetable generation process and the vehicle scheduling with heterogeneous fleet based on a Time- Space Network (TSN). Specifying, timetable generation consists in modifying a current timetable, ensuring better distribution of trips and quality services to passengers. In order to modify the timetable, two approaches are applied: time windows and aggregated trips. We tested our program in large random instances based on real instances of a public Brazilian transportation system, where the timetable presents irregular headways, i. e., buses departure time do not have a fixed interval (e. g., a departure every 10 minutes), which provides a better matching of the proposed models and appropriate modification of timetabling.
The major contributions of this paper to the literature are as follows: (i) to model the vehicle type scheduling problem in situations where departure flexibility can be considered; (ii) a simple and efficient implementation of time windows by a small modification in the traditional time-space underlying network, allowing its solution by commercial software in reasonable time; and (iii) to use the demand as a parameter to solve the VTSP, an overlooked parameter in the literature about public transportation optimization. To the best of our knowledge, the integrated formulation and solution comprising the VTSP and timetable generation, based on a TSN have not been previously published.
2.MODELING THE PROBLEM
In order to solve the problem, we applied the well-known Operations Research methodology, consisting of the following steps: (i) Problem Formulation; (ii) Modeling the problem; and (iii) Experimentation. The problem consists of integrating the timetabling and the vehicle scheduling problem towards better utilization of the resources, and consequent minimization of fixed and variable costs. By means of trip shifting and redundant trips deletion, and selecting buses with sufficient capacity to transporting the previously known demand in the ∆t interval which the trips belong to, we expect to optimize the timetabling based on the type of vehicles scheduled, creating an integration of these two complicated tasks.
The models developed in this paper are based on a TSN structure, firstly described for the VSP in Kliewer (2002) and subsequently applied by Kliewer et al. (2006); Kliewer et al. (2012) and Steinzen (2010). Beforehand, VSP was traditionally formulated using a connection-based network (Carpaneto, 1989). The main advantage of the TSN structure is the reduced number of variables and constraints, compared with the traditional connection-based network. Steinzen et al. (2010) showed a comparison between the number of deadhead arcs plotted on a TSN and on a connection-based network and concluded that if the problem contains m stations and n trips, then the number of dead- head arcs in a TSN is O(mn) in opposite to 0(n2) of the connection-based network, with 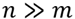 . They also point out that TSN is especially relevant when the number of stations involved in the problem is low when compared to the number of trips; such situation occurs in this paper.
. They also point out that TSN is especially relevant when the number of stations involved in the problem is low when compared to the number of trips; such situation occurs in this paper.
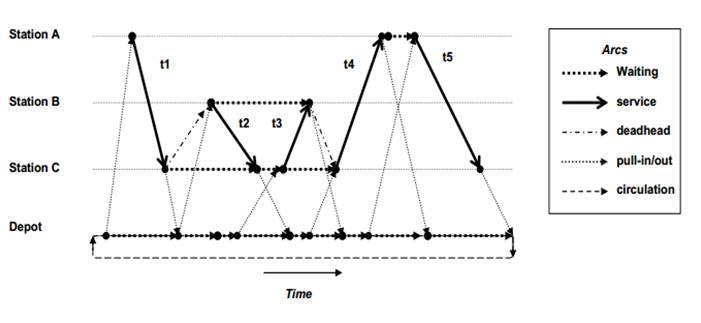
This network is composed by an acyclic directed graph G = (N, A) with N as the set of nodes, which represent a specific location at time, and A as the set of arcs, which corresponds to a transition in time and, possibly, space. The set A is divided into five subsets and a circulation arc (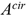 ):
):
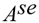 is the set of service arcs, used to connect the corresponding departure and arrival nodes at the start and end locations of a trip with passengers
is the set of service arcs, used to connect the corresponding departure and arrival nodes at the start and end locations of a trip with passengers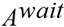 is the set of waiting arcs, representing transitions in time-space network where the vehicles is waiting at a station.
is the set of waiting arcs, representing transitions in time-space network where the vehicles is waiting at a station. is the set of deadhead arcs, where the vehicles move without passengers between two compatible trips from the end location of the first trip to the start location of the second one.
is the set of deadhead arcs, where the vehicles move without passengers between two compatible trips from the end location of the first trip to the start location of the second one. is the set of pull-in arcs, expressing the arcs from the depot to a station to start a trip.
is the set of pull-in arcs, expressing the arcs from the depot to a station to start a trip. is the set of pull-out arcs and represents the arcs from a station toward the depot, when a vehicle returns to the depot for each trip.
is the set of pull-out arcs and represents the arcs from a station toward the depot, when a vehicle returns to the depot for each trip.
Figure 1 exemplifies a network with one depot and three stations. The service, deadhead and pull-in/out arcs denote the bus in movement while waiting arcs represent the bus stopped at a station. This example considers one vehicle type (for a heterogeneous fleet, the network has a multi-layer structure, with one layer for each vehicle-type). It is interesting to note that this example introduces a set of circulation arcs, Ac, connecting the last node (in time) of the depot to its first node, representing a daily schedule for each vehicle type (Steinzen et al., 2010).
The idea of TSN is to exploit the transitivity property of partial ordered sets which says that for trips p, q, v the following conclusion applies (Bunte, and Kliewer, 2009):
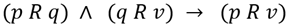 , being 𝑅 a binary relationship.
, being 𝑅 a binary relationship.
This property is easily seen in TSN when preprocessing techniques are applied to generating a small number of arcs in the network structure. The preprocessing techniques has a significant impact on the number of variables and constraints of the mathematical formulation (Kliewer et al., 2002; Kliewer et al., 2006; Van den Heuvel et al. 2008).
In order to consider the heterogeneous fleet, we constructed one network layer for each vehicle type. The networks overlay by vehicle type enables a service trip can be in multiple layers, and hence these layers cannot be solved independently, featuring the VTSP as a multicommodity flow problem. Consequently, the problem becomes NP-hard (Van den Heuvel et al., 2008; Even and Itai, 1976; Bertossi, Carraresi, 1987).
3. MATHEMATICAL FORMULATION
Towards better resource utilizations, we suggest the integration of two operational problems: the timetable generation and the vehicle scheduling problem (with heterogeneous fleet). Thus, given a set of trips with a fixed planning horizon, the model minimizes the total scheduling cost and/or the total number of vehicles. Based on the VTSP presented by Schmid and Ehmke (2015), the proposed model aimed to minimize the total number of vehicles, considering the heterogeneous fleet, while it modified simultaneously the current timetable. Given the different capacities of vehicles, model (a) allows choosing the most appropriate vehicle type for each trip; (b) readjusts the timetable to the historical demand and (c) minimizes operating costs. We define the model as Vehicle Type Scheduling Problem with Sequential Change of Timetable (VTSP-SCT), since it simultaneously modifies the timetable from a sequential grouping of trips and schedules the vehicles.
In order to be able to adjust the timetable, we define a time interval 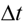 in minutes, and analyze all service arcs (service trips) with departure times coming, with a maximum difference equal to the value of
in minutes, and analyze all service arcs (service trips) with departure times coming, with a maximum difference equal to the value of 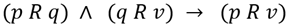 . This time interval is few minutes to ensure the service quality for passengers. The trips inserted in the
. This time interval is few minutes to ensure the service quality for passengers. The trips inserted in the 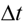 intervals must have the same station of departure and destination. The objective of this approach is to delete redundant trips of timetable and select buses with sufficient capacity to transporting the previously known demand in the
intervals must have the same station of departure and destination. The objective of this approach is to delete redundant trips of timetable and select buses with sufficient capacity to transporting the previously known demand in the 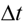 interval which these redundant trips belong to. As intervals are of a few minutes, the model just removed from the timetable trips which time departure is very close, not affecting the quality of service to passengers.
interval which these redundant trips belong to. As intervals are of a few minutes, the model just removed from the timetable trips which time departure is very close, not affecting the quality of service to passengers.
The trips are considered in sequence aiming to identify which trips can be grouped within 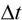 , from the first trip departure of the day towards the departure time of the last trip. Algorithm 1 describes the generation of trip intervals on VTSP-SCT considering, for a station s,
, from the first trip departure of the day towards the departure time of the last trip. Algorithm 1 describes the generation of trip intervals on VTSP-SCT considering, for a station s, 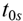 as the departure time of the first trip of the day, and
as the departure time of the first trip of the day, and  as the departure time of the last one. Still,
as the departure time of the last one. Still,  corresponds to the set of service trips belonging to the time interval with index k
corresponds to the set of service trips belonging to the time interval with index k 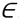 K. The sets
K. The sets 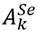 on VTSP-SCT are mutually exclusive.
on VTSP-SCT are mutually exclusive.
The VTSP-SCT, based on the TSN, can be formulated considering each trip represented by two nodes connected by an arc, defined by a graph G = (N, A), with N as the set of nodes and A the set of arcs. Let F the set of different vehicles type, K the set of intervals of index k, 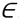 the set of service trips,
the set of service trips,
 the set of service trips belonging to the intervals of index
the set of service trips belonging to the intervals of index 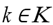 . The parameters are:
. The parameters are:  , the capacity of vehicle type
, the capacity of vehicle type 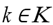 and;
and; 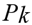 the total demand of the intervals of index
the total demand of the intervals of index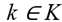 . The binary decision variable
. The binary decision variable 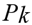 is equal to 1 if the arc (i, j) is performed by vehicle type
is equal to 1 if the arc (i, j) is performed by vehicle type 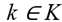 and; 0 otherwise. Finally,
and; 0 otherwise. Finally, 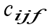 is the cost of vehicle type
is the cost of vehicle type 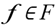 travels by arc
travels by arc 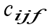 . The mathematical formulation for the VTSP-SCT is represented as follows:
. The mathematical formulation for the VTSP-SCT is represented as follows:
st
The objective function (1) minimizes the total vehicle costs. Constraint (2) ensures the conservative flow properties of the network, while constraint (3) ensures that the capacity of the vehicles that will perform trips inserted in the interval of index k is greater than the total demand of the interval. Constraint (4) ensures that all trips are operated exactly once for a single vehicle type. Constraint (5) and (6) are domain constraints of the decision variable 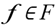
Additionally, by including time windows in the VTSP- SCT, we allow to shift scheduled trips within defined interval, i.e., we introduce more flexibility in the departure times of trips, increasing operational advantages on the number of required vehicles. When considering heterogeneous fleet, time windows become even more useful since the timetabling can be slightly redefined according to the demand and the bus type assigned to cover it. Thus, we developed new time windows arcs implementation directed to heterogeneous fleet.
Kliewer and Mellouli (2006) and Desfontaines and Desaulniers (2017) implemented time windows for homogeneous fleet in the context of multi-depot vehicle scheduling problem (MD-VSP) and integrated MDVSP and crew scheduling problem, respectively. In both papers, with small time windows (few minutes), they made minor modifications in the timetable by shifting some trips. Based on a TSN structure, they insert time window arcs, which are multiplications of original service trip arcs, representing a trip displacement of a certain amount of time and generating a network with a huge number of arcs. Due to the size network and complexity they developed a preprocessing routine to filter out useless arcs and two heuristic approaches to identify the critical set of trips and solve the problem faster were developed. In order to solve the VSTP- SCT, a NP-hard model, we developed a new implementation of time windows, based on Kliewer and Mellouli (2006) and Desfontaines and Desaulniers (2017), but with a smaller size network because time window arcs generated in a similar way to the waiting arcs, instead of multiplying the original service arcs.
The basic idea of the new implementation is to shift some trips of a given timetable and modify possible departure and arrival times. Time window arcs assumed discrete values. The computational implementation is easy and corresponds to add time window arcs linking two trips from the same station, since they are within the defined time window (usually 1 or 2 minutes). The time window arcs are expressed in the network like “reversed waiting arcs”, i. e., waiting arcs implemented with an inverse direction. Since the resulting TSN creates few new arcs, the approach enables the use of large instances as well as integration with the VTSP-SCT. The Algorithm 2 explains how to add time window arcs, considering j an arrival node, i a departure node,  an arrival time,
an arrival time, 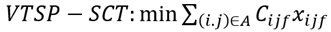 a departure time and
a departure time and 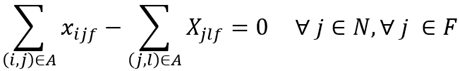 the time window parameter (in minutes).
the time window parameter (in minutes).
In order to allow a consistent and adjusted timetable and avoid the accumulation of successive time window arcs, which could result in successive delays on the optimal solution, we added to the model (1) - (6) a constraint (7), which requires that whenever there is flow in a time window arc, there must be a flow in a waiting arc that immediately precedes the service trip performed. The size, in time, of each respective waiting arc should be at least equal to the time window arc. Another case consists in avoiding that different vehicles types use time window arcs in sequential trips, leaving the timetable very disturbed and probably increasing the enabled time window. To include correct time window arcs, we define the constraint (8). Let 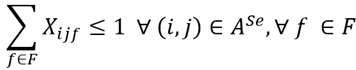 the set of time window arcs, constraints (7) and (8) can be represented by:
the set of time window arcs, constraints (7) and (8) can be represented by:
We applied penalty costs to each time window arc to ensure that they only take place if savings are obtained, as well as for minimizing changes to the original timetabling. Small time windows intervals enable few changes at the original timetabling, ensuring the service level and the passenger’s satisfaction.
4. EXPERIMENTAL RESULTS
The model was coded in C++ and all tests were performed on an Intel Xeon CPU E5-1603 with 2,8 GHz, 16 GB of memory. We used IBM ILOG CPLEX Optimization Studio V12.5. for computing the solutions. For the computational tests, we used large random instances generated based on real instances. Table 1 shows the instances characteristics with its respective configuration (Configuration), number of trips (#Trips) and number of stations (#Stations). For each one of random instances configurations five instances and their average corresponds to the results for each configuration were generated. The demand for the random instances are based on historical demand of the public transit companies analyzed, resulting in minimum number of passengers equal to 20 and maximum number equal to 110.
Table 1 Instances characteristics
| Configuration | # Trips | # Stations |
|---|---|---|
| 1000 10 | 1000 | 10 |
| 1000 23 | 1000 | 23 |
| 3000 10 | 3000 | 10 |
| 3000 23 | 3000 | 23 |
| 5000 10 | 5000 | 10 |
| 5000 23 | 5000 | 23 |
In all instances, the heterogeneous fleet is composed by three different vehicle types as follows: type A, corresponding to an articulated bus, with capacity for 141 passengers; type B, the most commonly used type, with capacity for 100 passengers; and type C, a smaller vehicle able to carry up to 83 passengers. For each vehicle type is defined a cost multi- plication factor directly proportional to the capacity of the bus. We considered the costs as a sum of fixed and variable costs, where variable costs reflect operating time outside the depot and distance covered. To service, deadhead and pull-in/out arcs we regard the sum of operating time and distance costs while only operating time costs are considered for waiting arcs outside the depot. We overestimated the circulation arcs to find the minimal number of vehicles. The computational time for each test is limited to 7200 seconds.
The results for the VTSP-SCT for random instances with and without time windows are presented in Table II and intended validate the model and identify its behavior for large instances. Still, we compare the number of scheduled vehicles in this approach with those scheduled by the VTPS (without modification of the timetable). Computational tests were performed for 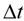 = 1, 2 and 3 minutes, and time windows
= 1, 2 and 3 minutes, and time windows  = 1 and 2 minutes. Column “Vehicles” indicates the number of vehicles scheduled for each bus type, column “Shifted Trips” refers to the number of trips eliminated from the timetable and “Active TW” the time window arcs applied.
= 1 and 2 minutes. Column “Vehicles” indicates the number of vehicles scheduled for each bus type, column “Shifted Trips” refers to the number of trips eliminated from the timetable and “Active TW” the time window arcs applied.
All instances were solved at optimality in lower time than the established limit (7200 seconds). With the exception of instance 1000_23 to 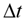 = 1 in all the other instances VTSP- SCT led to higher savings than the VTSP model. For instances with 1000 trips, the number of reduced vehicles was lower than in other instances, grouping a small number of trips and activating few time windows. This result is expected, because the number of trips is reduced in this instance if compared with the other ones; thus, the distribution of trips is farther away, which difficult the grouping of trips at short
= 1 in all the other instances VTSP- SCT led to higher savings than the VTSP model. For instances with 1000 trips, the number of reduced vehicles was lower than in other instances, grouping a small number of trips and activating few time windows. This result is expected, because the number of trips is reduced in this instance if compared with the other ones; thus, the distribution of trips is farther away, which difficult the grouping of trips at short 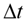 intervals. Furthermore, instances with 23 stations tend to group less trips, due to dispersion between trips departure times, preventing most of intervals of index k.
intervals. Furthermore, instances with 23 stations tend to group less trips, due to dispersion between trips departure times, preventing most of intervals of index k.
Specifically, the results for the instance 3000_10 show the advantages of using the integrated VTSP-SCT with time windows. For these results, the total number of vehicles is substantially reduced by enabling compatibility of trips through time window arcs. Considering that the number of grouped trips in this instance is quite high, the application of time windows enables to obtain a better utilization of vehicles without modifying too much the timetable, which tends to contribute to maintaining the quality of service provided to passengers.
For the instance 5000_10 we note the largest economy of vehicle numbers compared to the VTSP model. With 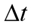 = 3 minutes, for this instance, the number of vehicles reduces, on average, in 20 units if compared with VTSP. Such results indicate that allowing a larger bus type (Type A) on a trip gives a high cost reduction and significantly reduces the number of buses used. The application of time windows generates even more savings without excluding trips of timetable. Instance 5000_23 generated results with higher resolution time, on average. It is an expected result given the high number of trips and stations of this instance. In addition, we could see a fairly common behavior of the model VTSP-SCT: the increasing of time resolution for wider ∆t intervals due to numerous possibilities for grouping. However, high computational times for larger instances do not preclude the practical application of this model, considering the savings obtained, allowing the reduction of a large number of vehicles. Moreover, considering the fact that many managers still scheduling vehicles manually, a task with quite time consuming, the period of 1 to 2 hours for a computational resolution becomes reasonable.
= 3 minutes, for this instance, the number of vehicles reduces, on average, in 20 units if compared with VTSP. Such results indicate that allowing a larger bus type (Type A) on a trip gives a high cost reduction and significantly reduces the number of buses used. The application of time windows generates even more savings without excluding trips of timetable. Instance 5000_23 generated results with higher resolution time, on average. It is an expected result given the high number of trips and stations of this instance. In addition, we could see a fairly common behavior of the model VTSP-SCT: the increasing of time resolution for wider ∆t intervals due to numerous possibilities for grouping. However, high computational times for larger instances do not preclude the practical application of this model, considering the savings obtained, allowing the reduction of a large number of vehicles. Moreover, considering the fact that many managers still scheduling vehicles manually, a task with quite time consuming, the period of 1 to 2 hours for a computational resolution becomes reasonable.
Computational experiments for the VTSP-SCT indicate the reduction of the operational costs, represented by the minimization of vehicle numbers in a lower computational time, mainly for large instances (above 1000 trips). It seems that the number of stations is not so relevant as the number of trips, based on the results of instances with 5000 trips. Only for very large instances, the use of trip shifting increases the CPU time to find optimal solutions, doubling the required CPU time, but the benefit of decreasing the number of vehicles compensates this effect. Reductions of around 3% in the number of vehicles were obtained with model VTSP-SCT. For instance 5000_10, a reduction of 20% was obtained when a greater flexibility in the timetabling was allowed. A considerable economic saving can be consequence of this reduction, if we consider additional costs such as drivers and maintenance. Overall, bssed on the overall results, we showed the suitability of time window integration to VTSP-SCT, a feature that increases the scenarios to be evaluated by transit operator’s manager to schedule different types of vehicles and enables more flexibility to define the new timetabling.
5. CONCLUSION
In this paper, we propose a new approach to solve vehicle- type scheduling problem (VTSP), which comprises the integration of the vehicle scheduling problem and the vehicle type required for each trip, keeping a certain level of service for each trip such as the degree of passengers’ comfort, seat availability, and other operational features. The VTSP-SCT is an integer linear programming (ILP) aiming at optimizing the VTSP and the timetabling generation problem based on a time-space network (TSN). Additionally, we developed a new methodology to insert time window to the proposed problem, based on small changes in the TSN structure, with easy computational implementation and optimal solution at low computation run-times.
The time window proposed approach is based on the implementation suggested by Kliewer and Mellouli (2006) and Desfontaines and Desaulniers (2017) with some differences: our computational implementation do not need preprocessing to delete unused time-window arcs and time window arcs are generated in a similar way to the waiting arcs, instead of multiplying the original service arcs. As a result, a smaller size network is generated. By having a smaller number of nodes and arcs, the new approach facilitates the integration with the VTSP-SCT, a problem with a large number of variables and constraints.
By including small changes to the timetable and/or including time windows for timetabling trips, we introduced flexibility levels in the departure times of trips, resulting in operational advantages for the service provider. Since we applied a very short time window interval, the current timetable was only slightly modified, minimally changing the passenger routines. The developed approaches were tested using random instances based on a Brazilian city, where the timetable presents irregular headways, in which the buses departure time do not have a fixed interval. The VTSP-SCT with and without time windows have resulted in relevant savings in the daily operations of the public transportation service, reducing the required number of scheduled vehicles to carry out the historic demand.
We intend to apply this new approach in order to solve multiple-depot vehicle scheduling problems (MDVSP) and integrated vehicle and crew scheduling problem (IVCSP), considering heterogeneous fleet.