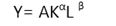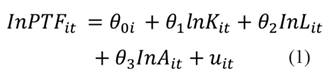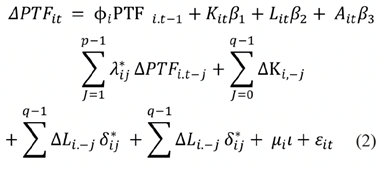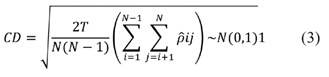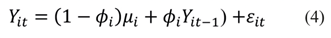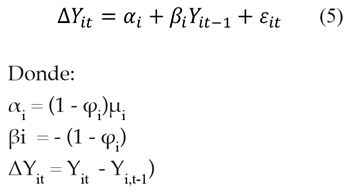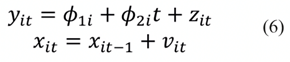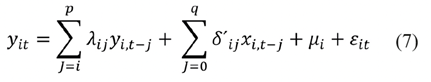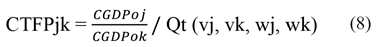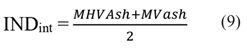Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Contexto latinoamericano
El lento crecimiento económico es un problema que ha caracterizado a América Latina, de acuerdo con datos del Banco Mundial (2023), desde la década de los noventa los países que integran esta región, han tenido un crecimiento porcentual de su Producto Interno Bruto (PIB) del 2.5 %, por debajo del promedio mundial, que para estos años fue del 2.9 % anual. Esta situación puede ser atribuida a una serie de factores de corte estructural, sin embargo, también se asocia a la eficiencia de las economías y a su productividad (CEPAL, 2016).
El crecimiento de la actividad económica se encuentra correlacionado con la productividad, en el contexto latinoamericano esta situación ha revelado un atraso lo que limita el desarrollo de estos países. El análisis de la Productividad Total de los Factores (PTF) representa un elemento fundamental para las economías con ingresos medios, ya que explica una parte del rezago al cual se enfrentan, diversos autores identifican que es a través de la mejoría en la eficiencia productiva donde podrán cerrar la brecha en la distribución del ingreso (Kim y Park, 2017; Yalçınkaya et al., 2017).
En América Latina existe una gran limitante asociada con la informalidad de la economía, los trabajadores no cuentan con acceso a seguridad social afectando directamente su productividad, las empresas se encuentran al margen del cumplimiento de sus obligaciones fiscales lo que limita el acceso al financiamiento (Aravena y Fuentes, 2013; Ros, 2008), este factor que ha caracterizado a la región incide en el desempeño de los factores de la producción, y por consiguiente en la PTF.
Adicionalmente se considera que el avance tecnológico en la región, elemento que tendría que ser fundamental para lograr el crecimiento económico, no ha tenido un papel clave en el desenvolvimiento de la PTF, este hecho es evidenciado a la luz de un número limitado y por debajo de la media mundial de solicitudes de patentes (Banco Mundial, 2023c), y una escasa inversión en I+D (Banco Mundial, 2023b), demostrando la ineficiencia técnica de las economías protagonistas de este artículo que limitan el desarrollo de su PTF, lo que incide de manera negativa en su crecimiento económico.
Fundamentos
En este trabajo la PTF tiene un papel preponderante ya que es un indicador macroeconómico que se encuentra enmarcado en la contabilidad del crecimiento, el cual identifica el desempeño de los factores de la producción trabajo (L), capital (K) y el cambio tecnológico (A) como determinantes de la producción en el sentido de Cobb-Douglas (1928), es así, que su análisis resulta de gran utilidad para la aplicación de medidas de política económica (Barro y Sala-i-Martin, 2012).
El objetivo de este trabajo es analizar el comportamiento de los factores de la producción en el desarrollo de la PTF para las economías latinoamericanas durante el periodo 1990-2019. El primer aporte de esta investigación se encuentra relacionado con el uso del estimador del Grupo de Medias Agrupadas propuesto por Pesaran et al. (1999), el cual permite estimar los coeficientes de largo plazo y los coeficientes de corrección de error, al tiempo que genera los coeficientes específicos de corto plazo, lo anterior mediante una estimación de máxima verosimilitud. El segundo aporte que tiene la investigación es que se prueba la hipótesis de que el trabajo, el capital, así como el cambio tecnológico han sido los determinantes de la PTF de las economías latinoamericanas durante el periodo 1990-2019, esto a partir de la función de producción Cobb Douglas.1
Este trabajo se divide en seis apartados. En el primero se tiene la introducción. El segundo corresponde a la revisión de la literatura, específicamente se trabaja la función de producción y los modelos de crecimiento. En el tercero se da la evidencia empírica de las variables. En el cuarto, se desarrolla la metodología y las bases de datos. Los resultados se presentan y son analizados en el quinto apartado. Finalmente, en el sexto apartado se presentan las conclusiones derivadas de este estudio.
Revisión de literatura
Desde sus inicios, la ciencia económica ha tenido como objetivo analizar el crecimiento de los países, así como sus diferencias, desde la perspectiva neoclásica es posible abordar los elementos que son determinantes en la producción de un país, a partir del desempeño de los factores de la producción, es decir, del trabajo y del capital, así como del cambio o avance tecnológico, es por ello que en este apartado se realiza un análisis de las teorías que han explicado estas disparidades, tomando como base la función de producción Cobb-Douglas (1928).
Función de producción Cobb-Douglas
Los antecedentes de la función de producción se encuentran, por un lado, en la teoría de Clark (1899) y Wicksteed (1894), los cuales proponen que a partir de la combinación de los factores trabajo y capital es posible determinar el tamaño de la producción. Por otro lado, se tiene la influencia de Wicksell (2001), quien destaca la importancia de analizar los ciclos económicos, identificando que son afianzados a partir de una fuerza externa, la cual denominó progreso técnico. Más tarde, Cobb y Douglas (1928), realizan una contribución fundamentada en la evidencia empírica de la economía de Estados Unidos.
En su trabajo Cobb y Douglas (1928), presentan a partir de la información de la industria manufacturera de los Estados Unidos la función de producción neoclásica, expresada en los siguientes términos:2
donde:
Y= Producción.
A= Progreso tecnológico o PTF.
K= Stock de capital o factor capital (conjunto de bienes o activos que se usan para producir).
L= Número de trabajadores o factor trabajo.
α = Parámetro que indica la capacidad productiva del factor capital.
β= Parámetro que indica la capacidad productiva del factor trabajo.
Los parámetros indican la tasa de cambio que ejerce el trabajo o el capital en la producción de la industria manufacturera, de manera que la primera derivada indica la proporción de la variación que los factores tienen en el crecimiento de la producción, es decir, se presenta la productividad marginal del capital (α) y del trabajo (β).
Cobb y Douglas (1928), consideran en su artículo que existen rendimientos constantes, esto es, la suma de los parámetros es igual a 1, no obstante, existen otros casos como los rendimientos decrecientes, donde al sumar los parámetros se obtiene un resultado inferior a la unidad, mientras que si fuera mayor que 1 se clasificaría como rendimientos crecientes a escala. El resultado al cual llegan Cobb y Douglas (1928), establece que la producción, el trabajo y el capital se encuentran relacionados, de tal manera que, si se multiplican estos dos últimos por un factor , la producción se incrementa en esa cuantía, es decir en m veces, esto es, la producción es una función homogénea de primer grado del trabajo y del capital.
El resultado al cual llegan Cobb y Douglas (1928), se encuentra en congruencia con la función de producción de Clark (1899) y Wicksteed (1894). Los autores consideran que es posible realizar la cuantificación a partir del método de Mínimos Cuadrados Ordinarios (MCO), con este aporte a la teoría económica presentan una propuesta innovadora en los estudios del crecimiento económico.
Modelos de crecimiento
En el marco del enfoque neoclásico, existen diversas perspectivas que explican el crecimiento económico. Por un lado, se encuentran aquellas teorías que identifican el crecimiento de una manera exógena, esto es, las variables que explican el crecimiento económico se encuentran fuera del modelo, además se fundamenta la idea de que una vez encontrado el estado estacionario la relación capital-producto no varía, obteniendo así una relación fija, esto implicaría que en el largo plazo la actividad productiva se encuentra limitada por factores exógenos tanto de lado de la oferta como de la demanda (Perrotini et al., 2019). Por otro lado, existen teorías que determinan que la tasa de crecimiento no se encuentra en estado estacionario, por lo tanto, se tendría que incentivar el capital humano, así como las capacidades y habilidades de este, lo que conduciría a una mejoría en el factor tecnológico (Jiménez, 2011).
Durante la década de los cincuenta hasta los años noventa predominó el pensamiento de los modelos de crecimiento exógeno que identificaron el llamado estado estacionario, donde los factores de la producción trabajo y capital no provocan un aumento en el crecimiento de la producción, es decir, provocaban rendimientos decrecientes. Por tanto, una fuerza exógena sería la que causaría esta situación, esto es, a partir de los avances tecnológicos de los países se podría mostrar dicho fenómeno, el principal exponente de esta corriente es Solow (1956). Con su famoso residuo, reconoce que, en el largo plazo, será el aumento en la tasa de ahorro y el avance tecnológico, es decir, las variaciones en la constante A, las que provocarán el crecimiento económico. El modelo de crecimiento óptimo desarrollado a partir de los trabajos de Ramsey (1928) y posteriormente retomado por Koopmans y Cass (1965), muestran desde la perspectiva microeconómica la decisión de los hogares y las empresas entre el ahorro y el consumo, y como dicha situación afectará el bienestar intertemporal y el crecimiento económico retoman la idea del avance tecnológico de manera exógena.
El modelo de crecimiento de Mankiw et al. (1993), retoma las ideas del residuo de Solow identificando que dicho autor estaría en lo correcto al considerar los factores de la producción, no obstante, se tendría que dar un mayor peso al factor trabajo ya que será la fuerza trabajadora quien, a través de sus habilidades y conocimientos, genere un cambio en el crecimiento económico. En resumen, los modelos de crecimiento exógeno identifican que, en el largo plazo, la única manera de generar un aumento en la producción será si se implementan mejoras tecnológicas.
Durante la década de los noventa, los estudios económicos muestran un fuerte rechazo al llamado estado estacionario, logrando de esta manera, endogeneizar las variables que permiten lograr un crecimiento de la producción. De acuerdo con diversos autores el papel de los trabajadores será decisivo y, no proviene de manera foránea o externa debido a que es este factor ya sea mediante la adquisición de conocimientos y habilidades, o por las externalidades positivas generadas por la I+D que incrementa su productividad y por consiguiente, el crecimiento económico de una manera sostenida (Romer, 1986; Baumol, 1986; Lucas, 1988). Adicionalmente existen otros trabajos que identifican la importancia del gasto público y de las inversiones en I+D, así como de la estabilidad en las políticas monetarias y fiscales y el papel de las instituciones como elementos que propician el crecimiento económico (Barro, 1991; Rebelo, 1991; Howitt, 2004).
En síntesis, los modelos endógenos consideran que, para lograr el crecimiento económico de manera sostenida es necesario incentivar el capital humano, y esto será posible a través de la inversión en I+D, ya que genera externalidades positivas, como el incremento de la productividad en este factor. Dicho de otro modo, será posible tener rendimientos crecientes o constantes a escala, conjuntamente se resalta el papel de las instituciones y de la estabilidad macroeconómica para lograr la expansión económica de los países.
Evidencia empírica
La revisión de la literatura permite identificar algunos aspectos de la PTF en diversos contextos, en este sentido, existen trabajos que consideran el papel que ha tenido la PTF en el crecimiento económico (Hofman et al., 2017; Kim y Park, 2017; Villalobos et al., 2021; Yalçınkaya et al., 2017). Otros estudios se enfocan en cuantificar la aportación de los factores de la producción en el crecimiento de la PTF (Ayvar y Guitrón, 2013; Maudos et al., 1999; Nguyen, 2021; The Conference Board, 2023). Adicionalmente hay evidencia empírica que analiza el impacto en la PTF de otras variables tales como, los desequilibrios macroeconómicos, los términos de intercambio, las volatilidades en el comercio o la importancia en la I+D (Dańska-Borsiak y Laskowska, 2012; Gutiérrez Villca, 2020; Méndez et al., 2013).
En los estudios que tienen como objetivo estudiar la influencia que tiene la PTF en el crecimiento económico, es posible generalizar las similitudes que existen en los resultados a los cuales llegan diversos autores que revelan la importancia que tiene la PTF, incluso por encima de los factores de la producción trabajo y capital en el crecimiento económico (Kim y Park, 2017; Yalçınkaya et al., 2017). Los estudios latinoamericanos dan evidencia en este sentido, ya que presentan contribuciones negativas en el crecimiento de la PTF, siendo esto una consecuencia y explicación para el escaso crecimiento económico (Hofman et al., 2017; Méndez et al., 2013; Villalobos et al., 2021).
Los trabajos que analizan la aportación de los factores de la producción consideran, por un lado, que el factor trabajo o capital humano influye de manera más significativa en la PTF (Ayvar y Guitrón, 2013; Maudos et al., 1999), mientras que para otros estudios es el factor capital el que tiene mayor incidencia en la PTF (Nguyen, 2021; The Conference Board, 2023) por supuesto que estos resultados deben ser considerados para diferentes economías en diversos contextos.
Existen estudios latinoamericanos, no enmarcados en el enfoque de la función de producción que consideran variables que explican el comportamiento de la PTF. Por una parte, se tiene los estudios que relacionan de manera directa la PTF con la eficiencia técnica, el progreso tecnológico, los términos de intercambio, Inversión Extranjera Directa, el ahorro, la productividad media por trabajador, la escolaridad y la esperanza de vida (Gutiérrez, 2020; Méndez et al., 2013; Ramírez y Aquino, 2005). Por otra parte, Gutiérrez (2020) encuentra una relación negativa de la PTF con los desequilibrios macroeconómicos, la volatilidad en el comercio, la informalidad, la tasa de fertilidad, la desigualdad y crisis externas. Finalmente, Ramírez y Aquino (2005), dan evidencia de una relación inversa entre las crisis inflacionarias y la PTF.
Los trabajos revisados enfatizan la importancia de la variable I+D, ya que serán los esfuerzos en el progreso tecnológico los que causen el incremento en la PTF, y con ello generarán mayor crecimiento económico (Dańska-Borsiak y Laskowska, 2012; Méndez et al., 2013; Nguyen, 2021).
Estudios más recientes analizan el comportamiento de las economías de Asia Oriental, a través de metodologías de datos de panel, adicionando otros elementos, en los cuales se destacan: la inversión real, la acumulación de capital físico, el número de horas promedio de trabajo, el desarrollo del capital humano, así como la tasa interna de retorno como factores clave en el crecimiento de la PTF (Lee y Viale, 2023). El trabajo realizado por Rehman e Islam (2023), se enfoca en las economías de los BRICS y destaca la importancia de la infraestructura financiera tanto en el corto como en el largo plazo, la apertura comercial, la IED, el capital humano, la innovación y la calidad institucional como factores que inciden en la PTF.
En otro enfoque de estudios, se destaca la importancia de la PTF verde (GTFP, por sus siglas en inglés), como una medida de eficiencia orientada a la sostenibilidad ambiental. Es decir, por un lado, se consideran los factores tradicionales de la producción, y por otro, se integra el impacto al medio ambiente, promoviendo enfoques de corte más sostenible, este tipo de trabajos tienen mayor aplicación en la economía China (Jiakui et al., 2023; H. Liu et al., 2023; Y. Liu et al., 2023). En la misma línea, existen trabajos donde se analiza la incidencia de la tecnología digital (Pan et al., 2024), las finanzas verdes (flujos financieros destinados a proyectos sostenibles) (Feng et al., 2024; Yue et al., 2024), así como el desarrollo del internet y la banda ancha móvil en la determinación de la PTF verde (Edquist, 2024; Wen y Deng, 2024).
Materiales y métodos
En esta investigación, los modelos de crecimiento son analizados mediante la metodología de datos panel, se han tomado en cuenta los beneficios que tienen este tipo de modelos comparados con un modelo típico de corte transversal o, inclusive, también serían capaces de controlar la heterogeneidad individual e identificar los efectos que habrían sido indetectables en datos de series de tiempo tradicionales.
En este trabajo la especificación empírica del modelo de datos panel queda como sigue:
Donde el representa el promedio de las variables en el largo plazo, de tal suerte que el logaritmo de la PTF se encuentra en función del logaritmo del factor capital (K), en segundo lugar, se considera el logaritmo del factor trabajo y por último la PTF está definida por el cambio tecnológico y es el término de error.
Como lo especifican Pesaran et al. (1999), es posible llevar a efecto una reparametrización con la finalidad de realizar una estimación PMG, quedando la ecuación en los siguientes términos:
donde:
ϕi: = Parámetro de velocidad de corrección de errores del término de ajuste.
PTFit= Vector de T x 1 de las observaciones de la variable dependiente en las economías latinoamericanas.
Kit= Matriz de T x k de observaciones sobre los regresores de la variable independiente capital que varían entre grupos en el periodo de tiempo.
Lit= Matriz de T x k de observaciones sobre los regresores de la variable independiente trabajo que varían entre grupos en el periodo de tiempo.
Ait= Matriz de T x k de observaciones sobre los regresores de la variable independiente cambio tecnológico que varían entre grupos en el periodo de tiempo.
ι = (1,…, 1) es un vector T x 1 de los PTFi,-j, K i-j, L i-j, A i-j son j valores rezagados del periodo de PTFit, Kit, Lit y Ait.
λit = Escalares.
δ= Vectores de coeficientes k x 1.
εi= Término de error.
Prueba de dependencia transversal
Pesaran (2004), propone un estadístico eliminando el método de cálculo que tradicionalmente se había considerado, esto es, la matriz espacial resultaba incompleta para especificar si los datos contaban con dependencia, esta métrica no permitía que se capturasen los factores comunes (económicos o sociopolíticos) que son determinantes y que generan dependencia. La prueba CD de Pesaran (2004), es una rutina válida cuando N y T →∞ bajo cualquier orden.
La toma de decisión para determinar si existe o no dependencia transversal, supone que el término de error uit es independiente e idénticamente distribuido (i.i.d.) a lo largo de los periodos y entre las unidades transversales (Pesaran, 2004).
Prueba de raíz unitaria CADF
Las variables que son observadas a través del tiempo requieren una serie de pruebas que aseguren que son estacionarias “en términos generales, una serie de tiempo es estacionaria si su media y varianza no varían sistemáticamente con el tiempo” (Gujarati y Porter, 2010).
Existe una metodología que permite identificar la raíz unitaria cuando existe dependencia en la sección transversal (Im et al., 2003), de esta manera se relaja el supuesto de independencia transversal que las pruebas de primera generación pugnaban ya que “eran bastante restrictivas y poco realistas en las aplicaciones macroeconómicas” (Hurlin y Mignon, 2006, p. 3).
La prueba de estacionariedad (Im et al., 2003) consiste en aumentar las regresiones estándar con los promedios de sección transversal, a partir de los rezagos y de las primeras diferencias para cada serie teniendo de esta manera promedios simples aumentados transversalmente, lo que resultaría en un nuevo estadístico denominado CADF. El desarrollo del modelo se encuentra especificado a partir de las regresiones estándar de Dickey-Fuller con el promedio de la sección transversal de los niveles rezagados y de las primeras diferencias.
Se considera un modelo para N secciones transversales observadas en T periodos:
El interés resulta en los valores de probando la hipótesis nula de raíces unitarias para todo i (ϕi = 1), lo cual puede ser expresado en la siguiente ecuación:
Cointegración
Los modelos de datos panel tienen la posibilidad de establecer relaciones en el largo plazo lo cual puede ser verificable a través de la prueba de cointegración, tradicionalmente dicho test requería que los parámetros del corto plazo fueran iguales a los de largo plazo, lo que mostraría una falla por poner una restricción de factor común. La prueba propuesta por Westerlund (2007), se encuentra diseñada bajo la hipótesis nula de no cointegración.
El modelo de cointegración desarrollado por Westerlund (2007), puede ser especificado como sigue.
Se considera el siguiente proceso de generación de datos
Donde es un escalar determinístico, el vector es una caminata aleatoria y es el término estocástico. Mientras que t = 1,…,T y i = 1,…,N expresan las series de tiempo y las unidades de sección cruzada respectivamente.
La prueba de cointegración presentada consta de cuatro estadísticos, dos de ellos agrupan la información sobre el error y son denominados estadísticas de panel (Gt y Ga), mientras que los otros muestran las estadísticas (Pa y Pt) de las medias en los grupos, sugiriendo que al menos alguna unidad se encuentra cointegrada (Persyn y Westerlund, 2008).
Estimador de medias agrupadas para paneles dinámicos (Pooled Mean Group)
Tradicionalmente los estimadores para datos panel asumían que los coeficientes y las varianzas de los errores no difirieran entre los grupos, dadas las características de los individuos o unidades económicas, resultaba complejo asumir que en el corto plazo las varianzas del error fueran iguales. Por tal razón, Pesaran et al. (1999), proponen una nueva manera de realizar estimaciones para paneles con N y T grandes a través del estimador para medias agrupadas en paneles dinámicos Pooled Mean Group (PMG), el cual condiciona a los coeficientes en el largo plazo a ser idénticos.
De acuerdo con Pesaran et al. (1999), en el largo plazo se espera que existan relaciones de equilibrio, lo que se expresaría mediante variables homogéneas, o similares entre los grupos. Esto, parecería visible al considerar ciertas condiciones que influyen de manera parecida en el panel, tales como restricciones presupuestales o tecnologías comunes.
Un modelo Autoregressive Distributed Lag Model (ARDL por sus siglas en inglés) es aquel que considera rezagos en las variables o lo que es lo mismo se introducen retardos en las variables de los vectores contemplados (Cho et al., 2023).
Estos modelos tienen como finalidad probar la cointegración de las variables. La propuesta de Pesaran et al. (2001), se realiza a partir de una prueba de límites con la finalidad de encontrar las relaciones en el largo plazo a través de un mecanismo de corrección de error, que permite identificar la dinámica de ajuste de las variables en el corto y largo plazo. El panel está dado por la ecuación:
donde:
Yit = Variable dependiente del grupo i.
xit: = Vector de variables explicativas (regresores) para el grupo i.
μi: = Efectos fijos (los coeficientes de las variables dependientes rezagadas).
λij = Escalares.
δij = Vectores de coeficientes kx1.
Bases de datos y fuentes de información
En este trabajo la Productividad Total de los Factores se recupera de la base de datos del Penn World Table versión 10.0 (University of Groningen, 2021), y se obtiene a través del índice de Törnqvist considerando los precios de los factores que se encuentran implícitos en los precios de los bienes (Feenstra et al., 2015).
La Productividad Total de los Factores se calcula utilizando tasas de Paridad de Poder Adquisitivo de cada país en relación con Estados Unidos; y se expresa de la siguiente manera:
donde:
CTFPjk = Es la Productividad Total de Factores a precios corrientes de cada país j en relación con k. Para k se utilizan los precios de referencia de Estados Unidos.
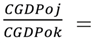Es la variación del PIB a precios corrientes.
Qt (vj, vk, wj, wk) = Es el índice de Törnqvist de la dotación de factores de la producción.
El factor trabajo fue obtenido de la base de datos del Banco Mundial (2023c), y se define como aquellos trabajadores que cuentan con un tipo de empleo remunerado, esto implica que tengan algún contrato (escrito u oral) que garantice su salario.
En el factor capital se utilizó el indicador de servicios de capital, el cual se obtuvo de las bases de datos del Penn World Tabble versión 10. 0 (University of Groningen, 2021). El indicador se obtiene de la siguiente manera: a) a través las existencias iniciales con base en el método de inventarios perpetuos; b) mediante el deflactor de la Formación Bruta de Capital Fijo; c) se incluye el rendimiento del capital en la economía considerando la Tasa Interna de Retorno (TIR) (Inklaar y Woltjer, 2019).
Para la medición del cambio tecnológico, se considera el indicador del grado de intensidad de industrialización como una variable proxy que refleje el cambio tecnológico de las economías latinoamericanas (United Nations Industrial Development Organization, 2013). Haga clic o pulse aquí para escribir texto.
El indicador de grado de intensidad de industrialización (INDint) se obtiene de la siguiente manera:
donde:
MHVash = Es la participación del valor agregado de manufactura de media y alta tecnología en el valor de la manufactura total.
MVash = Es la participación del valor agregado de manufactura en el PIB total (United Nations Industrial Development Organization, 2022).
Resultados y discusión
En este apartado se presentan los resultados de dependencia transversal, de estacionariedad de las series, de cointegración de largo plazo entre los paneles y del proceso de estimación a través de la metodología PMG de Pesaran et al. (1999).
Análisis de dependencia transversal
A través de la prueba CD de Pesaran (2004), se verifica la existencia de la dependencia transversal en las variables estudiadas, los resultados muestran que el valor probabilístico, tanto en la variable dependiente, como en las independientes es 0.000. De acuerdo con la especificación y criterios referidos en el apartado del desarrollo metodológico, la hipótesis nula propone que existe independencia transversal, esta puede ser rechazada lo que permite concluir que existe dependencia transversal. A través de la prueba se obtiene el promedio de los coeficientes de correlación por pares de los residuos de MCO de las regresiones individuales en el panel. Y se puede utilizar para probar la dependencia de la sección transversal de cualquier orden fijo p, así como el caso donde no se asume un orden de las unidades de sección transversal a priori (véase tabla 1).
Prueba de raíz unitaria CADF
Considerando que existe dependencia transversal en las variables estudiadas es posible utilizar las pruebas de raíz unitaria de segunda generación. Con la metodología de estacionariedad (Im et al., 2003), se considera a partir del estadístico CADF los valores críticos consideran que la hipótesis nula de series no estacionarias debe ser rechazada. Se busca que los valores probabilísticos sean inferiores a 0.05, el resumen de la prueba para cada variable y en su primera diferencia puede ser observado en la tabla 2.
Tabla 2 Resultados de las pruebas de raíz unitaria de Pesaran (2003)
Nota. Elaboración propia con base en las estimaciones realizadas en Stata 17.
Las variables cumplen su característica de ser estacionarias en su primera diferencia, por lo que podemos rechazar la hipótesis nula de la no estacionariedad de acuerdo con la prueba de Im et al. (2003), de segunda generación, concluyendo así, que las variables tienen orden de integración uno, I (1).
Análisis de cointegración
La prueba de Westernlund (2007), se basa en la cointegración del panel, si es que ocurre de esta manera, los valores probabilísticos de algunos de los cuatro criterios se encontrarían por debajo de los niveles de significación. En la prueba realizada para las economías latinoamericanas seleccionadas se demuestra que dos de los criterios Gt y Pt son de 0.04 y 0.00 respectivamente, por lo que es posible afirmar que el panel se encuentra cointegrando (ver tabla 3).
El estimador Pooled Mean Group (PMG) para el análisis de la PTF
A través del estimador PMG propuesto por Pesaran et al. (1999), que considera la máxima verosimilitud de coeficientes de largo plazo es posible realizar una agrupación, dadas las condiciones de homogeneidad en los coeficientes. Como lo especifica el autor, a través de un mecanismo de corrección de error es posible determinar que en el corto plazo los coeficientes de las pendientes y las varianzas del error difieran y en el largo plazo sea posible presentar estimadores homogéneos, teniendo los resultados que se observan en la tabla 4.
Tabla 4 Resultados del modelo Pooled Mean Group de Pesaran (1999)
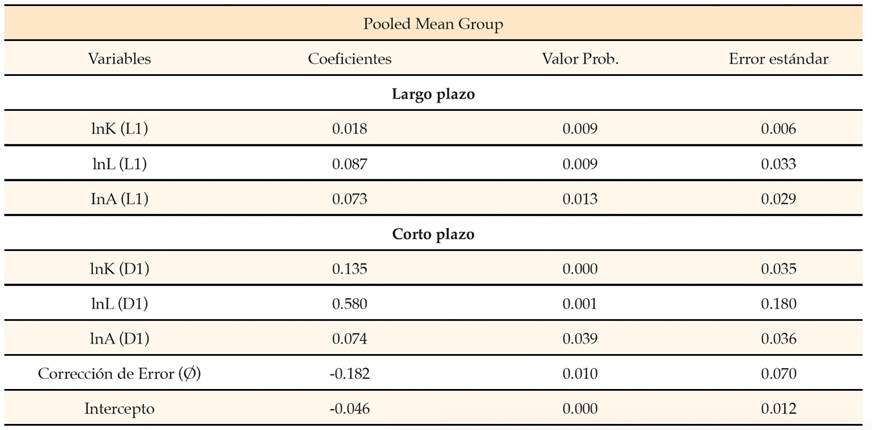
Nota. Elaboración propia con base en las estimaciones realizadas en Stata 17.
El modelo estimado ARDL es de orden (1, 1, 1) dado que la metodología propuesta por Pesaran et al. (1999), el primer 1 supone que existe un modelo que cuenta con un retraso para el cálculo del largo plazo, el segundo hace referencia a la media móvil, y el tercer uno es considerado como la diferenciación de las variables en el modelo, las cuales permiten presentar coeficientes en el corto plazo.
Con base en la evidencia empírica es posible obtener algunas conclusiones respecto a las variables utilizadas. En la parte superior de la tabla en el modelo de largo plazo se encuentran estimadores significativos -los valores probabilísticos son inferiores a 0.05-. La relación entre las variables es la esperada, es decir, se comprueba la hipótesis de trabajo en esta investigación en la que se establece una relación directa entre la PTF y las variables independientes -según la teoría económica neoclásica-.
En el largo plazo ante un cambio de 1 % en la variable trabajo, la PTF se incrementa en 0.0871 % en las economías latinoamericanas seleccionadas en el periodo 1990-2019. La interpretación de este comportamiento da cuenta que ante una mayor formalidad en los empleos y las firmas que apoyan a los trabajadores con servicios médicos, y diversas prestaciones inciden de manera positiva en la PTF. En este sentido, la informalidad y el autoempleo (que serían los trabajadores que no están incluidos en la variable seleccionada de trabajo), son los sectores con productividad más baja, esto es, entre más informalidad y autoempleo exista en los países latinoamericanos menor será la PTF.
Un segundo elemento que se rescata en el largo plazo es el cambio tecnológico, la evidencia empírica revela que, ante cambios unitarios porcentuales de esta variable, la PTF aumenta en 0.073 %, lo que demuestra la importancia de tener un alto grado de intensidad industrial en América Latina. Esto es congruente con la teoría del crecimiento económico propuesta por Solow (1956), que especifica que, en el largo plazo, el progreso tecnológico será determinante para lograr el crecimiento económico.
Por lo que se refiere al factor capital este tiene una elasticidad pequeña, lo que indica que ante un cambio de 1 % en la variable, la PTF se incrementaría en 0.018 %. Esta variable fue la menos representativa en el largo plazo, mientras que el trabajo es la de mayor importancia para las economías latinoamericanas en el periodo 1990-2019.
En la tabla 4 se tiene evidencia además para el corto plazo, en este caso, los estimadores son significativos con valores probabilísticos inferiores a 0.05 y al igual que en el largo plazo se tienen relaciones positivas del trabajo, el capital y el cambio tecnológico respecto a la PTF.
El factor trabajo, presenta un comportamiento similar en el corto y largo plazo, en el sentido de ser la variable que tiene una mayor incidencia en la PTF; sin embargo, se tiene aquí, una mayor elasticidad. Esto es, ante cambios unitarios en esta variable la PTF aumenta en 0.580 %, dando cuenta de la importancia del trabajo formal en las economías estudiadas en esta investigación.
En este caso -corto plazo- el factor capital su importancia es de segundo orden en la determinación del crecimiento de la PTF, se tiene un coeficiente de 0.135. Esto es, la acumulación de los factores de la producción, en el corto plazo, definen en mayor medida el crecimiento económico en correspondencia con los modelos de crecimiento exógeno.
Respecto al cambio tecnológico, para el corto plazo se tiene que ante cambios unitarios porcentuales en esta variable la PTF aumenta en 0.74 %. Este coeficiente es semejante al de largo plazo, no obstante, para el corto plazo ocuparía la tercera posición en orden de importancia.
Por último, la evidencia del mecanismo de corrección de error (O) muestra la velocidad con la cual el modelo converge al equilibrio en el largo plazo. Se cumple, además, con las especificaciones del modelo, es decir, es negativo, inferior a la unidad y significativo (Blackburne y Frank, 2007; Pesaran et al., 1999). La interpretación de (O) muestra que ante choques o alteraciones de las variables seleccionadas el modelo se corrige en un 0.182, es decir, en un 18 % de forma anual. De esta manera, la velocidad de ajuste del modelo se alcanza en 5.5 años,3 lo que reflejaría la dinámica de ajuste del corto al largo plazo.
Conclusiones
En este trabajo se revisan los factores que inciden en el crecimiento de la PTF a partir de la función de producción Cobb-Douglas en catorce economías de América Latina -Argentina, Bolivia, Brasil, Chile, Colombia, Costa Rica, Ecuador, Guatemala, Jamaica, México, Paraguay, Perú, Uruguay y Venezuela, durante el periodo 1990-2019.
La metodología instrumentada es la estimación para datos panel del “Grupo de Medias Agrupadas” (PMG), con la finalidad de capturar el comportamiento de los factores de la producción trabajo y capital, así como el cambio tecnológico sobre la PTF. Se consideran en este proceso las pruebas de dependencia transversal, raíz unitaria y cointegración.
Se realizaron pruebas previas al proceso de estimación del modelo de datos panel, evidenciando que existe dependencia transversal de las variables en las economías seleccionadas, el comportamiento de las series es estacionario con grado de integración I(1) y las variables en el largo plazo se encuentran cointegradas. En el proceso de estimación se aplica la propuesta de Pesaran et al. (1999) PMG, que combina los paneles de datos dinámicos y los estimadores de medias grupales.
De lo resultados de la estimación del modelo PMG se encontró evidencia de que en el corto y en el largo plazo las variables trabajo, capital y cambio tecnológico tienen una relación directa con la PTF. En los coeficientes del trabajo se encontró que en el largo plazo ante un cambio del 1 % en esta variable la PTF se incrementaría en un 0.0871 %; mientras que, en el corto plazo el aumento en la PTF sería del orden del 0.580 %.
En el largo plazo las variaciones del factor capital en 1 % originan que la PTF aumente en 0.018 %; en tanto que, en el corto plazo se tiene un mayor aumento, siendo este del 0.135 %. Por lo que se refiere al cambio tecnológico, en el largo plazo un cambio del 1 % da lugar a un incremento de la PTF del 0.073 %; en el corto plazo, los efectos de esta variable sobre la PTF son similares a los que se tienen en el largo plazo (0.074 %).
En el largo y en el corto plazo el orden de importancia de los efectos de las variables explicativas sobre la PTF presenta cambios significativos. El factor trabajo antes que el capital y cambio tecnológico es el que más incide sobre la PTF, mientras que, el capital en el corto plazo ocupa el segundo lugar y en el largo plazo tiene la tercera posición; por lo que respecta al cambio tecnológico en el corto plazo tiene el tercer orden de importancia y en el largo plazo se sitúa en la segunda posición. Esto es, se corrobora el planteamiento de la teoría económica neoclásica de los modelos de crecimiento exógeno propuestos primeramente por Solow (1956), los cuales establecen que, en el largo plazo no será la acumulación de factores físicos la que conduzca al crecimiento económico, sino el avance tecnológico.
Se confirma la hipótesis establecida en este artículo según la cual el capital (K), el trabajo (L), y el cambio tecnológico (A) fueron los determinantes de la PTF en las economías de América Latina durante el periodo 1990-2019.
Dentro de las futuras líneas de investigación se encuentran: a) considerar estudios a nivel subregional en América Latina con la finalidad de identificar condiciones económicas similares entre los países y así, revisar la incidencia de las variables independientes de esta investigación en la PTF de estos espacios geográficos; b) realizar el estudio a nivel sectorial, para revisar de manera comparativa la influencia de los factores de la producción y el cambio tecnológico en la PTF de las economías latinoamericanas; y, c) incorporar dentro de las principales directrices de este trabajo las variables ambientales, dada la importancia que ha venido adquiriendo la PTF verde (GTFP, por sus siglas en inglés), como un indicador enfocado a la sostenibilidad ambiental.
