Introducción
El uso de fuentes de energías renovables para la producción de energía eléctrica se ha incrementado constantemente en los últimos años, debido a políticas públicas de algunos países para reducir la contaminación ambiental producto del uso de fuentes de combustibles fósiles, pero también para llevar la energía eléctrica a lugares remotos donde la red eléctrica tradicional no llega. De acuerdo con el reporte del estatus global de las energías renovables del 2022, durante el año 2011 el 20.4 % de la energía eléctrica provenía de fuentes renovables, principalmente hidráulica, solar, eólica, bioenergía, y geotérmica. Para el 2021, este porcentaje pasó a 28.3 % (15 % hidráulica, 10 % solar y eólica, 3 % bioenergía y geotérmica). En cuanto a la energía solar fotovoltaica, para el 2021 hubo 942 GW de capacidad instalada para generación de energía eléctrica a nivel mundial, un incremento del 23 % con respecto al 2020 [1].
El uso de la energía solar para la producción de energía eléctrica ha tenido una evolución tecnológica importante, de modo que el uso de plantas solares fotovoltaicas conectadas a la red eléctrica externa ha ido en aumento, incrementándose 20 % a nivel mundial para el 2021 [1]. Ahora bien, la energía proveniente de plantas solares fotovoltaicas está sujeta a las variaciones climáticas, específicamente de la irradiancia solar y la temperatura, por lo que, para coadyuvar en la estabilidad y confiabilidad del sistema eléctrico, se requiere el desarrollo de pronósticos de esa energía generada considerando los datos históricos de esas variables climáticas. Adicionalmente, este pronóstico también sería de ayuda para la gestión de la operación y el mantenimiento de estas plantas solares fotovoltaicas.
Por lo anterior, el objetivo de esta investigación es presentar una metodología basada en la ciencia de datos para desarrollar el pronóstico de la generación de energía eléctrica de plantas solares fotovoltaicas, y adicionalmente, presentar un estudio comparativo de tres técnicas diferentes para obtener los modelos de pronósticos: modelo ARIMA (Autoregressive Integrated Moving Average) del análisis de series de tiempo, regresión lineal múltiple, y red neuronal artificial. Para la evaluación de los modelos se utilizan las métricas: error absoluto medio (MAE), la raíz cuadrada del error cuadrático medio (RMSE), el error porcentual absoluto medio (MAPE), y el coeficiente de determinación R 2 .
Debido a lo anterior, se hizo una revisión de distintas investigaciones relacionadas con los objetivos aquí propuestos, y se encontró una variedad de publicaciones al respecto. Por ejemplo, Mittal et al. [2] hacen una revisión del uso del aprendizaje automático para pronosticar la energía fotovoltaica, reafirmando que la irradiancia solar y la temperatura son importantes para este pronóstico. Concluyen que, para una mejor predicción de la energía solar fotovoltaica, los modelos híbridos son los de mejor desempeño.
Sharkawy et al. [3] desarrollan un estudio en el cual utilizan una red neuronal para crear un modelo de pronóstico de potencia de una planta solar en el muy corto plazo. Para ello toman cinco días de datos para entrenar el modelo, y el día restante de datos para evaluar dicho modelo. Las variables de entrada son la temperatura y la radiación. Concluyen que el modelo obtenido es adecuado, puesto que en el entrenamiento tuvo un RMSE de 0.187 MWh, y en la fase de pronóstico el error absoluto fue de 0.08 MWh. Por otra parte, Kasagani y Manickam [4] realizan un estudio de pronóstico diario de la energía eléctrica haciendo uso de redes neuronales artificiales, y los datos históricos de la planta solar fotovoltaica, de potencia, horas de operación, radiación solar global diaria y temperatura ambiente. Como métrica de desempeño utilizan el RMSE relativo. Encuentran que el pronóstico usando una red neuronal artificial con tres neuronas en la capa oculta tuvo el mejor desempeño, con un MAPE de 4.18 %, y un RMSE relativo de 5.74 %. Pattanaik et al. [5] efectúan un análisis comparativo de distintos métodos para el pronóstico de potencia de una planta solar fotovoltaica. Encuentran que el pronóstico usando algoritmos genéticos es mucho más conveniente y preciso en comparación con el método estadístico de análisis.
Akhter et al. [6] hacen una revisión de los métodos de pronóstico de energía eléctrica generada por plantas solares fotovoltaicas, basados en aprendizaje automático y técnicas metaheurísticas. Presentan las ventajas y desventajas de cada método, y desarrollan una comparación entre los métodos heurísticos y los de aprendizaje automático. Concluyen que las técnicas híbridas (compuestas por al menos dos métodos), presentan la mejor exactitud, para todos los horizontes de pronóstico, con una reducción de alrededor del 15 % en el MAPE y en el RMSE. Asimismo, Alaraj et al. [7] desarrollan un modelo basado en ensamblaje de árboles de decisión para el pronóstico de potencia de una planta solar fotovoltaica, utilizando datos meteorológicos de la ciudad de Qassim en Arabia Saudí, y comparan sus resultados con otros modelos. Para evaluar el modelo, toman en cuenta las métricas RMSE, MAE, MAPE, y el tiempo de entrenamiento. Concluyen que el modelo ENBG es el que presenta el mejor desempeño, con un MAE de 8.89 W en la fase de entrenamiento, y 12.05 W en la fase de prueba.
Anuradha et al. [8] realizan el análisis de pronóstico de potencia de una planta solar fotovoltaica aplicando distintas técnicas de aprendizaje automático, y utilizando datos históricos de variables climáticas más los de la potencia generada. Las técnicas utilizadas fueron máquina de soporte vectorial, bosques aleatorios, y regresión lineal. Concluyen que el modelo de regresión de bosques aleatorios fue el que tuvo mejor exactitud en sus resultados, con un 94.01 %. Finalmente, Borunda et al. [9] presentan una metodología rápida para evaluar la mejor ubicación de una planta solar fotovoltaica, así como para pronosticar la energía eléctrica que generará, utilizando datos históricos de variables climáticas y algoritmos de aprendizaje automático. Validan la metodología comparándola con plantas solares fotovoltaicas reales, a lo largo de México.
El resto del artículo se distribuye de la siguiente manera. En la sección 2 se explica la metodología utilizada y se presentan los datos utilizados en la investigación. Seguidamente, en la sección 3 se discuten los resultados obtenidos. Luego se presentan las conclusiones que se derivan de la investigación, y al final se presenta un listado con las referencias bibliográficas utilizadas.
Materiales y métodos
La metodología de trabajo utilizada consiste en aplicar las etapas de un proyecto de ciencia de datos, y dentro de cada una de esas etapas, aplicar su propia metodología. Según VanderPlas [10], la ciencia de datos es un área interdisciplinaria que solapa a su vez a tres áreas distintas: las habilidades estadísticas para modelar y resumir datos, las habilidades informáticas para diseñar y utilizar algoritmos que permitan almacenar, procesar, y visualizar estos datos de manera eficiente, y la experiencia en el campo o negocio específico de la investigación. En este trabajo, este campo sería el de la generación de energía eléctrica a partir de plantas solares fotovoltaicas.
En el trabajo desarrollado en Cielen [11] se presentan las etapas de un proyecto de ciencia de datos. La primera de ellas corresponde al establecimiento de los objetivos a alcanzar, lo que requiere de un conocimiento del campo, es decir, de la generación a partir de plantas solares fotovoltaicas, y de las necesidades que se quieren satisfacer. La siguiente etapa consiste en obtener o extraer los datos de interés, y para este caso corresponden a las mediciones regulares de las variables en una planta solar fotovoltaica, a partir de su sistema de adquisición de datos. Las variables requeridas para conformar el conjunto de datos van a depender del o de los objetivos del proyecto. Una vez se tiene disponible el conjunto de datos, la siguiente etapa es la del procesamiento de estos, lo que consiste en revisar, limpiar, transformar, y/o combinar estos datos para que tengan la estructura adecuada. Posteriormente, se lleva a cabo un análisis exploratorio de los datos, utilizando técnicas estadísticas, y técnicas gráficas, que pudieran ser univariadas, bivariadas, o multivariadas. En esta etapa es posible ya encontrar conocimiento de interés para el campo de estudio, por esta razón algunos proyectos llegan hasta esta etapa. Pero, si los conocimientos de la etapa anterior no son suficientes, o si la idea es seguir adelante, se tiene la etapa de modelación de los datos, la cual consiste en aplicar algoritmos matemáticos para obtener modelos que nos brinden una mayor profundidad en el conocimiento adquirido. La cantidad y tipo de algoritmos a aplicar depende de los objetivos planteados en la primera etapa. Finalmente, con los resultados obtenidos, se procede a la etapa de toma de decisiones.
Pudiera parecer que las etapas de un proyecto de ciencia de datos se aplican de manera secuencial, pero pudieran existir casos en los que no sea de esa manera. Es decir, dependiendo de los resultados obtenidos en la etapa de análisis exploratorio y/o en la etapa de modelación, podría ser necesario regresar a la etapa de procesamiento de los datos para mejorar su estructura, a la etapa de obtención de los datos para obtener alguna otra variable, o incluso a la primera etapa para reformular los objetivos del proyecto.
Para efectos de ilustrar la metodología, esta se aplica a los datos de una planta solar fotovoltaica en particular, para lo cual, en esta sección se presenta la etapa de obtención de los datos, y la etapa del procesamiento de estos. Mientras que, en la siguiente sección se presentan las etapas del análisis exploratorio de los datos, y la de modelación de los datos.
Obtención de los datos
Los datos utilizados en esta investigación provienen del sistema de adquisición de datos de una planta solar fotovoltaica perteneciente al laboratorio nacional de energías renovables de los Estados Unidos (NREL por sus siglas en inglés), ubicada en Golden, Colorado. Se extrajeron de la página web del set de datos públicos del sistema de adquisición de datos del NREL [12].
La planta está compuesta de cinco paneles solares de mono silicio, marca Sanyo, de 200 vatios de potencia pico cada uno [13]. Están instalados en un montaje fijo, con 40° de inclinación, y ángulo azimut de 180°. Los datos corresponden a mediciones realizadas y almacenadas cada minuto, de potencia pico de salida de la planta (“ac_power”), en vatios, temperatura ambiente (“ambient_temp”) en grados Celsius, irradiancia (“poa_irradiance”) en vatios por metro cuadrado, velocidad del viento en metros por segundo (“wind_speed”), y tasa de suciedad (“soiling”). Los datos inician el 25 de febrero del 2010 y culminan el 13 de diciembre del 2016, para un total de 1 558 875 filas (registros o instancias).
Procesamiento de los datos
En esta etapa, se aplican las técnicas de procesamiento de datos, entre las que se encuentran: detección de posibles datos faltantes o filas duplicadas, detección de datos atípicos, transformación de datos, combinación de columnas de datos, y verificación del formato adecuado para las distintas variables. Estas y otras técnicas se encuentran en [14], junto con la manera de aplicarlas utilizando el lenguaje de programación Python.
Luego de una revisión inicial, se detectan siete datos faltantes en la variable de temperatura ambiente, y 17 362 datos faltantes en la variable de velocidad del viento. Las filas con datos faltantes de temperatura corresponden a menos del 0.001 % de las filas totales, mientras que las filas de velocidad del viento con datos faltantes corresponden a aproximadamente el 1.11 % de las totales. A pesar de ser porcentajes bajos, se decidió imputarlos con el valor medio de los tres datos más cercanos al dato faltante. Por otra parte, no se detectaron filas duplicadas.
Además de eso, a partir de los datos de la columna original de la fecha, se crean columnas correspondientes al año, mes, semana, día y hora de la lectura de datos. Así mismo, a partir de la columna de potencia eléctrica pico, se crea la columna de energía eléctrica generada (“ac_energy”) en kilovatios hora (kWh), la que es utilizada como la variable objetivo en los modelos de pronóstico. En cuanto a la temperatura ambiente, esta fue cambiada de escala, pasando de unidades de grados Celsius a unidades Kelvin.
Por otra parte, se detectó que para el año 2010 no existían registros para los meses de enero, septiembre y octubre, lo que podría perturbar los resultados del análisis exploratorio. En consecuencia, este análisis se realiza con los datos existentes entre los años 2011 y 2016.
Análisis y resultados
En esta sección se presentan las etapas de análisis exploratorio, y modelación de los datos, con la respectiva discusión de resultados.
Análisis exploratorio de los datos
Después del procesamiento a los datos realizado en la etapa anterior, se tiene un total de 1 429 678 filas o registros correspondientes a los valores minutales de las mediciones de las variables, así como de las otras variables que se generaron. Para efectos del análisis se obtuvieron set de datos con resoluciones diaria, semanal, mensual y anual. Esto se logró agrupando los datos originales con resolución minutal, en el período de tiempo correspondiente.
En primer lugar, se obtuvo un análisis descriptivo de los datos diarios, utilizando estadísticos univariados. Los resultados se presentan en la Tabla 1. Se puede observar que a excepción de la tasa de suciedad (soiling), las variables tienen su valor medio cercano al valor de la mediana. Así mismo, se puede ver que el rango de las variables: irradiancia solar y velocidad del viento es alto, con su valor medio más cercano a su valor mínimo que a su valor máximo.
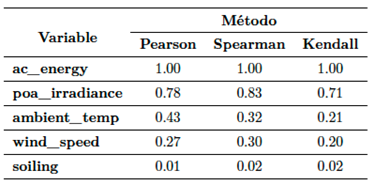
Seguidamente, se hizo un análisis de correlación considerando a las variables climáticas, la tasa de suciedad, y la generación eléctrica AC, con datos en la escala diaria. De acuerdo con Navlani et al. [15], para el cálculo del coeficiente de correlación, el método de Pearson aplica cuando los datos se distribuyen de manera simétrica (normales), pero cuando en los datos hay asimetría y/o datos atípicos, se prefiere el uso del método de Spearman. El método de Kendall también se usa cuando no se requiere que los datos sigan algún tipo de distribución. Por lo anterior, y para efectos de comparación, se utilizan los tres métodos para el cálculo de los coeficientes de todas las variables con respecto a la energía eléctrica AC. Los resultados obtenidos se presentan en la Tabla 2.
Para la interpretación de los valores de la Tabla 2 se debe recordar que el coeficiente de correlación varía entre “-1” y “1”. Cuando el valor es positivo, significa que el sentido de crecimiento o de decrecimiento del par de variables es el mismo, y si el valor es negativo, el sentido es inverso. Por otra parte, el valor absoluto “1” significa que la magnitud de crecimiento o decrecimiento es igual para ambas variables, mientras que un valor “0” significa que el par de variables no están relacionadas en lo absoluto. Para los valores entre “0” y “1” se toma en cuenta lo planteado por Ratner [16] quien postula que “valores entre 0 y 0.3 (0 y -0.3) indican una relación positiva (negativa) débil. Los valores entre 0.3 y 0.7 (-0.3 y -0.7) indican una relación positiva (negativa) moderada. Los valores entre 0.7 y 1.0 (-0.7 y -1.0) indican una fuerte relación positiva (negativa)”.
De la Tabla 2 se puede ver entonces que la irradiancia solar tiene una relación fuerte y positiva con la energía eléctrica. Se podría decir también que la temperatura ambiente tiene una relación positiva y moderada con la energía eléctrica. La relación de la velocidad del viento con la energía eléctrica es positiva, y entre débil y moderada. Mientras que, para este caso, la relación entre la tasa de suciedad y la energía eléctrica es prácticamente de independencia.
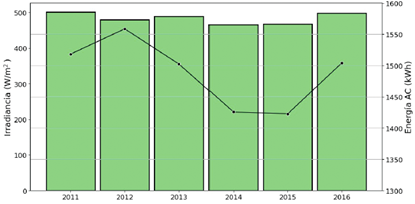
Por otra parte, a continuación, se generan curvas temporales de las principales variables del conjunto de datos. En ese sentido, en la Figura 1 se presenta como ha sido la irradiancia solar promedio (barras) versus la energía eléctrica generada (línea) para cada uno de los años del período de estudio.
Se puede observar que la irradiancia solar promedio se ha mantenido aproximadamente constante durante el período de estudio, mientras que la energía generada tuvo su máximo en el 2012, luego disminuyó hasta tener valores mínimos durante 2014 y 2015, y aumentó nuevamente durante el 2016.
Además, en la Figura 2 se presentan los valores mensuales promedio de la irradiancia solar y la potencia eléctrica, así como también la energía AC generada en el respectivo mes. Se puede ver que la producción mensual de energía se ha mantenido relativamente constante durante todo el período, y se observa que el comportamiento de la potencia sigue casi perfectamente al comportamiento de la irradiancia solar.
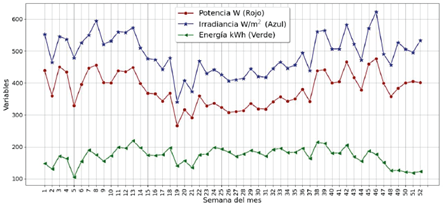
Asimismo, en la Figura 3 se presentan los valores promedios semanales de la irradiancia solar y la potencia eléctrica, así como también la energía generada AC por semana del año. Se puede ver que el comportamiento de la potencia eléctrica y la irradiancia solar es casi idéntico. En cuanto a la energía eléctrica, se observa que tiene su valor mínimo para la semana cinco del año, y su máximo en la semana trece. También se puede ver que la energía generada cae en las últimas cinco semanas del año.
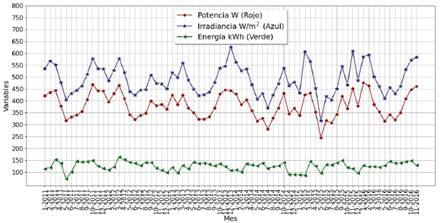
En cuanto a la escala diaria, en la Figura 4 se presentan los valores promedio diarios de la irradiancia solar y la potencia eléctrica, y la energía generada en cada uno de los respectivos días del mes. A diferencia de las curvas anteriores, en este caso se puede ver que las formas de las tres curvas son aproximadamente iguales, con valores mínimos al inicio y a mediados del mes. Asimismo, se puede decir que las curvas no tienen ningún tipo de tendencia definida (ascendente o descendente).
Adicionalmente, para efectos de visualizar la simetría y dispersión de los datos, en la Figura 5 se presentan los diagramas Box-Plot de cada una de las variables en la escala semanal. Previamente, los valores de cada variable fueron llevados a una escala entre cero y uno, para poderlas comparar.
De la Figura 5 se puede decir que, a excepción de la temperatura ambiente, todas las otras variables presentan valores atípicos. Es importante resaltar que son valores atípicos leves, según la prueba de Tukey [17], por lo que no son imputados. De igual forma, se puede ver que la irradiancia solar es la variable más simétrica de todas, además de tener pocos datos atípicos. Asimismo, la tasa de suciedad es la variable con más datos atípicos y mayor asimetría. La temperatura ambiente es la que presenta mayor dispersión en sus datos, y la irradiancia solar es la variable con menor dispersión.
Modelación de los datos
Seguidamente se aplican algoritmos matemáticos para obtener modelos de pronóstico de la energía eléctrica generada. Específicamente se obtiene un modelo de regresión lineal múltiple, un modelo de regresión de red neuronal artificial, y un modelo de análisis de series de tiempo, utilizando los datos semanales. Los datos corresponden a 310 semanas, desde la semana 41 del 2010, hasta la semana 47 del 2016. Los datos de la semana 48 a la semana 50 del 2016, se utilizan para comparar el pronóstico obtenido de los tres modelos mencionados.
Algoritmo de Regresión lineal múltiple
El algoritmo de regresión lineal múltiple (RLM) es un algoritmo de aprendizaje automático del tipo supervisado. El modelo que se obtiene a partir de este algoritmo es lineal en los parámetros (coeficientes) y no necesariamente en las variables explicativas o predictoras. La variable objetivo es la energía eléctrica AC en kWh, mientras que las variables predictoras son irradiancia solar (“poa_irradiance”), la temperatura ambiente (“ambient_temp”), y la velocidad del viento (“wind_speed”). No se consideró a la tasa de suciedad (soiling) debido a su correlación nula con la variable objetivo, y, además, en un primer modelo de regresión su coeficiente en la ecuación de regresión resultó que no era estadísticamente significativo.
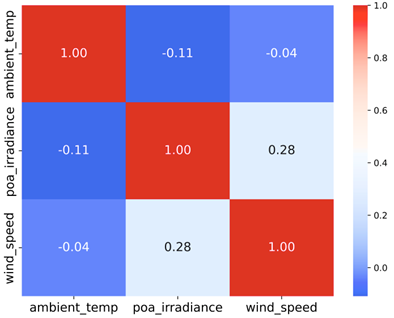
Se verifica que no hay correlaciones significativas entre las variables predictoras, tal como se muestra en la Figura 6, en la que se observa que todos los valores absolutos de coeficiente de correlación son menores a 0,3, indicando que las relaciones son débiles entre las variables.
El conjunto de datos, conformado por la variable objetivo más las variables predictoras, fue dividido, de manera aleatoria, en dos partes. La primera parte compuesta por el 80 % de los datos (256 registros) se utiliza para la creación y entrenamiento del modelo de regresión. La segunda parte, compuesta por el 20 % (64 registros), se utiliza para evaluar el modelo obtenido en la fase de entrenamiento. Las métricas utilizadas para la evaluación del modelo son MAE y RMSE, pues según [18] son medidas estadísticas que se utilizan para evaluar modelos. Asimismo, se utiliza el R 2 , el cual de acuerdo con Black et al. [19] es una “medida de la proporción de la varianza de la variable dependiente con respecto a su media que es explicada por las variables independientes o predictoras”. Alaraj et al. [7], utilizan las mismas métricas, a excepción del R 2 .
Luego de aplicar el algoritmo, se obtuvieron los siguientes coeficientes: 0.446, 0.043 y 4.002, para las variables predictoras temperatura ambiente, irradiancia solar y velocidad del viento, respectivamente. Esto implica que un aumento unitario en el promedio semanal de la temperatura ambiente significa un aumento de 0.446 kWh, un aumento unitario de la irradiancia solar implicaría un aumento de 0.043 kWh en la generación de energía, y un aumento unitario en el promedio semanal de la velocidad del viento significa un aumento en la generación de energía semanal de alrededor de 4 kWh. De igual forma, el valor del intercepto es de -125.98.
En cuanto a las métricas de desempeño, los resultados se presentan en la Tabla 3. Se puede ver que las variables predictoras explican alrededor del 81 % de la varianza de la variable objetivo, es decir, el modelo presenta una buena calidad de ajuste. Por otra parte, dado que la media de la energía eléctrica generada semanalmente es de 29 kWh, el RMSE obtenido (2.87) corresponde a casi el 10 % de la media, y el MAE obtenido (2.30) es casi el 8 % de la media.
Para verificar el supuesto estadístico de normalidad de los residuos que requiere este tipo de modelos, se utiliza el test estadístico de Shapiro-Wilk, que tiene como hipótesis nula que los datos se distribuyen normalmente. El estadístico de prueba varía entre 0 y 1, y cuando está cercano a 1 es un indicativo de que los datos se distribuyen normalmente. Adicionalmente, para verificar el rechazo o no de la hipótesis nula, se cuenta con el p-valor. Entonces, en la Tabla 3 también se observa que el valor de 0.995 para el estadístico, más un p-valor de 0.998 (superior al 5 % de significancia estadística) sugieren que no hay suficiente evidencia para rechazar la hipótesis nula de que los residuos se distribuyen normalmente [20].
Algoritmo de red neuronal artificial
Al aplicar la red neuronal artificial (RNA), se utilizaron los mismos datos que para el modelo de regresión lineal múltiple, al igual que la misma variable objetivo, y las mismas variables predictoras. Así mismo, para la validación cruzada del modelo también se utilizó el 80 % de los datos (256 registros) para su entrenamiento, y 20 % de los datos (64 registros) para su evaluación.
De acuerdo con Kapoor et al. [21] se trabaja con un modelo llamado “perceptrón multicapa”, el cual está compuesto por la capa de entrada, la capa de salida, y un grupo de capas ocultas ubicadas entre la entrada y la salida. Para este estudio se utilizan tres capas: una de entrada, otra de salida y una oculta. Todas las capas son densas, pues según lo que plantea Moolayil [22] “una capa densa es una capa regular que conecta todas sus neuronas con todas las neuronas de la capa previa”.
Por otra parte, se definen funciones de activación para cada una de las capas de la red. Para las capas de entrada y oculta se aplica la función de activación lineal rectificada (ReLU), la cual permite el paso de solo valores positivos. Estas dos capas tienen un total de 256 neuronas cada una. En cuanto a la capa de salida, esta tiene una función de activación de tipo lineal con el fin de no limitar los valores del pronóstico, y solo tiene una neurona, pues es lo que se necesita para pronosticar la energía eléctrica. Según Chollet [23], adicionalmente se requiere una función de pérdida, la cual se utiliza para controlar la desviación del pronóstico con respecto a su valor esperado, de manera que para este estudio se utilizan el MAE y el MSE como funciones de pérdida. Si la desviación no es adecuada, se realimenta su valor hacia la entrada a través de una función de optimización, la que. según Chollet [23], actualiza los pesos de las entradas y se repite el ciclo. En esta investigación se hace uso del optimizador de propagación de raíz cuadrática media (RMSProp). Sharkawy et al. [3] también utilizan una RNA, con tres capas, pero con función de activación hiperbólica.
Los resultados obtenidos al aplicar el algoritmo RNA se presentan en la Tabla 4. Se puede ver que la calidad del ajuste es alrededor del 88 %, el cual es mejor al obtenido con el modelo RLM. De igual manera, se puede notar que tanto el RMSE como el MAE obtenidos son menores a los obtenidos con el modelo RLM. En cuanto al análisis de los residuos, se puede observar que se distribuyen normalmente, pues el estadístico de prueba es cercano a uno, y el p-valor es mayor al 5 % de significancia estadística.
Análisis de series de tiempo
Al aplicar el análisis a la serie de tiempo de la energía eléctrica AC generada, se obtiene un modelo ARIMA, el cual requiere de tres parámetros, el orden de la parte autoregresiva p, el orden de integración d, y el orden del promedio móvil q. Además de esto, si la serie resulta estacional, también deben considerarse los tres parámetros para la parte estacional (P, D, Q). El modelo se obtiene aplicando la metodología Box-Jenkins, la cual se presenta en [24], y es mencionada con mayor detalle en [25].
La metodología inicia con la preparación de los datos, lo que pudiera incluir su transformación para estabilizar la varianza y/o su diferenciación para hacer la serie estacionaria (se define el parámetro d). Luego se seleccionan modelos iniciales potenciales, haciendo uso de la función de autocorrelación y de la función de autocorrelación parcial (se definen los parámetros p y q). Se estiman los parámetros de los modelos potenciales, y se selecciona el mejor de ellos utilizando un criterio de desempeño, que por lo general es el AIC (Akaike Information Criteria), el que según [26] es quizás el más popular para la selección del mejor modelo. Posteriormente, se pasa a la etapa de diagnóstico, en la que se desarrolla un análisis de los residuos, para verificar que sean iguales o aproximadamente iguales a un ruido blanco. Finalmente, se utiliza el modelo para realizar el pronóstico de la serie de tiempo.
Siguiendo la metodología, se aplica el test de Dickey-Fuller ampliado para verificar la estacionariedad de la serie de energía AC. De acuerdo con Gujarati y Porter [27], esta prueba también se conoce como prueba de la raíz unitaria, y es popular en la determinación de la estacionariedad o no de una serie de tiempo. El estadístico de prueba resultó menor a los tres valores críticos (1 %, 5 %, 10 %), y, además, el p-valor es aproximadamente igual a cero, por lo que se rechaza la hipótesis nula de existencia de raíz unitaria, y por consiguiente se puede decir que la serie en nivel es estacionaria. Esto último implica que el parámetro d vale cero.
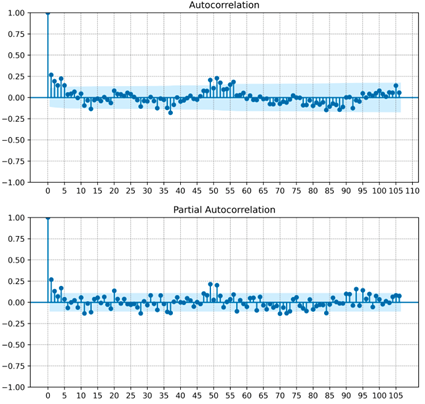
Posteriormente, en la Figura 7 se muestran los gráficos de la función de autocorrelación (superior) y la función de autocorrelación parcial (inferior) de la serie de energía AC, considerando hasta 106 rezagos, puesto que los datos presentan estacionalidad anual (52 semanas). Se puede ver que hay por lo menos dos valores de autocorrelación significativos, y se confirma que la serie es estacional, con el primer valor estacional (semana 52) significativo para ambos gráficos, lo cual debe considerarse en el modelo que se proponga.
Luego de realizar las iteraciones correspondientes, minimizando el valor de la métrica AIC y chequeando las características de los residuos obtenidos con cada uno de los modelos, el modelo seleccionado para hacer los pronósticos es: ARIMA(0,0,2)(1,1,1)52. A continuación, se presentan los resultados obtenidos del pronóstico realizado con el modelo ARIMA, así como por los otros modelos.
Comparación de los pronósticos
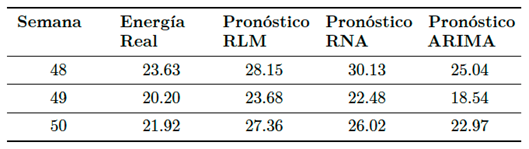
Como se mencionó previamente, se realiza el pronóstico de la energía eléctrica generada para las semanas 48, 49 y 50 del año 2016, utilizando cada uno de los tres modelos. Se evalúan utilizando las métricas RMSE, MAE, y MAPE. Los resultados del pronóstico de energía en kWh se presentan en la Tabla 5, de la cual se observa que el pronóstico del modelo ARIMA es el que está más cercano a los valores reales de energía generada.
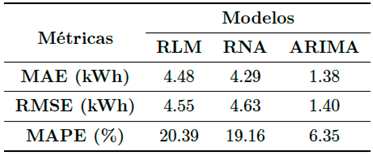
Por otra parte, en la Tabla 6 se presentan las métricas de desempeño de los tres modelos para los pronósticos presentados en la Tabla 5. Se confirma que el modelo ARIMA es el que presenta mejor desempeño con un MAPE de alrededor del 6 % contra casi 20 % para los otros dos modelos. De igual forma, se puede ver que el MAE y el RSME son mucho menores en el caso del modelo ARIMA.
Los resultados que se presentan en la Tabla 6 concuerdan con lo indicado por [25] pues estos autores proponen que los métodos de promedios móviles son convenientes para el corto plazo, mientras que los métodos de regresión son más adecuados para el mediano y largo plazo. Para estos autores el “corto plazo” está asociado a períodos de hasta tres meses de duración, mientras que el “largo plazo” son períodos de más de dos años.
Conclusiones
El comportamiento en el tiempo de la energía eléctrica generada es similar al comportamiento de la irradiancia solar para los datos con resolución cercana a la resolución minutal de las mediciones, es decir, resolución diaria. Este resultado concuerda con el análisis de correlación, del cual se obtuvo que la irradiancia solar tiene un valor de correlación de 0.78 con la energía eléctrica generada. Con respecto a la temperatura ambiente y la velocidad del viento, el coeficiente de correlación con la energía eléctrica está entre moderado y débil, con 0.43 y 0.27, respectivamente.
Las variables predictoras del modelo de regresión lineal múltiple explican el 81 % de la variabilidad de la variable objetivo, y del análisis de los residuos derivados de este modelo, se desprende que estos siguen una distribución normal. En cuanto al modelo de red neuronal artificial, el coeficiente de determinación resultó en un 88 %, los indicadores MAE y RMSE resultaron menores en comparación con el modelo de regresión, y los residuos están normalmente distribuidos.
En el proceso de encontrar el modelo ARIMA adecuado, se determinó que la serie de nivel de energía eléctrica AC es estacionaria, y que, además, tiene estacionalidad anual. El modelo obtenido minimiza el criterio AIC; los residuos se distribuyen de manera independiente, es decir, no están correlacionados serialmente.
Al realizar pronósticos con los modelos obtenidos, el modelo ARIMA resultó con el mejor desempeño, pues arrojó los valores mínimos de los tres indicadores de error: MAE, RMSE, y MAPE, con 1.38 kWh, 1.40 kWh, y 6.35 %, respectivamente. Luego estuvo el modelo de red neuronal con los indicadores MAPE y MAE menores a los obtenidos con el modelo de regresión lineal múltiple, pero con la métrica RMSE más alta de los tres modelos.