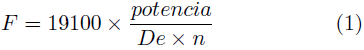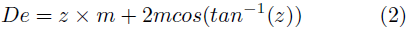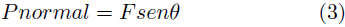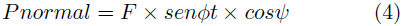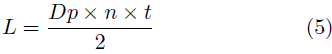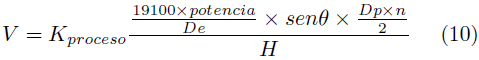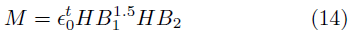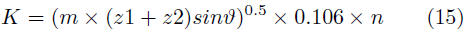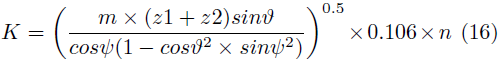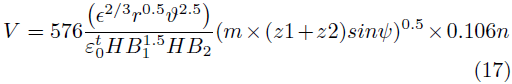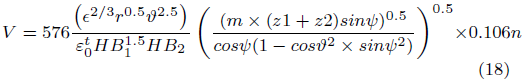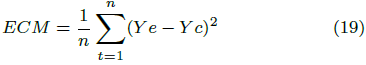Forma sugerida de citación:
Mena Chavarrea, J. M.; Granizo, J.A.; Hernández Dávila, E.S. y Audelo Guevara, M.E. “Cálculo de la velocidad de desgaste abrasivo en engranajes de dientes rectos y helicoidales con perfil evolvente, utilizando una GUI de Matlab,” Ingenius, Revista de Ciencia y Tecnología, N.° 29, pp. 32-45, 2023. DOI: https://doi.org/10.17163/ings.n29.2023.03
1. Introducción
Actualmente, los engranajes, como elementos principales de transmisión en sistemas mecánicos, poseen una gran importancia, ya que son piezas mecánicas que se encuentran en toda industria como elemento principal de maquinaria que genera fuerza y movimiento.
El grado de desgaste de los engranajes depende del trabajo realizado por el equipo, el tamaño de grano del abrasivo, la constitución del abrasivo, la potencia con la que trabaja, la carga que se encuentre diseñada, la eficiencia del proceso, la fiabilidad y confiabilidad del proceso. Estos son factores primordiales que se manejan para establecer los costos para la ejecución de mantenimiento correctivo como preventivo.
La detección de fallas de manera oportuna y eficiente constituye uno de los retos más importantes asociados al mantenimiento predictivo. Las fallas imprevistas pueden afectar la integridad y la confiabilidad de los equipos a través de paradas no programadas, reducción de su vida útil, altos costos de asociados al mantenimiento correctivo y baja calidad de los productos [1].
La importancia del estudio del proceso de desgaste de los engranajes va en aumento por ser los elementos de transmisión mecánica de mayor utilización en los diversos campos y condiciones de trabajo, desde engranajes diminutos utilizados en relojes hasta ser una parte que conforma toda una máquina independientemente de su dimensionado.
En la industria, el desgaste es uno de los problemas frecuentes que se producen en los sistemas que contienen engranajes, sin tomar en cuenta el trabajo que se encuentren realizando. Los abrasivos son elementos que se encuentran en el medioambiente y son característicos en elementos de maquinaria pesada, tales como equipo caminero, maquinaria agrícola, maquinaria de la construcción, maquinaria de la industria minera, etc. Las partículas abrasivas son un factor determinante para que la vida útil del engranaje se reduzca de forma significativa.
Los aspectos más importantes a tener en cuenta en el diseño de los perfiles de los dientes de engranajes, están relacionados con la capacidad de carga, diseño de perfil de los dientes, error de transmisión, ángulo de presión, el desgaste y el análisis de fallos [2].
El no aporte y revisión de los criterios de análisis para los diseñadores y encargados de mantenimiento de maquinaria, cuyo motor principal de diseño sean engranajes rectos o helicoidales de perfil evolvente que se encuentre en presencia constante de elementos abrasivos, ha generado que sufran daños en los mecanismos, paras innecesarias hasta la no implementación de procesos de investigación de laboratorio que son extremadamente tardados y costosos.
El abrasivo que se encuentra en los ambientes afecta directamente el rendimiento de los sistemas mecánicos, ya que genera fallas catastróficas que producen pérdidas a los procesos industriales de las empresas. Los parámetros que intervienen son el tamaño del grano, la dureza del abrasivo, la cantidad del abrasivo y del trabajo realizado, que reducen el rendimiento de los procesos industriales y la producción.
Por lo que es necesario estudiarlos de una manera que logre solventar problemas latentes en los engranajes. Es así que el desgaste, el abrasivo y las fallas son aspectos relacionados que serán el caso de estudio para determinar la velocidad de desgaste dependiendo el abrasivo y el material del engranaje. La sustitución de ruedas dentadas en 90 % se debe a la pérdida de la eficiencia de las mismas, producto del desgaste de los dientes; para combatir este fenómeno por lo regular se utilizan los siguientes mecanismos:
Optimización de los parámetros geométricos a partir del diseño.
Mejora de la calidad de la superficie de los dientes y el engrane de sus partes.
Selección adecuada del material y los parámetros de tratamiento térmico.
Selección adecuada del lubricante y optimización del proceso de lubricación [3].
De aquí, se deduce que en la zona del polo de engranaje existirá la mayor posibilidad de formación de una película hidrodinámica, en el caso de que el proceso tribológico sea con presencia de lubricante, entonces en esta zona ocurrirá el menor desgaste en las transmisiones dentadas.
En el presente trabajo se propone la utilización de una interfaz gráfica de usuario con la finalidad de realizar un cálculo teórico de la velocidad de desgaste en engranajes que presentan dientes con perfil evolvente para proveer al diseñador de los sistemas herramientas que permitan predecir el comportamiento del sistema tribológico, evaluar la validez de sus teorías de diseño y generar planes de mantenimiento oportunos.
Ante las aproximaciones reales que se realizan, se toma en cuenta el proceso que se basa de un esquema basado en vibraciones para actualizar un modelo de predicción de desgaste. Se desarrolla en primer lugar un modelo dinámico de un sistema de engranajes rectos para generar vibraciones realistas, lo que permite un estudio cuantitativo de los efectos del desgaste de la superficie de los dientes del engranaje. La velocidad de deslizamiento y las fuerzas de contacto del modelo se utilizan en combinación con el conocido modelo de desgaste de Archard para calcular la profundidad de desgaste en cada punto de contacto en la malla. Dado que el coeficiente de desgaste en el modelo no es constante durante el proceso de desgaste (y en cualquier caso es difícil de estimar inicialmente), las vibraciones medidas se comparan con las generadas por el modelo, para actualizar el coeficiente cuando se detecta una desviación de las predicciones [4].
1.1.Tribología
El término tribología proviene de los vocablos griegos «tribos» con significado fricción y «logos» estudio. Por lo cual este término se utiliza para denominar a la ciencia que estudia las superficies con movimientos relativos entre sí.
Es por ello por lo que terminologías como la fricción, el desgaste de las diferentes superficies y la presencia o ausencia de lubricante entre las partes en contacto es algo indispensable para lograr obtener máquinas y procesos con menor pérdida de energía, evitar excesivos tiempos de para que limiten la eficiencia de la actividad productiva, mejorar los tiempos de vida de máquinas y, sobre todo, tener una herramienta confiable para generar buenas prácticas de reparación y mantenimiento [5].
1.2.Contacto mecánico
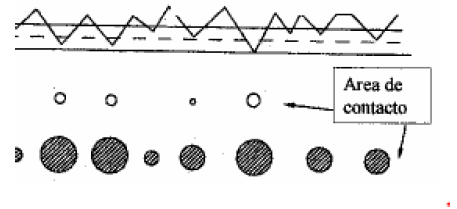
En la Figura 1 se denota que el área aparente, correspondiente a toda la superficie de las piezas en contacto, y el área real, que tiene las consideraciones que las superficies presentan rugosidades que provoca que el contacto ocurra únicamente en algunos puntos donde coinciden las crestas respectivas de cada una de las superficies involucradas en el movimiento [6].
1.3. Desgaste
Es el proceso de destrucción y desprendimiento de material que ocurre entre las superficies de los cuerpos, presentados como acumulación de deformaciones y variación de las dimensiones iniciales del objeto en cuestión [7].
1.3.1. Desgaste abrasivo
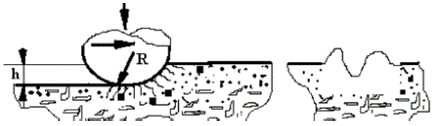
Este mecanismo de desgaste, se caracteriza por la presencia de partículas duras que interactúan con superficies que se deslizan una contra otra. Como se determina en la Figura 2, bajo este sistema es importante caracterizar que este tipo de desgaste provoca imperfecciones, microcortes, entre otros por acción de partículas extremadamente duras y pequeñas, en comparación con la superficie base [8].
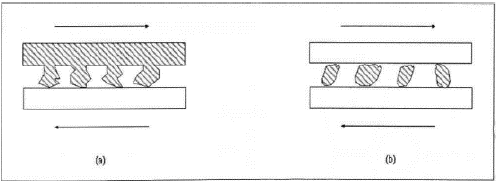
La Figura 3 indica que el desgaste abrasivo se puede clasificar en dos tipos, de acuerdo con la naturaleza pueden ser de dos cuerpos o de tres cuerpos. El desgaste abrasivo de dos cuerpos, generalmente se utiliza como mecanismo de mecanizado, para obtener resultados específicos en una superficie determinada, mientras que el desgaste abrasivo de tres cuerpos es producto de la contaminación de la interfaz entre dos superficies.
1.4. Análisis de fallas en engranajes
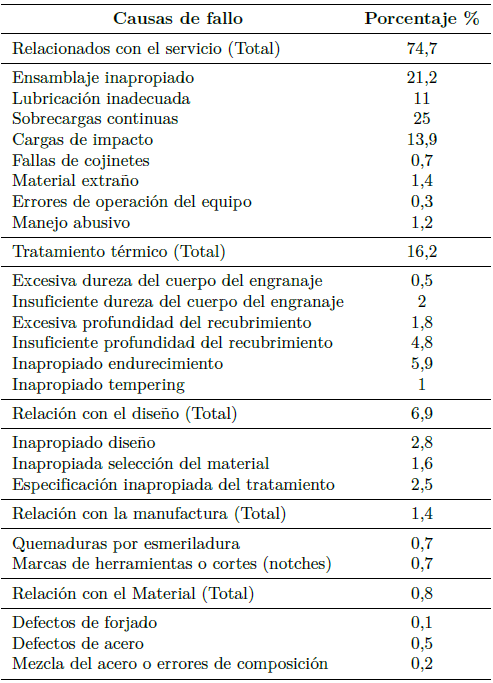
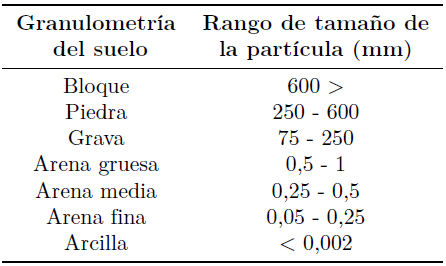
La Sociedad Americana para Metales (American Society for Metals) ha creado cuatro subgrupos para clasificar los modos de falla; desgaste, fatiga superficial, deformaciones y rotura. La Tabla 1 muestra los porcentajes de las fallas comunes que toman en cuenta los parámetros que se establecen a causa del desgaste abrasivo en engranajes, analizando cada modo y consecuencia de falla.
1.5. Matlab
Matlab se presenta como una herramienta de cálculo matemático muy potente y adaptable, con solicitaciones gráficas que mejoran la experiencia de presentación de datos. Estas características han hecho que se vuelva popular como una opción de cálculo en ámbitos de la ciencia e investigación [10].
Una de las características más notables de Matlab es la interfaz de usuario interactiva, que permite el cálculo numérico rápido y un procesamiento de los datos de manera eficiente. Además, tiene varias funciones como la presentación de herramientas gráfica que permiten que la experiencia del usuario sea más sencilla, agradable y lo suficientemente eficiente para poder cumplir todas las necesidades que esté presente sin necesidad de utilizar una infinidad de softwares [11].
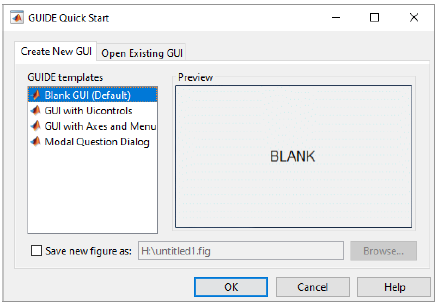
1.5.1. Herramienta GUI
Graphical User Interface, por sus siglas en inglés GUI, es un paquete informático dentro de la aplicación de Matlab que utiliza una serie de imágenes y cuadros de acciones preprogramados para sintetizar las necesidades del usuario de manejo de sus datos y tareas.
La figura 4 determina la función principal de esta herramienta, que es facilitar la comunicación entre el usuario y el software, de manera que no sea necesario considerar los procesos de programación y el lenguaje necesario para modificar y crea la interfaz gráfica [13].
2. Materiales y métodos
La finalidad es obtener las herramientas necesarias teórico-conceptuales, evaluar las fórmulas presentadas en la bibliografía seleccionada, adaptarlas a las circunstancias del problema, ordenar, interpretar y utilizar de manera adecuada los datos obtenidos.
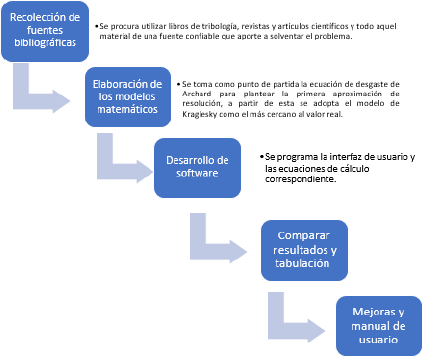
Definir variables dependientes e independientes y según esta información formular un software capaz de calcular la velocidad de desgaste abrasivo de ruedas dentadas mediante una herramienta gráfica de usuario de Matlab, el proceso de seguimiento se determina en la Figura 5.
2.1. Técnicas de recolección de información
Las técnicas utilizadas en el proceso de esta investigación se enfocarán en dos aspectos principales.
2.1.1. Documental-Bibliográfica
Se han recolectado libros, revistas certificadas, artículos científicos y manuales de usuario en torno al desgaste abrasivo de ruedas dentadas y el uso de Matlab. Esta información servirá de base para discretizar y adaptar las ecuaciones de cálculo y modelos matemáticos al problema planteado y nos guiará en el proceso de construcción de la herramienta gráfica de Matlab.
2.1.2. Teórico experimental
Una vez obtenido el software, la validez de las ecuaciones se evaluará en función de los resultados planteados, la similitud entre los modelos matemáticos y las tendencias de la velocidad de desgaste. Al variar los parámetros de las ecuaciones se obtendrá un valor de error y se intentará ajustar las constantes de las ecuaciones para aproximarse de una manera adecuada a valores reales, que permitan tener primeras aproximaciones de diseño. Se toma en cuenta los datos realizados de las aproximaciones reales que se realizan en las pruebas de funcionamiento [4].
2.2. Fundamentos de engranajes
Al considerar la importancia que tienen los engranajes en este trabajo, es importante destacar la función que tienen las herramientas y el conocimiento fundamental para determinar la geometría, tipo, materiales y procesos de fabricación de engranes más comunes que permitan llevar a cabo un proceso correcto de cálculo y dimensionamiento de los mismos.
2.2.1. Terminología
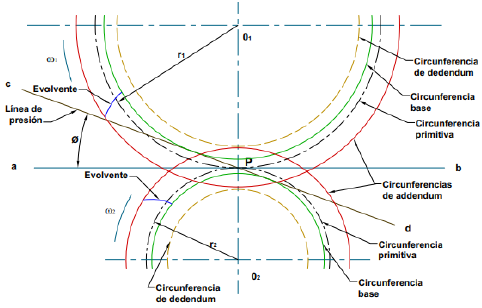
Para introducirse al análisis y estudio de engranajes es necesario la terminología en la Figura 6. Según a la Norma INEN 1143 correspondiente a engranajes, establece:
Dientes de un engranaje. Elementos que realizan el trabajo de empuje, transmiten la potencia y tienen un perfil característico en función de la disposición de los mismos.
Circunferencia exterior. Parte de la circunferencia de la forma del engranaje que limita al mismo por su parte más externa.
Circunferencia interior. Parte que limita el fondo de los dientes, también denominado pie.
Adendum. Distancia perpendicular entre el círculo de paso o circunferencia primitiva y la parte más alta de los dientes.
Ángulo de hélice. Ángulo formado por la base de cilindro y los dientes de un engranaje helicoidal o tipo tornillo de perfil evolvente.
Engranaje o corona. Se refiere al engranaje más grande de un arreglo de engranajes.
Piñón. Engranaje más pequeño, comúnmente encargado de transmitir el movimiento.
Excentricidad. La desviación de los centros comunes de dos circunferencias se denomina excentricidad.
Ancho de cara. La correspondiente longitud del diente en el plano ubicado a 90 grados del plano de formación del engranaje.
Relación de engranaje. Proporción del mayor al menor número de dientes en los engranajes del acoplamiento.
Módulo. Proporción existente entre el diámetro de paso en milímetros como el número de dientes
Paso. Distancia entre un punto del diente a un diente adyacente en el mismo punto. Es una caracterización del tamaño del diente.
Pitch. Superficie plana imaginaria tangente a las superficies de paso de dos engranajes, básicamente, es el plano que limita a los puntos de contacto entre los engranajes.
Ángulo de presión. Ángulo entre la línea de presión del diente y la tangente plana a la superficie de paso. Básicamente, es la dirección normal al diente de un engranaje [15].
2.3. Engranaje recto
Partiendo que la fuerza total en un engranaje viene dada por la Ecuación (1).
Dónde: F es la fuerza total de contacto en engranajes, P la potencia de la máquina en KW, De es el diámetro exterior y n la velocidad angular. El diámetro exterior se determina por la Ecuación (2).
Donde z es el número de dientes y m el módulo del engranaje.
Para el engranaje recto, la fuerza normal aplicada en el proceso viene dada por la Ecuación (3).
Con θ igual al ángulo de presión del engranaje [17].
2.4. Engranaje helicoidal
La fuerza normal aplicada para engranajes helicoidales viene dada por la Ecuación (4).
Donde: ψ = ángulo de hélice y ϕt = ángulo de presión transversal
Para introducir el tiempo como una variable en la fórmula de Archard base de la Ecuación (5) es necesario relacionar la distancia recorrida en el proceso de abrasión con el desplazamiento lineal de la superficie de un engranaje al momento de estar la máquina en funcionamiento.
Con n igual a la velocidad angular, t es la variable de tiempo, y Dp el diámetro primitivo del engranaje, como de la Ecuación (6):
De, es diámetro exterior, y z el número de dientes del engranaje.
2.5.Cálculo del desgaste abrasivo
Según la Ecuación (7) la pérdida volumétrica de volumen (W) de una pieza es directamente proporcional a la probabilidad (z) que una partícula abrasiva remueva material cuando se encuentra en su camino con una cresta de la superficie y a la fuerza normal (N) que actúa entre las superficies deslizantes y las partículas abrasivas e inversamente proporcional a la dureza de las mismas medidas en escala Brinell (HB) [18].
La Ecuación (8) muestra la partícula abrasiva que tiene formas semiesféricas con un radio igual al radio del punto de contacto entre las superficies.
Donde k es la probabilidad de encontrar una partícula abrasiva del punto de contacto entre las superficies y varía en un rango de entre 10−2 y 10−7 [19].
Los métodos para calcular el desgaste por abrasión en varios elementos de máquinas de la Ecuación (9), los cuales fueron probados experimental y abiertamente por la comunidad científica, reconociendo la naturaleza del desgaste por fatiga, finalmente, se toma se tomará como referencia la ecuación Kraglesky.
Donde V es la velocidad de desgaste medida en [um/h], A es el parámetro que caracteriza el material abrasivo, K es la caracterización de las condiciones geométricas del punto de contacto de las superficies deslizantes y M se encuentra en función de las propiedades del material de las superficies [3].
A partir de estas consideraciones se obtiene la ecuación base para medir la velocidad de desgaste de engranajes rectos y helicoidales.
· Ecuación de Archard: Velocidad de desgaste engranaje recto [3] (10).
· Ecuación de Archard: Velocidad de desgaste engranaje helicoidal [3] (11).
· Velocidad de desgaste abrasivo Kraglesky (12).
Las variables necesarias para caracterizar a la ecuación de Kraglesky de la ecuación (12) se dividen en tres parámetros, el término correspondiente a la partícula abrasiva, donde las propiedades mecánicas, tamaño y composición del material abrasivo modifican las características de la misma en función de la ecuación (13) [20].
· Propiedades de la partícula abrasiva Kragelsky.
Siguiendo el mismo contexto el factor (M) de la Ecuación (14) se relaciona con las propiedades mecánicas del material base, es directamente proporcional a la dureza y el porcentaje de elongación del material que se desea analizar, se toma como dato del abrasivo los valores de la Tabla 2 [20].
· Parámetro propiedades mecánicas del material Kragelsky (14).
Donde: ϵ t0 corresponde al porcentaje de elongación del material antes de la ruptura, t es un parámetro adimensional característico del contacto entre cuerpos y HB son las correspondientes durezas de los materiales que formen el par tribológico del proceso medido en escala Brinell. Finalmente, en el factor (K) se involucran todas aquellas condiciones geométricas y de forma que varíen el contacto entre las superficies, como el tipo de piezas, tamaño de las mismas, y condiciones de lubricación y distribución de fuerzas de contacto entre los elementos del par tribológico, es por eso por lo que se establece para engranajes rectos la ecuación (15) y para engranajes helicoidales la ecuación (16) [20].
· Engranaje de dientes rectos
· Engranaje helicoidal
Por lo tanto, el cálculo de la velocidad de desgaste por abrasión se resume de la siguiente manera, según Kraglesky con las ecuaciones (17) y (18).
· Ecuación de Kraglesky: Velocidad de desgaste engranaje recto
· Ecuación de Kraglesky velocidad de desgaste engranaje helicoidal
2.6. Proceso de ejecución de designación de variables para el cálculo de la velocidad de desgaste por la abrasión
Para el cálculo de la velocidad de desgaste por abrasión en ruedas dentadas se utilizó la ecuación de Archard de desgaste como primera aproximación. Posteriormente, se utiliza el modelo matemático formado por Kragelsky, Ecuación 3, donde nos indica el resultado más cercano al valor real. Se programan ambos métodos en una versión beta del software diseñado con la herramienta gráfica de Matlab, se generan resultados, se prueba la aplicación de cálculo, se varía cuestiones de forma y se busca la manera de que sea lo más amigable posible para el usuario.
Finalmente, con todas las correcciones encontradas en el proceso se programa la versión final de la aplicación, se compila para hacerlo independiente de Matlab y se generan los gráficos de resultados con ayuda de Excel con los datos obtenidos al variar las variables, parámetros de las ecuaciones. Como paso final se crea un manual de usuario del software y se presentan los resultados.
2.7. Declaración de variables
En función de las necesidades de datos de las ecuaciones y para tener claro los nombres de las variables que serán utilizadas en el proceso de programación, en este apartado se detallará el símbolo y el nombre de cada una de ellas.
ϑ (theta)= ángulo de presión
ψ (psi)= ángulo de hélice
z1= número de dientes engranaje 1
z2= número de dientes engranaje 2
m= módulo de los engranajes
P= potencia de la máquina
H1= Dureza material 1(Brinell)
H2= Dureza material 2 (Brinell)
Karch = constante del proceso ecuación de Archard
n = velocidad angular
rg = tamaño de grano promedio de la partícula abrasiva
cv = concentración en volumen de la partícula abrasiva
Eo1 = porcentaje de elongación material del engranaje 1
Eo2 = porcentaje de elongación material del engranaje 2
3. Resultados y discusión
3.1. Resultados
3.1.1. Versión App
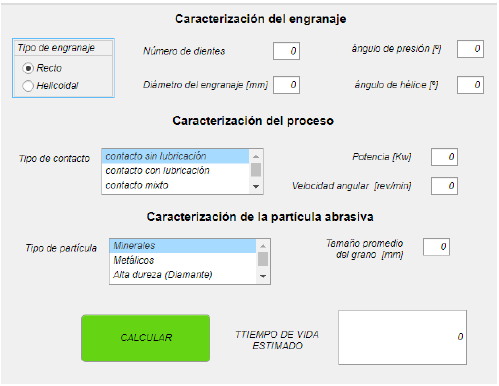
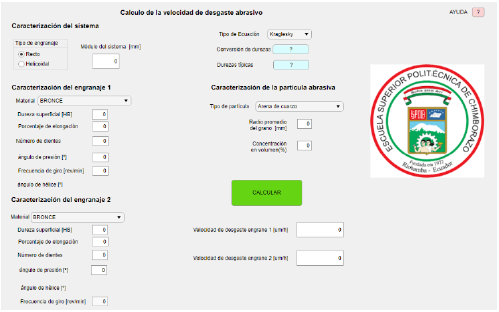
Al ingresar a la app, se verifica la Figura 7, se debe elegir el tipo y parámetros conocidos del engranaje. La interfaz permite una vista clara de los requerimientos, como el número de dientes del engranaje, el diámetro del engranaje, el ángulo de presión, el ángulo de hélice, el tipo de engranaje, la potencia requerida, la velocidad angular, entre los factores más importante para el registro de datos para el cálculo.
Posteriormente, se evalúan las entradas y salidas necesarias del sistema para cada una de las ecuaciones, como muestra la Figura 8. Se plantea el segundo modelo de versión de prueba, tomando en cuenta detalles que mejoren la experiencia del usuario, como un botón de ayuda, tabla de conversión de unidades y otros factores que no permitan cometer errores de formulación innecesarios. Es decir, se busca evitar datos repetitivos, o minimizar la entrada de datos si los valores necesarios pueden calcularse a partir de los ya obtenidos.
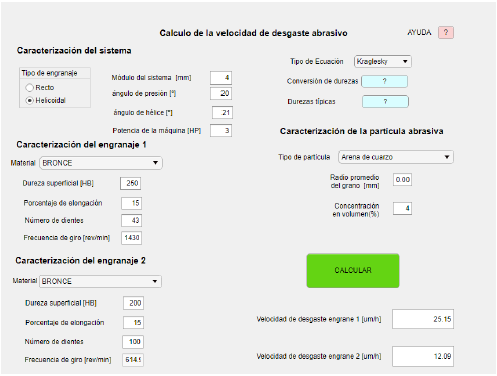
Sobre la base de las variables necesarias y las demandas requeridas para el correcto funcionamiento del software planteado para el cálculo de velocidades de desgaste de ruedas dentadas por abrasión con los métodos de Archard y Kraglesky se muestra la siguiente interfaz final, con el propósito que sea amigable para el usuario y tenga un aspecto agradable a la vista, como lo especifica la Figura 9.
3.1.2. Realización de toma de datos finales
Para este punto, se busca una comparación de los modelos matemáticos y tener en cuenta sus diferencias para comparar los resultados para los casos de gráficas con engranajes rectos y helicoidales, de esta manera, se pueda apreciar una tendencia en los modelos para asegurarse que no haya datos con notables errores y comprobar la validez del modelo en cada caso. De tal manera se limita los casos aislados y se entiende en qué momento y en qué condiciones es pertinente utilizar cada uno de los modelos planteados.
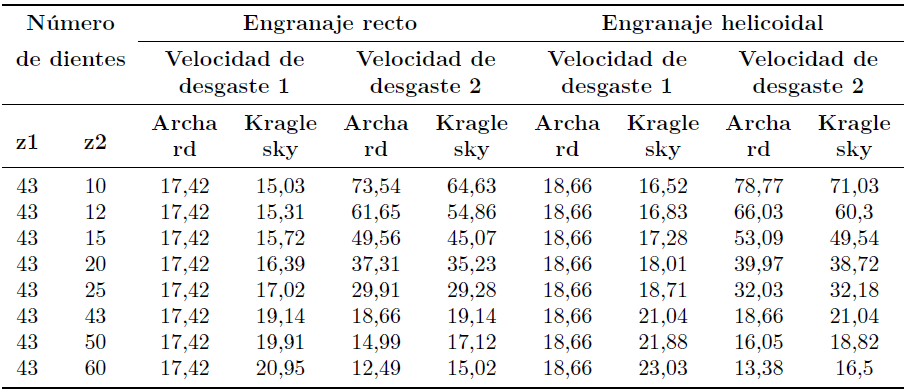
Para ello se tomarán dos sencillos análisis, el primero de ellos mostrado en la Tabla 3 en donde se varía el número de dientes de uno de los engranajes y se pretende calcular la velocidad de desgaste tanto en el caso de engranajes rectos y engranajes helicoidales para cada una de las ruedas dentadas involucradas en el proceso.
Se mantienen constantes las durezas y el porcentaje de elongación del material base de ambas ruedas en 250 HB y 18 %, también se mantiene fija la frecuencia de la rueda dentada uno en 1430 rpm. El módulo del sistema se fija en 4 y los ángulos de presión en 20 y 21 grados respectivamente.
Para el uso de la ecuación de Archard se toma como potencia promedio de la máquina a evaluar 200 HP. En cuanto a la caracterización de la partícula para la ecuación o modelo de Kraglesky, se usa arena de cuarzo con un tamaño de grano promedio de 0.05 mm y 4 % de concentración en volumen en el medio que los rodea [20].
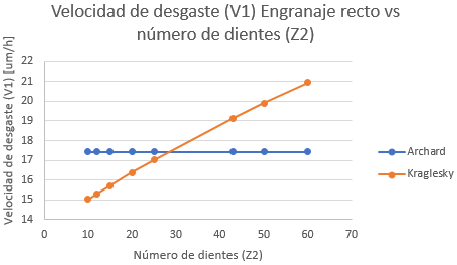
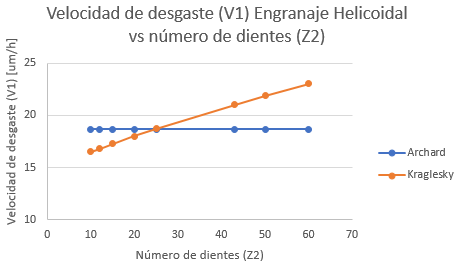
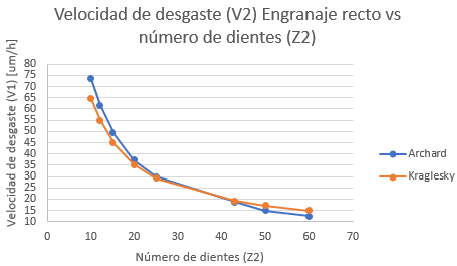
En la Figura 10 y Figura 11 se determinan los valores del desgaste de los engranajes rectos bajo las especificaciones de las variables indicadas anteriormente, donde al cambiar los valores se hallan los datos que son graficados en la hoja de Excel para poder manejar adecuadamente los parámetros de aproximaciones, tomando en cuenta de que la ecuación de Kraglesky es la ecuación matemática adecuada para los análisis manejados por el acercamiento a los valores por la variabilidad de los datos.
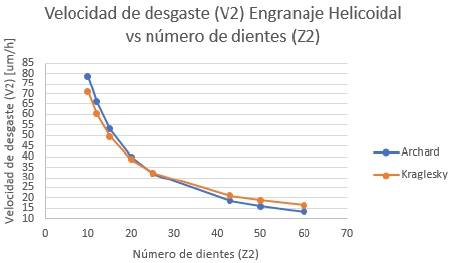
Se realiza un símil de los engranajes helicoidales y graficados en una hoja de Excel como se indica en la Figura 12 y Figura 13.
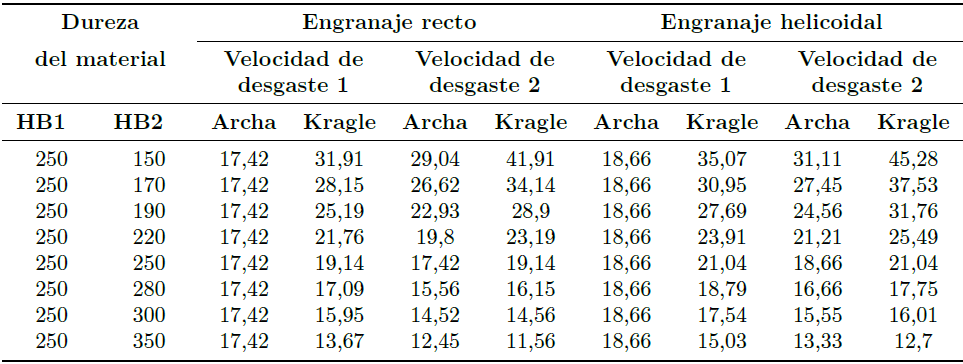
Para el segundo caso de análisis se tomarán los datos previamente planteados, con la diferencia que se mantendrán fijos los números de dientes de los engranajes involucrados en 43 y se varía la dureza superficial del segundo engranaje. Se calculará de igual manera la velocidad de desgaste para cada engranaje en el caso que sean rectos y helicoidales. De esta manera, se detallan los datos indicados en la APP finalizada, donde se precisa de otra comparación en función de la resistencia HB2 (Tabla 4).
3.2. Discusión
Ante las aproximaciones reales que se realizan, se toma en cuenta el proceso propuesto [4] de un esquema basado en vibraciones para actualizar un modelo de predicción de desgaste. Se desarrolla en primer lugar un modelo dinámico de un sistema de engranajes rectos para generar vibraciones realistas, lo que permite un estudio cuantitativo de los efectos del desgaste de la superficie de los dientes del engranaje.
La velocidad de deslizamiento y las fuerzas de contacto del modelo se utilizan en combinación con el conocido modelo de desgaste de Archard para calcular la profundidad de desgaste en cada punto de contacto en la malla. El perfil de los dientes del engranaje desgastado se retroalimenta en el modelo dinámico como un nuevo error de transmisión geométrica, que representa la desviación del perfil de una curva evolvente ideal y, por lo tanto, es cero para engranajes perfectos.
Dado que el coeficiente de desgaste en el modelo no es constante durante el proceso de desgaste (y en cualquier caso es difícil de estimar inicialmente), las vibraciones medidas se comparan con las generadas por el modelo, para actualizar el coeficiente cuando se detecta una desviación de las predicciones.
3.2.1. Datos para el cálculo
Para la determinación del proceso de evaluación se toma en cuenta los datos del siguiente estudio:
Acero dulce AISI 1045
Módulo: 4
Ángulo de presión: 20
Potencia: 4Kw (5,3641 HP)
Dureza: 163 HB
Porcentaje de elongación: 16
Número de dientes: piñón 19 engranaje 52
Frecuencia: 6000rpm
Promedio de grano: 0,05
Concentración de volumen: 1,85 [4]
La Figura 14 muestra los valores determinados en el paper en análisis donde especifica los valores del modelo experimental y del modelo de Archard, calculado por los autores de donde se obtiene los datos para la ejecución del análisis entre un proceso experimental ejecutado y el cálculo aplicado por medio de nuestra APP en Matlab.
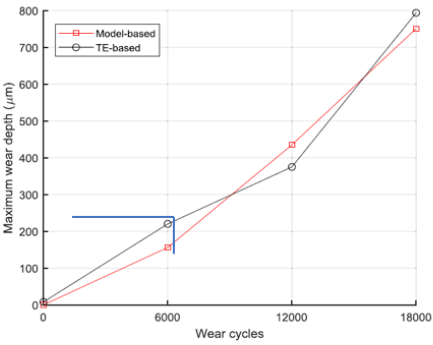
Figura 14. Resultados de la comparación de la profundidad máxima de desgaste: experimento y modelo [4]
3.2.2. Evaluación del modelo experimental del paper con el modelo de Kragelsky en la App de Matlab
En esta parte se determina el cálculo del porcentaje de error para verificar la coincidencia de los datos de la aplicación de la ecuación de Kragelsky con los datos del modelo experimental, para graficar el modelo del análisis de la predicción de desgaste abrasivo con el uso de vibraciones.
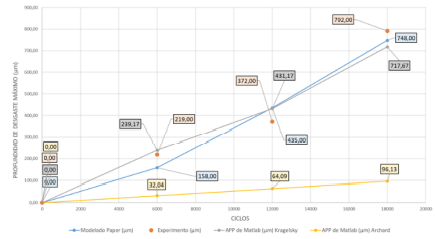
Se ejecuta un análisis primario entre un modelo matemático (línea azul) y el parámetro experimental (puntos anaranjados). Se adjuntan los datos de cálculo del modelo matemático utilizado en la presente investigación, que es el de Kragelsky (línea ploma), y la ecuación de Archard (línea amarilla). Estos datos se muestran graficados en la Figura 15.
Por lo expuesto, se tomará en cuenta y se verificará si los datos que se calcularon mediante la aplicación de Matlab se encuentran dentro de los rangos permisibles para que sean los adecuados al comparar las dos situaciones: la ecuación de Kraglesky y los datos del experimento.
Para el cálculo estadístico se toma en cuenta el proceso de la realización del error medio cuadrático, ya que este procedimiento es un estimador que ayuda a medir el promedio de los errores al cuadrado, es decir, se analiza la diferencia entre el estimador y lo que se estima. Siendo esta función como un evaluador de riesgo correspondiente al valor esperado de la pérdida del error al cuadrado o pérdida cuadrática. La diferencia se produce debido a la aleatoriedad o porque el estimador no tiene en cuenta la información que podría producir una estimación más precisa (ecuación (19)).
Con la Ecuación (19) del error medio cuadrático se procede a realizar el cálculo de la diferencia del proceso de aleatoriedad para producir una estimación más precisa. Los datos seleccionados donde se especifican los valores que se van a utilizar para la determinación de la perdida esperada.
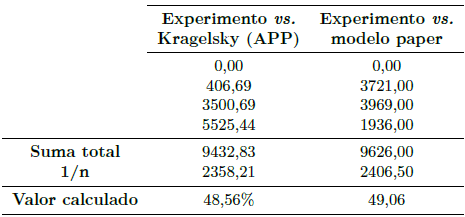
En la Tabla 5 se establecen los valores de cálculo en los cuales se especifica la efectividad de acercamiento a los datos del experimento; prueba de ello se establece que el manejo del modelo matemático de Kragelsky para la predicción del índice de desgaste es efectiva con un 48,56 %, interpretando de que los datos que se calculan ingresan dentro del rango de los valores del experimento de desgaste. Conviene especificar que el modelo matemático del paper brinda un valor del 49,06 % de aproximación a los valores experimentales.
Por otro lado, se presenta el análisis de la ecuación de Archard para la identificación de los valores calculados; en la Figura 15 se puede observar que los datos salen de los parámetros indicados y la desviación de los valores están lejos de acercarse, indicando un error del casi 90 %.
Hay que destacar que en el análisis se interpreta que la efectividad de la ecuación de Kragelsky es superior a la de Archard, ya que poseen datos que engloban el tamaño y porcentaje de abrasivo; es por eso por lo que la efectividad de los datos es sumamente factible para que se tome en cuenta en la determinación del índice de desgaste en elementos mecánicos.
4. Conclusiones
Se ha seleccionado dos modelos matemáticos de Archard y Kraglesky, se ha identificado correctamente las variables necesarias y la utilidad de cada uno de estos para la determinación del cálculo de la velocidad de desgaste por abrasión; tomando en cuenta el análisis con el paper de estudio y el análisis del error cuadrático realizado entre los valores obtenidos del experimento y las ecuaciones, se obtiene que el dato más adecuado es el de Kragelsky con un 48,56 % de error con relación al 49,06 % que emite el error cuadrático del modelo matemático del paper vs. los datos del experimento. Donde las limitaciones de la presente investigación son que los datos que se emiten o se necesitan para el cálculo deben ser obtenidos después de ejecutar el diseño del elemento y con el material al cual se encuentra construido.
Para la herramienta gráfica construida con la ayuda de la aplicación gráfica de usuario (GUIDE) de Matlab, se logró que cumpla con los requisitos necesarios para calcular la velocidad de desgaste abrasivo en ruedas dentadas, al tener lo más claro posible las variables que debe ingresar el usuario como los datos del tipo de abrasivo a analizar, la programación acorde con los modelos matemáticos en estudio; logrando evitar errores no intencionales, y tener opciones de ayuda para el usuario para conocer variables desconocidas para el usuario.
Los resultados obtenidos con el software pudieron ser tabulados, y graficados en Excel para comparar la tendencia de los mismos, como se presentó en el apartado de resultados, de manera que se establece que al ejecutar variabilidad en los datos se puede establecer la mejor decisión para diseñar un engranaje bajo características específicas y que el diseñador posea datos que pueden mejorar la funcionalidad del elemento mecánico que se diseñe tomando en cuenta el abrasivo que se encuentra en el ambiente.
Con la comprobación de los datos encontrados en la app y la experimentación, además de la explicación brindada al respecto, se comprueba y queda claro que el software diseñado como producto de esta investigación, permite el cálculo de la velocidad de desgaste por abrasión en ruedas dentadas rectas o helicoidales con perfil evolvente. También establece datos de predicción para la toma de decisiones para la ejecución de programas de mantenimientos y de prevención de fallas catastróficas que perjudiquen el área de trabajo y personal a cargo de maquinaria. El aporte del software es que una herramienta para la determinación de la rapidez de los valores que necesita un diseñador mecánico para evaluar la construcción de un elemento mecánico; tomando en cuenta variables que se pueden encontrar en el proceso de la construcción de los engranajes.
Trabajos futuros
El complemento perfecto para el software obtenido es una base de datos a corto plazo con experimentos en engranajes y diferentes abrasivos que permitan corroborar los datos y del mismo modo calibrar las constantes de los procesos en diferentes condiciones de trabajo bajo régimen de lubricación y funcionamiento controlado, adicionalmente, valorar los datos con herramientas estadísticas para mejorar el porcentaje de error y que los datos sean los más cercanos al ejecutar un proceso experimental con el cálculo en la app de Matlab.