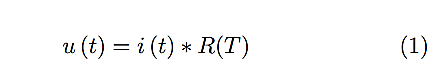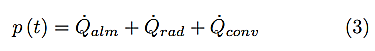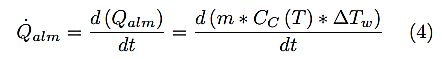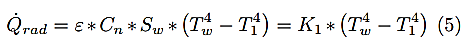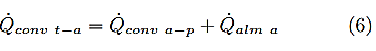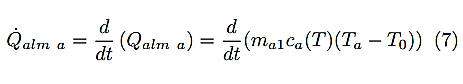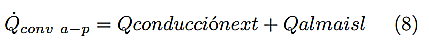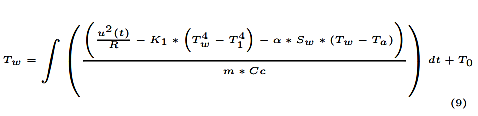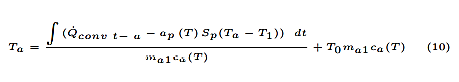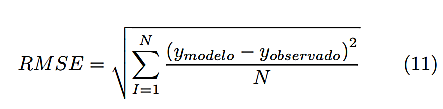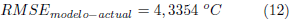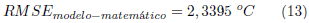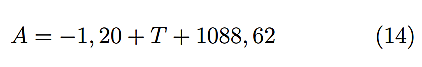Forma sugerida de citación:

Castro-Cepeda, L. y Cortés-Llanganate, J. “Modelo matemático de un horno resistivo para termoformado de láminas de polipropileno”, Ingenius, Revista de Ciencia y Tecnología, N.◦ 28, pp. 1-10, 2022. doi: https://doi.org/10.17163/ings.n28.2022.08

1. Introducción

La industria del plástico a nivel mundial ha crecido a través de los últimos años. Además de los datos de producción de materia prima virgen, esto se evidencia en el porcentaje de plástico que se recicla actualmente en los distintos países del mundo. En diez años el plástico tuvo un incremento del 80 % en el tema de reciclaje en los países europeos ^[1].

En Ecuador el plástico se utiliza en varios campos de producción, como son: la industria alimenticia (empaques de bebidas, snacks, etc.), industria de la construcción (techos traslúcidos, tejas plásticas, cortinas, etc.), utensilios de cocina en general ^[2]. Específicamente en la ciudad de Riobamba se encuentra localizada una industria, que se dedica a la fabricación de láminas traslúcidas de polipropileno, que sirven de complemento para los techos de fibrocemento.

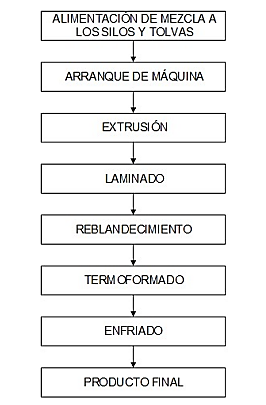
La planta posee tres líneas de producción que han sido montadas con tecnología reciclada, proveniente de países como España; después de que ya han cumplido su ciclo de vida útil se adquieren a precios menores para su reutilización. Luego en industrias locales, se repotencia haciendo algunas adecuaciones e incluso mecanizando partes y piezas que se acoplen al sistema para que funcionen con la mayor eficiencia posible. El proceso para la transformación del polipropileno se resume en la Figura 1.

Figura 1. Proceso de Transformación del polipropileno 

La máquina principal de esta línea es la que produce láminas de polipropileno tipo P7, lo cual se realiza en una termoformadora. El presente trabajo de investigación se ha desarrollado sobre el horno de entrada de la mencionada máquina termoformadora de plástico.

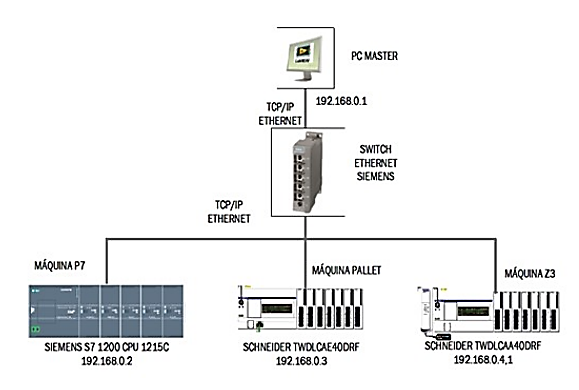
El primer trabajo consistió en establecer un sistema SCADA para el control de temperatura. Este se basaba en un sistema de control por histéresis, en donde las resistencias de la máquina en general se encendían y luego se apagaban cuando llegaban al valor deseado de temperatura ^[3]. Hoy en día el sistema descrito está en uso para la zona de extrusión, distribución y hornos de salida. En la Figura 2 se muestra la arquitectura de red utilizada en el sistema SCADA.

Figura 2. Arquitectura de red de área local de las máquinas ^[3]  

El segundo trabajo consistió en el diseño de un controlador para el horno de entrada basado en la identificación de sistemas. Con ello se obtuvo la función de transferencia del horno. Una vez identificada dicha función, se calculó un controlador PI para su control ^[4]. Este sistema es el que, actualmente, está siendo usado en la planta de producción para controlar el horno de entrada.

El sistema, hasta el momento, no ha sido modelado matemáticamente, por lo que se desconoce el comportamiento real de sus variables. Por lo tanto, se ha visto necesario encontrar este modelo matemático, el cual será comparado con los modelos existentes. Basándose en ellos se sugerirán modificaciones en el controlador que mejoren la calidad del producto. Hoy en día el producto cumple la normativa vigente del país, pero se observa que no es completamente uniforme en cuanto a su ancho. Al apilarlo para su distribución y venta genera al comprador una sensación y percepción que las planchas no cumplen con la normativa, por la variabilidad de dimensiones. Por lo tanto, el principal problema de este horno es que produce planchas con un ancho muy variable y que ocasiona que ciertos clientes no acepten el producto.

De las investigaciones analizadas, ^[5, ⁶, ⁷, ^8] Neacă y otros utilizan los fenómenos de transferencia de calor, para cuantificar la temperatura a través del modelo matemático encontrado, que para este caso de estudio, es similar. Sin embargo, cada publicación se distingue, pues todo su sistema está conforme a las características particulares de cada horno. Throne ^[9], ^[10], en cambio, basa su estudio en dos variables: la absortividad y emisividad, haciendo hincapié que son fundamentales en el desarrollo del modelo. Siguiendo la recomendación de este autor, se usará los datos adecuados en el análisis de la radiación, que se detallan en el planteamiento de la solución.

Mientras que Khan ^[11], Erdogan ^[12] y Chy ^[13], incluyen en sus trabajos investigativos propiedades específicas como densidad, difusividad térmica, espesor, calor específico y conductividad térmica, datos que también serán considerados en el desarrollo de esta investigación, para el análisis de conducción y convección, considerando la accesibilidad que se tiene al equipo y las características que se detallan en la descripción de la estructura del horno.

Por otra parte, Schmidt ^[14] y Ajersch ^[15] utilizan sensores infrarrojos, por lo que su estudio está direccionado al análisis por radiación. Estas publicaciones obtienen resultados que se ajustan a la realidad, sin embargo, por las condiciones experimentales del horno en estudio no es posible replicar esta técnica. Aunque servirá para comparar y discutir los resultados al final de la investigación. Chy y Boulet ^[16] dividen en capas el material a ser calentado, y luego interpretan los resultados como un solo elemento a través de técnicas numéricas, condición que no es posible realizarla en es este estudio, pero servirá para contrastar dichos resultados al momento de realizar las conclusiones.

Aunque todos estos investigadores desarrollaron modelos matemáticos aceptables del horno, en especial para la fase de calentamiento, aún existen algunas discrepancias entre la simulación, los resultados experimentales y las variables que cada autor utiliza en sus investigaciones, además que dichos modelos matemáticos se ajustan a las características propias de cada horno.

Por lo tanto, esta investigación pretende desarrollar un modelo mejorado para el horno, objeto de estudio y que se ajuste a sus características. Teniendo en cuenta de que el proceso se ejecuta principalmente a través de la intuición del operador de la máquina y su experiencia a través de prueba y error. Por ello nace la iniciativa de comprender el proceso de calentamiento del horno, haciendo especial énfasis en las características propias de su construcción, sabiendo que es un horno fabricado empíricamente. Con este modelo matemático se busca establecer una forma más precisa para predecir el perfil de temperatura dentro del horno que se usará en el futuro para un mejor control del proceso.

Existe un estudio previo realizado sobre el horno en análisis. En 2017, Cortés realiza la implementación de un sistema de control de temperatura para el horno de termoformado de la máquina denominada P7. Describe brevemente al horno mencionando que «está constituido por placas metálicas, las mismas que forma una cámara. Dicha cámara posee un aislamiento de lana de vidrio para reducir la irradiación del calor al exterior. En su interior se ubican resistencias tipo S y tipo U, conocidas así por la forma de las mismas, que son de distinta potencia eléctrica» ^[3]. El autor obtiene el modelo del horno mediante técnicas gráficas de identificación de sistemas, esto como un paso previo al diseño del controlador respectivo. Aplica varias técnicas, comparándolas entre sí. Al finalizar la validación respectiva, elige la que obtiene mayor porcentaje con el 90.95 %, que corresponde al método gráfico analítico sin retardo.

Sobre el modelo obtenido mediante identificación de sistemas, Cortés ^[4] obtuvo mediante los cálculos respectivos un controlador del sistema, que dio resultados aceptables con respecto a la variabilidad de la temperatura. Sin embargo, aún existe el inconveniente en el ancho de las planchas. El propósito de obtener el modelo matemático del horno en mención parece simple, pero llevarlo a la práctica resulta mucho más complejo, pues depende en gran medida de los datos con los que se cuenta. Con el fin de proporcionar un modelo del sistema que muestre el comportamiento dinámico real del horno y, de esta manera, permita realizar el cálculo de diversos controladores que finalmente optimicen su funcionamiento.

2. Materiales y métodos

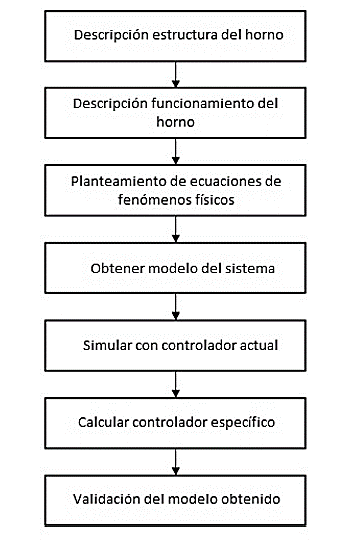
La metodología para desarrollar este trabajo de investigación se resume en el diagrama de la Figura 3 que se muestra a continuación:

Figura 3. Metodología de trabajo 

2.1 Descripción de la estructura del horno

El horno en estudio, que se muestra en la Figura 4, es de construcción local, con resistencias eléctricas óhmicas que por efecto Joule se calientan y ceden su calor. Ha sido construido con elementos, piezas de máquinas y equipos reciclados, que se acoplan entre sí para solventar las necesidades del proceso productivo. Para este caso específico, la producción industrial de planchas termoformadas usadas a nivel nacional en diversas aplicaciones. El horno está constituido por placas metálicas. Tiene forma de paralelepípedo, compuesto por dos cajas, una interior y otra exterior fabricada con láminas de acero galvanizado de 2 mm. Dichas cajas se encuentran separadas 5 cm una respecto a la otra. Entre placa se encuentra colocado el aislamiento. Para este diseño se usa fibra de vidrio, fabricada a partir de una mezcla de arenas, boratos y silicatos, cumpliendo así los parámetros recomendados por varios autores mencionados en el estado del arte. Por este motivo, de ahora en adelante, se supondrá que el horno posee el aislamiento necesario que evita pérdidas significativas que modifiquen el perfil de temperatura de este horno.

Figura 4. Horno de termofomado máquina P7 

2.2 Descripción de los fenómenos físicos del horno

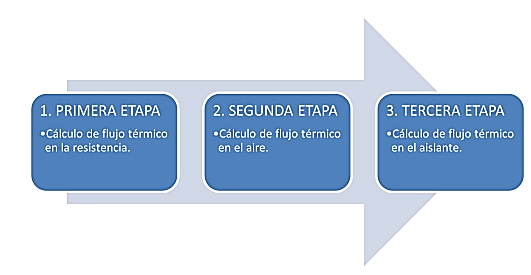
Para tomar medidas en el funcionamiento real de horno estudiado, se colocaron dos termocuplas tipo J, con el fin de medir la temperatura en el centro del horno y en una pared lateral, cada segundo durante el tiempo necesario en el que se llega a una estabilidad aproximadamente en 5000 segundos. Datos que se almacenaron en un computador conectado al equipo y que se usarán para obtener el modelo matemático, gracias a que el horno posee un sistema de adquisición de datos incorporado. Para que el estudio del horno sea más sencillo y práctico se ha dividido su funcionamiento en tres etapas las cuales se detallan en la Figura 5.

Figura 5. Diagrama de funcionamiento del horno 

En la Tabla 1 se muestra las nomenclaturas a utilizarse en las diferentes secciones del presente artículo.

Tabla 1. Nomenclatura utilizada en las diferentes ecuaciones 

2.2.1 Cálculo de flujo térmico en la resistencia

Se inicia con la transformación de energía eléctrica en energía térmica en la resistencia. Se parte fundamentalmente de la ecuación básica de la ley de Ohm (1).

El único elemento que interviene en el horno para transformar la energía es la resistencia, cuyos cálculos son fundamentales, pues al ser construida manualmente se desconoce. Para esto se usa la ecuación (2) en la que interviene la resistividad que depende de la temperatura, la longitud y la sección de la resistencia, datos que se pueden obtener fácilmente a través de mediciones, tablas y conociendo el material del que está construida.

Se aplica la ley de conservación de la energía en la termodinámica, que afirma que la cantidad de calor que recibe el sistema se transforma y realiza un trabajo en contra de fuerzas externas, como se muestra en la ecuación (3).

El flujo térmico almacenado en la resistencia se expresa mediante la expresión (4).

El calentamiento por radiación que se verifica en la ecuación 5.

2.2.2 Cálculo de flujo térmico flujo térmico en el aire

Después de realizar los cálculos respectivos con la resistencia, se continúa con las ecuaciones para el aire dentro del horno, con el fin de ir relacionado los fenómenos de transferencia de calor y desarrollar el modelo matemático esperado. Se parte de la ecuación en la que se relaciona el flujo térmico producido por la resistencia y el flujo térmico por el aire en la pared, dando como resultado el flujo térmico total, como se presenta en la ecuación (6).

El flujo térmico producido por el aire en la pared se expresa, usando nuevamente el fenómeno de convección. Posteriormente se calcula el flujo térmico almacenado en el aire que se expresa en (7).

2.2.3 Cálculo de flujo térmico en el aislante

Concluido el estudio de la transferencia de calor en el aire, se procede al análisis en el aislamiento. Para ello se utiliza la ecuación (8) en la que se define que el flujo de calor en la pared por el movimiento del aire, que es igual a la suma del flujo térmico transferido al exterior por conducción y el calor almacenado en el aislamiento mismo.

El horno posee una pared de aislamiento cuyo material es fibra de vidrio, por lo tanto, es necesario cuantificarlo, y para ello se usa el fenómeno de la conducción térmica. Se ha explicado, de manera general, las expresiones matemáticas y las definiciones que se utilizarán en la solución del modelo matemático; en el siguiente apartado se detallan los cálculos más importantes que alimentarán al sistema.

2.3 Planteamiento de la solución

Después de detallar los fenómenos físicos apoyados en la teoría clásica que se presentan durante el calentamiento del horno para el proceso productivo de termoformado, se procede con los cálculos matemáticos con el fin de obtener las ecuaciones diferenciales que permitirán encontrar el modelo matemático esperado. Con el fin de implementar de manera computacional la solución al problema planteado se usa la herramienta matemática Simulink, ya que es un entorno de programación visual que funciona sobre Matlab.

Para iniciar con los cálculos de la resistencia se usan los datos de la hoja técnica del material. Para ello se realiza una búsqueda dentro de los catálogos de la empresa para verificar específicamente que se tome la información correcta proporcionada por la empresa proveedora. En este caso el conductor utilizado es Nikrothal 70 ^[17]. Se realizan los cálculos adecuados que conducen la ecuación (9).

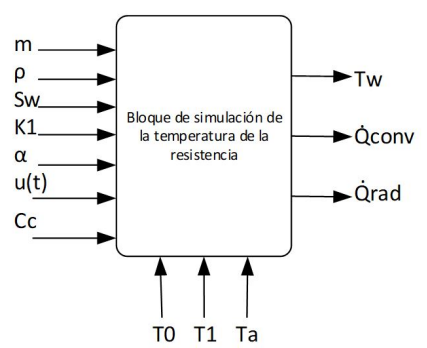
Esta ecuación se implementa en Simulink y visualiza el esquema de entradas y salidas en la Figura 6.

Figura 6. Esquema de entradas y salidas del cálculo de la temperatura de la resistencia 

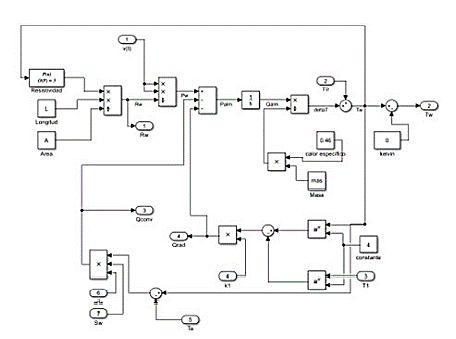
Se obtiene el comportamiento de la resistencia en función de la temperatura y con ello el calor que transforma a través de los fenómenos físicos ya descritos. Dicha implementación se puede observar en detalle en la Figura 7, que corresponde a la ecuación (9).

Figura 7. Esquema de entradas y salidas del cálculo de la temperatura de la resistencia 

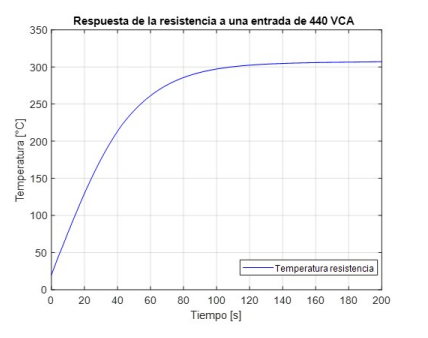
En la Figura 8 se observa la respuesta de la temperatura de la resistencia en función del tiempo al conectarla a un voltaje de 440 VCA, dicho perfil de temperatura se utilizará en el modelo del horno de termoformado.

Figura 8. Temperatura de la resistencia a lo largo del tiempo 

Finalmente, se calcula la temperatura del horno, dando lugar a la ecuación 10 que se implementa en Simulink. Dicha ecuación es el resultado de los cálculos matemáticos de las ecuaciones fundamentales de la termodinámica.

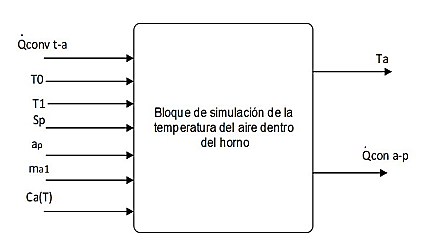
En la Figura 9 se observa el esquema básico que describe las entradas del sistema implementado en Simulink de la ecuación 10.

Figura 9. Esquema de entradas y salidas del cálculo de la temperatura del aire dentro del horno 

El cálculo de la temperatura en el aire dentro del horno, las ecuaciones y datos conseguidos a través de tablas y cálculos se implementan en Simulink. Este proceso se puede observar en detalle en la Figura 10, que corresponde a la ecuación (10).

Figura 10. Implementación de ecuación 10 

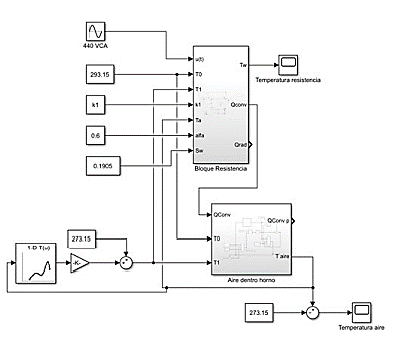
Teniendo el cálculo del flujo térmico de la resistencia y del aire del horno, el siguiente paso es calcular la temperatura que se pierde en el aislamiento y con ello obtener la temperatura que tiene la pared del horno. Al relacionar todos los cálculos se obtiene la temperatura del aire, dato que interesa conocerlo para su posterior procesamiento en los cálculos de sistemas de control. En el caso de la temperatura de la pared se utilizan valores obtenidos mediante el sistema de adquisición de datos del horno. En la Figura 11 se observa la implementación total del cálculo de temperatura en el aire del horno. Para ello se emplean los bloques ya calculados en los pasos previos.

Figura 11. Implementación total del cálculo de temperatura en el aire del horno 

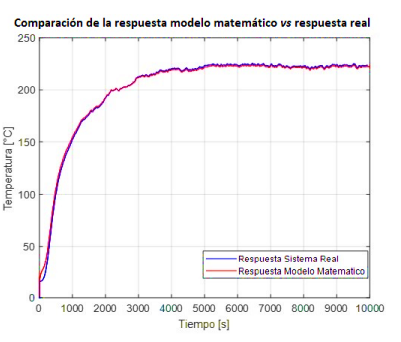
En la Figura 12 se observa la respuesta del modelo matemático comparándolo con la respuesta del horno obtenido mediante la adquisición de datos. Como se aprecia, el modelo se ajusta bastante bien a la curva real de funcionamiento. Lo que hace predecir que la validación del modelo matemático será mejor que la validación del modelo obtenido mediante técnicas de identificación gráficas publicadas por Cortés ^[4].

Para la obtención de la Figura 12 se ha aplicado una entrada del tipo escalón tanto al sistema real como al modelo matemático. En el sistema real se ha aplicado un voltaje de 440 VCA en las resistencias. En el modelo matemático de igual forma se ha aplicado un valor de 440 VCA. La adquisición de datos en el horno se lo realiza mediante la lectura de una termocupla tipo J, cuyo dato es muestreado en un periodo de un segundo.

Figura 12. Comparación de la respuesta modelo matemático vs respuesta real 

3. Resultados y discusión

3.1 Validación del modelo obtenido

Para validar el modelo matemático obtenido se utiliza técnicas matemáticas que permiten cuantificarlo. Este apartado se realiza desde varios puntos de vista, como se explica a continuación:

3.1.1. Comparación de la raíz del error cuadrático medio del modelo matemático vs modelo actual

La Figura 13 es similar a la Figura 12. Todas las curvas mostradas son las respuestas a una entrada del tipo escalón de 440 VCA. Se observa el comportamiento del sistema real en color azul, cuyos datos son tomados experimentalmente a través del sistema de adquisición de datos y han sido procesados en MATLAB. En color rojo se aprecia la respuesta del modelo matemático obtenido a través de los cálculos descritos en los apartados anteriores. La diferencia radica en que se muestra en color verde la respuesta a una entrada escalón 440 VCA aplicada al modelo por identificación gráfica que, actualmente, se utiliza en la planta para los cálculos del controlador. En esta gráfica se puede inferir que el modelo matemático se asemeja al perfil de temperatura real, por lo que se espera que al cuantificar el error este sea menor.

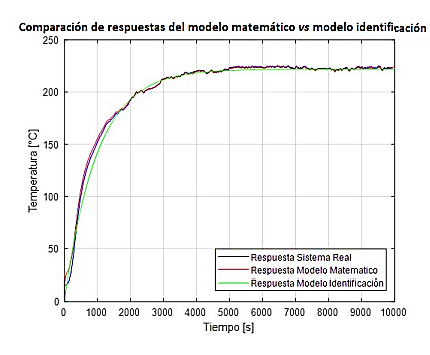
Figura 13. Comparación de las respuestas del modelo matemático vs el modelo calculado por identificación gráfica 

Para la primera validación se calcula la raíz cuadrada del error cuadrático medio RMSE ^[18], por sus siglas en inglés, cuya expresión matemática está representada por la ecuación (11).

Se calcula el valor de 2 RMSE de las respuestas a una entrada tipo escalón de 440 VCA:

• RMSE entre el modelo por identificación gráfica de sistemas que se usa actualmente para el cálculo del controlador y el sistema real cuyo resultado se representa en la ecuación (12).

• RMSE entre el modelo matemático encontrado en el presente trabajo de investigación y sistema real cuyo resultado se representa en la ecuación (13).

En el planteamiento de la solución se ha obtenido la curva que representa el modelo matemático real, pero es necesario compararla con los datos experimentales y, a su vez, con el modelo usado para el control actual en la máquina termoformadora.

De la comparación de los errores calculados se evidencia que el error del modelo matemático es menor que el del modelo actual, por lo tanto, el modelo matemático encontrado en este trabajo de investigación se ajusta con mayor precisión a la curva real del horno de termoformado.

3.1.2. Comparación de respuestas de control ante una entrada escalón

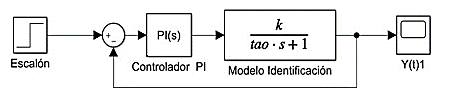
Se parte del sistema de control original que se visualiza en la Figura 14. Se introduce el modelo matemático en el sistema de control actual con el fin de analizar su respuesta, el valor del escalón (señal de entrada) es 140 ^o C.

Figura 14. Sistema de control de temperatura utilizando el modelo de identificación 

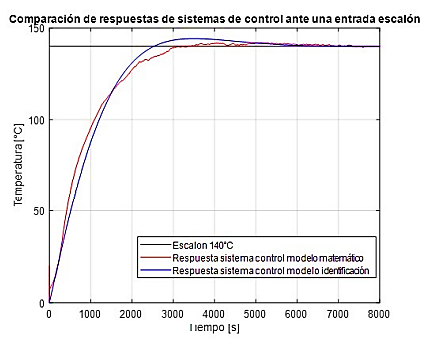
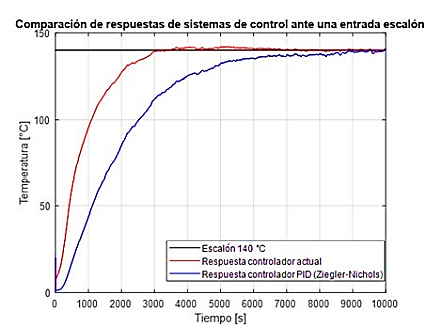
En la Figura 15 se observa la comparación de la respuesta del sistema de control con el modelo de identificación (línea azul) versus la respuesta del sistema de control con el modelo matemático (línea roja), y el escalón de 140 ^o C (línea negra). Se observa que las respuestas son diferentes a pesar de usar el mismo controlador, por lo que se puede interpretar que no es el adecuado para el modelo matemático, por lo tanto, se vuelve necesario hallar uno que se ajuste mejor a las características propias del modelo matemático, de esta forma, se espera que haya una mayor estabilidad en la temperatura y esto implícitamente conlleve a mejorar el producto terminado evitando los desajustes en el ancho de las planchas termoformadas.

Figura 15. Comparación de respuestas de los sistemas de control 

3.1.3. Cálculo de un nuevo controlador que se ajuste a las condiciones del modelo matemático, para simular y verificar su respuesta

Para calcular el nuevo controlador y simular la respuesta del sistema se aplica el método clásico de control de Ziegler-Nichols, pues es uno de los métodos más conocidos para la sintonización de los parámetros PID.

Sus reglas provienen de una respuesta experimental, según la dinámica del proceso y sin suponer algún conocimiento previo de la planta a controlar ^[19, ²⁰, ^21].

Figura 16. Cálculo PID por Z- N lazo abierto para modelo matemático 

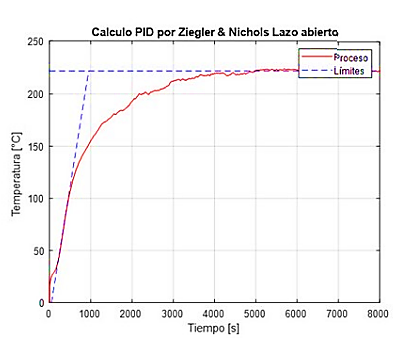
En la Figura 16 se observa los trazos de los límites que sirven para obtener los datos necesarios y, de esta forma, aplicar el método de Ziegler-Nichols de lazo abierto. Como se observa en la Figura 17, la respuesta del controlador PID utilizando el método de Ziegler-Nichols de lazo abierto no presenta mejoras en comparación con el sistema actual. Esto se debe a que el tiempo de estabilización (tiempo para llegar al valor consigna de control) es alto y la variación de temperatura no disminuye. Debido a esto es necesario calcular el controlador PID por otro método.

Figura 17. Comparación de la respuesta del controlador PID aplicado Z-N vs controlador PI actual 

La herramienta PID Tuner de Simulink proporciona un método de ajuste PID de lazo único rápido y de amplia aplicación para los bloques del controlador PID. Con este método, se puede ajustar los parámetros del controlador PID para lograr un diseño robusto con el tiempo de respuesta deseado.

En la Figura 18 se observa las respuestas del sistema de control, comparando el obtenido a través de la herramienta de Simulink PID Tuner en color azul con la respuesta del controlador actual en color rojo. Se verifica que este controlador genera una mejor respuesta del sistema llegando a una estabilidad de la temperatura en el menor tiempo posible, se ajusta mucho mejor dando una variabilidad de la temperatura menor. Hay que tomar en cuenta que los datos utilizados para el siguiente análisis son los que se encuentran a partir de los 4000 segundos, pues es ahí cuando el sistema se mantiene estable.

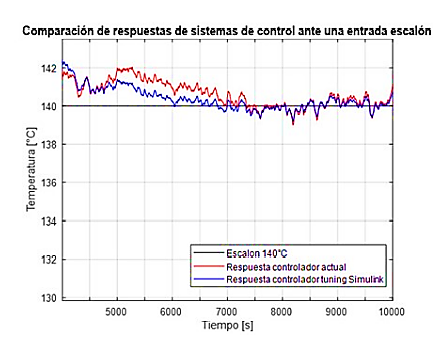
Figura 18. Visualización detallada de las respuestas de los sistemas de control actual vs controlador tuning 

A través de técnicas estadísticas se verifica el comportamiento de los datos para compararlos con los actuales y con ello cuantificar la mejora producida si se llegase a aplicar este controlador en el proceso productivo. La media de la temperatura del controlador actual es de 140,62 °C mientras que la media de la temperatura con el controlador propuesto en este trabajo es de 140,35 °C por lo que se evidencia cuantitativamente que se tiene una mayor estabilidad de la temperatura aplicando este controlador que usa el modelo matemático desarrollado. Además, se refleja en el error de la desviación estándar que para el controlador nuevo es menor. El 72,81 % de los datos simulados con el nuevo controlador son normales respecto a su media, mientras que tan solo el 65,55 % de los datos del controlador actual son normales respecto a su media; pero si comparamos los datos del controlador actual respecto a la desviación estándar del nuevo controlador apenas el 54,41 % de los datos son normales. De esta forma, se identifica que el nuevo controlador proporciona mejores resultados al sistema, por lo que si se lo implementa se garantiza una mayor estabilidad de la temperatura.

Se realiza un análisis de regresión lineal con datos suministrados por el departamento de calidad, con lecturas de temperatura y el ancho de las planchas termoformadas, con el fin de obtener una ecuación y verificar la correlación de la temperatura en función del ancho, donde A representa el ancho y T la temperatura del horno, como se muestra en (14). Con este modelo matemático se calcula el ancho de la plancha con las temperaturas que se obtienen del sistema con el controlador actual y se realiza el análisis estadístico correspondiente.

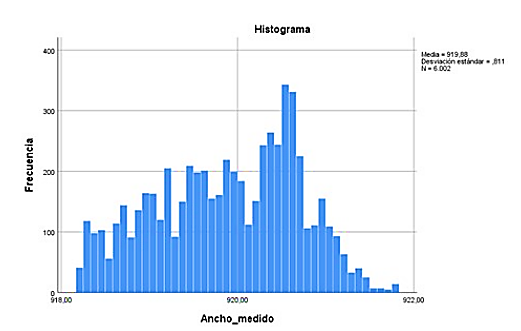
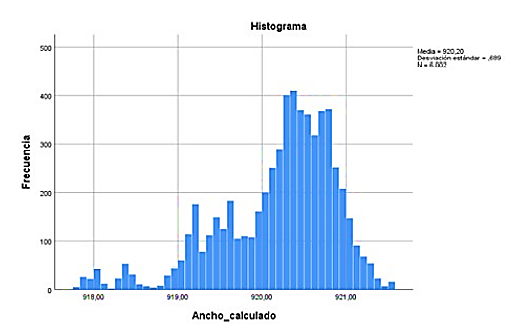
En la Figura 19 se observa el histograma de las planchas medidas, y se tiene una variación de ± 2 mm, además, se nota claramente que los datos son bastante dispersos. Por lo que las planchas son heterogéneas en cuanto a su ancho y al momento de apilarlas da la sensación de incumplimiento de la norma.

Figura 19. Histograma del ancho medido de las planchas termoformadas 

Por otra parte, en la Figura 20 se muestra el histograma de las planchas calculadas con el modelo de regresión lineal usando el sistema con el controlador propuesto y se observa claramente que existe menos dispersión de datos y se tiene una variación de ± 1 mm, con lo que se supondría que al apilarlas se verá de manera homogénea, generando seguridad al cliente en cuanto a la calidad del producto. Aunque sería importante tener datos experimentales que corroboren los datos obtenidos en este trabajo de investigación.

Figura 20. Histograma del ancho calculado de las planchas termoformadas 

De esta forma, se valida el modelo matemático y, a su vez, el nuevo controlador propuesto que se espera sea aplicado en la planta de producción y tener acceso a esos datos para con ello se confirme la eficacia de lo que en este documento se ha detallado.

4. Conclusiones

Se obtuvo el modelo matemático del horno resistivo para la producción de láminas termoformadas a partir del cual se calculó un nuevo controlador para el sistema. Se simuló su comportamiento y se proyectó la variabilidad del ancho de plancha, dando como resultado ± 1 mm a diferencia de la variación con el controlador actual que es de ± 2 mm. Dichos resultados muestran la efectividad del nuevo controlador.

Se consiguió el modelo matemático del horno. Para ello se dividió el funcionamiento en tres partes. En primer lugar, se formularon las ecuaciones que influyen en el calentamiento de la resistencia. Después, se expresaron las ecuaciones que inciden en el calentamiento del horno a través de la radiación y convección. Por último, se emplearon las ecuaciones que influyen en el calentamiento de la temperatura de la pared del horno. Sin embargo, la última parte no fue calculada debido a que no se cuenta con la información específica del aislante en las paredes del horno. En su lugar se usaron valores mediante el sistema adquisición de datos que posee el equipo.

Se encontró un modelo matemático que se ajusta mejor al funcionamiento real del horno. Esto se evidencia al calcular la raíz del error cuadrático medio del modelo matemático, que es menor en comparación al modelo obtenido por identificación de sistemas. Por lo que se concluye que el modelo matemático obtenido en este trabajo tiene una validación superior a la que se obtuvo en el sistema de control actual.

Se simuló un sistema que utiliza el controlador actual del horno acoplado al modelo matemático encontrado. Se evidenció que la dinámica de funcionamiento del horno es más lenta respecto a la simulación del sistema de control actual. Esto se debe a que el modelo matemático toma en cuenta distintos fenómenos que suceden, como la pérdida de calor en las paredes del horno. Por esta razón fue necesario calcular un nuevo controlador que se ajuste de mejor forma al modelo matemático.

Se determinó otro controlador que mejoró el comportamiento final del sistema. Sin embargo, este no fue obtenido mediante los cálculos tradicionales de controladores PID. En su lugar se emplearon técnicas de sintonización automáticas disponibles en Simulink (herramienta PID tuner). La principal diferencia está en que el controlador no es calculado en los términos de comportamiento inicial deseados por el usuario (sobre oscilación 2 %, tiempo de estabilización 3600 segundos). La sobreoscilación, en este caso, es de aproximadamente de 3,5% y tiempo de estabilización de 4000 segundos.

Se realizó la validación del modelo matemático obtenido por medio del análisis de datos del ancho de las placas de polipropileno. Para ello fue necesario calcular una función que relacione la temperatura con el ancho de dichas placas. Al comparar los resultados de los dos sistemas (actual y nuevo), se concluye que el nuevo sistema de control tiene una variación de ± 1 mm, mientras el actual sistema de control tiene una variación de ± 2 mm.

Para obtener una mejor validación de los sistemas referentes al ancho de placas es necesario diseñar mejores métodos de registros de información, que almacenen la temperatura junto a las características dimensionales específicas en tiempo real. Es decir, conocer el ancho que tiene la plancha en el instante que el horno tiene un determinado valor de temperatura.

Para ello sería necesario implementar un sistema más complejo de adquisición de datos que incidiría directamente en costos de producción, lo que, por el momento, no es factible en la planta de producción.