Forma sugerida de citación:
Lampier, L. C.; Coelho, Y. L.; Caldeira, E. M. O. y Bastos-Filho, T. F. “Un enfoque de aprendizaje profundo para estimar la frecuencia respiratoria del fotopletismograma,” Ingenius, Revista de Ciencia y Tecnología, N.◦ 27, pp. 96-104, 2022. doi: https://doi.org/10.17163/ings.n27.2022.09.
1. Introducción
La frecuencia respiratoria (Respiratory Rate, RR) es un indicador importante del estado fisiológico de una persona, de manera especial en el monitoreo de enfermedades pulmonares. Esta señal fisiológica se mide tradicionalmente por medio de una espirometría, neumografía o electromiografía [1]. Estas metodologías son costosas y utilizadas en ambientes médicos. La fotopletismografía (Photoplethysmography, PPG) es una técnica que mide la frecuencia cardíaca utilizando un oxímetro, mucho más económico que los métodos tradicionales de medición de la RR. Estudios recientes muestran que puede ser captada aun remotamente utilizando la cámara de un teléfono inteligente [2]. Considerando que la respiración tiene influencia sobre los ciclos cardíacos, la información de la RR también se presenta en la señal PPG [3].
Varias metodologías reportadas en la literatura han estimado exitosamente la RR con un error pequeño a partir de la señal PPG [1], [4, 5, 6, 7, 8], sin embargo, la atenuación del ruido es todavía un reto para obtener predicciones robustas a partir de señales PPG de baja calidad. Este artículo presenta una manera alternativa para inferir la frecuencia respiratoria a partir de señales PPG. Las técnicas de aprendizaje profundo (Deep Learning) han sido ampliamente utilizadas en problemas de procesamiento de imágenes, sin embargo, también son una herramienta poderosa en problemas de una dimensión (1D), limitadas principalmente por el tamaño y la calidad del conjunto de datos, y también por el poder computacional disponible durante el proceso de entrenamiento. A medida que crece la data disponible en línea, así como también el poder computacional del hardware, las DNN están siendo probadas en una gran variedad de problemas que anteriormente estaban dominados por procedimientos analíticos.
Con respecto al procesamiento de señales PPG, Ravichandran et al. [1] mostraron que una DNN puede utilizarse para extraer la señal RR a partir de señales PPG. Biswas et al. [9] extraen el pulso a partir de la PPG utilizando una DNN. Este trabajo propone el uso de una DNN para extraer mediciones confiables de RR a partir de señales PPG, utilizando procedimientos analíticos para extraer señales secundarias de la PPG y una DNN para inferir la RR.
1.1. Trabajos afines
De acuerdo con Charlton et al. [10], los algoritmos PPG-RR pueden resumirse en cinco pasos:
Extraer las señales respiratorias. Consiste en encontrar la variación de la señal PPG relacionada a los ciclos respiratorios.
Fusionar las señales respiratorias. Las diferentes señales extraídas pueden combinarse para crear una señal única con mayor robustez ante el ruido (opcional).
Estimar la RR a partir de una ventana. Se segmenta una ventana de la señal generada y se estima la RR a partir de esa aquella.
Combinar las estimaciones. El resultado de diferentes ventanas puede utilizarse para generar una estimación final (opcional).
Filtrado de calidad. Puede asignarse un score de calidad a la ventana PPG, para excluir predicciones de baja calidad (opcional).
Algunos de los primeros enfoques que estiman la RR a partir de PPG utilizan dos filtros Butterworth de segundo orden, uno pasa-alto y uno pasa-bajo con frecuencias de corte 0,1 Hz y 5 Hz, respectivamente, para eliminar el ruido de la PPG. Luego se estima la señal respiratoria aplicando un filtro pasa-bajo de 0,4 Hz a la señal PPG [11]. Madhav et al. [12] aplicaron una relación de valor singular (Singular Value Ratio, SVR) para extraer la periodicidad respiratoria de la PPG, y utilizaron análisis de los componentes principales (Principal Component Analysis, PCA) para estimar la actividad respiratoria del primer componente principal. En otro enfoque propuesto por Nam y colaboradores [13], se capturó una señal PPG utilizando la cámara de un teléfono inteligente, y luego se estimó la RR encontrando la frecuencia correspondiente al pico más alto del espectro generado por el periodograma de Welch [7].
Se compararon cinco metodologías diferentes en el trabajo realizado por Pimentel y colaboradores [4], incluyendo la desarrollada por los autores. La más antigua fue propuesta por el equipo encabezado por Nilsson [14], y consiste en aplicar un filtro Bessel pasabanda de orden 16 con frecuencias de corte 0,13 Hz y 0,48 Hz (7,8 a 28,8 respiraciones/min). La segunda propuesta [8], utiliza la transformada de Fourier sobre la señal PPG y obtiene la frecuencia con la mayor amplitud en el ancho de banda entre 0,08 Hz y 0,4 Hz. En la metodología sugerida por Tarassenko [5], los modelos autorregresivos (AR) estiman un filtro utilizando la señal PPG, y de acuerdo con ellos la frecuencia del polo de mayor magnitud dentro del intervalo del ancho de banda de la RR (0,08 Hz a 0,7 Hz) corresponde a la RR. En lugar de utilizar la propia PPG [6] se estiman tres características temporales relacionadas con la RR: variación de la intensidad inducida por la respiración (Respiratory-Induced Intensity Variation, RIIV), variación de la amplitud inducida por la respiración (Respiratory-Induced Amplitude Variation, RIAV) y variación de la frecuencia inducida por la respiración (Respiratory-Induced Frequency Variation, RIFV). Luego, se calcula el espectro de potencia de cada una y se estima la RR a partir de cada una tomando la frecuencia de mayor amplitud en la banda de frecuencias de la RR (0,067 Hz – 1,08 Hz) y calculando la media de las tres frecuencias. Finalmente, la metodología mostrada por Pimentel et al. [4] combina el modelado AR propuesto en Tarassenko [5], con la fusión de resultados de las tres características propuestas por Karlen y su equipo [6].
Los resultados presentados [4] muestran que para el conjunto de datos CapnoBase [15], el método que presentó el error más bajo [6], es decir, con un error absoluto de la mediana (Median Absolute Error, MdAE) de 0,8 respiraciones/min utilizando una ventana de 62 s; sin embargo, 46 % de los datos de PPG fueron excluidos debido al ruido. El segundo mejor en este conjunto de datos fue el citado por Tarassenko [5], que alcanzó un MdAE de 1,1 respiraciones/min y conservó 92 % de la data. El conjunto de datos BIDMC parece ser más desafiante, debido a que el mejor MdAE fue obtenido por el método propuesto por Shelley [8] (2,3 respiraciones/min), el cual también fue uno de los métodos que conservó la mayoría de la data (94 %). Un trabajo reciente ha obtenido resultados aún más precisos [16], en el que un método deriva múltiples ondas de una señal PPG, mide su calidad y luego la utiliza como ponderación para combinarlas utilizando un suavizador de Kalman. Con este enfoque obtuvieron un error mediano de 0,2 respiraciones/min
1.2. Redes neuronales profundas (Deep Neural Networks, DNN)
Para Goodfellow et al. [17], el aprendizaje profundo es un enfoque que puede manejar un paso importante en un problema de aprendizaje de máquina: la extracción de características. Su concepto consiste en concatenar múltiples capas de modelos simples, donde cada modelo «aprende» parte de los problemas-conceptos y, por tanto, un problema complejo puede dividirse en modelos más simples para ser resuelto de mejor manera. Un punto interesante de este enfoque es que realiza las tareas de aprendizaje automático (clasificación, regresión, agrupamiento, etc.) y también la extracción de características, en contraste con las técnicas poco profundas, en el que el paso de extracción de características debe hacerse de manera separada, en una etapa previa, y exige conocimiento del área. La limitación del enfoque de aprendizaje profundo es el conjunto de datos. Normalmente, los modelos de aprendizaje profundo tienen un gran número de valores a ser ajustados y, por tanto, necesitan grandes cantidades de datos para optimizarlos.
Existen algunos enfoques que instrumentaron técnicas de aprendizaje profundo para resolver problemas relacionados con data fisiológica. Biswas et al. [9] implementaron una DNN para estimar la frecuencia cardíaca (Heart Rate, HR), teniendo como data de entrada una señal PPG obtenida de un sensor colocado en la muñeca del usuario. El modelo fue probado en un conjunto de datos desafiante, en el cual la señal PPG fue capturada durante varias actividades físicas, las cuales insertan ruido y artefactos en ella. La arquitectura del modelo estaba constituida por dos capas convolucionales de una dimensión seguidas de dos capas de gran memoria de corto plazo (Long Short-Term Memory, LSTM) y, finalmente, una capa densa. Esta arquitectura alcanzó un error absoluto medio (Mean Absolute Error, MAE) de 1,47 ± 3,37 latidos por minuto (Beats Per Minute, BPM).
En el trabajo [1] se presenta un enfoque de aprendizaje profundo para extraer la señal RR a partir de la señal PPG. Su modelo consta de varias capas convolucionales conectadas a varias capas deconvolucionales que transforman la señal PPG en la señal respiratoria, y luego calculan a partir de ella la RR. Su método fue probado en dos conjuntos de datos independientes, CapnoBase y Vortal [18], y alcanzó un error cuadrático medio (Mean Squared Error, MSE) de 0,262 en el primer conjunto de datos y de 0,145 en el segundo, lo que corresponde a una raíz cuadrada del error cuadrático medio (Root Mean Squared Error, RMSE) de aproximadamente 3,1 respiraciones/min y 2,3 respiraciones/min, respectivamente.
2. Materiales y métodos
2.1. Conjuntos de datos
En las pruebas se utilizaron dos conjuntos de datos: el benchmark CapnoBase [15] y el de respiración BIDMC PPG [19]. El primero consta de 42 registros [20], de 8 minutos cada uno, que contienen la PPG y la señal de dióxido de carbono (CO2) inhalado y exhalado, ambos recolectados a una frecuencia de muestreo de 300 Hz. El conjunto BIDMC PPG [21] contiene 8 minutos de registros de señales PPG y respiración de CO2 de 53 voluntarios, recolectados a 125 Hz.
2.2. Características respiratorias del fotopletismograma
A partir de la PPG se generaron tres señales relacionadas con la respiración [6]:
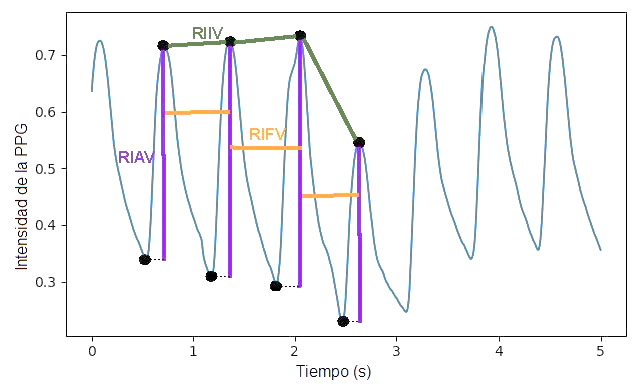
Variación de la intensidad inducida por la respiración (Respiratory-Induced Intensity Variation, RIIV). A medida que la amplitud de la señal PPG varía en sincronía con el ciclo respiratorio, esta característica puede utilizarse para estimar la RR [3]. Esta serie es estimada tomando el valor de la intensidad de cada pico en la señal PPG [4].
Variación de la amplitud inducida por la respiración (Respiratory-Induced Amplitude Variation, RIAV). Los ciclos respiratorios inducen una variación de amplitud en las ondas PPG, la cual puede estimarse calculando la variación en la diferencia pico-valle en las ondas PPG [6].
Variación de la frecuencia inducida por la respiración (Respiratory-Induced Frequency Variation, RIFV). La variación en la HR también está altamente ligada a los eventos respiratorios de inspiración y expiración. Las inspiraciones aumentan la HR y las expiraciones la reducen. Esta señal puede representarse por el intervalo de tiempo entre picos consecutivos de la PPG [6].
La Figura 1 muestra una representación gráfica de las características RIIV, RIAV y RIFV.
2.3. Índice de calidad de la señal (Signal Quality Index, SQI)
El SQI cuantifica la contaminación por ruido y artefactos en la ventana PPG analizada. Este índice se utiliza para excluir las señales que no alcanzan una calidad mínima. En este trabajo, el SQI se calcula abordando dos puntos: «líneas planas» en la señal, y concordancia entre diferentes detectores de picos [4]. Las «líneas planas» se definen como las partes de la señal PPG en las que la diferencia entre muestras consecutivas es cercana a cero. Para detectarlas se realizó el siguiente método:
-
La señal StdDiff es calculada como sigue: StdDiff [i−wdw] = σ(diff (PPG [i−wdw : i])),for i = wdw, wdw + 1,wdw + 2, .....,N.
Donde σ(.) es la operación que calcula la desviación estándar, diff (.) es la primera derivada de la operación, PPG es la señal PPG, wdw es la longitud de la ventana, que, en este caso, es la parte entera de 1,5 s × frecuencia de muestreo (1,5 s es el intervalo de tiempo entre picos consecutivos en el valor mínimo de HR, que normalmente es 40 BPM), y N es el número de muestras en la señal PPG.
Se inicializa el arreglo Q con unos y el mismo tamaño que la PPG: Q = ones(N)
Se calcula el valor umbral: th = µ(StdDiff) − α×σ(StdDiff)), donde µ(.) es la operación que calcula la media y α es un parámetro ajustable.
-
Los valores de k se hacen cero en las ubicaciones correspondientes donde StdDiff es muy bajo: for i = wdw, wdw + 1, wdw + 2.....N : {if (StdDiff[i − wdw] < (th) : { Q[i + wdw] = 0
}}
El valor K es la proporción entre los valores iguales a Q dentro de la ventana PPG analizada, y su tamaño total.
La concordancia entre dos detectores de picos fue realizada de la siguiente manera: si la diferencia entre la posición encontrada por los detectores en el mismo pico es menor que 150 ms, se considera que ambos detectores concuerdan en ese pico y, por lo tanto, su posición es correcta; de lo contrario, el pico se considera como un ruido [4]. Entonces se aplica un score F1 para medir la concordancia entre dos detectores de picos en el segmento analizado de la señal. Los métodos de detección de picos fueron proporcionados por dos librerías diferentes de Python: Neurokit2 [22], que implementa el algoritmo de detección de picos PPG descrito en [23] y la librería Heartpy [24], en la que los autores desarrollan su propia técnica de detección de picos.
Finalmente, el SQI se calcula como: SQI = F1×K, donde F1 es la concordancia entre picos y K es la proporción de «línea plana»
2.4. Arquitectura DNN
La arquitectura del modelo se inspiró es la CorNET [9], que tiene dos bloques convolucionales, cada uno de los cuales contiene una capa convolucional (32 filtros con un kernel de tamaño 40), una capa de normalización batch, una capa de activación con unidades lineales rectificadas (Rectified Linear Units, ReLU) y, finalmente, una capa maxpooling con un tamaño de pool de 4 (para el entrenamiento se utilizó una capa dropout con una tasa de eliminación (drop rate) de 0.1). Luego de los bloques convolucionales se concatenan dos capas LSTM, cada una con 128 unidades y función de activación tangente hiperbólica (tanh). Para la predicción se utilizó una neurona con activación lineal.
La arquitectura propuesta para predecir la RR es el resultado de la optimización mediante algoritmos genéticos, de los parámetros de la CorNET que se presentan en la Tabla 1.
Los parámetros mencionados arriba son optimizados, mientras que para los parámetros no mencionados se utiliza la definición por defecto en la librería Keras [25]. Considerando que el número de combinaciones es muy grande (2916), los parámetros se optimizan utilizando algoritmos genéticos. Esta estrategia comienza definiendo una población de L modelos con parámetros aleatorios, y luego todos los modelos son entrenados, probados y categorizados de acuerdo con el resultado. Los M modelos con mejor desempeño se conservan mientras que los otros se descartan. El conjunto de los modelos conservados se denomina padres, y luego se generan M − J nuevos modelos tomando valores de tres modelos diferentes (un padre para los parámetros convolucionales, uno para las capas LSTM, y otro para las capas densas). Adicionalmente, existe una probabilidad de H % de que los parámetros de los nuevos modelos cambien aleatoriamente (estos cambios se denominan mutaciones); estos nuevos modelos se denominan descendientes. Asimismo, existen J modelos nuevos generados de forma completamente aleatoria, y a este conjunto se le asigna el nombre de extranjeros. Luego, los conjuntos de padres, descendientes y extranjeros se unen comienza una nueva interacción.
El procedimiento se repite por E épocas (epochs). La idea es que los parámetros que disminuyen el error de estimación prevalezcan en el conjunto de padres, y su combinación pueda generar un modelo en el conjunto de descendientes que mejore el resultado de sus padres. Asimismo, nuevos parámetros aleatorios se insertan con las mutaciones y los extranjeros creados en cada iteración. Estas adiciones aleatorias establecen una posibilidad de que la población de modelos salga de un mínimo local subóptimo. Para este experimento, los parámetros de la optimización mediante algoritmos genéticos fueron los siguientes: L = 45, M = 20, J = 5, E = 20 y H = 20, lo cual redujo el número de modelos entrenados de 2916 a 520 (25 nuevos modelos/época × 20 épocas + los primeros 20 padres). El mejor modelo encontrado es una DNN con 2 bloques convolucionales con 32 filtros y un MaxPooling de una dimensión (tamaño de kernel 2) en cada capa convolucional, un tamaño de kernel de 21, y activación ReLU. Luego, una capa LSTM con 32 neuronas, y finalmente, 2 capas densas, una con 32 neuronas y activación ReLU y la última con una neurona y activación lineal. La Figura 2 presenta un resumen de la arquitectura DNN final.
2.5. Procedimiento de entrenamiento y prueba
Se utilizaron dos conjuntos de datos para entrenar y evaluar los modelos BIDMC [19] y CapnoBase [15]. Se empleó el método de validación cruzada con cuatro grupos: para cada base de datos, sus archivos se dividieron en cuatro grupos, cada uno de los cuales contenía el 25 % de los datos en cada conjunto. Luego, se realizó el mismo procedimiento en cada grupo: primero, se encontraron los picos de la PPG utilizando la librería Neurokit2 [22]. Posteriormente, utilizando una ventana deslizante de 64 s con un paso de 4 s, se calcularon las tres señales relacionadas a la RR (RIIV, RIAV y RIFV), que luego se interpolaron a una frecuencia de muestreo artificial de 4 Hz y se extrajeron las primeras 240 muestras (60 s) de la ventana, generando así una muestra con 240 líneas (pasos de tiempo) y tres columnas (correspondientes a RIIV, RIAV y RIFV). El paso final consiste en normalizar la data, de manera que cada canal de la nueva muestra tenga media 0 y varianza 1: Y = (X − µ(X))/σ(X), donde Y es la serie normalizada, X la serie de entrada, µ(.) es la operación que calcula la media y σ(.) es la operación que calcula la desviación estándar.
Para obtener el valor de referencia de la RR, se localiza el pico de CO2 correspondiente a cada muestra utilizando el módulo Respiratorio de Neurokit2, y luego se calcula la mediana de la RR de la muestra de 64 s, tomando la inversa del valor de la mediana en el intervalo de tiempo entre picos consecutivos.
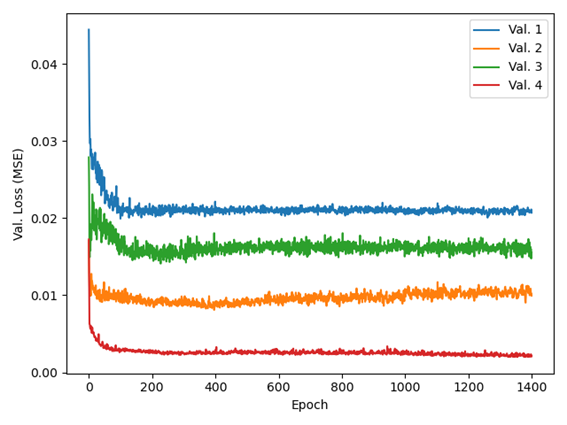
Posteriormente se dividen los cuatro grupos de muestras normalizadas en conjuntos de entrenamiento y prueba, donde el conjunto de entrenamiento tiene tres grupos y el de prueba tiene uno. Los procedimientos de entrenamiento y prueba se repitieron cuatro veces, para que cada grupo pudiera ser evaluado una vez en el conjunto de prueba. Cada uno de los 4 modelos (uno para cada grupo de prueba) fue entrenado por 1400 épocas utilizando el optimizador Adam con parámetros estándar de Keras [25]. El procesamiento se realizó en un computador Ryzen 5 3500X con 16 GB de memoria RAM y un NVIDIA GeForce RTX 2060 SUPER con 8 GB de memoria dedicada. Se utilizó la métrica del error cuadrático medio para calcular la pérdida (loss) en cada época. La Figura 3 presenta la curva de pérdida resultante.
Los grupos de validación 1 y 4 tuvieron una pérdida decreciente hasta la época 1400, el grupo 2 tuvo su pérdida mínima alrededor de la época 400 y el grupo de validación 3 tuvo su mínimo alrededor de la época 200, y luego decreció nuevamente después de la época 800. El gráfico se utilizó para determinar el número de épocas de entrenamiento de las DNN, dado que la mitad de los grupos de validación se mantienen decreciendo hasta la época 1400 y la capa dropout parece evitar el sobreajuste en los otros grupos, debido a que la pérdida no se incrementa mucho luego de los mínimos. El proceso se repitió revolviendo la data y los grupos, y entrenando cuatro DNN (una para cada grupo de entrenamiento-prueba) durante 1400 épocas para realizar la validación cruzada.
3. Resultados y discusión
La Tabla 2 y la Tabla 3 presentan el MdAE y la desviación estándar del error, así como también la raíz cuadrada del error cuadrático medio y el umbral SQI utilizado para filtrar las muestras ruidosas. Probando diferentes valores de SQI es posible analizar la influencia de la calidad de la señal en el resultado. Los resultados de MdAE alcanzados por nuestro modelo sobre el conjunto de datos CapnoBase son compatibles con los de las mejores metodologías comparadas [4], en las cuales el mejor MdAE para una ventana de 64 s fue 0,8 respiraciones/min, obtenidas utilizando el método [6]. Sin embargo, la metodología excluye el 36 % de las muestras que no alcanzan el mínimo SQI. El segundo mejor fue el método [5], alcanzando un MdAE de 1,1 respiraciones/min para el 92 % de las mejores muestras.
Para el mismo conjunto de datos, nuestro método obtuvo un MdAE de 1,16 respiraciones/min (calculado concatenando los resultados de todas las cuatro pruebas), y un MdAE de 1,11 respiraciones/min con el 93 % de las muestras con el SQI más alto. Sin embargo, el RMSE del modelo DNN propuesto no alcanzó el error del RespNET [1], que es 3,1 respiraciones/min, indicando que nuestro modelo todavía puede ser refinado para alcanzar mejores resultados.
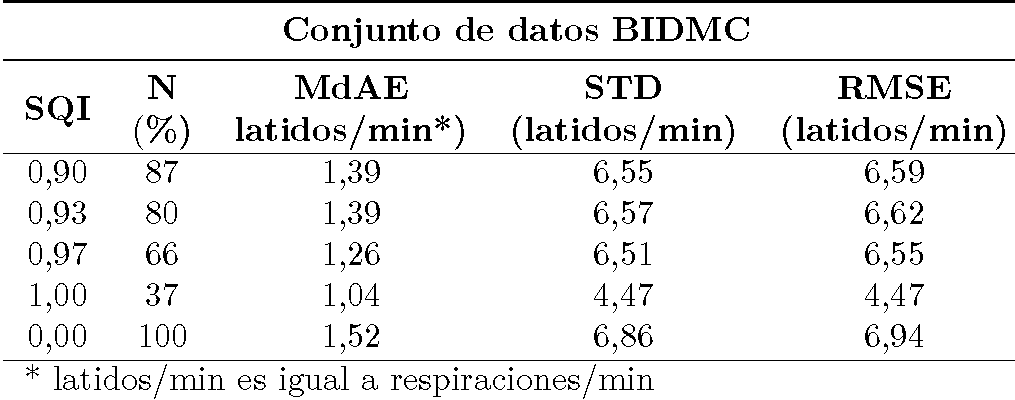
El modelo DNN propuesto alcanzó errores menores en el conjunto de datos BIDMC, que los otros métodos comparados [4]. Con todas las muestras, nuestro método obtuvo un MdAE de 1,52 respiraciones/min en este conjunto de datos, mientras que el error más pequeño obtenido [4] para este conjunto de datos fue para la metodología propuesta [8], con un MdAE de 2,3 respiraciones/min. Esta mejora en el resultado muestra el éxito de los métodos DNN para procesar data fisiológica. En otras palabras, con un conjunto de datos suficientemente grande y con la complejidad adecuada, puede extraerse información importante de la data, mientras se descartan el ruido y los artefactos.
También puede notarse en la Tabla 2 y en la Tabla 3 que el MdAE por sí mismo no mide un buen resultado. Además, al tener un MdAE bajo los resultados presentan un RMSE considerable, ya que se refuerza la alta variación de los resultados y el cálculo de la mediana no toma en cuenta lo mucho que se desvían los resultados extremos del valor deseado, solo se calculan los valores en el centro. Esto puede observarseen el gráfico de dispersión entre las predicciones y los valores verdaderos presentados en la Figura 4 y en la Figura 5.
Para comparar mejor el desempeño de nuestro método contra la literatura revisada, la Tabla 4 presenta un resumen de los resultados de cada método. El mejor resultado en el conjunto de datos CapnoBase obtenido por el método propuesto por Khreis et al. [16], que alcanzó un MdAE de 0,2 respiraciones/min, mientras que los métodos de referencia previos obtuvieron uno de 0,8 respiraciones/min en el mismo conjunto de datos (excluyendo de la data el 36 % más ruidoso). El método desarrollado alcanzó un MdAE de 1,2 respiraciones/min utilizando la data completa.
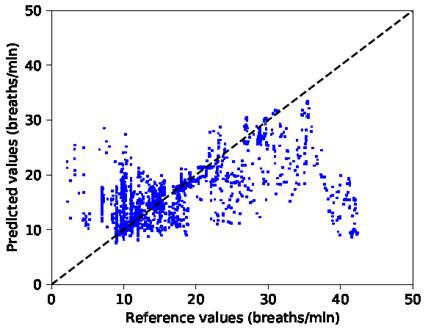
Figura 4. Dispersión de las predicciones y los valores verdaderos de la RR en el conjunto de datos CapnoBase. Las muestras graficadas tienen un SQI por encima de 0.9
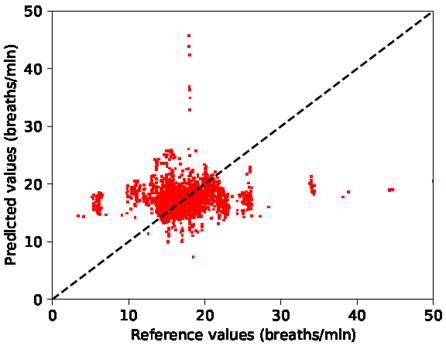
Figura 5. Dispersión de las predicciones y los valores verdaderos de la RR en el conjunto de datos BIDMC. Las muestras graficadas tienen un SQI por encima de 0,9
La base de datos BIDMC parece más desafiante, dado que los métodos probados sobre este conjunto de datos mostraron un MdAE mínimo de 2,3 respiraciones/min, y nuestro método alcanzó un MdAE de 1,5 respiraciones/min. Khreis et al. [16] no utilizaron el conjunto de datos BIDMC en su estudio, por lo que no fue posible comparar los resultados con su método sobre este conjunto de datos.
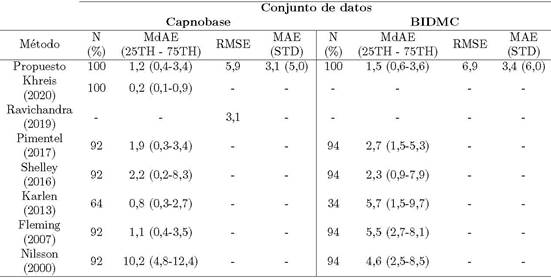
Tabla 4. Medidas de error de diferentes métodos presentados en la literatura. Se incluye N, que es el porcentaje de ventanas PPG utilizadas, el error absoluto mediano (Median Absolute Error, MdAE) y sus percentiles 25avo y 75avo, la raíz cuadrada del error cuadrático medio (Root Mean Squared Error, RMSE) y error absoluto medio (Mean Absolute Error, MAE) y su desviación estándar (standard deviation, STD)
4. Conclusiones
Este trabajo presenta una metodología para utilizar un enfoque DNN para estimar la RR utilizando señales PPG. El modelo se inspiró en una arquitectura exitosa previa, que fue optimizada para nuestro problema utilizando una optimización genética adaptada. Las entradas a la DNN son tres señales respiratorias relacionadas con la RR extraídas de la PPG, y la salida es el valor de RR correspondiente. Para probar la metodología, los archivos de dos conjuntos de datos de acceso abierto se dividieron en cuatro grupos, manteniendo la misma proporción de los archivos de cada conjunto de datos en cada grupo. Se repitió cuatro veces un procedimiento de entrenamiento-prueba, cada uno con tres grupos para entrenar y uno para probar, por lo que cada grupo se utilizó una vez como prueba. Los resultados alcanzados son comparables con la mayoría de las metodologías analíticas de referencia (benchmark) utilizando el conjunto de datos CapnoBase, y la DNN los superó en el conjunto de datos BIDMC, que es más desafiante, mostrando el éxito de la metodología para procesar data fisiológica.
Aunque exitoso, usualmente, el desempeño de los métodos analíticos se acompaña por umbrales heurísticos o un número grande de parámetros libres entonados por un experto, los cuales pueden impedir la generalización de las metodologías desarrolladas. Sin embargo, los enfoques DNN están diseñados para generalizar la data lo mayor posible y tener tan poco preprocesamiento como sea posible.