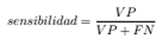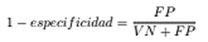Forma sugerida de citación: Torres-Vásquez, M.; Hernández-Torruco, J.; Hernández-Ocaña, B. y Chávez-Bosquez, O. (2021). «Impacto de los algoritmos de sobremuestreo en la clasificación de subtipos principales del Síndrome de Guillain-Barré». Ingenius. N.° 25, (enero-junio). pp. 20-31. doi: https://doi.org/10.17163/ings.n25.2021.02.
1. Introducción
El síndrome de Guillain-Barré (SGB) se define como una polirradiculoneuropatía autoinmune y es la causa más frecuente de parálisis generalizada aguda [1]. El SGB ocurre cuando el sistema inmunitario ataca parte del sistema nervioso periférico. Esta enfermedad es de rápida evolución y es caracterizada con debilidad en las piernas avanzando hacia los brazos, «parálisis ascendente». Los primeros síntomas son debilidad muscular y hormigueo en las extremidades. Los casos graves requieren de ventilación mecánica. Se desconoce la causa, sin embargo, dos tercios de los casos anteceden a una infección respiratoria o gastroenteritis aguda. Recientemente se ha asociado al virus del Zika. El SGB afecta entre 0.4 y 2.4 casos por 100,000 habitantes/año. Se presenta a cualquier edad, sin embargo, suele tener mayor frecuencia en personas de entre 50 y 80 años. Es ligeramente más frecuente en el hombre que en la mujer. Tiene una tasa de mortalidad de entre 2 y 8 %. La mayoría de las personas eventualmente se recuperan completamente cuando la afección es ligera o moderada, en otros casos pueden quedar con daños en el sistema nervioso por mucho tiempo o incluso en forma permanente [2]. Los estudios electrofisiológicos y de conducción nerviosa determinan las pruebas para el diagnóstico de SGB. Existen cuatro subtipos principales de SGB:
-
• Polineuropatía desmielinizante inflamatoria aguda (AIDP).
• Neuropatía axonal motora aguda (AMAN).
• Neuropatía axonal sensorial aguda (AMSAN).
• Síndrome de Miller-Fisher (MF).
La recuperación del paciente depende en gran medida de la pronta identificación del subtipo de SGB. Cada subtipo debe tratarse de manera diferente, el tratamiento y los costos varían según el subtipo desarrollado por el paciente. En los casos graves que generan inmovilidad transitoria o permanente, las terapias de rehabilitación suelen ser tardadas y costosas generando repercusiones psicológicas y económicas al enfermo y a los familiares.
El aprendizaje Automático o Machine Learning es una rama de la Inteligencia Artificial que utiliza diversas técnicas matemáticas, estadísticas, y de optimización, con el objetivo de desarrollar herramientas de análisis de información para que las computadoras «aprendan» a través de ejemplos [3]. En la actualidad disciplinas como finanzas, petróleo, mercadeo, ventas y salud utilizan el aprendizaje automático como herramienta tecnológica para hacer predicciones. Específicamente en el área de la salud se desarrollan cada vez más modelos para el diagnóstico de enfermedades como son el cáncer [4], [5], diabetes [6], [7], Parkinson [8] y Alzheimer [9] dando excelentes resultados.
Los algoritmos de clasificación son los encargados de analizar los datos proporcionados y determinan los pacientes que están sanos y los que se encuentran enfermos. Sin embargo, uno de los problemas más comunes en el diagnóstico médico es la desproporcionalidad de casos. En la vida real existen más casos de pacientes sanos que de pacientes enfermos. Por ejemplo, si queremos diagnosticar pacientes con diabetes, encontramos que un mayor número de gente está sana y un menor número padece diabetes. A esta desproporción de datos se le llama desbalanceo de datos. Existen dos tipos de desbalanceo: desbalanceo binario y desbalanceo multiclase. El desbalanceo binario se presenta cuando en un conjunto de datos formado por dos clases, una tiene un mayor número de datos (clase mayoritaria) respecto a la otra (clase minoritaria). Por otro lado, el desbalanceo multiclase se presenta cuando un conjunto de datos lo forman más de dos clases y su distribución de datos es desigual para cada una de las clases [10].
El desbalanceo de datos puede afectar el resultado de los clasificadores ya que tienden a sesgar sus resultados hacia la clase mayoritaria (pacientes sanos). Los algoritmos de clasificación estándar están construidos para datos balanceados, es decir, el mismo número de casos sanos y casos enfermos. Por ejemplo, para el caso de los pacientes con diabetes, el clasificador ignorará los pacientes con diabetes y solo tomará en cuenta los pacientes sanos. El problema es que queremos determinar los pacientes enfermos y no los pacientes sanos. Es por eso que es necesario utilizar técnicas que ayuden a balancear los datos. En la literatura especializada existen tres técnicas más comunes para resolver el problema del desbalanceo de datos [11].
-
• Nivel de datos. Esta técnica agrega o elimina datos a la clase hasta equilibrar el dataset. Esta técnica también se le conoce como de muestreo y está dividida en tres grupos:
-
– Sobremuestreo: consiste en agregar datos a la clase minoritaria hasta lograr el equilibrio con la clase mayoritaria.
– Submuestreo: consiste en eliminar datos de la clase mayoritaria hasta alcanzar el equilibrio con la clase minoritaria.
– Híbridos: esta técnica combina el sobremuestreo y el submuestreo al mismo tiempo para lograr un mejor equilibrio entre clases.
• Nivel algoritmo. Adaptan o crean algoritmos de clasificación para reforzar la predicción de la clase.
• Costo sensitivo. Consideran los costos asociados con clasificación errónea de las muestras. Utiliza diferentes matrices de costo que describen los costos de clasificar erróneamente cualquier ejemplo de datos en particular.
-
La técnica a nivel de datos es una de las más utilizadas ya que es independiente del clasificador que se utiliza; además, los datos son tratados antes de ser utilizados por el clasificador. La técnica de sobremuestreo es la más empleada ya que agrega datos a la clase minoritaria. Existen diferentes técnicas de sobremuestreo que generan datos dando buenos resultados respecto al submuestreo que puede llegar a eliminar datos de importancia y afectar el resultado del clasificador [12].
Por otro lado, además del desbalanceo de los datos, la distribución de las instancias afecta el resultado de los clasificadores [13]. Existen técnicas que agregan datos sintéticos a la clase minoritaria y las colocan en lugares estratégicos para solventar el problema del desbalanceo y la posición de las instancias.
El objetivo de este estudio fue doble. El primero fue identificar cuál de los tres algoritmos de sobremuestreo utilizados para balancear el dataset de SGB original mejora el resultado de los algoritmos de clasificación. El segundo objetivo fue establecer si balancear los datos mejora el rendimiento de los modelos predictivos creados con datos balanceados, respecto a los modelos creados con datos desbalanceados. Para esto, utilizamos la prueba estadística Wilcoxon para conocer si existe diferencia estadísticamente significativa entre dichos modelos. Actualmente, no existe en la literatura especializada estudios para identificar los subtipos principales de SGB utilizando algoritmos de aprendizaje automático. En previos estudios [14], [15], se crearon modelos predictivos utilizando el dataset original desbalanceado. En este estudio experimental, balanceamos los subsets de entrenamiento utilizando tres técnicas de sobremuestreo (ROS, SMOTE y ADASYN). Los resultados demuestran que balancear los datos mejoran el rendimiento de los modelos predictivos. En algunos casos se logró un rendimiento de 90 %.
Para este estudio, primero utilizamos dos técnicas de binarización (OVO y OVA) para crear diez subsets binarios. Después dividimos los subsets en sets de entrenamiento con un 66 % de los datos y sets de prueba con un 33 % de los datos. Una vez obtenidos los datos de entrenamiento, se les aplicaron tres métodos de balanceo (ROS, SMOTE y ADASYN), para sobremuestrear la clase minoritaria y equilibrarla con la clase mayoritaria. Una vez balanceado los datos se aplicaron tres algoritmos de clasificación con diferentes enfoques: C4.5 (árbol de decisión), SVM (Support Vector Machine), JRip (Ripper). El rendimiento de los modelos predictivos se determinó utilizando el área bajo la curva (AUC) de la curva ROC. Los resultados de los modelos predictivos son el promedio del AUC de 60 ejecuciones. Finalizamos aplicando la prueba Wilcoxon a los modelos creados con datos balanceados que superaron el rendimiento de los modelos creados con los datos desbalanceados, para conocer si existe diferencia estadísticamente significativa entre dichos modelos.
2. Materiales y métodos
2.1. Dataset
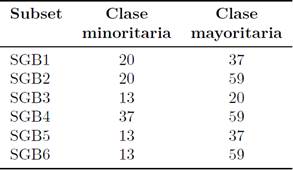
El dataset utilizado en este estudio es una recopilación de 129 pacientes diagnosticados con SGB. A cada uno de los pacientes se les identificó con alguno de los cuatro subtipos principales de SGB. En la Tabla 1 se muestran las características principales del dataset.
Esta información se obtuvo a través del Instituto Nacional de Neurología y Neurocirugía de la Ciudad de México. El dataset original consta de 356 variables. En un artículo anterior se identificaron 16 variables como las más relevantes [16]. Las primeras 4 variables son de tipo clínico, las siguientes 14 variables pertenecen a la prueba de conducción nerviosa. A continuación se muestran las variables utilizadas en los experimentos:
v22: Simetría (en debilidad)
v29: Afectación de los músculos extraoculares
v30: Ptosis
v31: Implicación cerebelosa
v63: Amplitud del nervio motor mediano izquierdo
v106: Área bajo la curva del nervio motor cubital izquierdo
v120: Área bajo la curva del nervio motor cubital derecho
v130: Amplitud del nervio motor tibial izquierdo
v141: Amplitud del nervio motor tibial derecho
v161: Área bajo la curva del nervio motor peroneo derecho
v172: Amplitud del nervio sensorial mediano izquierdo
v177: Amplitud del nervio sensorial mediano derecho
v178: Área bajo la curva del nervio sensorial mediano derecho
v186: Latencia del nervio sensorial cubital derecho
v187: Amplitud del nervio sensorial cubital derecho
v198: Área bajo la curva del nervio sensorial sural derecho
2.2. Algoritmos de aprendizaje automático
2.2.1. Algoritmos de sobremuestreo
Los algoritmos de sobremuestreo son una técnica a nivel de datos que agregan datos a la clase minoritaria con el objetivo de equilibrar el conjunto desbalanceado de datos. Existen diversos algoritmos para sobremuestrear las clases. Para este estudio utilizamos tres técnicas que generan instancias con diferentes enfoques:
1. El algoritmo de sobremuestreo aleatorio ROS (Random Oversampling), obtiene una muestra al azar de instancias de la clase minoritaria y realiza una copia de ellas. Las instancias duplicadas se colocan en forma aleatoria dentro del dataset. ROS es un método no heurístico que tiene como objetivo balancear la clase minoritaria con la mayoritaria [17].
2. El algoritmo de sobremuestro sintético SMOTE (Synthetic Minority Oversampling Technique) sobremuestrea la clase minoritaria generando instancias sintéticas con el objetivo de equilibrarla con la mayoritaria [18]. Las nuevas instancias sintéticas se generan a través de la interpolación entre varias instancias de clases minoritarias basándose en la regla del vecino más cercano. SMOTE realiza este procedimiento en el «espacio de características». El procedimiento para generar los datos sintéticos es el siguiente: (a) Se determina el porcentaje de sobremuestreo que se necesita generar. (b) Para generar los objetos sintéticos realiza el siguiente proceso: (b1) Selecciona una instancia de clase minoritaria al azar. (b2) Elige aleatoriamente sus k-vecinos más cercanos de acuerdo con la distancia euclidiana. (b3) Se toma la diferencia entre el vector de características y cada uno de los vecinos seleccionados. (b4) Esta diferencia se multiplica por un número aleatorio 0y 1. (b5) Suma este último valor al valor original de la muestra. (b6) Devuelve la muestra sintética.(c) La nueva muestra sintética se colocará entre la instancia seleccionada originalmente y cada uno de los k-vecinos más cercanos.
La diferencia principal entre SMOTE y ROS esque ROS duplica datos de la clase minoritariay las agrega en forma aleatoria. SMOTE generadatos sintéticos y los ubica en un vecindario dela clase minoritaria.
3. El algoritmo de enfoque de muestreo sintético adaptativo llamado ADASYN, (Adaptive Synthetic Sampling Approach for Imbalanced Learning), es una extensión de SMOTE. ADASYN tiene dos objetivos: el primero es crear instancias sintéticas a través de la interpolación lineal, entre las instancias de la clase minoritaria para reducir su desequilibrio con la clase mayoritaria del dataset. El segundo objetivo que hace diferente a ADASYN respecto a SMOTE es que los datos generados cambian adaptivamente el límite de decisión agregando datos en la zona de la clase minoritaria difícil de aprender en comparación de los datos de la clase minoritaria fáciles de aprender, esto a través de una distribución de densidad. ADASYN busca darle mayor peso a los datos de la clase minoritaria que son difíciles de aprender [19].
2.2.2. Algoritmos de clasificación
Utilizamos tres algoritmos de clasificación que determinan sus resultados a través de diferentes enfoques. El objetivo es contrastar los resultados de cada uno de ellos:
1. Árbol de decisión (C4.5). Es un algoritmo de aprendizaje supervisado en el que cada nodo de rama representa una elección entre varias opciones y cada nodo de hoja representa una decisión. La técnica de clasificación la realiza mediante criterios de división, con una estructura de árbol invertido, similar a un diagrama de flujo. Maneja características continuas y discretas. Tiene alta precisión, estabilidad, es rápido, fácil de interpretar y robusto al ruido. C4.5 basa sus resultados en forma jerárquica y de aprendizaje inductivo, es decir, en el descubrimientode patrones a partir de ejemplos [20].
2. Máquina de vector soporte (SVM): Es un algoritmo de aprendizaje supervisado que se emplea para clasificación binaria. Pertenece a la familia de clasificadores lineales, esto es, mediante una función matemática los datos originales se redimensionan para buscar una separabilidad lineal de los mismos. SVM se basa en el concepto de construir un hiperplano óptimo, es decir, crea una recta que separa a las clases. El objetivo es encontrar el mejor hiperplano que divida mejor el conjunto de datos y maximice el margen entre las clases [21].
3. Ripper (JRip). Es uno de los algoritmos más populares para problemas de clasificación, con un enfoque basado en reglas. Las clases se examinan en tamaño creciente y se genera un conjunto inicial de reglas para la clase usando el error incremental reducido JRip (RIPPER). Procede tratando todos los ejemplos de un juicio particular en los datos de entrenamiento como una clase, y encontrando un conjunto de reglas que cubrir a todos los miembros de esa clase. Posteriormente, pasa a la siguiente clase y hace lo mismo, repitiendo esto hasta que se hayan cubierto todas las clases [22].
2.3. Medida de rendimiento
Evaluamos el rendimiento de los algoritmos de clasificación utilizando el gráfico de características operativas del receptor o curva ROC (Receiver Operating Characteristic) y el área bajo la curva AUC (area under the curve). La curva ROC mide qué tan bien se clasifican las predicciones, así como la calidad de las predicciones del modelo [23]. La curva ROC se define como la sensibilidad, que es la tasa de verdaderos positivos que se muestra en la Ecuación 1. La 1-especificidad es la tasa de falsos positivos, se muestra en la Ecuación 2. Para este experimento, nos sirve para identificar entre uno de los subtipo de SGB.
El área bajo la curva AUC nos permite identificar una clase. Por ejemplo, reconocer si un paciente padece cierta enfermedad o está sano. En esta medida de rendimiento, los valores ≥ .900 se consideran modelos excelentes. Los valores ≥ .700 significa que son buenos modelos. Sin embargo, los valores con ≤ .500 están considerados malos modelos.
2.4. Técnicas de binarización
En problemas de clasificación es común encontrar datasets que están formados por más de dos clases, a esto se le llama dataset multiclase. Algunos algoritmos de clasificación solo pueden ser capaces de discriminar entre dos clases. Es por eso que es común convertir un problema multiclase en subproblemas binarios. En la literatura encontramos dos técnicas de binarización utilizadas: uno contra uno (OVO) y uno contra todos (OVA) por sus siglas en inglés [24].
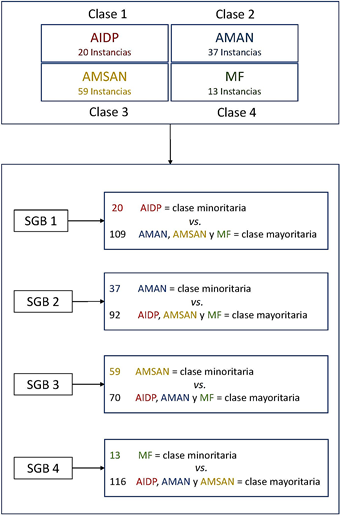
La técnica OVO divide un problema de n clases en n(n − 1)/2 subproblemas binarios, formando todos los posibles pares de clases. La técnica OVA toma una clase como clase minoritaria, las demás clases son combinadas para formar la clase mayoritaria. Este procedimiento se realiza n veces según el número de clases que forman el dataset. Utilizamos las técnicas de binarización OVO y OVA para discriminar una clase de las otras. En problemas de diagnóstico médico sirve para identificar un paciente enfermo de otros pacientes sanos. En las Figuras 1 y 2 mostramos los 4 subsets obtenidos con la técnica OVA y los 6 subsets obtenidos con 1-especificidad OVO al dataset original SGB.
2.5. Validación
Validamos el modelo para cada clasificación utilizando la evaluación train-test. Dividimos el dataset en dos subconjuntos de datos. El primero son los datos de entrenamiento, estos se usaron para construir el modelo. El segundo son llamados datos de prueba, estos se mantienen aparte y a través de ellos se evaluó el modelo. Empleamos 2/3 del conjunto de datos para el entrenamiento y 1/3 del conjunto de datos para las pruebas del modelo.
3. Procedimiento experimental
Como primer paso, tomamos nuestro dataset original desbalanceado multiclase y lo convertimos en dos subproblemas binarios. Utilizamos dos técnicas diferentes de binarización (OVO y OVA). La diferencia entre ellas, es que la técnica OVO crea todas las posibles combinaciones que se pueden formar con las n clases que forman un dataset. Por otro lado, la técnica OVA toma una clase para convertirla en clase minoritaria y las clases restantes son combinadas para formar la clase mayoritaria. OVA crea subconjuntos dependiendo del total de clases que forman el dataset original. El objetivo de crear subsets binarios es que los métodos de balanceo utilizados en este estudio solo identifican dos clases, la clase minoritaria que se sobremuestrea hasta equilibrarla con la mayoritaria.
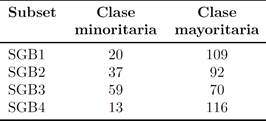
Aplicando las dos técnicas de binarización obtuvimos un total de 10 datasets binarios. En la Tabla 2 se muestran los 4 dataset creados con la técnica OVA y en la Tabla 3 se muestran los 6 dataset binarios creados con la técnica OVO. En la primera columna se muestran los subsets obtenidos con la técnica de binarización. En la segunda columna se observa el número de instancias que forman la clase minoritaria. La tercera columna muestra el número de instancias que integran la clase mayoritaria. Podemos observarque la técnica OVA tiene un mayor desbalanceo dedatos entre la clase minoritaria y la clase mayoritariarespecto a la técnica OVO.
Como segundo paso, dividimos cada uno de los 10 subsets. Fraccionamos los datos en 2/3 para datos de entrenamiento y 1/3 de los datos se utilizaron como datos de prueba. A continuación, se aplicaron los tres algoritmos de sobremuestreo (ROS, SMOTE y ADASYN) a la clase minoritaria que pertenecen a los datos de entrenamiento, hasta equilibrarla con la clase mayoritaria. Los datos de prueba se utilizaron para medir el rendimiento de los modelos obtenidos.
En la Tabla 4 se muestran los 4 subsets balanceados para la técnica OVA. En la Tabla 5 se muestran los 6 subsets balanceados para la técnica OVO. En la primera columna se muestran los subsets de la técnica de binarización. En la segunda columna se muestra la clase minoritaria con el número de instancias que la integran. En la tercera columna se observa el número de instancias que fueron generadas por cada algoritmo de sobremuestreo. Las columnas 4 y 5 muestran la clase minoritaria y la clase mayoritaria balanceadas respectivamente.
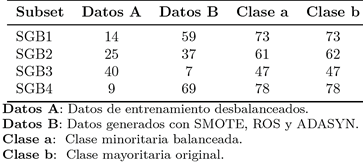
Tabla 4. Resultados de los subsets balanceados aplicando los métodos de sobremuestreo a la clase minoritaria para OVA.
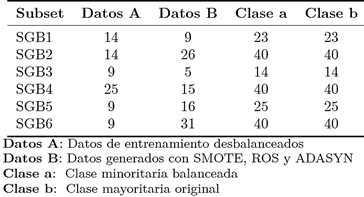
Tabla 5. Resultados de los subsets balanceados aplicando los métodos de sobremuestreo a la clase minoritaria para OVO.
El siguiente paso fue obtener los modelos predictivos aplicando tres algoritmos de clasificación (C4.5, SVM y JRip) a los 10 subsets balanceados. Realizamos 60 ejecuciones independientes calculando el área bajo la curva (AUC) para los 10 subsets. Los modelos predictivos son el resultado del promedio del área bajo la curva de las 60 ejecuciones. Por otro lado, se ejecuta el mismo procedimiento utilizando los subsets desbalanceados para obtener modelos predictivos con datos desbalanceados.
El último paso fue comparar el rendimiento de los modelos obtenidos con datos balanceados contra los obtenidos con los datos desbalanceados. Utilizamos la prueba estadística de Wilcoxon para conocer si existe una diferencia estadísticamente significativa entre los modelos, siempre y cuando los modelos balanceados hayan superado a los desbalanceados. Se utiliza un valor de significación de 0.05.
Los experimentos se realizaron en el software R, diseñado para el análisis estadístico. Se utilizó el entorno de desarrollo integrado RStudio versión 1.2.1335. Los paquetes que utilizamos para balancear los datos fueron: el paquete unbalanced para el algoritmo ROS [25], el paquete DMwR para el algoritmo SMOTE [26] y el paquete UBL para el algoritmo ADASYN [27]. Para los algoritmos de clasificación C4.5 y JRip utilizamos el paquete RWeka 0.4-39 [28]. Para el clasificador SVM usamos el paquete e1071 1.7-0 [29].
El clasificador SVM lineal se optimizó a través de la función tune, asignando los valores; 0.001, 0.01, 0.1, 1, 10, 50, 80, 100 para el parámetro C. Los clasificadores JRip y C45 no requieren optimización de hiperparametros.
4. Resultados y discusión
En las Tablas 6, 7, 8 y 9 se muestran los resultados de los modelos predictivos obtenidos. Aplicamos tres métodos de balanceo (ROS, SMOTE y ADASYN). Sobremuestreamos seis subsets desbalanceados obtenidos con la técnica de binarización OVO y cuatro subsets obtenidos con la técnica de binarización OVA. Cada valor, es el promedio de los resultados obtenidos a través de 60ejecuciones. Se aplican los clasificadores C4.5, SVM y JRip una vez balanceado el conjunto de entrenamiento. Los modelos fueron evaluados utilizando la métrica ROC. Se ejecutó la prueba estadística Wilcoxon a los modelos balanceados contra los desbalanceados, cuando el rendimiento de los modelos balanceados superó el rendimiento de los desbalanceados con el objetivo de conocer si el rendimiento del primero obtenía una diferencia estadísticamente significativa.
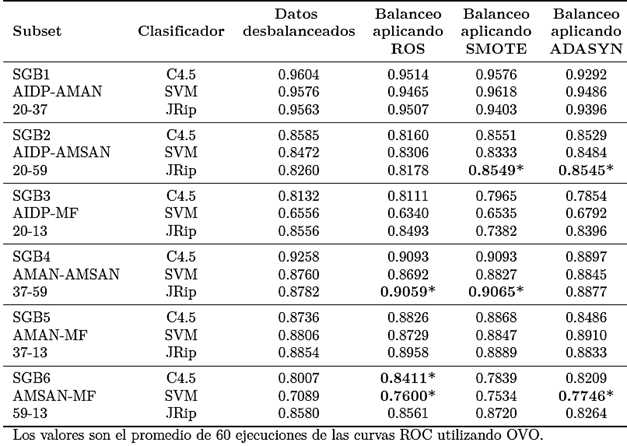
Tabla 6. Tabla de resultados de los modelos predictivos aplicando ROS, SMOTE y ADASYN para sobremuestrear la clase minoritaria.
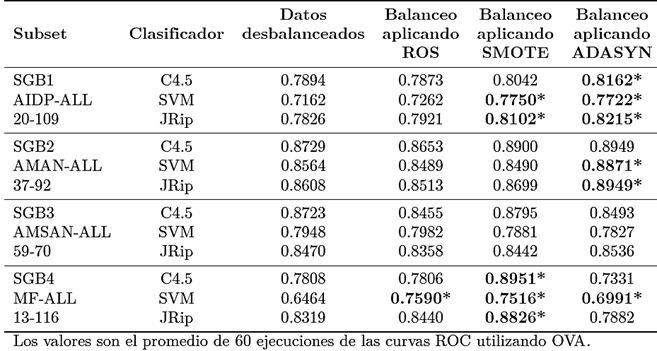
Tabla 9. Tabla de resultados de los modelos predictivos aplicando ROS, SMOTE y ADASYN para sobremuestrear la clase minoritaria.
La estructura de las tablas es la siguiente: la primera columna muestra los subsets obtenidos mediante las técnicas de binarización OVO y OVA, los subtipos de SGB que lo forman, así como la cantidad de instancias para cada subtipo. La segunda columna muestra los tres clasificadores utilizados para obtener los modelos predictivos en cada subset. La tercera columna muestra los resultados de los modelos predictivos utilizando datos desbalanceados. Las columnas 4, 5 y 6 muestran los modelos obtenidos utilizando datos balanceados aplicando tres técnicas de sobremuestreo (ROS, SMOTE y ADASYN). También se observa que, los valores en negrita son los modelos predictivos que, además de superar a los modelos desbalanceados, obtuvieron una diferencia estadísticamente significativa.
En la Tabla 6 se muestran los resultados de los 72 modelos predictivos obtenidos utilizando la técnica de binarización OVO. De estos modelos, 18 fueron creados con datos desbalanceados y 54 se obtuvieron utilizando datos balanceados aplicando tres métodos de sobremuestreo. Se encontraron que 32 modelos balanceados no pudieron superar el rendimiento de los modelos desbalanceados. Otros 15 modelos balanceados superaron el rendimiento de los datos desbalanceados, sin embargo, no se encontró diferencia estadísticamente significativa. Por otro lado, 7 modelos balanceados superaron a los modelos desbalanceados y además tuvieron una diferencia estadísticamente significativa.
Con el subset SGB6 se encontraron los mejores resultados, al obtener 3 modelos con diferencia estadísticamente significativa. Por otro lado, en los subsets SGB2 y SGB4 tuvieron 2 modelos con diferencia estadísticamente significativa cada uno. Los subsetsSGB1, SGB3 y SGB5 obtuvieron el peor rendimiento respecto a los modelos desbalanceados ya que en ninguno de los modelos se encontró diferencia estadísticamente significativa.
Respecto a los métodos de balanceo, en la Tabla 7 se muestran los resultados del ranking obtenido por cada método. Estos resultados se obtuvieron al asignar una posición a cada método dependiendo de su rendimiento con cada subset. Por cada fila, se asigna un valor a cada método de sobremuestreo. En la primera fila, a SMOTE se le asigna el valor 1 ya que obtuvo el mejor rendimiento. A ROS se le asigna el valor 2 ya que obtuvo el siguiente rendimiento y finalmente a ADASYN se le asigna el valor 3 ya que fue el método con el peor rendimiento. Esta operación se realiza para cada fila. Seguidamente, se suman todos los valores por cada método y se dividen por el número de filas para obtener el promedio. Por ejemplo, SMOTE obtuvo 5 veces el primer lugar, 6 veces el segundo lugar, 5 veces el tercer lugar y 2 veces el cuarto lugar. La suma de estos valores es de 40 y se divide por el número de filas de la tabla, para este caso es 18. El resultado es 2.222 y al ser el promedio más bajo, ocupa el número 1 en el ranking [30].
Para OVO, el algoritmo SMOTE fue el método de balanceo con el mejor rendimiento con una puntuación promedio de 2.2222. Los algoritmos ADASYN y ROS, ocuparon el segundo lugar al obtener la misma puntuación promedio de 2.7222. Respecto a los clasificadores, en la Tabla 8 se muestra que el clasificador JRip, obtuvo el mejor rendimiento con una puntuación promedio de 1.6667. El clasificador C4.5 obtuvo el segundo lugar con una puntuación promedio de 1.8333. Por último, el clasificador SVM obtuvo el peor rendimiento con una puntuación promedio de 2.500.
En la Tabla 9 se muestran los resultados de 48 modelos predictivos, obtenidos utilizando la técnica de binarización OVA. De estos, 12 modelos fueron creados con datos desbalanceados y 36 modelos se obtuvieron utilizando datos balanceados aplicando tres métodos de sobremuestreo. Se encontró que 15 modelos balanceados no pudieron superar el rendimiento de los modelos desbalanceados. En 9 modelos balanceados superaron el rendimiento de los datos desbalanceados, sin embargo, no se encontró diferencia estadísticamente significativa. Por otro lado, 12 modelos balanceados superaron a los datos desbalanceados y, además, tuvieron una diferencia estadísticamente significativa.
Con los subsets SGB1 y SGB4 obtuvieron los mejores rendimientos. En el subset SGB1, 8 modelos balanceados mejoraron los modelos desbalanceados, de los cuales, 5 obtuvieron diferencia estadísticamente significativa. En el subset SGB4, 6 modelos balanceados superaron los datos desbalanceados, de estos, 5 modelos obtuvieron diferencia estadísticamente significativa. Con el subset SGB2, 5 modelos balanceados superaron a los modelos desbalanceados, sin embargo, solo 2 modelos obtuvieron diferencia estadísticamente significativa. En el subset SGB3 obtuvo el peor rendimiento. Solo 3 modelos balanceados superaron los datos desbalanceados, sin encontrar diferencia estadísticamente significativa.
En la Tabla 10 se muestran los resultados del ranking para los métodos de balanceo aplicando la técnica de binarización OVA. El algoritmo SMOTE obtuvo el mejor rendimiento con una puntuación promedio de 1.9167. El algoritmo ADASYN obtuvo el segundo lugar con una puntuación promedio de 2.1667. Por último, ROS fue el algoritmo de balanceo con el peor rendimiento, ubicándolo en el tercer lugar con una puntación promedio de 3.0833.
Respecto a los clasificadores, en la Tabla 11 se observan los resultados del ranking. El clasificador C4.5 obtuvo el primer lugar con una puntuación promedio de 1.2500. El clasificador JRip ocupa el segundo lugar con una puntuación promedio de 1.500. El tercer puesto lo obtuvo el clasificador SVM, con una puntuación promedio de 2.7500.
La técnica de binarización OVA fue la que obtuvo los mejores resultados. Se obtuvieron 36 modelos predictivos con datos balanceados. De estos, 12 modelos predictivos obtuvieron diferencia estadísticamente significativa. El algoritmo SMOTE fue el método de balanceo con los mejores resultados. El clasificador JRip fue de acuerdo al ranking el mejor algoritmo.
La técnica de binarización OVO obtuvo el peor rendimiento. Se obtuvieron 54 modelos predictivos con datos balanceados, de estos, 7 modelos predictivos lograron obtener diferencia estadísticamente significativa. El algoritmo ADASYN, obtuvo el mejor rendimiento como método de sobremuestreo. El clasificador C4.5 alcanzó el mejor rendimiento al obtener la menor puntuación promedio.
5. Conclusiones
En esta investigación, realizamos una exploración de tres algoritmos de sobremuestreo (ROS, SMOTE y ADASYN), con el objetivo de conocer cuál obtiene el mejor rendimiento; además, conocer si balancear el dataset original mejora el rendimiento de los modelos predictivos realizados con datos desbalanceados. Estos experimentos se realizaron con un dataset real de pacientes diagnosticados con algún subtipo de SGB. Comenzamos creando subsets binarios aplicando dos técnicas (OVO y OVA) al dataset original. Obtuvimos 10 subsets divididos en: 6 subsets con la técnica OVO y 4 subsets con la técnica OVA. Fraccionamos cada subset en entrenamiento con 66 % de los datos y 34 % de los datos como prueba. Sobremuestreamos las clases minoritarias de los subsets de entrenamiento aplicando ROS, SMOTE y ADASYN con la finalidad de equilibrar la clase minoritaria con la clase mayoritaria. Una vez balanceados los subsets aplicamos tres clasificadores: C4.5, JRip y SVM. Los resultados son el promedio de la curva ROC de 60 ejecuciones. Se aplicó la prueba Wilcoxon a los modelos predictivos obtenidos con datos balanceados que superaron el rendimiento de los modelos con datos desbalanceados para conocer si existe diferencia estadísticamente significativa entre ellos.
La técnica de binarización OVA obtuvo el mejor resultado en comparación con la técnica OVO. Aplicando la técnica OVA se obtuvieron 36 modelos predictivos con datos balanceados, de los cuales 12 obtuvieron diferencia estadísticamente significativa. El mejor algoritmo para balancear los datos fue SMOTE respecto a ROS y ADASYN. El algoritmo SMOTE mejoró el rendimiento de los modelos predictivos de acuerdo con sus características de sobremuestreo. SMOTE agrega instancias de la clase minoritaria extrapolando nuevas instancias en lugar de duplicarlas como lo hace el algoritmo ROS. El algoritmo ROS copia instancias de la clase minoritaria y las agrega al azar duplicando información que puede confundir a los clasificadores. Por otro lado, ADASYN es una variante de SMOTE el cual agrega instancias a la clase minoritaria que son difíciles de aprender, especialmente las que se encuentran en el borde de decisión, este enfoque puede no ser suficiente información para que el clasificador identifique las clases y mejore el resultado. El clasificadorC4.5 obtuvo el mejor rendimiento según la puntuación promedio para OVO.
Los resultados demuestran que, balancear los datos mejoran el rendimiento de los modelos predictivos obtenidos con datos desbalanceados. Por otro lado, utilizar algoritmos de aprendizaje automático en problemas de diagnóstico de enfermedades es factible y puede contribuir en la identificación del subtipo de SGB que un paciente contraiga. Como trabajos futuros exploraremos con hibridación de técnicas de sobremuestreo y submuestreo, además de utilizar otros clasificadores.