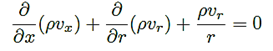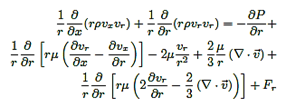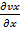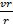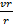1. Introducción
En el campo de la ingeniería, los instrumentos que miden el caudal de un fluido están clasificados en dos clases, los instrumentos mecánicos y los instrumentos de pérdida de carga [1, 2], y se detallan en el texto de la ASME [3]. Entre estos se encuentra el tubo Venturi, como instrumento de pérdida de carga por contracción de vena, el cual fue inventado por Clemans Herschel (1842-1930) [4], y nombrado así en honor de Giovanni Battista Venturi (1746-1822) por sus trabajos pioneros acerca del flujo en secciones cónicas [2].
Los flujos en tales instrumentos, en su mayoría, son turbulentos, y se caracterizan por tener fluctuaciones aleatorias y rápidas de remolinos, los cuales transportan masa, energía, cantidad de movimiento a otras regiones del flujo, donde las fluctuaciones adicionan transferencia de movimiento y de energía, además, están relacionados con valores altos de coeficientes de fricción, transferencia de calor y transferencia de masa [1, 2].
Mediante el número adimensional de Reynolds [5,6] se determina si el flujo es laminar o turbulento, donde el número de Reynolds es el parámetro que expresa la relación entre las fuerzas de inercia y las viscosas en un fluido, siendo la fuerza de inercia el producto de la velocidad promedio y del diámetro interno, y de la fuerza viscosa la viscosidad cinemática. El flujo laminar es considerado para el número de Reynolds con valores menores de 2300, en el rango del número de Reynolds de 2300-4000 el flujo es considerado en transición, y para el número de Reynolds mayores de 4000 el flujo es turbulento, y se tiene una representación gráfica conocido como el diagrama de Moody [1, 2]. Otros estudios realizados sobre superficies acondicionadas reportan que el número de Reynolds tiene valores distintos para flujo laminar y turbulento.
Para reproducir el comportamiento del flujo mediante la dinámica de fluidos computacional (CFD, por su sigla en inglés) [7], se requiere de datos experimentales para su calibración y validación, tales como: la presión, la temperatura, la velocidad, que son parámetros que se pueden medir en laboratorio o en espacios abiertos. Además, la CFD requiere del empleo de un modelo de turbulencia que resuelve el problema de cierre en las ecuaciones promediadas de las ecuaciones generales de Navier-Stokes. De la diversidad de los modelos de turbulencia para el flujo de fluidos, se debe seleccionar los perfiles de las soluciones numéricas que se ajusten más a los resultados experimentales. Una vez evaluado el modelo de turbulencia, es posible continuar el desarrollo de las simulaciones computacionales deseadas para determinar el comportamiento del campo de flujo bajo ciertas consideraciones, sea para un flujo interno o externo. Cabe señalar que, en ciertas regiones críticas, los resultados numéricos evaluados con diferentes modelos de turbulencia [8] son distintos, y en regiones menos críticas los resultados son similares, debido a la capa límite y de la interacción de la separación de flujo [9, 10].
Una investigación experimental fue realizada por Lindley [11] para el tránsito del flujo en un tubo Venturi clásico, donde al inicio de la sección de la garganta, el flujo de agua presentó caídas de presión en una sección de la pared. Posteriormente, para la misma geometría, Sattery y Reader [12] simularon el flujo mediante la CFD, donde en la sección de la garganta los perfiles numéricos mostraron caídas de presión. Un resultado similar de la caída de presión también fue obtenido por Tamhakar et al. [13], aplicando la CFD, para un tubo Venturi de dimensiones diferente. Por lo cual, se ha motivado en continuar con la investigación de la presión del flujo en medidores Venturi.
En el presente trabajo se realiza un estudio experimental y numérico de la presión que ejerce el flujo de agua en las paredes de un tubo Venturi. En el caso experimental se realiza el estudio para cinco experimentos con caudales diferentes, en el caso numérico se realiza el estudio para dos modelos de turbulencia: k–e estándar de Launder y Spalding [14] y k–ω estándar de Wilcox [15], y para dos dominios discretizados por el método de elementos finitos (MEF), una con celdas cuadriláteras y otra con celdas triangulares, con el fin de determinar en qué regiones del flujo se producen las caídas mínimas de la presión. Asimismo, validar los dos modelos de turbulencia empleados con los datos experimentales de presión. Cabe señalar, las presiones experimentales son medidas en puntos específicos que están separados entre sí por una distancia establecida a lo largo de la pared del tubo Venturi, y no aporta información de presiones en secciones críticas; mientras que, los perfiles numéricos son trayectorias continuas y aportan mayor información de la presión a lo largo de toda la pared.
Se presenta el fundamento matemático, se exponen los procedimientos y los resultados de los experimentos y de las simulaciones numéricas. Posteriormente, se presentan las conclusiones del análisis realizado.
2. Materiales y métodos
2.1. Instalación experimental
El tubo Venturi sometido a estudio en el presente trabajo se muestra en la Figura 1. Es un dispositivo fabricado por la empresa TecQuipment, el cual se utiliza en ensayos experimentales para determinar el caudal de agua por diferencia de presión. El equipo experimental se encuentra instalado en el laboratorio de la Sección de Termofluidos del Departamento de Ingeniería Mecánica de la Universidad Nacional Experimental Politécnica “Antonio José de Sucre” Vice-Rectorado Puerto Ordaz, Bolívar, Venezuela. El tubo Venturi consta de cinco secciones: una sección recta, una sección convergente, una sección recta la cual es la garganta, una sección divergente, y otra sección recta. En la imagen, se muestran un total de once mangueras plásticas que son llamadas tubos piezométricos, las cuales sirven para medir las lecturas de alturas piezométricas de las columnas de agua, y están conectados al tubo Venturi y al colector (manifold) de vidrio. En la salida del tubo Venturi está ubicada la válvula de control y, en el extremo derecho del colector la válvula de purga. Antes del tubo Venturi está ubicada la válvula de regulación de caudal y esta se encuentra después de la bomba, la cual no se muestra en la figura.

Figura 1. Equipo experimental tubo Venturi. Las lecturas de las columnas de agua se miden en milímetros.
La geometría 3D y la proyección en el plano del tubo Venturi se ilustran en la Figura 2, donde se muestran las ubicaciones de las referencias A, B, C, D, E, F, G, H, J, K y L, lugar donde se conectan las once mangueras plásticas. La referencia A está ubicado al inicio de la sección recta; B y C están ubicados en la sección convergente; D en la mitad de la sección recta de la garganta; E, F, G, H, J y K ubicados en la sección divergente; y L está ubicado al final de la sección recta, a la salida del tubo Venturi. El diámetro interno mayor de las dos secciones rectas es 26 mm, el diámetro interno de la garganta 16 mm, siendo la longitud total del tubo Venturi de 156 mm. Los diámetros internos de las secciones transversales y de las ubicaciones de las referencias se muestran en la Tabla 1.
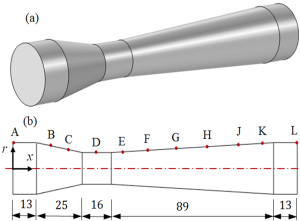
Figura 2. (a) Geometría 3D del tubo Venturi. (b) Ubicación de las referencias y dimensiones de las secciones longitudinales en milímetros.

Tabla 1. Diámetro interno para cada referencia, y distancia axial donde están ubicadas las referencias
El ensayo experimental se realizó mediante los siguientes pasos: inicialmente, se abrieron las dos válvulas al 100 %, la válvula de regulación de caudal y de control de caudal. Una vez que la bomba del banco de prueba estuvo en funcionamiento, la válvula de control se cerró 100 %, se permitió que saliera el aire atrapado en las mangueras y en el colector a través de la válvula de purga y quedando totalmente llena de agua; seguidamente, la válvula de regulación se cerró 100 %. Luego, se abrió la válvula de control 100 %, y por la válvula de purga se permitió el ingreso de aire proveniente de la atmósfera local, para permitir que se formaran las columnas de agua a la altura establecida de 140 mm como posición inicial, todas al mismo nivel, para las once mangueras. La toma de lectura de 140 mm quedó dentro del rango de 0,0–200 mm del panel, tal como se muestra en la Figura 3. Seguidamente, incrementando la abertura de la válvula de regulación se realizaron cinco ensayos experimentales para la toma visual de lecturas piezométricas, para el rango de caudal de 2, 244×10−4 −3, 7×10−4 (m3/s).

Figura 3. Posición inicial de las alturas piezométricas de 140 mm de los niveles de las once columnas de agua. Donde, de izquierda a derecha, el primer tubo piezométrico está conectado en la referencia A de la pared del tubo Venturi, el segundo en la referencia B, así mismo, están ubicados los otros hasta la referencia L (ver Figura 2).
2.2. Simulación numérica
2.2.1. Ecuaciones gobernantes
Las ecuaciones gobernantes aplicadas a la CFD, para un flujo incompresible, en condiciones estacionarias, y simuladas para un dominio computacional 2D con simetría axial, en su forma diferencial se expresan como:
Ecuación de la conservación de la masa.
Ecuación de la conservación de cantidad de movimiento lineal, en la dirección axial.
En la dirección radial.
Donde, los parámetros son: la densidad p, la velocidad axial vx y velocidad radial vr, el radio r, la viscosidad μ, los gradientes de presión 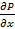 y
y 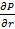 , y las fuerzas en la dirección axial Fx y radial Fr.
, y las fuerzas en la dirección axial Fx y radial Fr.
El modelo de turbulencia va acoplado a la ecuación de cantidad de movimiento lineal, y son ecuaciones de transporte semiempíricas que modelan el mezclado y difusión que se incrementa a causa de remolinos turbulentos, y son resueltas por la ecuación de Navier- Stokes de número de Reynolds promedio (RANS, por sus siglas en inglés) [16]. Las primeras investigaciones de la turbulencia fueron desarrolladas por Kolmogorov (1941) basándose en los resultados de Reynolds (1883). Cabe señalar, para la simulación del flujo en el presente trabajo, se emplean los modelos de turbulencia k – e estándar de Launder y Spalding [14] y k − ω estándar de Wilcox [15].
2.2.2. Dominio computacional y mallado
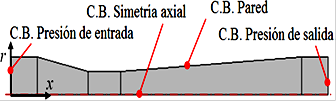
Por la simetría que tiene la geometría del tubo Venturi, se considera el dominio computacional en 2D con simetría axial, la cual se muestra en la Figura 4. Esta simplificación de la geometría de 3D a 2D contribuye en la reducción de la cantidad de celdas de la malla, el tiempo de procesamiento, y el coste computacional del equipo, y es muy común las simplificaciones para sólidos de revolución y geometrías primitivas simétricas. Además, en la misma figura del dominio 2D, se señala donde se aplican las condiciones de borde.
La Figura 5 muestra el dominio mallado 2D, donde el dominio fue mallado para dos tipos de celdas, una cuadrilátera y otra triangular. El dominio mallado con celdas cuadriláteras tiene 19 600 elementos y el dominio mallado con celdas triangulares 18 047 elementos. Para ambos casos, la malla fue refinada en las regiones adyacentes a las paredes, debido a la presencia de esfuerzos cortante en esas regiones del flujo. En la misma figura, se muestra como detalle la sección de la garganta, donde se observa cómo están distribuidas las celdas cuadriláteras y las celdas triangulares.
Como parte de un estudio de convergencia numérica, antes de obtener la malla final que se muestra en la Figura 5, se refinó cinco veces la sección de la garganta hasta obtener una densidad de malla óptima. Dicho refinamiento en la garganta fue por ser una sección crítica por la caída de presión del flujo. En la mitad de la longitud de la garganta, se encuentra ubicado el punto de referencia D (ver Figura 2), allí se obtuvieron los resultados numéricos finales de la presión de 44,79 (mmH2O) para la malla con celdas cuadriláteras y de 51,38 (mmH2O) para las celdas triangulares, evaluados con el modelo de turbulencia k − e estándar; y la presión de 48,53 (mmH2O) para la malla con celdas cuadriláteras y de 55,75 (mmH2O) para las celdas triangulares, evaluados con el modelo de turbulencia k − omega estándar; obteniendo para ambos casos errores numéricos de convergencia numérica menores de 0,01 %.
La calidad de la malla se evaluó para celdas bidimensionales, donde para el caso de las celdas cuadriláteras se obtuvo para el tamaño de elemento máximo de 0,0105 mm y elemento mínimo de 4,68×10 −5 mm, curvatura de 0,3, y tasa de crecimiento de 1,3; asimismo, para el caso de las celdas triangulares se obtuvo para el tamaño de elemento máximo de 3,64×10−4 mm y elemento mínimo de 5,2×10−5mm, curvatura de 0,25, y tasa de crecimiento de 1,15, respectivamente. Dando como resultados finales que los dos dominios mallados con celdas cuadriláteras y triangulares son de buena calidad.
Los dominios computacionales fueron discretizados en la plataforma de mallado del código COMSOL Multiphysics versión 4.3, el cual aplica el método de elementos finitos (MEF).
Las condiciones de borde, para las presiones del flujo de agua aplicadas a la entrada (referencia A) y a la salida (referencia L) del tubo Venturi, se muestran en la Tabla 2.
Las paredes del tubo Venturi se consideran adiabáticas. La velocidad del flujo en la dirección radial y axial en las paredes es nula por la presencia de esfuerzos cortante. En la simetría axial en el eje x, la velocidad del flujo en la dirección radial es nula.
En todo el dominio computacional se considera flujo isotérmico, siendo para la temperatura del agua a 24 °C, la densidad 997,1015 kg⁄m3 y la viscosidad dinámica 0,00091135 Pa.s, donde ambos parámetros físicos son tomados como contantes para la simulación del flujo.

Figura 5. (a) Dominio computacional 2D mallado. Detalle de la sección de la garganta: (b) Malla estructurada con celdas cuadriláteras. (c) Malla con celdas triangulares.
2.2.3. Método de solución computacional y equipo
Para la simulación del flujo isotérmico, en el código COMSOL Multiphysics, se seleccionó la opción geometría 2D con simetría axial y condiciones de flujo estacionario. Para el flujo turbulento se aplicaron los modelos de turbulencia k − e estándar y k − ω estándar, tanto para los dominios mallados con celdas cuadriláteras y triangulares. Para la tolerancia relativa se determinó un valor fijo de 0,001. Para la solución, se estableció la iteración máxima hasta 100, y el método de solución PARDISO (de su acrónimo en inglés, parallel sparse direct solver). Para el procesamiento de datos se utilizó un equipo con las siguientes características: Laptop marca Síragon, modelo M54R, Intel Core 2 Duo, dos procesadores de 1,8 GHz, y memoria RAM de 3 GB.
3. Resultados y discusión
3.1. Resultados experimentales
Los caudales del agua se obtuvieron por el método volumétrico, para cada experimento realizado, y cuyos resultados se muestra en la Tabla 3. Con estos valores de caudales se determinó el número de Reynolds.
En la Tabla 4 se presenta las magnitudes del número de Reynolds obtenidos en la referencia A, L, y D. Donde, en la referencia A, el número de Reynolds tiene la misma magnitud que en la referencia L, esto es porque el tubo Venturi tiene el mismo diámetro. En las referencias A y L, para los cinco experimentos, se obtuvo que el número de Reynolds está en el rango de 12000
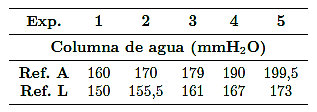
La Tabla 5 muestra los cinco resultados experimentales de alturas piezométricas obtenidos en las referencias A, B, C, D, E, F, G, H, J, K y L, y en la Figura 6 se muestra la gráfica correspondiente de la presión manométrica en (mmH2 O), y la Figura 7 muestra una imagen de las alturas piezométricas de las once columnas de agua correspondiente al experimento 3, y se observa la forma cóncava de los meniscos por efecto de la tensión superficial del agua que se forman en cada columna.
Tomando como referencia de la posición inicial de las once columnas con el nivel de agua a la altura de 140 mm, se observa que, a medida que se incrementa el caudal, el nivel de las columnas del agua en las referencias A y B se incrementan; en la referencia C se mantiene constante; en las referencias D, E y F disminuyen; en la referencia G también se mantiene constante; y, en las referencias H, J, K y L se incrementan. Tomando en cuenta las diferencias de columnas de agua entre A y D, la menor diferencia de presión se tiene para el experimento 1, y la mayor diferencia de presión para el experimento 5. En la misma Figura 6, se observan las pérdidas de presión del fluido en la referencia L, con respecto a la referencia A. De todos los experimentos realizados el que tiene mayor pérdida de presión es el experimento 5.
Para cada experimento, la caída de presión se presenta en la sección de la garganta, tal como se muestra en la referencia D, donde el flujo es inducido a tener una caída de presión de manera forzada, lo cual es conocido como efecto Venturi, y la menor caída de presión se presenta para el experimento 5.

Tabla 5. Datos experimentales de presión manométrica en cada referencia de la pared del tubo Venturi Temperatura del agua: 24 °C
De los resultados obtenidos, en las referencias C que tiene un diámetro interno de 18,4 mm y G que tiene un diámetro de 20,16 mm, por más que se incrementa la velocidad del flujo en esas referencias por el aumento del caudal, las presiones no varían su magnitud confluyendo en un solo lugar para cada referencia mencionada. Esto es consecuencia de que la válvula de control mantiene su abertura de 100 % y el flujo se descarga en un reservorio a la presión de la atmósfera local, y a la vez que la presión del aire atrapado en el colector, que es menor a la presión de la atmósfera local, sostiene la formación de las columnas de agua.
Cabe señalar que, si se mantuviera la válvula reguladora con abertura fija, y se manipulara la válvula de control, no habría intercepción en las referencias C y G, ya que los niveles las columnas de agua se desplazarían hacia arriba o hacia abajo por el incremento o disminución de la presión del flujo en todo el sistema del tubo Venturi.
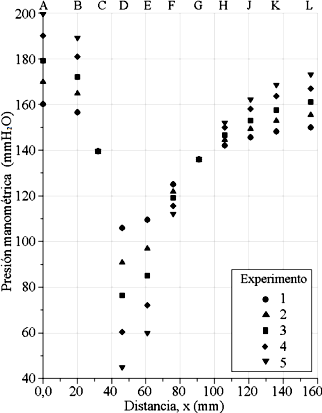
Figura 6. Datos experimentales de lecturas de alturas piezométricas de las columnas de agua tomados en diferentes puntos de referencias de las paredes del tubo Venturi. Temperatura del agua 24 °C.

Figura 7. Alturas piezométricas para diferentes niveles de las columnas de agua, correspondiente al experimento 3.
Por otro lado, si se analiza la pérdida de presión desde la referencia C hasta G, la caída de presión permanece invariable por más que se incremente la energía cinética del fluido en dichas regiones, ya que, como se muestra en la Tabla 5 y graficada en la Figura 6, en la referencia C se tiene una altura piezométrica fija de 139,5 mm y en G de 136,0 mm, donde, la diferencia de presión es de 3,5 (mmH2O), para los cinco experimentos realizados.
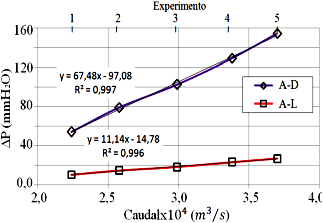
Las diferencias de presión entre las referencias A-D y A-L, se presenta en la Tabla 6, y en la Figura 8 se muestra el comportamiento de ambas rectas mediante la línea de tendencia lineal, para la diferencia de presión de A-D se tienen un valor de coeficiente de determinación R2=0,997, y para la diferencia de presión de A-L un valor de R2=0,996. Ambos resultados muestran que existe una proporcionalidad de diferencia de presión con respecto al caudal.
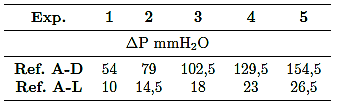
Tabla 6. Diferencia de presión entre la referencia A y D, y la referencia A y L, para cada experimento
Durante el funcionamiento de la bomba, para las tomas de lecturas experimentales, estuvieron presentes las vibraciones en el banco de prueba, por tanto, luego de un tiempo estimado de cuatro a seis minutos, cuando las perturbaciones eran mínimas, se procedieron a tomar las lecturas por observación directa del nivel de cada una de las once columnas de agua en la unidad de medida de un milímetro, y para la toma de lectura del nivel del agua que se ubicaba en el medio de la unidad de milímetro se hizo uso de una lupa para la amplificación de la imagen.
Los resultados experimentales obtenidos no cuantifican la magnitud de la presión entre cada referencia, por tener una distancia de separación, por lo cual, es de interés cuantificar y conocer cómo se comporta de manera continua la trayectoria del perfil de presión a lo largo de las paredes del tubo Venturi, siendo de mayor interés entre las referencias C y E, lugar donde se producen las mayores caídas de presión, para esto, se debe simular el flujo mediante la CFD y así conocer lo que realmente podría suceder.
3.2. Resultados numéricos y comparación con los datos experimentales
La simulación de la distribución de la velocidad del flujo isotérmico en el tubo Venturi se muestra en la Figura 9, en la sección transversal y en el plano, donde el incremento de la velocidad del flujo se produce en la garganta, y la disminución en la sección divergente. En la sección divergente las líneas de contorno de velocidad van adquiriendo un perfil parabólico en dirección al eje x, por el efecto de la capa límite. Donde, la velocidad del flujo en la simetría axial del eje x es máxima y disminuye su magnitud hacia las paredes del tubo Venturi, por lo cual se tiene un gradiente de velocidad en el campo de flujo. Cabe señalar, el dominio del flujo que se muestra en la Figura 9, fue simulado con malla estructurada y celdas cuadriláteras, empleando el modelo de turbulencia k − e estándar; y por ser similares, no se exponen otras figuras de las líneas de contorno de velocidad para los resultados k − ω estándar.
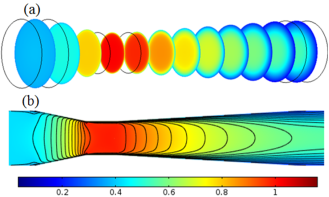
Figura 9. Distribución de velocidad (m⁄s). (a) En la sección transversal, y (b) Proyectado en el plano.
En la Figura 10, se muestra el comportamiento de los perfiles de velocidad evaluados en la simetría axial del eje x. De acuerdo con todas las trayectorias de los perfiles, hacia el final de la sección convergente el flujo incrementa su velocidad, en la sección de la garganta el flujo alcanza una velocidad máxima en la referencia D, y disminuye la velocidad en la sección divergente. Donde, la magnitud de la velocidad del flujo en la referencia A es menor con respecto a la referencia L, por lo cual, se entiende que el comportamiento del perfil de la velocidad del flujo en la dirección radial, en la referencia A tiene menor curvatura y en la referencia L mayor curvatura.
Los resultados numéricos de los caudales se muestran en la Tabla 7, para cada modelo de turbulencia y tipo de mallado. La mayor magnitud de caudal fue para el modelo de turbulencia k−e estándar y dominio mallado con celdas cuadriláteras, y el menor caudal para el modelo de turbulencia k − ω estándar y dominio mallado con celdas triangulares. Acotando que el caudal se determinó con la velocidad promedio del flujo mediante el método de integración numérica.
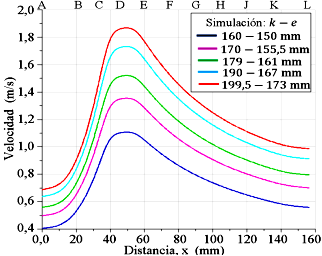
Figura 10. Perfiles de velocidad evaluadas en la simetría axial del eje x, para el modelo de turbulencia k−e estándar.
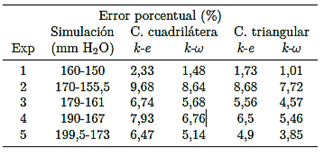
Al comparar los caudales numéricos presentados en la Tabla 7 con los experimentales presentados en la Tabla 3, se tiene que el mayor error porcentual se presentó para el modelo de turbulencia k − e estándar con un error porcentual de 9,68 % para el dominio mallado con celdas cuadriláteras, y de 8,68 % para la malla con celdas triangulares; donde, el mínimo error porcentual fue de 1,48 % para k − e estándar para el mallado con celdas cuadriláteras, y de 1,01 % para k−ω estándar para el mallado con celdas triangulares, tal como se muestra en la Tabla 8. Basándose en los resultados, se evidencia que existe una influencia en los resultados numéricos al aplicar un tipo de mallado al dominio computacional.
Los resultados numéricos de número de Reynolds obtenidos para el diámetro mayor en la referencia A y L se muestra en la Tabla 9, y para el diámetro menor en la referencia D se muestran en la Tabla 10. En la referencia A y L, para las cinco simulaciones, el número de Reynolds se ubicó en el rango de 12100

Tabla 9. Número de Reynolds obtenidos en el diámetro mayor, en la referencia A y L, para dos modelos de turbulencia y dos tipos de mallas aplicadas

Tabla 10. Número de Reynolds obtenidos en el diámetro menor, en la referencia D, para dos modelos de turbulencia y dos tipos de mallas aplicadas
En la Figura 11, se muestran las distribuciones de presiones en la superficie de las paredes de la sección convergente, garganta y divergente, además, la distribución de la presión del flujo interno proyectado en el plano, donde se muestran las líneas de contorno, las cuales son las isóbaras, y se observa de cómo se distribuyen las presiones de forma perpendicular al eje x y hacia las paredes.
Los perfiles de las presiones manométricas obtenidos en las paredes del tubo Venturi se muestran en las Figuras del 12 a l 1 6. Las unidades de las presiones están en milímetros de columna de agua (mmH2O), y en las mismas gráficas están incluidos los datos de las presiones de los experimentos realizados. Los perfiles de las presiones corresponden para un dominio mallado con celdas cuadriláteras y para otro dominio mallado con celdas triangulares, para ambos casos, simulados para flujo isotérmico con el modelo de turbulencia k−e estándar y k − ω estándar.
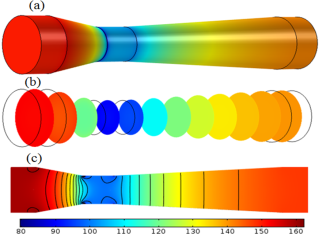
Figura 11 Distribución de presión (mmH2 O). (a) En la superficie de la pared. (b) En la sección transversal, y (c) Proyectado en el plano.
Al observar de forma paralela las Figuras del 12 al 16, todos los perfiles de presiones tienen un comportamiento similar a lo largo de las paredes del tubo Venturi, se interceptan y bordean los datos experimentales. Al final de la sección recta, de la entrada del tubo Venturi, los perfiles muestran un incremento de la presión, incrementando a una magnitud mayor al de la presión de entrada. En el vértice, entre la sección convergente y la garganta, la cual está ubicada en la distancia 38 mm, se produce una caída abrupta de la presión, incluso se presenta una presión negativa para el perfil k − e con celdas cuadriláteras para la simulación del experimento 4, y lo mismo sucede para los perfiles k −e y k −ω con celdas cuadriláteras para la simulación del experimento 5. Asimismo, se produce en la región del otro vértice que se encuentra en el extremo derecho de la garganta en la distancia 54 mm, con caída de presión de menor intensidad, pero sin presencia de presión negativa.
En la sección de la garganta, un tramo de los perfiles tiene un comportamiento convexo, separado uno del otro, quedando en el siguiente orden, de abajo hacia arriba: el perfil k − e y el perfil k − ω, ambos simulados con el dominio con malla con celdas cuadriláteras, seguidamente el perfil k − e y el perfil k − ω, ambos simulados con el dominio con malla de celdas triangulares. Y se observa cómo quedan posicionados los cinco datos experimentales de presión en la referencia D. Los tramos de las trayectorias de los perfiles k-e con celdas cuadriláteras tienen mayor acercamiento con los datos experimentales. Señalando que la caída de la presión en la garganta se produce porque el flujo pasa con mayor velocidad por la sección estrecha, producto de la alta diferencia de presión del flujo entre la entrada y la salida del tubo Venturi.
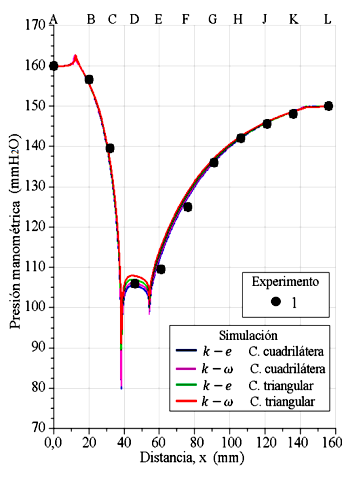
Figura 12. Experimento 1 de presiones de columnas de agua, y perfiles de presiones evaluados en la pared del tubo Venturi. Presión en (mmH2O): 160 mm en la entrada y 150 mm en la salida.
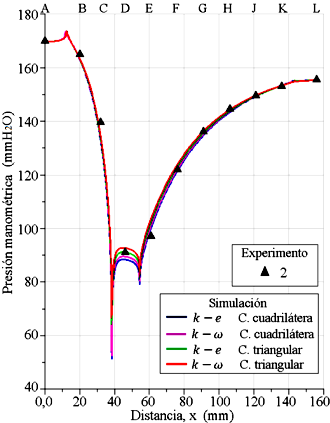
Figura 13. Experimento 2 de presiones de columnas de agua, y perfiles de presiones evaluados en la pared del tubo Venturi. Presión en (mmH2O): 170 mm en la entrada y 155,5 mm en la salida.
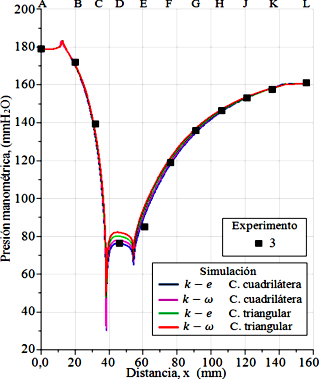
Figura 14. Experimento 3 de presiones de columnas de agua, y perfiles de presiones evaluados en la pared del tubo Venturi. Presión en (mmH2O): 179 mm en la entrada y 161 mm en la salida.
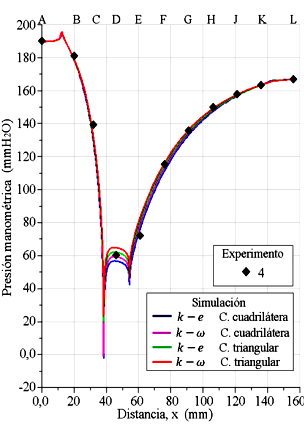
Figura 15. Experimento 4 de presiones de columnas de agua, y perfiles de presiones evaluados en la pared del tubo Venturi. Presión en (mmH2O): 190 mm en la entrada y 167 mm en la salida.
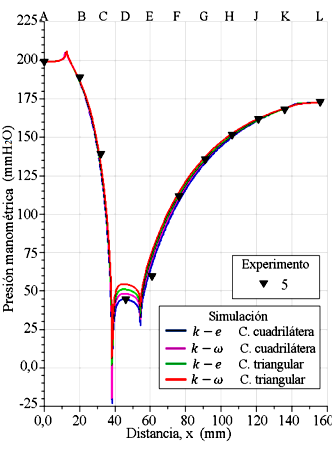
Figura 16. Experimento 5 de presiones de columnas de agua, y perfiles de presiones evaluados en la pared del tubo Venturi. Presión en (mmH2O): 199,5 mm en la entrada y 173 mm en la salida.
Los resultados numéricos y los datos experimentales en la referencia D se muestran en la Tabla 11. Donde el modelo de turbulencia k−e estándar presentó el mayor error porcentual de 5,88 % para el experimento 4, y para k − ω estándar fue de 7,84 % para el experimento 5, y menores de estos valores para los demás resultados, esto es, para el mallado con celdas cuadriláteras. Y para la malla con celdas triangulares, correspondiente al experimento 5, k − e estándar presentó el error porcentual de 14,17 %, y k − ω estándar de 21,66 %, y menores para los demás resultados.
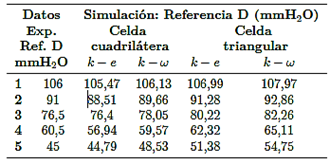
Tabla 11. Datos experimentales y numéricos para la referencia D, para dos modelos de turbulencia y dos tipos de mallas aplicadas
Los perfiles de presiones para el modelo de turbulencia k − e estándar, simulado el flujo con el dominio mallado con celdas cuadriláteras, y los datos experimentales de presión presentados en la Tabla 5 y graficada en la Figura 6, se presentan en la Figura 17, donde se observa que las trayectorias de los perfiles satisfacen la validación con los datos experimentales. En la referencia D, ubicada en la sección de la garganta, las trayectorias de los perfiles son convexas. Aunque no se presenta una gráfica similar a la Figura 17 para el modelo de turbulencia k − ω estándar, este modelo también tiene validez aunque con un margen de resultados numéricos ligeramente variados con respecto al modelo de turbulencia k − e estándar, tal como se muestran en los resultados de la Tabla 12, anteriormente presentada. Del análisis realizado, los resultados numéricos están influenciados por el tipo de malla aplicado al dominio computacional, siendo la malla estructurada con celdas cuadriláteras la que aporta resultados numéricos más precisos con respecto a la malla con celdas triangulares.
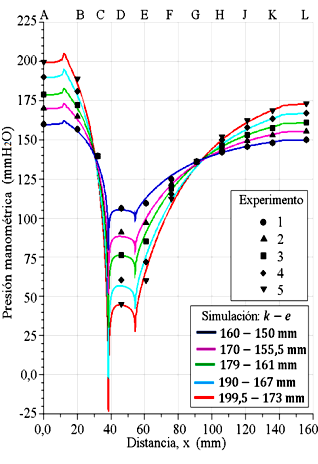
Figura 17. Datos experimentales de presiones de columnas de agua y perfiles de presiones evaluadas en las paredes del tubo Venturi con el modelo de turbulencia k − e estándar.
Las presiones del flujo a lo largo de la simetría axial del eje x, son comparadas con los datos experimentales de las presiones en las paredes del tubo Venturi, se muestran en la Figura 18. Los perfiles se interceptan unos con otros en las referencias C y G, y se observa cómo evolucionan las trayectorias de las caídas de presiones en el extremo izquierdo de la referencia D y del incremento de las presiones en el extremo derecho de la misma referencia, siendo las trayectorias de las curvas cóncavas en el tramo de la sección de la garganta. También se muestran las ligeras separaciones de los perfiles de los datos experimentales, por lo cual, las magnitudes de las presiones en cada una de las referencias son ligeramente mayores y otras ligeramente menores con respecto a los datos experimentales de las presiones de las paredes. Los perfiles fueron obtenidos para el dominio mallado con celdas cuadriláteras y el modelo de turbulencia k − e estándar.

Figura 18. Datos experimentales de presiones de columnas de agua y perfiles de presiones evaluados en la simetría axial (eje x) del tubo Venturi con el modelo de turbulencia k − e estándar.
Al comparar los resultados numéricos de la Figura 18 con la Figura 17, se evidencia para las ubicaciones de las referencias A, B, C, D, E, F, G, H, J, K y L, las presiones tienen tendencia a ser perpendiculares al eje x y a las paredes, formando una trayectoria de curvas conocidas como isóbaras. Sin embargo, donde se dan las uniones de las secciones, en los vértices, la configuración de las trayectorias de las curvas tiene comportamiento distinto producto de variaciones bruscas de presiones, inducido por el perfil geométrico de la sección de contracción gradual y expansión gradual del tubo Venturi.
En la Figura 19, como detalle, unificando las Figuras 17 y 18, para la distancia en el rango de 30-100 mm, se muestran tramos de perfiles superpuestos, para las presiones en las paredes y en el eje x, los cuales son comparados con los datos experimentales para las referencias C, D, E, F y G. Se observa las caídas de presiones en los extremos de la garganta y cómo las curvas se interceptan y bordean los datos experimentales.
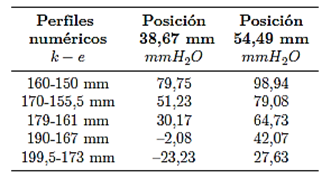
Se muestra que las caídas abruptas de las presiones numéricas en la pared se producen para la posición de 38,67 mm, al inicio de la garganta; y las otras caídas de presiones se presentan en la posición de 54,49 mm, la cual está ubicada al inicio de la sección divergente.

Figura 19. Datos experimentales para las referencias C, D, E, F y G, y tramos de perfiles de presiones evaluados en las paredes y en el eje x del tubo Venturi con el modelo de turbulencia k − e estándar.
En la Tabla 12 se muestran los valores numéricos de las caídas de presiones en la pared en los extremos de la sección de la garganta. Se muestra que la menor caída de presión numérica se presenta en la posición 38,67 mm, para la curva identificada 199,5-173 mm lo cual corresponde para el experimento 5, siendo la magnitud de la caída de presión de –23,23 (mmH2O), y como es una presión negativa, se evidencia que es una presión de succión; así mismo, se tiene para la curva 190-167 mm para el experimento 4 y para la misma posición, una presión de –2,08 (mmH2O).
En el vértice, donde se presenta la presión negativa, corresponde para una región ínfima de un radio de acción estimada de 0,2 mm, donde, la presión negativa es un resultado inesperado, ya que el perfil hidrodinámico de la pared interna del tubo Venturi que mide el caudal, la sección convergente tiene un ángulo medio de diseño, y es con el fin de evitar presencia de presiones negativas.
Asimismo, se resalta que, durante el experimento 4 y 5 no se observaron en el vértice ubicado a la entrada sección de la garganta presencia alguna de burbujas de aire en esa región y aguas abajo como señal de indicios de cavitación. Por lo cual, el resultado numérico obtenido de la presión negativa, induce a investigar con instrumentos sensibles para captar las posibles burbujas de aire de dimensiones imperceptibles al ojo humano que pudieran estar presentes. Por lo cual, se debe verificar simulando el flujo con otros modelos de turbulencia en trabajo a futuro, para determinar si se presentan o no presiones negativas, y así obtener conclusiones cercanas a la realidad del fenómeno físico.
De la comparación de los resultados numéricos con los datos experimentales, se evidencia que la simulación numérica arroja resultados satisfactorios sustentados en un rango de errores porcentuales aceptables a nivel de ingeniería, por lo cual, quedan validados los modelos de turbulencia k − e estándar y k − ω estándar. Estos dos modelos de turbulencia validados fortalecen su aplicación en la dinámica de fluidos computacional en la simulación del flujo en dominios computacionales para geometrías simples o complejas en el campo de la ingeniería, y permiten determinar la magnitud de algún parámetro físico que no es posible obtener mediante instrumentos de medición y ecuaciones analíticas.
4. Conclusiones
Según los análisis realizados, para los casos de estudio experimental y numérico, se concluye que: Los caudales numéricos obtenidos para los modelos de turbulencia k−e estándar y k−ω estándar, al ser comparados con los cinco datos de caudales experimentales, arrojaron errores porcentuales en el rango de 1,01-9,68 %. Así mismo, se determinó el error porcentual en el rango de 1,01-9,68 % para el número de Reynolds. Donde, para los cinco experimentos, el número de Reynolds está en el rango de 12000<Re<32300; y para las simulaciones numéricas, en el rango 12100<Re<34400.
Los cinco resultados experimentales de las presiones obtenidos en las referencias C y G, donde los diámetros del tubo Venturi allí son diferentes, las presiones en ese lugar no varían su magnitud por más que se incrementa la velocidad del flujo en dichas referencias por el aumento del caudal. Además, la menor caída de presión se produce en la parte media de la sección de la garganta por el efecto Venturi.
Los perfiles obtenidos con los modelos de turbulencia k − e estándar y k − ω estándar y que fueron comparados con los datos experimentales de presión, el que arrojó resultado más preciso fue el modelo de turbulencia k − e estándar para el dominio mallado con celdas cuadriláteras, donde los resultados numéricos se ajustaron más a los datos experimentales en la parte media de la sección de la garganta, la cual es una sección crítica por la caída abrupta de la presión del flujo. Lo cual evidencia que el tipo de mallado influye en los resultados numéricos.
En los extremos de la sección de la garganta, en las posiciones 38,67 mm y 54,49 mm, las caídas de presión fueron más abruptas que en la parte media de la garganta, presentándose presiones negativas en la posición 38,67 mm, para las curvas numéricas correspondiente para el experimento 4 y 5.
La menor caída de presión en la pared no se produce en la parte media de la sección de la garganta, sino en los extremos de la misma, para el tubo Venturi estudiado.
En trabajos a futuro, para estudios experimentales del mismo tipo de tubo Venturi, se recomienda manipular la válvula de control, y con los resultados experimentales a obtener, realizar las comparaciones respectivas con los resultados experimentales del presente trabajo.
Asimismo, para casos de estudios numéricos, se recomienda emplear otros códigos de la CFD para simular el flujo de agua empleando otros modelos de turbulencia, y comparar con los resultados numéricos del presente trabajo.
Agradecimientos
Mi agradecimiento a Jehová, mi Dios todopoderoso, mi fuente de sabiduría e inspiración. Al Departamento de Ingeniería Mecánica de la Universidad Nacional Experimental Politécnica “AJS” Vice-Rectorado Puerto Ordaz (UNEXPO), Bolívar, Venezuela. Al Grupo de Modelamiento Matemático y Simulación Numérica (GMMNS, Group of Mathematical Modeling and Numerical Simulation) de la Universidad Nacional de Ingeniería (UNI), Lima, Perú.