Forma sugerida de citación:
Contreras Urgilés, W.; Maldonado Ortega, J. y León Japa, R. (2019). «Aplicación de una red neuronal feed-forward backpropagation para el diagnóstico de fallas mecánicas en motores de encendido provocado». Ingenius. N._ 21, (enero-junio). pp. 32-40. doi: https://doi.org/10.17163/ings.n21.2019.03.
Introducción
En la actualidad en el área del transporte automotor los operarios y técnicos utilizan diagramas rudimentarios para el diagnóstico y reparación de motores de encendido provocado (MEP), lo que implica, subjetividad en el diagnóstico, desventajas en el tiempo de detección de fallas, falta de asertividad, y como consecuencia, se tienen altos costos de mantenimiento.
Por todo lo antes expuesto, es necesario aplicar nuevas metodologías y técnicas especializadas para conseguir diagnósticos en tiempos cortos que optimicen recursos para la detección de fallos en motores de vehículos a gasolina [1].
La complejidad de análisis e interpretación de parámetros de operación que intervienen en el MEP hace necesario el uso de redes neuronales y matemática computacional para un eficiente diagnóstico de fallos mecánicos en motores de ciclo Otto. La investigación de Howlett [2] muestra que mediante el análisis de la señal de la bujía con redes neuronales artificiales se puede monitorear el MEP para un diagnóstico o control de fallas.
De igual forma Antory [3] indica que es posible determinar con precisión diferentes tipos de fallas comunes en un motor diésel para automóviles mediante un modelo de diagnóstico que utiliza una variante de redes neuronales auto asociativas (AANN).
Estrategias paralelas a las redes neuronales son aplicables para el diagnóstico de fallos en el campo automotor. Chen y Zhao [4] aplican una variante paralela de las RNA conocidas como redes de base radial RBF, esta técnica es utilizada para el diagnóstico de fallas del sistema de combustible en el motor.
Se pueden aplicar estrategias paralelas para entrenar una RNA, por ejemplo, el entrenamiento de la red Elman modificada aplicada para el diagnóstico de fallas del motor. Dicho método es muy efectivo y puede obtener un buen resultado de diagnóstico, debido a que es una red recurrente y tiene una relación dinámica de entrada y salida [5], asimismo Lian et al. [6] presentan un método de diagnóstico para detección de fallas en motores de encendido provocado basado en la aplicación de lógica difusa y redes neuronales. Shah et al. [7] proponen un sistema de reconocimiento de fallas para motores de combustión interna, con aplicación de la transformada de wavelet discreta (DWT) y la técnica de redes neuronales de base radial (RBFN).
Cay [8] desarrolló un modelo de RNA basado en el algoritmo de retro propagación para un MEP con el objetivo de predecir el consumo de combustible específico del freno, la potencia efectiva y la temperatura de escape del motor. Cay et al. [9] presentaron un modelo de RNA capaz de predecir el rendimiento del MEP y las emisiones de escape en un motor que funcionaba con metanol y gasolina.
Las redes neuronales tienen diversas aplicaciones en la calibración de motores de encendido por chispa. R. F. Turkson et al. [10] han propuesto que aquellas permiten la identificación del sistema para el prototipado rápido, la detección virtual, estrategias de control emergentes y aplicaciones de diagnóstico a bordo (OBD).
Otra importante aplicación de las redes neuronales (ANN) con modelos cinéticos como funciones de activación para las neuronas en la capa oculta es aplicable para el estudio de degradación del poliuretano de un colector de admisión automo- triz con tratamiento isotérmico [11].
El sistema de diagnóstico propuesto puede detectar fallos en motores de encendido provocado que no son detectadas por la ECU (Engine Control Unit). El sistema se sustenta en la utilización de las señales de los sensores MAP y CMP, ya que tienen la facultad de reducir al mínimo el tiempo de diagnóstico, esto último evita usar técnicas intrusivas en el MEP como por ejemplo el uso de manómetros para medición de compresión de cilindros y presión de combustible, vacuómetro, escáner automotor, entre otras. Las técnicas antes indicadas tienen la función de determinar el fallo mecánico.
Materiales y métodos
En la presente sección se desarrollan las temáticas principales que tienen que ver con la selección de unidad experimental e instrumentación mínimamente invasiva, condiciones de toma de muestras, metodología para la adquisición de datos, obtención de matriz de atributos, reducción de atributos, selección de atributos para entrenamiento de la RNA y algoritmo de la red neuronal en Matlab.
Selección de la unidad experimental e instrumentación mínimamente invasiva
Se toma en consideración como principal objetivo evitar el desarmado de elementos y piezas del motor para diagnosticar fallas mecánicas, por lo que se determina medir la depresión del motor mediante la instalación de un sensor tipo MAP en una toma de vacío del múltiple de admisión, ubicándolo después de la mariposa de aceleración, de tal manera que la conexión no afecta el funcionamiento del motor.
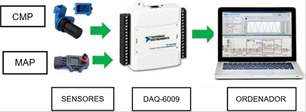
La identificación de cada uno de los cilindros se realiza mediante el registro de la señal del sensor CMP. En la Figura 1 se presentan la unidad experimental puesta a prueba Motor Hyundai Sonata 2.0 DOHC, una computadora personal (PC), tableta, Ni DAQ-6009 y la interfaz del escáner automotor. En la Figura 2 se muestra la conexión del sensor MAP, la toma de vacío en el múltiple de admisión y la herramienta de adquisición de datos Ni DAQ-6009.
Condiciones de toma de muestras
Se utiliza el software Labview 2017 junto con una tarjeta Ni DAQ-6009, para la obtención de muestras. Las muestras se adquieren en ralentí aproximadamente a 850 rpm con un rango de temperatura del MEP de entre 92 °C y 97 °C, carga del motor de 40 % y se aplica el escáner automotor para corroborarlas. Según un estudio preexperimental se determina que la señal del sensor MAP posee picos de mayor frecuencia, de tal manera que se realiza la toma de muestras a una velocidad de 10 KHz en un tiempo de 5 segundos para cada una de las señales, dicha velocidad supera el criterio de Nyquist (1.416 KHz).
Metodología para la obtención de datos
En la Figura 3 se presentan los elementos físicos necesarios para el muestreo de señales.
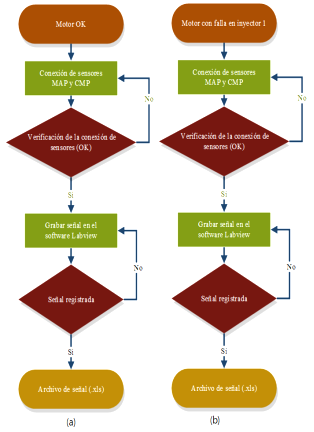
Para obtener los datos de las señales de los sensores MAP y CMP se sigue el flujograma de proceso que se presenta en la Figura 4.
El proceso de obtención de datos se inicia con la revisión del motor en correcto funcionamiento o falla supervisada, posterior a ello se procede a inspeccionar la conexión de los sensores. Si la conexión es correcta, se graba la señal con el software Labview y se registra en un archivo de Excel, de lo contrario, se procede a verificar la conexión de los sensores. Para registrar las señales se aplica el procedimiento antes descrito tanto para el caso de motor en buen funcionamiento como para el motor con falla supervisada, Figura 4(a); 4(b).
En la Tabla 1 se indica el total de 18 fallas que se generan en la unidad experimental, cada una con su respectivo código de identificación; también se indica la condición del motor en óptimo funcionamiento.
Obtención de matriz de atributo
Una vez desarrollada la adquisición de señales temporales se procedió a elaborar un algoritmo en el software Matlab para lectura y obtención de matriz general de atributos. Dichos atributos son los siguientes: media geométrica, máximo, mínimo, mediana, covarianza, varianza, desviación estándar, moda, factor de curtosis, coeficiente de asimetría, energía, potencia, área bajo la curva, entropía, coeficiente de variación, rango, raíz media cuadrática y factor de cresta.
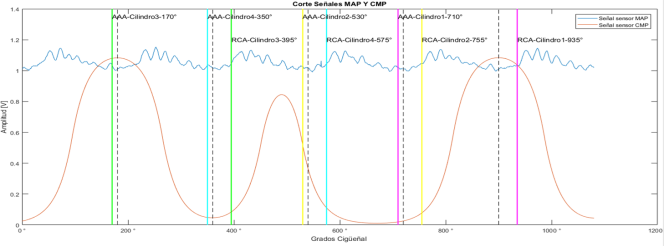
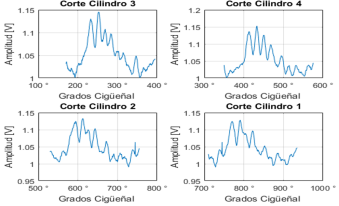
En la Figura 5 se ilustra el corte completo de un ciclo del motor (720° ± 180°), con el reglaje de distribución de adelanto a la apertura de admisión (AAA) y retraso de cierre de admisión (RCA), correspondiente a cada uno de los cilindros, del cual se realiza un ventaneo que se observa en la Figura 6 y se obtiene la caracterización de la señal.
Reducción de atributos
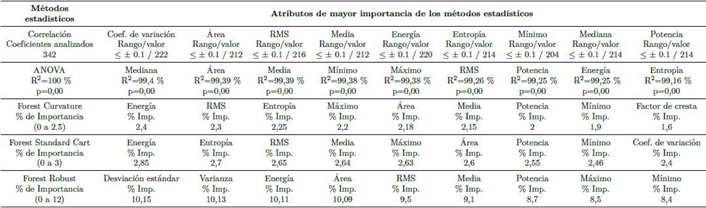
Para la selección y reducción del número de atributos se analiza la matriz general a través de 3 métodos estadísticos: ANOVA, matriz de correlación y Random Forest.
La aplicación del método estadístico ANOVA de un solo factor, permite determinar los mejores atributos que ingresan a la matriz general mediante el análisis de los 18 atributos. Tomando en consideración en el método el mayor valor de R2, puesto que los valores cercanos al 100 % indican que existe un correcto ajuste de los datos al modelo, es decir, se determina la variación entre los atributos. Además, en el método se consideran los valores de p próximos a 0 que determinan si los atributos son estadísticamente significativos [12].
Respecto a la matriz de correlación, se descartaron los atributos que contienen coeficientes próximos a -1 o 1, dado que con los mismos existe una relación fuerte entre las variables, ya sea negativa (-1) o positiva (1). En efecto se seleccionaron los atributos con coeficientes próximos a cero, puesto que con estos atributos no existe una correlación fuerte entre las variables [13].
En cuanto al método de Random Forest, permite obtener la estimación de importancia de atributos con uso de los métodos de Curvature test, Standard CART e Interaction test. Posterior a ello, se aplicó el análisis de Pareto para seleccionar los atributos de mayor prioridad, considerando solo el primer 95 % de la distribución acumulada [14].
Los resultados de los métodos estadísticos aplicados: ANOVA, matriz de correlación y Random Forest se observan en la Tabla 2.
La matriz general contiene los 18 atributos correspondientes a las 19 condiciones inducidas a la unidad experimental.
Reducción de atributos
Para la selección y reducción del número de atributos se analiza la matriz general a través de 3 métodos estadísticos: ANOVA, matriz de correlación y Random Forest.
La aplicación del método estadístico ANOVA de un solo factor, permite determinar los mejores atributos que ingresan a la matriz general mediante el análisis de los 18 atributos. Tomando en consideración en el método el mayor valor de R2, puesto que los valores cercanos al 100 % indican que existe un correcto ajuste de los datos al modelo, es decir, se determina la variación entre los atributos. Además, en el método se con- sideran los valores de p próximos a 0 que determinan si los atributos son estadísticamente significativos [12].
Respecto a la matriz de correlación, se descartaron los atributos que contienen coeficientes próximos a –1 o 1, dado que con los mismos existe una relación fuerte entre las variables, ya sea negativa (–1) o positiva (1). En efecto se seleccionaron los atributos con coeficientes próximos a cero, puesto que con estos atributos no existe una correlación fuerte entre las variables [13].
En cuanto al método de Random Forest, permite obtener la estimación de importancia de atributos con uso de los métodos de Curvature test, Standard CART e Interaction test. Posterior a ello, se aplicó el análisis de Pareto para seleccionar los atributos de mayor prioridad, considerando solo el primer 95 % de la distribución acumulada [14].
Los resultados de los métodos estadísticos aplicados: ANOVA, matriz de correlación y Random Forest se observan en la Tabla 2.
Selección de atributos para entrenamiento de la RNA
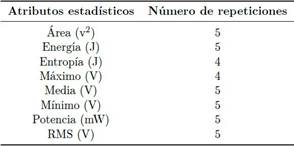
Para seleccionar los atributos que serán considerados en la entrada de la red neuronal se realizó un análisis de coincidencia en la Tabla 2 en el cual se seleccionaron los atributos que más se repiten entre los resultados de cada método estadístico aplicado. Los atributos que más se repiten se muestran en la Tabla 3, corroborando la efectividad de cada método utilizado.
Algoritmo de la red neuronal en Matlab
Mediante el uso de la plataforma de RNA del software Matlab se realizaron diferentes configuraciones para obtener una generalización de la red con un mínimo error.
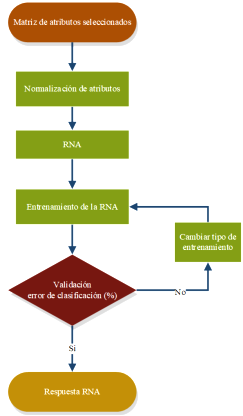
En la Figura 7 se presenta el flujograma de la creación de la RNA.
El algoritmo inicia con la lectura de la matriz de entrada y respuesta respectiva para la RNA. Luego se normaliza el vector de entrada y la respuesta con el valor máximo de cada matriz con el objetivo de optimizar la creación de la RNA. Una vez normalizada la matriz de atributos se procedió a la creación de la RNA.
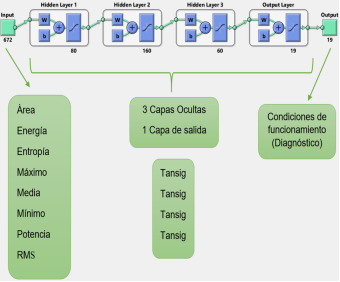
En la Figura 8 se observan los parámetros de la creación de la RNA de tipo feed-forward backpropagation.
Una vez creada la red, se procedió a entrenar la red neuronal, y para ello se consideraron los siguientes parámetros para el entrenamiento:
Con la red neuronal previamente entrenada se verificó el error de clasificación, si el error es mayor al 5 %, se procede a cambiar los parámetros para disminuir el error de clasificación.
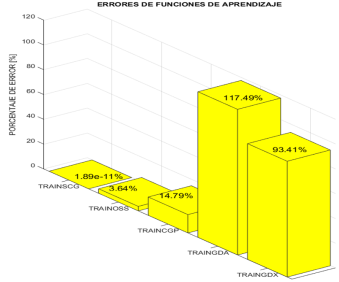
En la Figura 9 se ilustran los errores de clasificación de diferentes configuraciones de entrenamientos obtenidos con el objetivo de conseguir la red neuronal con el menor error posible.
La red neuronal con una función de entrenamiento trainscg utilizada para el sistema de diagnóstico presentó un error de 1.89e−11 %.
En la Figura 10 se presentan los resultados del coeficiente de correlación de Pearson R de la red neuronal creada, la cual es facilitada por el código de entrenamiento red.trainFcn = ’trainscg’ del software Matlab.
Las líneas indican los valores esperados y los círculos negros representan los valores pronosticados por la RNA. La predicción determinada por la red neuronal es eficiente y se corrobora con un buen desempeño, dado que se obtiene un índice global de 1 en entrenamiento, validación y prueba lo que indica una relación lineal fuerte positiva entre las condiciones reales del MEP y los resultados proporcionados por la red neuronal [15].
En la Figura 11 se muestra la comparación entre la respuesta de la red neuronal con el resultado esperado, es decir, se observan las 19 condiciones mecánicas reales del motor identificadas por la red neuronal.
Resultados y discusión
A fin de comparar el correcto funcionamiento del sistema de diagnóstico se procede a realizar varias pruebas bajo diversas condiciones de funcionamiento.
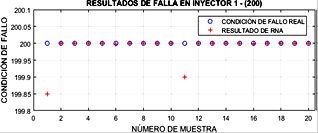
En este apartado se presentan dos condiciones de falla en específico: el inyector 1 (200) y el fallo en bobina 2-3 (1100).

Figura 11. Red neuronal con porcentaje de error de 1.89e−11, con función de entrenamiento «trainscg».
En la Figura 12 se muestran los resultados de los valores obtenidos por la RNA para las condiciones de funcionamiento cuando el inyector 1 se encuentra con falla, y donde el valor promedio del error del resultado de la red neuronal y la condición real es 0.0127.
En la Figura 13 se muestran los resultados de los valores obtenidos por la RNA para condiciones de funcionamiento cuando la bobina 2-3 se encuentra con falla y el valor promedio del error del resultado de la red neuronal y la condición real es 0.0060.
Obtenidos los resultados de las condiciones funcionales del MEP, se puede destacar que la diferencia entre las respuestas tanto de condición real y como de respuesta de red neuronal tienen un valor próximo a cero. Por lo tanto, la aplicación del sistema de diagnóstico es capaz de detectar la condición funcional de falla verdadera.
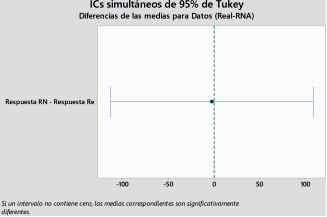
En efecto en la Figura 14 se observa que al agrupar los datos mediante el método estadístico de Tukey con un índice de confianza de 95 % de las respuestas obtenidas de la RNA y de la condición real del motor, se determina que las medias son equivalentes y no existe una diferencia estadísticamente significativa, ya que las medias de cada una de las respuestas coinciden en un valor próximo a cero.
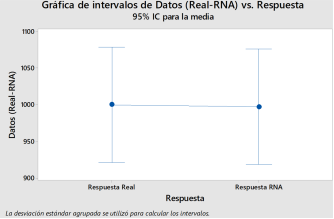
Además, la Figura 15 de intervalos indica que no existe diferencia entre los promedios de las pruebas en las diferentes condiciones funcionales del motor.
Asimismo, en la Figura 16 se corrobora que existe una relación entre la respuesta esperada y de la red neuronal ya que comparten la misma letra de agrupación (A) y el valor p (p-value) es igual a 0.965. Dando como resultado un valor de confiabilidad del 96,5 %, siendo este valor muy aceptable para temas de diagnóstico de motores de combustión interna de encendido provocado.
Conclusiones
El modelo de red neuronal desarrollado posee un error de clasificación de 1.89e−11 con la función de entrenamiento trainscg, lo que permitió la identificación precisa de los diferentes tipos de condiciones mecánicas del MEP, por lo que constituye una alternativa claramente viable para ser integrada en un sistema de diagnóstico, debido a la rapidez computacional que ofrecen las redes neuronales artificiales.
Mediante el desarrollo del análisis de varianza de un solo factor, se obtuvo un valor de p (p-value=0,965) demostrando que la respuesta real de clasificación de fallas mecánicas es equivalente al resultado obtenido mediante la RNA, de manera que con este valor se demuestra que no existe una diferencia estadísticamente significativa.
En este trabajo se muestra que la aplicación de redes neuronales (feed-forward backpropagation) es válida para la detección de condiciones de fallas mecánicas en motores de encendido provocado; además, la técnica de diagnóstico aplicada presenta la ventaja de evitar el desarmado de elementos y piezas del motor con una técnica mínimamente invasiva fiable y de gran precisión. Para determinar los mejores atributos para el entrenamiento de RNA se aplicó diferentes mpetodos estadísticos: análisis de varianza (ANOVA), matriz de correlación, Random Forest, de los cuales se agrupó los resultados en una matriz general que permitió escoger los de mayor coincidencia e importancia para la diferenciación de patrones de fallas mecánicas.