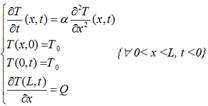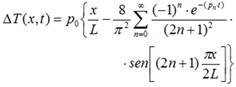Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introducción
Desde hace años existe el interés en el desarrollo de nuevos métodos para determinar la conductividad y difusividad térmicas de los compuestos. Esto se debe, en gran medida, al rápido avance de la ciencia de materiales y sus múltiples aplicaciones [1–14]. Existen los métodos estacionarios que, sin embargo, presentan la desventaja del prolongado tiempo de exposición al calor que sufre la muestra, aumentando considerablemente su temperatura y, por lo tanto, pudiendo incidir en la variación de sus características térmicas [6], [15], [16].
En los materiales heterogéneos es más compleja la determinación de los valores exactos de los parámetros térmicos por su composición [17-25]. Los materiales compuestos pueden ser representados por medios laminados, fibrosos, granulares, etc., [24]. Existen algunos estudios para medir la conductividad térmica efectiva de estos, aunque, en general, presentan limitaciones con la continuidad de las fases de un material a otro; por lo que incluso se pueden presentar fases adicionales [17]. Asimismo, la geometría de los mismos es un inconveniente debido a que, en la práctica, no todas las partículas tienen la misma forma y tamaño; variando considerablemente el factor de forma, que se toma en cuenta en algunas fórmulas para el cálculo de propiedades de los compuestos [17], [18], [24], [26]. Por lo tanto, los métodos matemáticos de la física son una alternativa necesaria a tener en cuenta para determinar las propiedades efectivas de materiales compuestos.
El presente trabajo tiene como objetivo calcular numéricamente la conductividad y difusividad térmicas efectivas en compuestos sólidos heterogéneos, mediante la simulación computacional a través del análisis por elementos finitos; considerando que, el mecanismo de propagación de calor solo tiene lugar por conducción. Se emplea un método no estacionario que aprovecha la radiación luminosa como fuente externa de calor y constante que incide sobre uno de los extremos (x = L) de una barra térmicamente aislada, en el otro extremo (x = 0); la temperatura se mantiene constante (entre 10 y 20 °C). El flujo de calor se mide en régimen no estacionario por lo que posee la ventaja de ser una medición relativamente rápida y con un mínimo aumento de temperatura; de esta manera, se evita las pérdidas por radiación. Asimismo, para calcular las propiedades térmicas no se necesita conocer ni las características térmicas ni geométricas de los materiales que integran el compuesto, contrario de otros trabajos [17-26].
2. Materiales y métodos
2.1. Metodología de la simulación
Se estudia, en primer lugar, una barra homogénea de cobre de 0,15 m de longitud, con una sección cuadrada de lado igual a 0,007 m como indica la Figura 1. El software utilizado SolidWorks® 2016 (Licencia: 9710 2117 5072 9710 M4R6 FH89), muestra la distribución de temperatura para todos los puntos de la barra a partir del calentamiento de uno de los extremos (x = L), en función del tiempo.
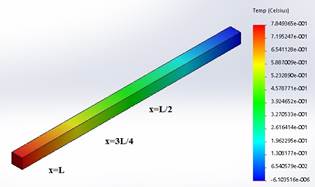
Figura 1. Distribución de la temperatura a lo largo de una barra de cobre de sección cuadrada de longitud L = 0,15 m y lado a = 0,007 m. Con estas dimensiones se garantiza las características unidimensionales del sistema propuesto.
Luego de este primer estudio con un material homogéneo conocido se comprueba que los valores de conductividad (χ) y difusividad (α) térmicas se ajustan satisfactoriamente [27].
En la segunda etapa, se reproduce la simulación, esta vez se obtiene la distribución de la temperatura a lo largo de una barra de cobre de sección cuadrada con cuatro inserciones de plomo de 0,003 m de longitud y 2,1 10-5 m2 de área de sección transversal, de tal forma que se obtiene un compuesto de cobre (65,7 %)-plomo (34,3 %), como indica la Figura 2.
Figura 2. Distribución de la temperatura a lo largo de un material compuesto de cobre (65,7 %)-plomo (34,3 %) en forma de barra de longitud L = 0,15 m y lado a = 0,007 m; con cuatro inserciones de plomo de 0,003 m de longitud y 2,1·10-5 m2 de área de sección transversal.
En las Figuras 1 y 2, los valores de temperaturas que se muestran en la distribución sobre cada punto de las barras son las temperaturas alcanzadas en estado estacionario: ΔTes. Sin embargo, para calcular la conductividad y difusividad térmicas bajo este método no se necesita llegar a ese valor, como se describe a continuación.
2.2. Aspectos teóricos
En el estudio de la propagación del calor en una barra sólida se tiene en cuenta solo el proceso de conducción a lo largo de la misma; las pérdidas de calor por convección y radiación deben ser minimizadas. En este sentido, gracias a un adecuado diseño experimental se logra este propósito. A saber: 1) el poco aumento de la temperatura ΔT evita pérdidas por radiación, 2) por ser una barra sólida no se aprecia la convección; de forma tal que se puede aplicar la ecuación parabólica del calor para conocer la distribución de temperaturas en toda la barra.
donde:
Homogeneizando las condiciones de frontera, teniendo en cuenta el método de separación de variables, se obtiene el incremento de la temperatura como función del tiempo t y la coordenada x; cuya solución es [28]:
donde: 
que representa la variación de temperatura alcanzada en el estado estacionario, q es el calor, L la longitud de la barra, A el área de la sección transversal, la conductividad térmica y pn = pn (α,n), es función de la difusividad térmica y de los términos dentro de la serie. Está asociado con el tiempo que se demora el sistema en alcanzar el estado estacionario e igualmente con la frecuencia con que oscilan los valores de temperatura en cada punto de la barra mientras avanza el tiempo.
Utilizando el método de los mínimos cuadrados se ajustan los puntos de la simulación a la ecuación (2) mediante el programa Mathematica® 11.0 (Licencia: 3657-5751-TEGG73). El número de términos de la sumatoria se calcula aproximadamente, de manera que en x = L y t = 0 la variación de temperatura que se aprecie por el sensor que mide sea igual a cero, o sea: ΔT(l, 0) = 0. A partir de los valores obtenidos para p0 y pn se determinan los correspondientes de conductividad y difusividad térmicas.
3. Resultados y discusión
3.1. Barra de cobre
Se muestran los resultados de la primera etapa en donde se trabajó con la barra de cobre. Se puede apreciar en la Figura 3, una convergencia absoluta entre la solución teórica de la ecuación (2) y los datos arrojados por la simulación para los diferentes valores de la coordenada x, en que fue monitoreado.
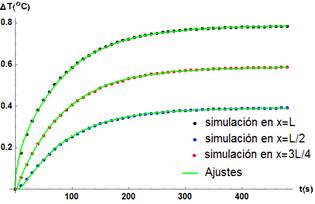
Figura 3. Gráfico del ajuste de la distribución de temperatura vs. tiempo cuando se calienta la barra de cobre en la posición (x = L). Se tiene una convergencia absoluta entre simulación y modelo en los tres puntos de monitoreo.
De tal forma se obtuvo los valores de conductividad y difusividad térmicas presentados en la Tabla 1 y, como se aprecia, la coincidencia entre los valores para distintas posiciones es notoria. Esto indica que, obviamente, las características térmicas no dependen de la coordenada si hablamos de un material homogéneo. Asimismo, los valores calculados de conductividad y difusividad térmicas se aproximan significativamente a los ya reportados, con un error relativo promedio de solo 0,01% y 0,7% en la conductividad y difusividad térmicas respectivamente [27].
Tabla 1. Comparación entre los valores de conductividad χ[W/m °C] y difusividad α · 10−6[m/s2] térmicas reportados y los calculados en tres puntos diferentes de una barra de cobre homogénea.
Figura 4. Gráfico de la variación de la temperatura en función del tiempo t y la coordenada x, para la barra de cobre homogénea: q = 0,1 W; A = 4,9·10-5m2; L = 0,15 m.
En la Figura 4 se aprecia el gráfico de la distribución de temperatura en función de la coordenada x y el tiempo t, según la ecuación (2), con los valores de y obtenidos en la Tabla 1, q = 0, 1W, A = 4, 9.10-5 m2, L = 0, 15 m. Nótese que, el aumento de temperatura es pequeño (menor a un grado) lo que resulta conveniente a la hora de poner en marcha esta medición en el laboratorio.
3.2. Compuesto
A continuación, en la Figura 5 se muestra los resultados de la segunda etapa, donde se trabajó con un compuesto como indica la Figura 2.
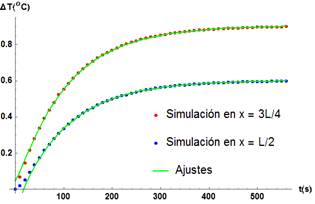
Figura 5. Gráfico del ajuste de la distribución de temperatura vs. tiempo cuando se calienta el compuesto (cobre 65,7 % - plomo 34,3 %) en la posición x = L. Se tiene una convergencia absoluta después de los primeros 30 s.
Se debe acotar que, en esta segunda etapa se monitoreó la variación de temperatura en las posiciones x = 3L/4 y x = L/2, debido a que están inmersas dentro del compuesto. Igualmente, en la Figura 5 se observa que el modelo comienza a ajustarse absolutamente después de los primeros 30 segundos a partir de que comienza a recibir el calor por el extremo x = L.
Esta discrepancia puede estar asociada a la baja conductividad térmica del plomo de forma tal que, en las posiciones x = 3L/4 y x = L/2, aún no llega un flujo de calor significativo al comienzo; por lo que los datos resultan un poco dispersos, esto se puede solucionar aumentando la potencia de q en x = L.
Tabla 2. Valores de conductividad χ [W/m °C] y difusividad α·10−6[m/s2] térmicas efectivas calculados en dos puntos diferentes del compuesto.
En la Tabla 2 aparecen los resultados de la conductividad y difusividad térmicas efectivas calculadas para el compuesto. Como se aprecia, los valores efectivos tanto de χ como de α se encuentran en el intervalo entre los valores del plomo y cobre, por lo que, el resultado es lógico y adecuado. En segundo lugar, se nota precisión (si bien no significa total exactitud) en los resultados pues, ambos puntos de monitoreo, arrojan cifras muy semejantes; convirtiéndolo en un método consistente.
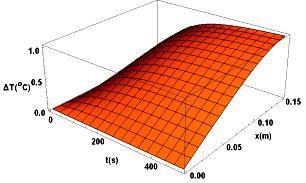
Figura 6. Gráfico de la variación de la temperatura en función del tiempo t y la coordenada x, en el compuesto: q = 0, 1 W; A = 4, 9 · 10-5 m2; L = 0, 15 m.
En la Figura 6 se aprecia el gráfico de la distribución de temperatura en función de la coordenada x y el tiempo t, según la ecuación 2, con los valores de χ y α efectivos obtenidos en la Tabla 2, q = 0, 1 W, A = 4, 9·10−5 m2, L = 0, 15 m. Nótese que, el aumento de temperatura continúa siendo pequeño (alrededor de un grado), sin embargo, mayor que en el caso de la barra de cobre homogénea. Esto se debe a que, al ser la conductividad térmica efectiva del compuesto menor a la del cobre, la velocidad de propagación del flujo de calor es menor; por lo tanto, se acumula más calor en los puntos monitoreados.
3.3. Implementación del método
Hasta aquí, se ha calculado numéricamente la conductividad y difusividad térmicas efectiva de un compuesto a base de cobre (65,7 %) – plomo (34,3 %). Si bien es necesario ampliar el número de simulaciones a otros tipos de configuraciones y, de ser posible, llevarlo a la práctica, se logra estimar bajo condiciones adecuadas los valores térmicos efectivos, que se encuentran en la Tabla 2.
En este sentido, se ha utilizado una herramienta informática SolidWorks®2016, cuyo método de cálculo de elementos finitos, está validado para la obtención de propiedades térmicas en un compuesto unidimensional, para las condiciones en que se diseñó la muestra [29]. Asimismo, los valores de la conductividad y difusividad térmicas efectivas obtenidas están dentro del intervalo que se establece en [30].
4. Conclusiones
La metodología numérica presentada en este trabajo se puede convertir en una herramienta para el cálculo de la conductividad y difusividad térmicas efectivas de un compuesto sólido unidimensional. Como ventaja, no se necesita, en general, conocer ni la geometría ni las dimensiones exactas del material insertado (aunque este debería estar disperso), tampoco las propiedades térmicas de los materiales constituyentes, pues solo se necesita monitorear la temperatura en varios puntos y ajustar los valores de χ y α a la ecuación 2.
