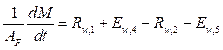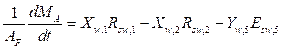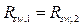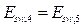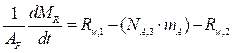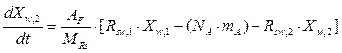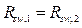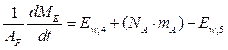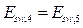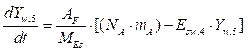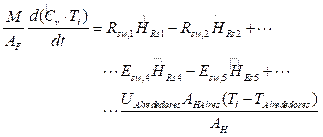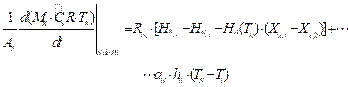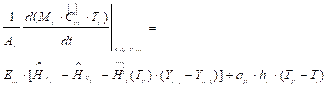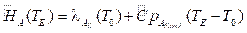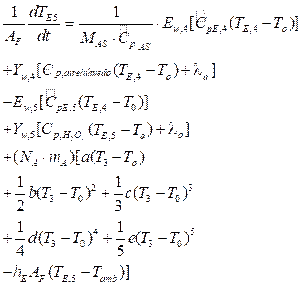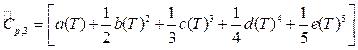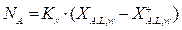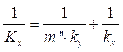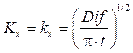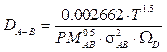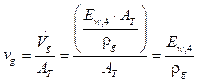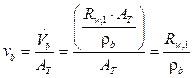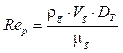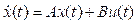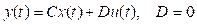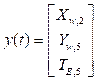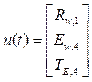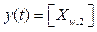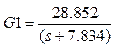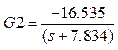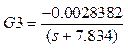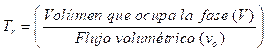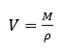Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
En el campo de la Ingeniería de Control, es de gran utilidad usar modelos matemáticos para representar los comportamientos que tienen los fenómenos de la naturaleza. Los modelos son abstracciones de una porción de la realidad que permiten dar explicación matemáticamente a lo que sea que esté sucediendo dentro de unas fronteras establecidas. Siendo los fenómenos de la naturaleza inherentemente dinámicos, la herramienta matemática empleada en la representación de dichos fenómenos tendrá que ser un conjunto de ecuaciones diferenciales que, acorde a las características del sistema que se desea modelar, se obtendrán de las diferentes leyes físicas que lo gobiernen. En nuestro caso especial, dado que se trata de un sistema con interacciones físico-químicas, serán las leyes de conservación de la masa y la energía.
Este artículo se desarrolló con el objetivo de realizar balances en estado dinámico para el proceso de secado de pasta cerámica. El modelo se realizó como un ejercicio académico para Colcerámica S.A.S., una de las unidades de negocio de la organización CORONA en Colombia. El equipo que se desea modelar es un secador spray. La motivación principal al desarrollar el modelo es la aplicación de estrategias de control a la variable humedad, la cual es de suma importancia para el proceso. Si bien en la actualidad existen sensores que miden la humedad de pasta cerámica en tiempo real, la empresa Colcerámica S.A.S no posee un sensor que realice dicha tarea y en este caso un modelo podría ofrecer la oportunidad de predecir la dinámica de la variable de interés en términos de variables que si se pueden medir.
En este caso se optó por no realizar identificación, ya que se quería obtener una descripción fenomenológica que diera a conocer el proceso de secado de pasta cerámica y además permitiera dar explicación al comportamiento de las dinámicas del proceso en el equipo. Adicionalmente, el ejercicio de representar el proceso a través de ecuaciones diferenciales obliga a conocer en profundidad el mismo. En otras palabras, conocer internamente el modelo, por lo que un modelo de tipo caja negra fue descartado. Se logró describir adecuadamente la fenomenología del equipo, consiguiendo predecir los cambios en la humedad a la salida, basados en las condiciones de entrada del mismo y acercándose suficientemente a los estados estacionarios del proceso real, resaltando que fueron usados datos de un equipo en operación.
En este documento se expondrá pues, la aplicación de la metodología de modelado expuesta en 1. Dado que dicha metodología plantea un modelado en estado dinámico, los resultados de esta permitieron hacer una predicción de las propiedades de la variable humedad.
Trabajos Relacionados
Existen diversos autores que han enfrentado ejercicios de modelado para secadores spray. La mayoría tratan procesos relacionados con alimentos como la producción de leche en polvo, colorantes naturales y frutas deshidratadas. Entre estos, se encuentran algunos que presentan balances en estado estacionario 2, 3, (4, pero también existen otros con balances en estado dinámico 5, 6, (7. En menor proporción encontramos al proceso cerámico, en el cual únicamente plantean los balances para los estados estacionarios 8. Los balances en estado estacionario suelen realizarse con el fin de conocer los puntos de operación de los equipos y la cantidad de materia prima requerida para obtener determinada cantidad de producto; mientras que los balances en estado dinámico son usados en la aplicación de estrategias de control y para representar (predecir) los cambios de alguna o varias propiedades.
Los autores, en general, expresan que la humedad es una variable de suma importancia para el proceso de secado, en términos de las propiedades de los productos. Particularmente, en el proceso industrial de la pasta cerámica, la granulometría es un parámetro que adquiere gran importancia en la etapa de prensado (seguida de la atomización). Es por esto que el control de humedad de las partículas al final de la atomización es crucial, pues si esta no es retirada adecuadamente (manera y cantidad), el grano final presentaría algunos problemas según los estándares de calidad 9, 10.
Metodología De Modelado
Paso 1: Descripción del proceso y diagrama de flujo
Según la metodología de modelado 1, se inicia con una descripción verbal del proceso, enunciando las características más importantes del mismo.
El equipo que se desea modelar es un secador Spray ATM-52, en el que se aplica una reducción del contenido de líquido de los productos desde un valor inicial hasta un valor final deseado, necesario para lograr que las cerámicas queden con las especificaciones de calidad requeridas en sus propiedades físicas. Existen diferentes factores que afectan el proceso de secado como la temperatura, velocidad del aire con el que se seca, el tipo de producto que se secará, etc. Esto da lugar a que en el mercado se desarrollen muchos secadores, las diferencias de éstos residen en la forma en que se mueven los sólidos a través de la zona de secado y en la forma en la que se transmite calor 11.
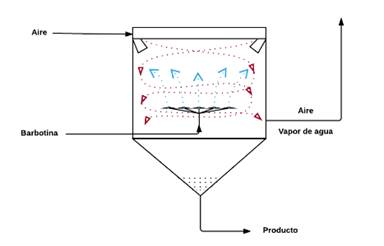
El Secador Spray ATM-52 es un equipo perteneciente al proceso inicial para la elaboración de cerámicas. En él se seca la Barbotina (una mezcla de minerales y arcillas de la que se obtiene la contextura cerámica). Esta mezcla es llevada al secador que se encarga de convertirla en gotitas a través de un Atomizador. Son las gotitas de la mezcla las que serán secadas a partir de una corriente de aire caliente. Esta corriente de aire forma un torbellino que garantiza valores de humedad y granulometría constantes a través del equipo (es decir, en las divisiones espaciales de éste), ahorrándose así tiempo y energía 12. Después de que se secan las gotitas, caen por gravedad a la corriente que extrae este producto mientras que la humedad retirada de la Barbotina sale por una corriente lateral de vapor de agua mezclado con aire.
En la Fig. 1 se muestra un diagrama del proceso.
Paso 2: nivel de detalle
El nivel de detalle está orientado a las preguntas que responden el modelo y las hipótesis con las cuales se comenzará a resolver el problema de modelado. Este a su vez se puede descomponer en los siguientes 4 ítems:
Objetivo del modelo:
El objetivo del modelo es determinar la variación de la humedad del flujo de producto en el tiempo. Es decir, se buscará un modelo dinámico con la cualidad de representar esta humedad para todo tiempo “t”.
Nivel de detalle del modelo:
En este caso, se abordará el problema desde un nivel macroscópico, suponiendo a las sustancias como nuestros sistemas de interés. Esto porque para efectos del modelo que se desea encontrar, es más conveniente trabajar como se describió con anterioridad. Además, el modelo se considera de parámetros concentrados: dependientes solo del tiempo y no del espacio.
Hipótesis de modelado:
Al equipo ingresan dos corrientes, (1): flujo de Barbotina o Refinado y (4): flujo de Aire o Extracto. La corriente (1), contiene gotitas de Barbotina provenientes del atomizador, que salen disparadas en sentido vertical para encontrarse con la corriente de aire. Una vez ingresan, las corrientes se encuentran en contra-corriente, pero poco después establecen su sentido como co-corriente ya que, al encontrarse con el flujo de aire, las gotitas toman su misma dirección, recordando que el aire se mueve en forma de torbellino dentro del equipo. Como el fenómeno de transferencia de masa se da en su mayoría cuando las corrientes se encuentran en co-corriente, posteriormente se hará la suposición de que dentro del equipo dichos flujos solo se encuentran en co-corriente, pues la situación en la que se encuentran en contra-corriente es despreciable desde la perspectiva del fenómeno de transferencia de masa. Una vez finalizada la transferencia, sale la corriente de producto por la corriente (2) y el aire cargado de la humedad extraída por la corriente (5).
Suposiciones:
Las suposiciones son cualidades que se asignarán al sistema con el objetivo de simplificar el modelado del mismo. Como lo que se desea realizar es un modelado enfocado únicamente en el comportamiento de la humedad, incluir aspectos que perturben el sistema podría dificultar el entendimiento inicial del comportamiento de la variable dentro del equipo, para evitar eso, se realizan las siguientes suposiciones que simplifican el sistema:
Agitación perfecta dentro del equipo (homogeneidad de las propiedades). Pues la corriente de aire caliente lleva una gran velocidad en forma de torbellino que permite una distribución homogénea de los componentes dentro del equipo. Además, esta suposición permite simplificar los balances de materia y conservar las propiedades de las gotitas de barbotina a lo largo del equipo.
La interacción de flujos entre la corriente de aire caliente y la barbotina es en co-corriente. La barbotina adquiere el mismo sentido de flujo del aire caliente en el instante en el que ambas fases se ponen en contacto, además como se menciona previamente, la situación en la que se encuentran en contra-corriente es despreciable desde la perspectiva del fenómeno de transferencia de masa.
El secador es adiabático, es decir, no hay intercambio energético de calor con los alrededores. Pues todas las paredes internas de la torre de secado están realizadas con chapas de acero inoxidable, térmicamente aisladas con lana de roca de alta densidad y grueso espesor 12.
Las gotitas de barbotina se consideran esféricas. Pues la geometría, la forma de distribución de las boquillas y la presión con la que la barbotina sale del equipo, pueden garantizar la esfericidad de las gotitas del refinado 12.
No hay incrustaciones dentro del equipo. A pesar de que las incrustaciones son muy comunes en este tipo de equipos, en Colcerámica S.A.S realizan una limpieza constante de la torre de secado, lo que permite realizar la suposición.
No hay arrastre de sólidos por parte de la corriente de aire y el vapor de agua, pues el equipo cuenta con tamices y filtros que evitan arrastre de sólidos en la corriente de aire.
El aire que ingresa al equipo es seco, es decir, está completamente insaturado. Dado que no se cuenta con el porcentaje exacto de humedad que satura el aire de entrada al equipo, la temperatura con la que ingresa es lo suficientemente alta (T=600°C) como para realizar esta consideración.
La cantidad de aire seco que ingresa y que sale del equipo, es la misma. Pues dentro del equipo no hay acumulación de aire reportada.
Paso 3: sistemas de proceso
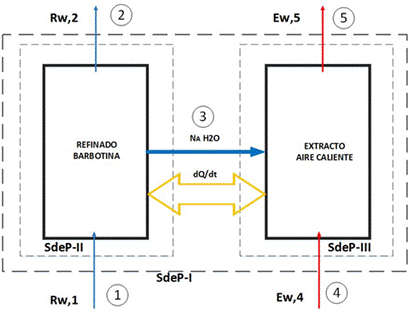
De acuerdo con el nivel de detalle descrito anteriormente, se muestran los sistemas de proceso seleccionados a través de un diagrama de bloques en el que se definen dos fases: Fase Refinado (R: Barbotina) que es aquella fase líquida que entrega el Soluto A. En este caso el Soluto A es el agua extraída de la Barbotina a partir de ahora llamada R. Esta fase será descrita como SdeP-II. Fase Extracto (E: Aire Caliente) que es aquella fase gaseosa que recibe el Soluto A (Agua) entregado por la Fase Refinado R. Esta fase será descrita como SdeP-III. Al conjunto de todo el sistema (sistema total) se describirá como SdeP-I. En la Fig. 2 se expone el diagrama de bloques que será utilizado para la realización de los Balances de Materia y Energía. Cabe resaltar que los sistemas de proceso descritos a continuación son supuestos como suficientes para conseguir el objetivo del modelo propuesto.
Paso 4: aplicar principios de conservación sobre cada uno de los sistemas de proceso
Cabe resaltar que estos balances se encuentran en base libre de soluto (agua), permitiendo dar cuenta de la cantidad exacta de soluto en cada fase 13, 14.
Balances de masa para el SdeP-I:
Balance de masa total
(1)
Balance de masa por componente. Soluto A: agua. Como en la corriente 4 no ingresa nada de agua, entonces Y w,4 = 0. Lo que reduce la expresión a:
(2)
Para el aire saturado, se deben realizar otros cálculos de propiedades tales como: humedad de saturación y humedad absoluta del aire de entrada.
Balance de masa por componente. Sólidos secos en el Refinado. Como en el proceso todo lo que entra de sólidos secos es igual a lo que sale, no hay acumulación y por lo tanto el término (1/A F )(dM RS /dt) = 0.
(3)
Balance de masa por componente. Aire seco en el Extracto. De nuevo, como todo lo que entra de aire seco al proceso es igual a lo que sale, no hay acumulación, por lo tanto el término (1/A F )(dM ES /dt) = 0.
(4)
Balances de masa para el SdeP-II:
Balance de masa total.
(5)
Como en la corriente 3 solo circula agua, se tiene que N A,3 = N A .
Balance de masa por componente: Soluto A, en nuestro caso es el agua que se transfiere de la barbotina al aire caliente.
(6)
Balance de masa por componente. Sólidos secos en el refinado. Note que (3) es igual a (7).
(7)
Balances de masa para el SdeP-III:
Balance de masa total.
(8)
Balance de masa por componente: Aire seco en Extracto. Note que (9) es igual a (4).
(9)
Balance de masa por componente: Soluto A. Teniendo en cuenta que la cantidad de aire seco es una constante, se tiene que:
(10)
Balances de energía:
El equipo es considerado adiabático, entonces la transferencia de energía térmica solo ocurre en el interior del cuerpo del secador, considerado como una cámara cilíndrica, entre el líquido y el aire caliente. A continuación, se muestran los balances de energía correspondientes 13, 14:
Balance de energía SdeP-I:
(11)
Balance de energía SdeP-II 13:
(12)
Balance de energía SdeP-III:
(13)
Como E es la fase más energética (pues contiene el calor de cambio de fase), calculamos la entalpía como sigue:
(14)
donde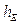 
es el coeficiente convectivo local de transferencia de calor.
Así las cosas, se tiene el balance de energía para la temperatura de salida del aire en el secador, clave para aplicar posteriormente el control 5:
(15)
donde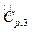 
es la capacidad calorífica de la corriente de transferencia de humedad 5.
(16)
dónde: a = 1.92964×101, b = 4.721180×10-1, c = -1.33878×10-3, d = 1.311424×10-6 y e = 4.30228×10-12.
La Tabla 1. presenta la descripción de cada una de los términos asociados a los balances de materia y energía.
Paso 5, 6 y 7: selección de ecuaciones dinámicas con información valiosa, variables, parámetros, constantes y ecuaciones constitutivas.
Las Ecuaciones Diferenciales de Balance esenciales son aquellas que contienen información valiosa para cumplir con el objetivo del modelo. Tenemos 14 ecuaciones dinámicas que nos dan la descripción del modelo, sin embargo, existen algunas ecuaciones redundantes y otras que no son de total utilidad. Por tanto, las EDB esenciales serán: (5), (6), (8), (10) y (15).
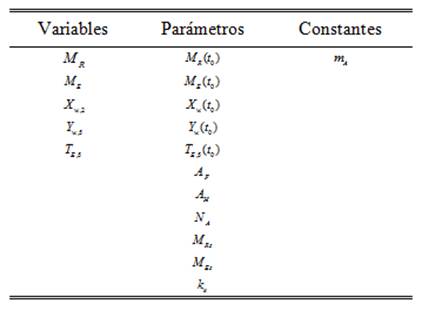
En la Tabla 2. se presentan variables, parámetros y constantes, además de las ecuaciones constitutivas.
Flux de Transferencia de Masa NA:
La ecuación constitutiva más importante que complementa los balances y es necesaria para resolver el modelo, es una que permita calcular el parámetro N A . Adicionalmente se tendrán en cuenta términos que permitan encontrar el área de transferencia de masa y también otras ecuaciones que se derivan de los balances de materia
(17)
En esta ecuación K
x
es el Coeficiente de transferencia local englobante de transferencia de masa con datos del líquido “x”, X
A,w
es la fracción de agua en el bulto y
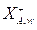es la fracción de agua en la concentración de equilibrio (humedad en el equilibrio). Estos coeficientes se representan a su vez, por coeficientes locales de transferencia de masa correspondientes a cada fase
(18)
Los coeficientes locales para cada fase k y y k x se hallan a partir de correlaciones. Sin embargo, se define el coeficiente local k x como el englobante (K x ), pues la fase que opone más resistencia a la transferencia de masa es la líquida. Por tanto, el coeficiente local k x será el coeficiente global K x . Así 15:
(19)
Dado lo anterior, las ecuaciones constitutivas vienen dadas por (17), (18), (19).
Término Difusividad
Se usará la Correlación de Chapman- Enskog para la difusividad en gases a baja presión.
(20)
donde T es la temperatura (K), D
A-B
es la difusividad en (cm2/s), p es la presión absoluta (bar), M
A
y M
B
son las masas moleculares de A y B (g/mol),
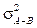es el diámetro característico de las moléculas (tomados de tablas) en
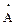y
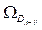es la integral de colisión para la difusión cuyo valor es tomado de tablas.
Velocidad del gas y velocidad de la gota:
Para calcular la velocidad del gas con la cual entra a la torre y para determinar la velocidad de la gota a la entrada del equipo se utiliza (22):
(21)
(22)
donde v
g
es la velocidad del gas, v
b
es la velocidad de barbotina a la entrada del equipo,
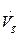es el flujo volumétrico del gas,
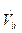es el flujo volumétrico barbotina y A
T
es el área transversal del equipo.
El cálculo de Reynolds se realiza mediante (23):
(23)
donde Re p es el número de Reynolds, D T el diámetro de la torre y μ g es la viscosidad del gas.
Verificación de los grados de libertad.
A continuación, se describen los grados de libertad para las ecuaciones de balance planteadas: Grados de Libertad = Ecuaciones - Incógnitas. Donde las incógnitas son: seis parámetros
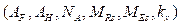, cinco variables dinámicas
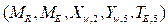, cinco condiciones iniciales de variables dinámicas
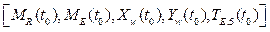. Y las ecuaciones son: cinco ecuaciones de balance: (5), (6), (8), (10), (15), dos ecuaciones constitutivas: (17), (19), nueve especificaciones operativas:
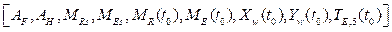y cero grados de libertad.
Como el número de ecuaciones planteadas es igual que el número de variables, el sistema si tiene solución.
PASO 9: Solución del modelo - resultados
Si bien se dispone de cinco ecuaciones de balance, dadas las condiciones del equipo real, se decide suponer las masas del refinado y del extracto como constantes. De esta manera, nos quedan solo las ecuaciones (6), (10) y (15). El modelo en variables de estado queda entonces descrito como:
(24)
(25)
Variables de estado:
(26)
Entradas:
(27)
Salidas:
(28)
Las matrices A, B y C no se describen de manera explícita, ya que se conocen las ecuaciones diferenciales y se definen los vectores x (t), u (t) y y (t). Estas pueden ser fácilmente calculadas.
La solución del modelo matemático del proceso generalmente es numérica dada la presencia de Ecuaciones Diferenciales no Lineales. Para tal fin se seleccionaron Matlab® y Simulink como plataformas para la solución del modelo presentado anteriormente. Para darle solución al modelo fue necesario hallar los parámetros de las ecuaciones constitutivas del paso 7.
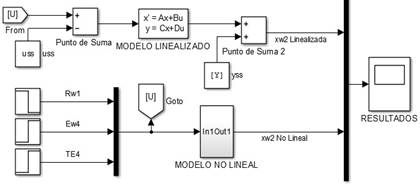
En la Tabla 3. se muestran los resultados obtenidos luego de la estimación de parámetros. Adicionalmente, en la Fig. 3 se presenta la estructura que se usó para la comparación de los modelos lineal y no lineal en Simulink.
Se puede apreciar el uso de un subsistema donde se define el modelo No Lineal como una función de Matlab® donde se encuentran las ecuaciones dinámicas. La función adicionalmente recibe los valores de las entradas y posteriormente, a través de una integración con un método numérico (ode45 en Matlab), ofrece el valor de la salida de interés. En nuestro caso, la Humedad. Para efectos comparativos, se usó la representación lineal en variables de estado junto con los valores en el punto de operación. El resultado de la comparación puede verse descrito en la Fig 4.
Funciones de transferencia
Al modelo no lineal, se le aplicó una linealización jacobiana con miras a obtener una representación lineal que permita un posterior diseño de controladores lineales. Luego de obtener dicha representación, se usa el comando “ss2tf” de Matlab® que permitió obtener las siguientes funciones de transferencia, a partir del modelo en variables de estado lineal.
Función de transferencia de la humedad en la corriente de refinado a la salida VS. Flux másico de la corriente de refinado a la entrada:
(29)
Según la ganancia que se evidencia, esta función de transferencia tiene sentido pues en la medida que la corriente de barbotina a la entrada aumenta, manteniendo las otras condiciones constantes, la humedad a la salida de esta corriente, debe aumentar.
Función de transferencia de la humedad en la corriente de refinado a la salida VS. Flux másico de la corriente del extracto a la entrada:
(30)
Según la ganancia que se evidencia, esta función de transferencia tiene sentido pues en la medida que la corriente de extracto a la entrada aumenta, manteniendo las otras condiciones constantes, la humedad a la salida de la corriente de refinado, debe disminuir.
Función de transferencia de la humedad en la corriente de refinado a la salida VS. La temperatura de entrada de la corriente de extracto a la entrada:
(31)
Según la ganancia que se evidencia, esta función de transferencia tiene sentido pues en la medida que la temperatura de la corriente del extracto a la entrada aumenta, manteniendo las otras condiciones constantes, la humedad a la salida de la corriente de refinado, debe disminuir.
Gráfica de Resultados del Modelo Lineal y No Lineal
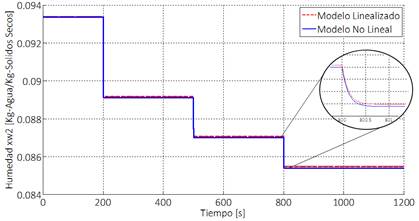
En la Fig. 4 se presentan los resultados de la comparación de los modelos lineal y no lineal ante cambios en los valores de las entradas. Se puede apreciar que al disminuir la corriente del refinado en la entrada un 1% en t =200s y aumentar tanto la corriente de extracto un 1% en t = 500s como la temperatura de entrada del aire un 0.5% en t=800s, la humedad disminuye. Se nota que el tiempo de estabilización de la humedad a la salida es pequeño. Para determinar el orden de dicho tiempo, se deben tener en cuenta los tiempos de residencia de las fases presentes, en el equipo (gas 28s y líquido 1.87s).
Estos tiempos de residencia nos aproximan a un tiempo de estabilización cercano al obtenido en el modelo, puesto que el aire entra al equipo en gran cantidad y el tiempo que esta fase permanece en el equipo es muy corto, ocasionando que la respuesta de la humedad a la salida sea rápida, lo cual se demuestra con el segundo tiempo de residencia obtenido (1.87s). Cabe resaltar que estos tiempos de respuesta dependen siempre de la capacidad del equipo que se use y de los flujos que se le alimenten.
Método de cálculo
El tiempo de residencia se define como:
(32)
(33)
Para la fase gas se asume que el aire llena toda la cámara (sección cilíndrica) por tanto, el volumen ocupado por la fase será el volumen de un cilindro. Para V ocupado fase = 383.147 m3, v o = 41865 m3/h, T r = 28s.
Para la fase líquida (Barbotina) se decide trabajar con una masa constante de 10 kg, con la que se calculó el punto de operación en la simulación propuesta, y con esta se obtuvo el volumen ocupado por la fase en el equipo y así el tiempo de residencia de ésta en el secador. Para v o = 11 m3/h, V ocupado fase = 0.00573 m3 según (33) por lo que T r = 1.87s.
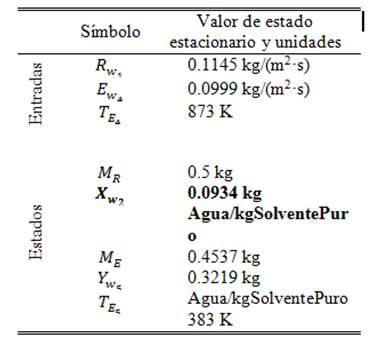
Resultados en estado estacionario
De los resultados consignados en la Tabla 4., se resalta que para las entradas fueron asumidos los valores reales de un equipo de secado ATM-52 en operación. Además, la humedad a la salida de este equipo tiene un valor ideal de 6.4 ± 0.4% (ya controlada) y considerando que el valor obtenido por el modelo a lazo abierto fue de 8.5%, ambos en base húmeda, se entiende que este modelo representa lo suficientemente bien el fenómeno tratado y verifica los valores de estado estacionario del proceso real, por lo que se muestra como un firme candidato para la aplicación de estrategias de control sobre esta variable.
Discusión
Los resultados encontrados comprueban que se logró describir adecuadamente la fenomenología del equipo, consiguiendo predecir los cambios en la humedad a la salida, basados en las condiciones de entrada del mismo y además acercarse bastante bien a los estados estacionarios del equipo y su tiempo teórico de estabilización. También dan cuenta de un buen ejercicio de modelado y linealización, ambos acordes con los comportamientos del equipo real. Se destaca la importancia de la inclusión de ecuaciones constitutivas, las cuales son una pieza fundamental que facilita la consecución del modelo. Se recomienda que el paso a seguir con este modelo sea la verificación del mismo y el diseño de estrategias de control para el equipo de secado.
