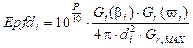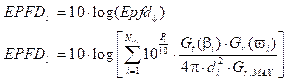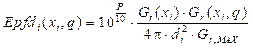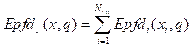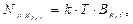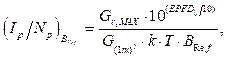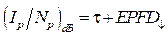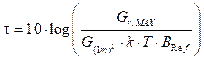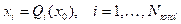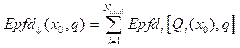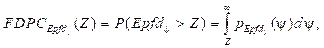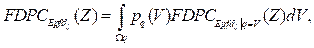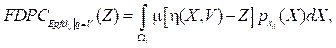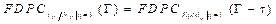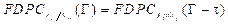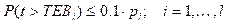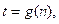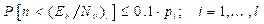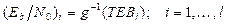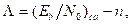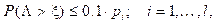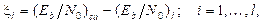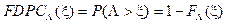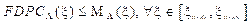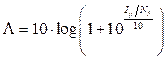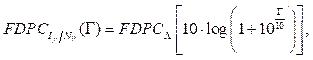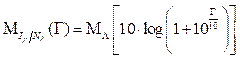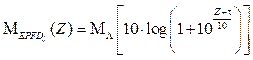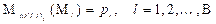Introducción
En décadas atrás, los sistemas de comunicaciones por satélites utilizaban específicamente satélites geoestacionario (GSO, Geostationary Orbit) para brindar servicios terrestres. La principal organización reguladora de los servicios de telecomunicaciones, Unión Internacional de Telecomunicaciones (ITU, International Telecommunication Union) en el artículo 22 del reglamento de radiocomunicaciones 1 establece los límites máximos para la densidad de flujo de potencia ocasionada en la superficie de la tierra por satélites GSO, de forma de garantizar la protección de los servicios fijos por satélites (FSS, Fixed Service Satellite). En el artículo 22 no es considerado la protección FSS contra interferencias generadas por los sistemas no-gestacionarios (N-GSO, Non- Geostationary Orbit).
A finales de los años 90, con el propósito de proteger estos sistemas frente a las interferencias generadas por los sistemas de satélites N-GSO se realizó la Conferencia Mundial de Radio-Comunicaciones (WRC-97, World Radiocommunication Conference) 2, donde se recomendó el estudio para la asignación de los límites de potencia que estos tipos de satélites deben tener para garantizar la protección de los sistemas fijos. Años después fueron realizados estudios y análisis sobre diferentes sistemas de constelación N-GSO que son descritos en 3, (4, (5, (6, (7, donde las interferencias generadas por los satélites N-GSO fueron obtenidas por medio de simulaciones.
Producto del desarrollo tecnológico de los últimos tiempos, donde los requerimientos de los sistemas de comunicaciones en término de ancho de banda son más exigentes, la ampliación de las bandas de frecuencias que pueden ser utilizadas por los sistemas de comunicaciones por satélites N-GSO fue aprobada mediante la Resolución 127 8 en la (WRC-15), por lo que es necesario el estudio de las técnicas y operacionales que envuelven estos sistemas satelitales al operar en estas nuevas bandas de frecuencias. Fue observado en el artículo 22 que los límites de potencias para las bandas de 3.7- 4.2 GHz fueron tratados solo para sistemas de satélites de órbita elípticas (HEO, Highly Elliptical Orbit).
En este sentido, el estudio de los límites de potencias para sistemas N-GSO es un tema importante en el desarrollo de los sistemas satelitales. Por tanto, el objetivo de esta investigación es realizar un análisis de los límites de la densidad de flujo de potencia equivalente para la protección de estaciones terrenas del servicio fijo por satélites en la región de Norte América.
La presente investigación tiene la siguiente estructura: la Sección II, revisa los modelos matemáticos de densidad de flujo de potencia, relacionamiento entre densidad de flujo y relación entre la razón potencia interferente, y potencia de ruido y determinación de la Función Distribución de Probabilidad Complementaria. La Sección III proporciona el desenvolvimiento para la obtención de los límites de la densidad de flujo de potencia equivalente en el enlace descendente. Los resultados de las simulaciones se presentan en la Sección IV para examinar y analizar el cumplimiento de la máscara dados dos sistemas de satélites N-GSO. La Sección V es concluida la investigación
Modelo Matemático
Densidad de Flujo de Potencia equivalente en el enlace descendente
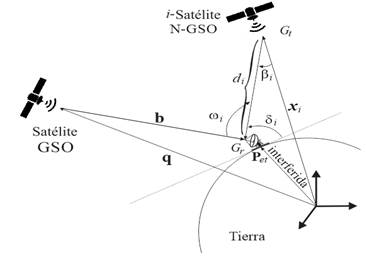
La Fig 1. muestra el i-ésimo satélite de una constelación N-GSO, que está localizado en la posición x i y la interferencia producida sobre una estación terrena receptora posicionada en P et , donde su antena receptora apunta en la dirección del satélite GSO y es caracterizada por el vector b.
En la Fig. 1, β i representa el ángulo entre el apuntamiento de la antena transmisora del satélite interferente y la dirección de la estación terrena interferida. El ángulos δ i representa, el ángulo de llegada de la señal interferente y ω i es el ángulo entre el apuntamiento de la antena receptora de la estación terrena interferida y la dirección del satélite N-GSO interferente. Una vez descritos los términos de la Fig. 1, es posible expresar en (1) la densidad de flujo de potencia ocasionada por el i-ésimo satélite de la constelación N-GSO en la estación terrena interferida.
La densidad de flujo de potencia equivalente en el enlace descendente EPFD ↓ y Epfd ↓ expresadas en dB(W/m2) y W/m2, respectivamente, y generadas por todos los satélites visibles (N vis ) de la constelación del sistema N-GSO sobre la estación terrestre interferida, son dadas por la siguiente ecuación:
En la Fig 1. ilustra que existe una dependencia de los ángulos β i y ω i con los vectores x i , P et y q. Considerándose, que la posición de la estación terrena interferida es fija y conocida, y al asumir que todos los satélites de la órbita no geoestacionaria trabajan con la misma potencia. De este modo la expresión (1) puede ser reescrita como en (3).
La densidad Epfd ↓ es posible expresarla como (4) al utilizar las consideraciones mencionadas anteriormente.
Relacionamiento entre EPFD ↓ y I p /N p (razón entre la potencia interferente y la potencia del ruido)
Un parámetro que es necesario analizar para evaluar el nivel de densidad de flujo de potencia equivalente es I p /N p que representa la razón entre las potencias interferentes y el ruido en la banda de referencia B Ref .
La EPFD ↓ expresada en dB(W/m2) se relaciona con la potencia de interferencia en la banda de referencia mediante el área efectiva de la antena de la estación terrestre receptora del sistema de satélite GSO. El área efectiva es determinada a partir del cociente entre G r,MAX y G (1m) 2, que representa la ganancia de un metro cuadrado, la cual depende de la longitud de onda λ asociada a la frecuencia central de las señales que intervienen.
La temperatura T del ruido en el receptor de la estación del sistema satelital GSO y la potencia del ruido térmico del receptor en la banda B Ref (ancho de banda) está relacionada por la constante de Boltzman (k) y se expresa en (5),
al emplear el desenvolvimiento matemático descrito en 9, es posible obtener una expresión que relaciona EPFD ↓ y I p /N p , dado por:
la expresión (7) representa el relacionamiento entre la potencia interferente y el ruido en la banda de referencia en dB.
El relacionamiento descrito anteriormente, las operadoras de sistemas satelitales se sienten más confortables para determinar los valores de Ip/Np que se relaciona con la densidad de flujo de potencia equivalente.
Determinación de la Función Distribución de Probabilidad Complementaria de EPFD ↓
Las posiciones orbitales x i , i = 1,…, N total , donde N total representa el número total de satélites en la órbita N-GSO y la posición orbital q del satélite GSO son caracterizadas como vectores aleatorios. Debido a este modelaje la Epfd ↓ es también caracterizada como una variable aleatoria.
En la presente investigación son considerados sistemas de satélites N-GSO que presentan las características de la constelación de Walker Delta 10. En estas constelaciones, si la posición de un satélite (satélite de referencia) es conocida, es posible determinar las posiciones de los restantes satélites que conforman la constelación. Donde x 0 es la posición del satélite de referencia puede ser definida la expresión (9), con Q i (x 0), i = 1,…, N total definida por la estructura de la constelación en 10
Al tener en cuenta la ecuación anterior, es posible expresar (4) como:
En la expresión (10) los vectores aleatorios x 0 y q influyen en la densidad de flujo de potencia equivalente en el enlace de bajada, en la banda de referencia B Ref , ocasionadas por todos los satélites que son visibles en la constelación de satélites N-GSO: por tal razón, la Epfd ↓ es modelada como una variable aleatoria donde su función distribución de probabilidad complementar es dada por:
en (11)p Epfd↓ (ψ) representa la función densidad de probabilidad de la variable aleatoria Epfd ↓ y puede ser escrita a partir de la función de probabilidad conjunta de las variables aleatorias Epfd ↓, x 0 y q. Consecuentemente, la FDPC Epfd↓ (Z) es posible escribirla como:
donde Ω q es el espacio donde q toman valores y FDPC Epfd|↓q=V (Z) representa la función distribución de probabilidad complementaria condicional de la variable aleatoria Epfd ↓ que puede ser escrita como (13) al utilizar el desarrollo matemático descrito en 9,
con u (⁎) como la función degrau unitario, η (X, V) es determinada por las expresiones (3) y (4) y p x0 (X) es la función densidad de probabilidad del satélite referente, cuya expresión es determinada por el método analítico descrito en11.
La función distribución de probabilidad complementaria de la variable aleatoria I p /N p puede ser determinada mediante la expresión (7) y (13). Luego se tienen como resultado las siguientes expresiones:
donde τ es determinada mediante (8).
Límites de EPFD ↓
La recomendación ITU-R S.1323 12, establece que, en una determinada red de satélites, la interferencia generada por las emisiones de otras redes de satélites que trabajan en la misma banda de frecuencia, deben ser responsables, a lo sumo por el 10 % del tiempo permitido para las tasas de error de bit (TEB) descritas en las condiciones de desempeño de la red considerada. Esto indica que las variaciones de TEB causadas únicamente por la influencia de interferencias externas deben cumplir las condiciones impuestas en la siguiente ecuación:
Observe que la relación de las tasas de error de bit (TEB) con la razón energía de bit y nivel de ruido térmico (E b /N 0) es dada por la siguiente función:
donde t es la tasa de error de bit y n es la relación energía de bit/nivel de ruido térmico. Una disminución de la razón E b /N 0 resulta en un aumento de la TEB, por lo que la función g es decreciente. Como resultado, las restricciones en (16) pueden ser también reescritas de la siguiente forma:
Al considerar solo la presencia de las interferencias generadas por fuentes externas, sea Λ la degradación, es posible expresar la relación E b /N 0 en cielo abierto ca (clear sky) en dB:
donde (E b /N 0) ca representa la razón E b /N 0 en cielo abierto.
Al considerar la expresión (20) las restricciones de (18) pueden ser expresadas como,
en la expresión anterior el término ξ i se determina como:
En la expresión (21) es posible observar que las restricciones muestran que la Función Distribución de Probabilidad Complementarias de la degradación Λ proveniente de las interferencias externas se expresa por la siguiente ecuación,
Las restricciones de la expresión (23) pueden ser cumplidas para muchas curvas. Al emplear 13, donde se muestra una serie de pasos que conforman una metodología que, al considerar los valores mínimos ξ min y máximos ξ max de la variable aleatoria Λ es posible determinar, a través de una parametrización adecuada y de la solución de un problema de optimización con algunas restricciones convenientes, una función densidad de probabilidad para la variable aleatoria Λ, tal que la probabilidad de Λ que pertenezca al intervalo abierto (ξ min , ξ max ) sea el máximo.
Se propone que la función distribución de probabilidad complementaria asociada a la función densidad de probabilidad obtenida sea empleada como una máscara ΜΛ (ξ) para analizar el comportamiento estadístico de la degradación Λ derivada de las interferencias externas que afectan el enlace de un receptor de una estación terrestre. Por tanto, el comportamiento estadístico de la variable aleatoria Λ debe satisfacer la siguiente condición,
La degradación de la variable aleatoria Λ de la razón E b /N 0, provocada por la interferencia externa, se relaciona con la razón interferencia-ruido como en (9) y puede ser expresada en dB:
donde I p /N p representa la razón interferencia-ruido expresada en dB. Al emplear el relacionamiento de (25) puede mostrase que,
que indica que la función distribución de probabilidad complementaria de la razón interferencia-ruido puede ser obtenida directamente de la función distribución de probabilidad complementaria de la variable aleatoria Λ. Luego dado el relacionamiento considerado en (24) es posible mostrar que:
Al considerar las expresiones (27) y (15) puede ser obtenida una máscara de EPFD ↓
La Tabla 1. destaca los parámetros utilizados en conjunto con la metodología desarrollada en 13 y el relacionamiento obtenido en (27) para determinar la máscara Μ EPFD↓ (Z). Además, son considerados ξ min = 0, ξ max = 25 y ℕ = 3. Los límites de EPFD ↓ correspondientes a los parámetros anteriormente relacionados son mostrados en la Tabla 2, válidos para diámetro de antenas 1.8 metros, que corresponden a las muestras de la máscara Μ EPFD↓ , o puede ser traducido como los valores que del par (Μ l , p l ), con l definido (1,2,…,B), donde debe ser satisfecha la siguiente relación
Tabla 1 Parámetros Empleados en la Obtención de Μ EPFD (Z)
| TEB i | (E b /N o ) i [dB] | ξ i [dB] | p i |
|---|---|---|---|
| 1×10-6 | 6.5 | 10.3 | 0.0004 |
| 1×10-8 | 7.6 | 11.4 | 0.006 |
| 1×10-9 | 8.7 | 12.5 | 0.004 |
Resultados y Discusión
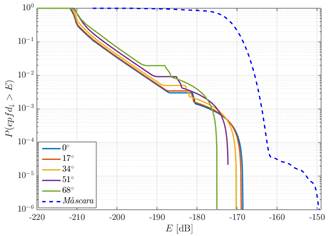
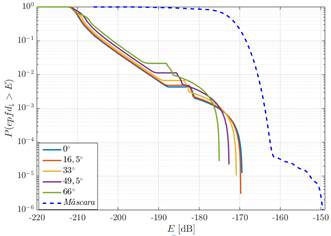
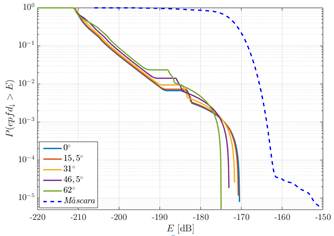
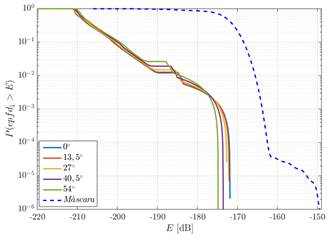
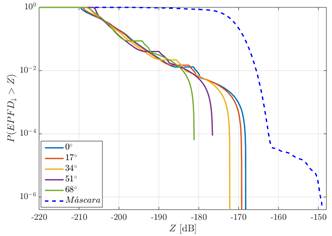
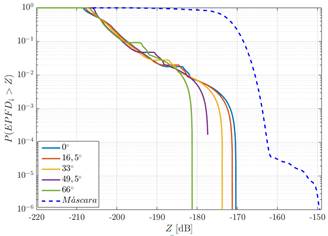
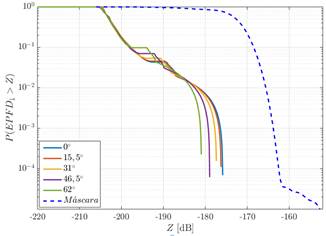
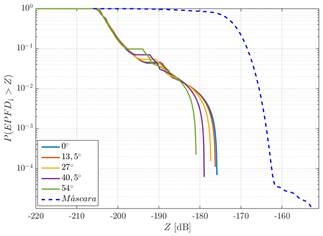
En esta sección se presentan los resultados de las simulaciones de la investigación. Para realizar el análisis del cumplimiento de los límites de la función distribución de probabilidad complementaria de la densidad de flujo de potencia equivalente para los servicios fijos por satélites que satisfacen la máscara de la Fig 2. en la región de Norte América, fueron empleados dos constelaciones de satélites N-GSO de tipo Walker Delta cuyas características son presentadas en la Tabla 3.
Tabla 3 Características Técnicas de los Sistemas de Satélites N-GSO Considerados
| Sistema | B | D |
| Altura [km] | 1414 | 1375 |
| Inclinación del plano orbital [grado] | 55 | 84,7 |
| Número de planos orbitales | 4 | 12 |
| Número de Satélites por planos | 5 | 24 |
| ∆ℳ entre planos adyacentes [grados] | 0 | 1,25 |
| Espacio entre planos [grados] | 90 | 15,36 |
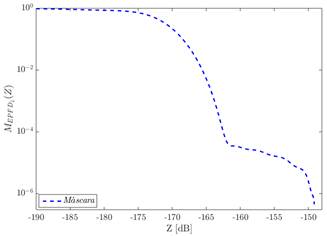
Fig 2 Máscara a ser satisfecha por la función distribución de probabilidad complementaria de la densidad de flujo de potencia equivalente.
En los dos escenarios analizados, se consideraron una frecuencia de 4 GHz, los diagramas de radiación propuestos en 1 y la recomendación dada en 14, para las antenas de la estación terrena interferida y de los satélites N-GSO de la constelación, respectivamente. Para los sistemas descritos en la Tabla 3. fueron definidas estaciones terrenas interferidas ubicadas en las siguientes latitudes: 30, 38, 46 y 55 grados. Los resultados obtenidos para las diferentes latitudes de la estación terrena interferida son comparados con la máscara de la Fig 2. Estas comparaciones son presentadas en las siguientes figuras
Conclusiones
En esta investigación se ha presentado y discutido el desenvolvimiento matemático para la determinación de la máscara EPFD↓ al partir de criterios para la protección del Sistema Fijo por Satélites ya establecidos. Fue descrita una metodología para determinar una máscara EPFD↓, esta máscara fue avalada a través de comparaciones con las funciones distribución de probabilidad complementaria de las densidades de flujo de potencia equivalente generadas por los enlaces descendentes de un sistema de satélites non-GSO en la estación terrestre receptora interferida GEO al emplear una antena receptora de 1.8 metros. En la comparación fueron analizados dos sistemas de satélites non-GSO con estructura de la constelación de Walker Delta 10. Dada la investigación realizada se concluye que la máscara de protección obtenida es adecuada para proteger estaciones terrenas interferidas en la región de Norte América de la interferencia generada por los sistemas de satélites N-GSO analizados en este trabajo.